Тело Кеплера — Пуансо

Тело Кеплера — Пуансо — тело, представляющее собой правильный звёздчатый многогранник, не являющийся соединением платоновых и звёздчатых тел.
В 1811 году французский математик Огюстен Коши установил, что существуют всего 4 правильных звёздчатых тела, которые не являются соединениями платоновых и звёздчатых тел[1]. К ним относятся описанные в 1619 году Иоганном Кеплером малый звёздчатый додекаэдр и большой звёздчатый додекаэдр, а также большой додекаэдр и большой икосаэдр, открытые в 1809 году Луи Пуансо[2]. Остальные правильные звёздчатые многогранники являются или соединениями платоновых тел, или соединениями тел Кеплера — Пуансо[3].
История[править | править код]

Некоторые из многогранников Кеплера — Пуансо в той или иной форме были известны ещё до Кеплера[4]. Так, изображение малого звёздчатого додекаэдра присутствует в мраморной мозаике, украшающей пол собора Святого Марка в Венеции. Эта мозаика датируется XV веком, авторство иногда приписывается Паоло Уччелло. В XVI веке немецкий ювелир Венцель Ямницер в своём труде Perspectiva corporum regularium (рус. Перспективы правильных тел) изображает большой додекаэдр и большой звёздчатый додекаэдр[5]. По-видимому, до Кеплера никто из художников и учёных не знал всех свойств этих тел.
Малый и большой звёздчатые додекаэдры, которые иногда именуют «многогранники Кеплера», впервые были полностью описаны в трактате Иоганна Кеплера 1619 года Harmonices Mundi[6]. Каждое из этих тел имеет центральную выпуклую область каждой грани, «скрытую» внутри, при этом видны только треугольные плоскости. Кеплер описывает многогранники, используя ту же модель, с помощью которой Платон в диалоге Тимей описывает построение правильных многогранников на основе правильных треугольников[7]. Последним шагом Кеплера было признание, что эти многогранники являются правильными, даже если они не являются выпуклыми, в отличие от обычных платоновых тел.
В 1809 году Луи Пуансо вновь исследовал многогранники Кеплера и обнаружил ещё два правильных звёздчатых многогранника — большой икосаэдр и большой додекаэдр[2]. При этом Пуансо не был уверен, что выявил все возможные виды правильных звездчатых многогранников. Но в 1811 году Огюстен Луи Коши доказал, что существуют всего 4 правильных звёздчатых тела, которые не являются соединениями платоновых и звёздчатых тел, а в 1858 году, Жозеф Бертран представил более общее доказательство[4]. В 1859 году Артур Кэли дал многогранникам Кеплера — Пуансо названия, под которыми они, как правило, известны сегодня[4]. Сто лет спустя Джон Конвей разработал терминологию для звёздчатых многоугольников. В рамках этой терминологии он предложил слегка изменённые имена для двух из правильных звёздчатых многогранников[8].
| Терминология Кэли | Терминология Конвея |
| Малый звёздчатый додекаэдр | Звёздчатый додекаэдр |
| Большой додекаэдр | Большой додекаэдр |
| Большой звёздчатый додекаэдр | Звёздчатый большой додекаэдр |
| Большой икосаэдр | Большой икосаэдр |
Терминология Конвея в настоящее время используется, но не имеет широкого распространения.
Характеристики[править | править код]
Невыпуклость[править | править код]
Эти тела имеют плоскости в виде пятиугольников. Малый и большой звёздчатый додекаэдры имеют плоскости в виде невыпуклых правильных звёзд. Большой додекаэдр и большой икосаэдр имеют выпуклые плоскости[9][10].
У всех этих тел две плоскости могут пересекаться, образуя линию, которая не является ребром какой-либо плоскости, и, таким образом, часть каждой грани проходит через внутреннюю часть тела. Такие линии пересечения иногда называются ложными рёбрами. Аналогично, в случае, когда три таких линии пересекаются в точке, не принадлежащей углу какой-либо плоскости, эти точки называются ложными вершинами. Например, малый звездчатый додекаэдр имеет 12 пятиугольных граней с центральной пятиугольной частью, скрытой внутри тела. Видимые части каждой грани состоят из пяти равнобедренных треугольников, которые касаются грани в пяти точках. Можно рассмотреть эти треугольники как 60 отдельных плоскостей, образующих новый, неправильный многогранник, который внешне выглядит идентичным изначальному. Каждое ребро теперь будет разделено на три коротких ребра (двух разных видов), при этом 20 ложных вершин станут истинными, и, таким образом, в общей сложности у тела будет 32 вершины (опять-таки двух видов). Скрытые внутренние пятиугольники больше не будут являться часть многогранной поверхности, и могут исчезнуть. Теперь Эйлерова характеристика содержит: 60 — 90 + 32 = 2. Но этот новый многогранник уже не описывается символом Шлефли {5/2, 5} , и поэтому не является телом Кеплера — Пуансо, хотя по-прежнему выглядит, как одно из них[10].
Эйлерова характеристика χ[править | править код]
Тела Кеплера — Пуансо покрывают площадь описанных вокруг них сфер более одного раза, при этом центры граней выступают в качестве точек перегиба на поверхностях, имеющих пятиугольные плоскости, и вершин — на других поверхностях. Из-за этого тела Кеплера — Пуансо не обязательно топологически эквивалентны сфере, в отличие от платоновых тел, и, в частности, Эйлерова характеристика
для них не всегда имеет место. Шлефли установил, что все многогранники должны иметь χ = 2, и счёл, что малый звездчатый додекаэдр и большой додекаэдр не являются правильными многогранниками[11]. Эта точка зрения не была широко распространённой.
Модифицированная форма формулы Эйлера, выведенная Артуром Кэли[4], справедливая как для выпуклых многогранников, так и для тел Кеплера — Пуансо, выглядит так:
- .
Двойственность[править | править код]
Тела Кеплера — Пуансо существуют в двойственных (дуальных) парах[12]:
Сводная таблица свойств[править | править код]
Свойства тел Кеплера-Пуансо представлены в следующей таблице[13]:
| Название | Изображение | Сферическая проекция | Диаграмма звёздчатого многогранника |
Символ Шлефли {p, q} |
Поверхности {p} |
Ребра | Вершины | χ | Плотность | Группы симметрии | Двойственный многогранник |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Малый звёздчатый додекаэдр |

|

|

|
{5/2,5} | 12 {5/2} |
30 | 12 {5} |
-6 | 3 | Ih | Большой додекаэдр |
| Большой додекаэдр |

|

|

|
{5,5/2} | 12 {5} |
30 | 12 {5/2} |
-6 | 3 | Ih | Малый звёздчатый додекаэдр |
| Большой звездчатый додекаэдр |

|

|

|
{5/2,3} | 12 {5/2} |
30 | 20 {3} |
2 | 7 | Ih | Большой икосаэдр |
| Большой икосаэдр |

|
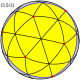
|

|
{3,5/2} | 20 {3} |
30 | 12 {5/2} |
2 | 7 | Ih | Большой звездчатый додекаэдр |
Отношения между правильными многогранниками[править | править код]
| Имеют одно и то же расположение вершин: | Имеют одни и те же вершины и рёбра: |
|---|---|
    Икосаэдр, Малый звёздчатый додекаэдр, Большой икосаэдр и Большой додекаэдр. |
  Малый звёздчатый додекаэдр и Большой икосаэдр. |
  Додекаэдр и Большой звёздчатый додекаэдр. |
  Икосаэдр и Большой додекаэдр. |
Малый звёздчатый додекаэдр и большой икосаэдр имеют одни и те же вершины и ребра. Икосаэдр и большой додекаэдр также имеют одни и те же вершины и ребра.
Все три додекаэдра являются звёздчатыми правильными выпуклыми додекаэдрами, большой икосаэдр является звёздчатым правильным выпуклым икосаэдром[14].
Если при пересечении фигур возникают новые рёбра и вершины, полученные многогранники не будут правильными, но их ещё можно считать звёздчатыми.
В массовой культуре и искусстве[править | править код]

В XX веке известный представитель имп-арта Мауриц Эшер в своём творчестве нередко обращался к сюжетам, основанным на восприятии различных многомерных фигур; в частности, его литография Гравитация изображает малый звёздчатый додекаэдр[15].
В основу перестановочной головоломки 1980-х годов — звезды Александера — положен большой додекаэдр[16].
См. также[править | править код]
Примечания[править | править код]
- ↑ Cauchy, 1813, pp. 68-86.
- ↑ 1 2 Poinsot, 1810, pp. 16-48.
- ↑ Wenninger, 1983, p. 46.
- ↑ 1 2 3 4 Stellation and facetting — a brief history. Дата обращения: 10 мая 2014. Архивировано 4 марта 2016 года.
- ↑ Jamnitzer-Galerie a. Дата обращения: 10 мая 2014. Архивировано 13 октября 2016 года.
- ↑ Harmonices mundi. Дата обращения: 22 ноября 2015. Архивировано 22 октября 2020 года.
- ↑ Field, 1984, pp. 207-219.
- ↑ Conway, Burgiel, Goodman-Strauss, 2008, pp. 404-408.
- ↑ Great Dodecahedron. Дата обращения: 30 ноября 2015. Архивировано 10 марта 2021 года.
- ↑ 1 2 Small Stellated Dodecahedron. Дата обращения: 30 ноября 2015. Архивировано 4 февраля 2021 года.
- ↑ Schläfli, 1901.
- ↑ Dual Polyhedron. Дата обращения: 30 ноября 2015. Архивировано 30 октября 2020 года.
- ↑ Kepler-Poinsot Solid. Дата обращения: 30 ноября 2015. Архивировано 21 января 2021 года.
- ↑ Great Icosahedron. Дата обращения: 30 ноября 2015. Архивировано 11 ноября 2020 года.
- ↑ Эшер, 2009.
- ↑ Alexander’s Star. Дата обращения: 22 ноября 2015. Архивировано 5 марта 2021 года.
Литература[править | править код]
- М. Веннинджер Модели многогранников. — М.: Мир, 1974. — 236 с.
- Эшер М.К. Графика. — М.: Арт-Родник, Taschen, 2009. — 96 с. — ISBN 978-5-404-00053-5.
- J. Bertrand. Note sur la théorie des polyèdres réguliers. — 1858. — Vol. 46. — P. 79-82, 117.
- Augustin Louis Cauchy. Recherches sur les polyèdres. — J. de l'École Polytechnique 9. — 1813. — P. 68-86.
- Arthur Cayley. On Poinsot’s Four New Regular Solids. — Philos. Mag.. — 1859. — Vol. 17. — P. 123—127 и 209.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss. Chapter 24, Regular Star-polytopes // The Symmetry of Things. — 2008. — P. 404—408. — ISBN 978-1-56881-220-5.
- H.S.M. Coxeter. (Paper 1), The Nine Regular Solids [Proc. Can. Math. Congress 1 (1947), 252—264, MR 8, 482] // Kaleidoscopes: Selected Writings of H.S.M. Coxeter / edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss. — Wiley-Interscience Publication, 1995. — ISBN 978-0-471-01003-6.
- H.S.M. Coxeter. (Paper 10), Star Polytopes and the Schlafli Function f(α,β,γ) [Elemente der Mathematik 44 (2) (1989) 25-36] // Kaleidoscopes: Selected Writings of H.S.M. Coxeter / edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss. — Wiley-Interscience Publication, 1995. — ISBN 978-0-471-01003-6.
- P. Cromwell. Polyhedra. — Cabridgre University Press, Hbk., 1997.
- Field, J. V. A Lutheran astrologer: Johannes Kepler. — Archive for History of Exact Sciences. — 1984. — Vol. 31, No. 3. — P. 207—219.
- Theoni Pappas. (The Kepler-Poinsot Solids) The Joy of Mathematics. — San Carlos, CA: Wide World Publ./Tetra, 1989. — P. 113.
- Louis Poinsot. Memoire sur les polygones et polyèdres. — J. de l'École Polytechnique. — 1810. — Vol. 9. — P. 16-48.
- Lakatos, Imre. Proofs and Refutations. — Cambridge University Press, 1976.
- Schläfli, Ludwig. Theorie der vielfachen Kontinuität / editor J. H.Graf. — Republished by Cornell University Library historical math monographs 2010. — Zürich, Basel: Georg & Co., 1901. — ISBN 978-1-4297-0481-6.
- Wenninger, Magnus. Dual Models. — Cambridge University Press, 1983. — P. 39-41. — ISBN 0-521-54325-8.
Ссылки[править | править код]
- Paper models of Kepler-Poinsot polyhedra (англ.). Дата обращения: 20 ноября 2015.
- Free paper models (nets) of Kepler-Poinsot polyhedra (англ.). Дата обращения: 20 ноября 2015.
- The Uniform Polyhedra (англ.). Дата обращения: 20 ноября 2015.
- VRML models of the Kepler-Poinsot polyhedra (англ.). Дата обращения: 20 ноября 2015.
- Stellation and facetting — a brief history (англ.). Дата обращения: 20 ноября 2015.
- Stella: Polyhedron Navigator (англ.). Дата обращения: 20 ноября 2015.
Эта статья входит в число добротных статей русскоязычного раздела Википедии. |


