Пятиугольник

Пятиугольник — многоугольник с пятью углами. Также пятиугольником называют всякий предмет такой формы.

Площадь пятиугольника без самопересечений

Площадь пятиугольника без самопересечений, заданного координатами вершин, определяется по общей для многоугольников формуле.

Выпуклый пятиугольник

Выпуклым пятиугольником называется пятиугольник, такой, что все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.

Сумма внутренних углов выпуклого пятиугольника равна 540°.

$\sum {\alpha =}(n - 2) \cdot 180^\circ = 3 \cdot 180^\circ = 540^\circ$

Любые 9 точек в общем положении содержат вершины выпуклого пятиугольника и существует множество из 8 точек в общем положении, в котором нет выпуклого пятиугольника . Доказано также, что в любые 10 точек на плоскости в общем положении содержат выпуклый пустой пятиугольник. И существует множество из 9 точек в общем положении, в котором нет выпуклого пустого пятиугольника.

Правильный пятиугольник (пентагон)

Правильный пятиугольник

Пентагоном или правильным пятиугольником называется пятиугольник, у которого все стороны и углы равны. Если провести в пентагоне диагонали, то он разобьётся на:

• меньший пентагон (образуеся точками пересечения диагоналей) — в центре
• Вокруг меньшего пентагона — пять равнобедренных треугольников двух видов (с отношением бедра к основанию равным золотой пропорции):
  • 1) имеют острые углы в 36° при вершине и острые углы в 72° при основании
  • 2) имеют тупой угол в 108° при вершине и острые углы в 36° при основании

При соединении двух первых и двух вторых треугольников их основаниями, то получится два «золотых» ромба (первый имеет острый угол в 36° и тупой угол в 144°). Роджерс Пенроуз использовал «золотые» ромбы для конструирования «золотого» паркета (был назван плитками Пенроуза).

Звездчатые пятиугольники

Золотые сечения пентаграммы

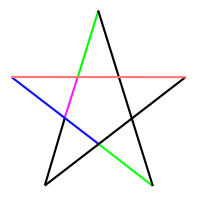
Многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника называется звёздчатым. Помимо правильного существует ещё один звёздчатый пятиугольник - пентаграмма.

Пентаграмма, как полагал Пифагор, представляет собой математическое совершенство, поскольку демонстрирует золотое сечение (φ = (1+√5)/2 = 1,618…). Если разделить длину любого цветного отрезка на длину самого длинного из оставшихся меньших отрезков, то будет получено золотое сечение φ.

$\varphi = \frac{\mathrm{\color{red}red}}{\mathrm{\color{Blue}blue}} = \frac{\mathrm{\color{Blue}blue}}{\mathrm{\color{Green}green}} = \frac{\mathrm{\color{Green}green}}{\mathrm{\color{Magenta}magenta}}$

См. также

• Правильный пятиугольник
• Пентагон
• Пентаграмма