Интервал (музыка)
Интерва́л (от лат. intervallum — промежуток, расстояние; разница, несходство) в музыке — соотношение двух музыкальных звуков по их высоте[1]. В европейской теории музыки мерой исчисления музыкальных интервалов на протяжении столетий был целый тон, по отношению к которому определялись и меньшие (например, полутон, четвертитон) и некоторые бо́льшие (например, дитон, полудитон, тритон) интервалы. Наименьшим музыкальным интервалом в европейской традиции считается полутон. Интервалы меньше полутона именуются микроинтервалами. Консонантные и диссонантные интервалы — важнейшие элементы гармонии.
Две стороны интервала[править | править код]
С одной стороны, интервал может быть представлен как математическая (акустическая) величина, выражающая отношение двух чисел — частот основных гармоник входящих в него звуков . В теоретически «правильных», то есть наиболее естественно звучащих, интервалах частоты должны соотноситься как небольшие целые числа, например 3:2 для квинты[2][3]. В равномерно темперированном строе отношения слегка отклоняются от «правильных» (скажем, 1,498307 вместо 3:2). Иногда вместо отношения используют эквивалентную величину разности логарифмов частот ( цент для 3:2). Абсолютная математическая величина интервала устанавливается путём механических (на монохорде и др.) или электронных (с помощью прикладной компьютерной программы) измерений.
С другой стороны, интервал — категория специфически музыкальной логики, что проявляет себя уже в музыкальной терминологии. Например, термин quinta предполагает понятие о пяти ступенях диатонического звукоряда (пятая ступень [quinta vox] рассчитывается от основания интервала, которое называется «примой»). Из контекста, который предоставляет музыкальная нотация (буквенная, линейная и т. д.), выводится именно музыкально-логическое значение интервала.
Интервал как математическая (акустическая) величина не может быть однозначно ассоциирован с нотированным музыкальным интервалом. Например, запись eis-a («ми диез» — «ля») в классическом учении о гармонии трактуется как хроматический интервал (уменьшённая кварта, подразумевается разрешение ми диеза в фа диез), энгармонически равный большой терции равномерно темперированного строя, в другом контексте может означать и пифагорейский дитон, и большую терцию чистого строя (например, в итальянском мадригале XVI века). Интервал, нотированный как fis-a («фа диез» — «ля»), в тональности C-dur (до мажор) может рассматриваться как малая терция равномерно темперированного строя, а в тетрахорде хроматического рода у греков — как полуторатон, или полудитон, и т. д.
Поскольку нотация фиксирует только музыкальную (а не математическую) сторону интервалов, вопрос об акустической «правильности» их звучания в каждой конкретной интерпретации нотного памятника остаётся открытым, особенно в отношении так называемой старинной музыки. Неоднозначность связи «числа» и «гармонической логики» интервала открывает простор для музыковедческих и исполнительских трактовок нотированной музыки.
Классификация интервалов[править | править код]
Универсальной и общепринятой классификации музыкальных интервалов, которые были объектом изучения на протяжении более двух тысячелетий, не существует. Нижеследующая классификация основана на сведениях из российских пособий по элементарной теории музыки (ЭТМ) 2-й половины XX и начала XXI века. Используемая в этих пособиях терминология (в том числе, интервальная) ориентирована на мажорно-минорную тональность (например, хроматика рассматривается как надстройка над диатоникой, отсюда хроматические интервалы — как производные от диатонических). Остальные исторические и локально-специфические звуковысотные системы (например, нейтральная, или зальзалева, терция, издревле присущая арабской музыкальной традиции) в ЭТМ рассматриваются по минимуму или не рассматриваются вовсе.
По изложению[править | править код]
В музыкальной теории и практике словом «интервал» обозначают не только расстояние между двумя звуками, но и само сочетание этих звуков, нижний из которых называется основанием интервала, а верхний — вершиной[4]. Вследствие этого возможны два способа изложения интервала: мелодический и гармонический[4]. Звуки интервала, взятые последовательно от основания к вершине образуют восходящий мелодический интервал; от вершины к основанию — нисходящий мелодический интервал. Звуки интервала, взятые одновременно, образуют гармонический интервал. Иначе мелодические интервалы называются горизонтальными, а гармонические — вертикальными (по их принадлежности к категориям музыкальной горизонтали или вертикали)[5].
По ширине[править | править код]
Интервалы различаются по ширине, определяемой количеством охватываемых ими ступеней звукоряда (количественной величиной)[6]. Те из них, которые образуются в пределах октавы, называются простыми. Некоторые авторы также выделяют категории тесных интервалов (от примы до кварты включительно) и широких (от квинты до октавы включительно)[7]. Интервалы шире октавы называются составными, так как они состоят из октавы и простого интервала[4]. Составные интервалы наследуют свойства простых (например, ноны, как и секунды, могут быть большими и малыми)[8]. Интервалы шире двойной октавы (квинтдецимы) в теории музыки по традиции не рассматриваются. Число, обозначающее количество ступеней, которые охватывает данный интервал, является его кратким обозначением.
По виду[править | править код]
Интервалы имеют различную качественную величину, то есть заключают в себе неодинаковое количество целых тонов и полутонов[6]. Вследствие этого однородные интервалы (интервалы идентичной ширины) могут быть не тождественны друг другу[6]. Измерение интервалов по количеству полутонов определяет различные виды интервалов одного названия[4]. Так, выделяют интервалы чистые (сокращённо — ч.), малые (м.), большие (б.), увеличенные (ув.), уменьшённые (ум.), дважды увеличенные (дв. ув.) и дважды уменьшённые (дв. ум.).
- Термины «большой» и «малый» относят к интервалам, имеющим по два основных вида[7]: это секунды, терции, сексты и септимы.
- Термин «чистый» относят к интервалам, имеющим один основной вид[7]: это примы, кварты, квинты и октавы. Такое название связано с тем, что в существовавших в разные времена строях указанные интервалы акустически точно соответствовали унисону, кварте, квинте и октаве натурального звукоряда[9]. В настоящее время, в связи с изменением строя (см. Равномерно-темперированный строй) термин сохранил своё первоначальное значение лишь в отношении октавы и примы[9].
- Термин «увеличенный» обозначает интервалы, которые на хроматический полутон (в случае дв. ув. — тон) шире своего чистого или большого вида[7][9].
- Термин «уменьшённый» обозначает интервалы, которые на хроматический полутон (в случае дв. ум. — тон) у́же своего чистого или малого вида[7][9].
Теоретически всякий интервал может быть увеличенным или уменьшенным на полутонов, однако в музыкальной практике уже трижды увеличенные или трижды уменьшённые интервалы не встречаются[7]. Кроме того, не существует интервала, который уступал бы своей тоновой величиной чистой приме (поэтому сама прима не бывает уменьшённой, а секунда — дважды уменьшённой).
Примеры:
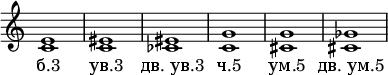
В музыке, где мажорно-минорной тональности нет (например, в додекафонии композиторов Новой венской школы), термины «уменьшённый» и «увеличенный» теряют смысл, а термин «чистый» используется только в смысле акустической чистоты (см. Чистый строй).
По впечатлению на слух[править | править код]
Начиная с античности и до эпохи мажорно-минорной тональности интервалы также распределялись по тому, насколько слитно они воспринимаются слухом (подробнее см. в статье Консонанс и диссонанс). В разных исторических классификациях теоретики выделяли (по порядку от самых благозвучных к наиболее неблагозвучным) «совершенные консонансы», «несовершенные консонансы», «несовершенные диссонансы», «совершенные диссонансы» и другие оценочные термины.
По принадлежности к диатонике и хроматике[править | править код]
Интервалы, которые образуются между основными ступенями звукоряда, называются диатоническими. Интервалы, вершина и/или основание которых содержит хроматическую ступень (то есть ступень, производную от диатонической), называются хроматическими. Все увеличенные и уменьшённые интервалы, кроме тритонов, являются хроматическими.
Список музыкальных интервалов[править | править код]
Нижеследующие таблицы иллюстрируют виды интервалов, как они стандартно описываются в пособиях по элементарной теории музыки[7][9].
| Количество ступеней |
Название | Виды | Количество тонов |
Обозначение |
|---|---|---|---|---|
| Простые интервалы | ||||
Примеры простых гармонических интервалов: | ||||
| 1 | Прима | чистая | 0 (унисон) | ч.1 |
| 2 | Секунда | малая большая |
0,5 (полутон) 1 (целый тон) |
м.2 б.2 |
| 3 | Терция | малая большая |
1,5 (полудитон) 2 (дитон) |
м.3 б.3 |
| 4 | Кварта | чистая увеличенная |
2,5 3 (тритон) |
ч.4 ув.4 |
| 5 | Квинта | уменьшенная чистая |
3 (тритон) 3,5 |
ум.5 ч.5 |
| 6 | Секста | малая большая |
4 4,5 |
м.6 б.6 |
| 7 | Септима | малая большая |
5 5,5 |
м.7 б.7 |
| 8 | Октава | чистая | 6 (октава) | ч.8 |
| Составные интервалы | ||||
Примеры составных гармонических интервалов: | ||||
| 9 | Нона (секунда + ч.8) | малая большая |
6,5 7 |
м.9 б.9 |
| 10 | Децима (терция + ч.8) | малая большая |
7,5 8 |
м.10 б.10 |
| 11 | Ундецима (кварта + ч.8) | чистая увеличенная |
8,5 9 |
ч.11 ув.11 |
| 12 | Дуодецима (квинта + ч.8) | уменьшенная чистая |
9 9,5 |
ум.12 ч.12 |
| 13 | Терцдецима (секста + ч.8) | малая большая |
10 10,5 |
м.13 б.13 |
| 14 | Квартдецима (септима + ч.8) | малая большая |
11 11,5 |
м.14 б.14 |
| 15 | Квинтдецима (октава + ч.8) | чистая | 12 | ч.15 |
| Количество ступеней | Название | Качество | Количество тонов | Обозначение | Квинтовых шагов |
| 1 | Прима | чистая | 0 | ч.1 | 0 |
| увеличенная | 0,5 | ув.1 | 7 | ||
| 2 | Секунда | малая | 0,5 | м.2 | 5 |
| большая | 1 | б.2 | 2 | ||
| увеличенная | 1,5 | ув.2 | 9 | ||
| уменьшенная | 0 | ум.2 | 12 | ||
| 3 | Терция | малая | 1,5 | м.3 | 3 |
| большая | 2 | б.3 | 4 | ||
| уменьшенная | 1 | ум.3 | 10 | ||
| увеличенная | 2,5 | ув.3 | 11 | ||
| 4 | Кварта | чистая | 2,5 | ч.4 | 1 |
| увеличенная | 3 | ув.4 | 6 | ||
| уменьшенная | 2 | ум.4 | 8 | ||
| 5 | Квинта | чистая | 3,5 | ч.5 | 1 |
| уменьшенная | 3 | ум.5 | 6 | ||
| увеличенная | 4 | ув.5 | 8 | ||
| 6 | Секста | малая | 4 | м.6 | 4 |
| большая | 4,5 | б.6 | 3 | ||
| уменьшенная | 3,5 | ум.6 | 11 | ||
| увеличенная | 5 | ув.6 | 10 | ||
| 7 | Септима | малая | 5 | м.7 | 2 |
| большая | 5,5 | б.7 | 5 | ||
| увеличенная | 6 | ув.7 | 12 | ||
| уменьшенная | 4,5 | ум.7 | 9 | ||
| 8 | Октава | чистая | 6 | ч.8 | 0 |
| уменьшенная | 5,5 | ум.8 | 7 |
В двенадцатиступенном равномерно темперированном строе, ставшем основным в европейской музыке с XVIII в., соотношение частот звуков, образующих интервал, вычисляется как , где — количество тонов (см. таблицу выше).
Обращения[править | править код]
Обращением интервала называется перемещение звука, лежащего в его основании, на октаву вверх или вершины интервала — на октаву вниз. При обращении качество интервала меняется на противоположное: большой становится малым, увеличенный — уменьшённым, дважды увеличенный — дважды уменьшённым и наоборот. Чистый интервал остаётся чистым. В простых интервалах сумма цифровых обозначений основного вида интервала и его обращения всегда равна девяти.
| Основной интервал | Обращённый интервал |
|---|---|
| Прима (1) | Октава (8) |
| Секунда (2) | Септима (7) |
| Терция (3) | Секста (6) |
| Кварта (4) | Квинта (5) |
| Квинта (5) | Кварта (4) |
| Секста (6) | Терция (3) |
| Септима (7) | Секунда (2) |
| Октава (8) | Прима (1) |
Если требуется обратить составной интервал, на октаву переносятся оба его звука (верхний — вниз, нижний — вверх) либо один из них на две октавы, при этом сумма цифровых обозначений обоих интервалов всегда равна шестнадцати.
| Основной интервал | Обращённый интервал |
|---|---|
| Нона (9) | Септима (7) |
| Децима (10) | Секста (6) |
| Ундецима (11) | Квинта (5) |
| Дуодецима (12) | Кварта (4) |
| Терцдецима (13) | Терция (3) |
| Квартдецима (14) | Секунда (2) |
| Квинтдецима (15) | Прима (1) |
Увеличенная октава, также рассматривающаяся как составной интервал, даёт в обращении октаву уменьшённую.
Возможность исполнения[править | править код]
Возможность исполнения интервалов конкретными инструментами или вокально определяется, в частности:
- диапазоном инструмента/голоса (ограничение и сверху, и снизу, причём ближе к крайним доступным регистрам качество звучания становится хуже, особенно у вокалистов);
- [для гармонического изложения] технической возможностью одновременного извлечения более одного звука (например, на ксилофоне - да, а на духовых инструментах или голосом - нет):
- растяжением руки исполнителя (например, взрослый пианист обычно способен сыграть legato одной рукой интервалы до децимы, а скрипач при ведении смычка по одной струне — не шире тритона);
- удобством интонирования (скажем, очень часто сложны широкие интервалы, особенно скачки́ [так, на рояле в быстром темпе можно не попасть на нужную клавишу], а также непривычные для соответствующей культуры интервалы типа зальзалевой терции для певцов-европейцев);
- реальностью достижения слитного звучания при групповой игре (допустим, движение октавами считается рискованным, ибо ясно ощущается малейшая фальшь).
Эти и другие исполнительские ограничения по интервалам всегда учитываются композиторами при написании музыки как для инструмента/голоса соло, так и для оркестра[11].
Примечания[править | править код]
- ↑ Назайкинский Е. В. Интервал Архивная копия от 16 апреля 2018 на Wayback Machine // Большая российская энциклопедия. Том 11. — М., 2008. — С. 435.
- ↑ В отечественном музыковедении числовое отношение интервала часто неправильно называют «пропорцией». Например, Е. В. Герцман: «…звучание должно выражаться числом… можно смело представлять звуковые отношения конкретными числовыми пропорциями. Но так как неодинаковые отношения количества представляются различными типами пропорций, то и расстояния между звуками (интервалы) способны регистрироваться аналогичным образом, то есть кратными, эпиморными, эпимерными и прочими пропорциями» (Пифагорейское музыкознание. СПб., 2003, стр. 280—281.).
- ↑ Подробно об арифметических терминах «отношение» и «пропорция» можно прочитать в учебниках арифметики, например, в Шестом отделе учебника А. С. Киселева «Систематический курс арифметики» Архивная копия от 4 декабря 2016 на Wayback Machine.
- ↑ 1 2 3 4 Красинская Л. Э., Уткин В. Ф. Элементарная теория музыки: Учеб. пособие. — М.: Музыка, 2007. — С. 84, 94, 87. — 334 с. — ISBN 978-5-7140-0764-4, ББК 85.314, К 78.
- ↑ Термины «горизонтальный интервал» и «вертикальный интервал» вошли в употребление в последние десятилетия XX века, см., например: Холопов Ю. Н. Гармония. Теоретический курс. М., 1988, с.22. В популярных доныне учебниках элементарной теории музыки, написанных в 1950-е гг. — И. В. Способина (1951), В. А. Вахромеева (1956), а также в «Практическом руководстве по музыкальной грамоте» Г. А. Фридкина (1957) — использовались только термины (соответственно) «мелодический интервал» и «гармонический интервал».
- ↑ 1 2 3 В. И. Астахова. Музыкальная грамота : Популярный справочник для тех, кто учится играть на гитаре, фортепиано, баяне и других музыкальных инструментах. — Минск: Современная школа, 2011. — С. 21, 22. — 48 с. — 3050 экз. — ISBN 978-985-539-187-7.
- ↑ 1 2 3 4 5 6 7 Алексеев Б., Мясоедов А. Глава IV. ИНТЕРВАЛЫ // Элементарная теория музыки. — Москва: Издательство «Музыка», 1986. — С. 67—69. — 240 с. — 38 000 экз.
- ↑ Интервал // Казахстан. Национальная энциклопедия. — Алматы: Қазақ энциклопедиясы, 2005. — Т. II. — ISBN 9965-9746-3-2. (CC BY-SA 3.0)
- ↑ 1 2 3 4 5 Курс теории музыки / Общая редакция А. Л. Островского. — Издание 3-е. — Издательство «Музыка», Ленинградское отделение, 1988. — С. 49, 48. — 20 000 экз.
- ↑ Битюков Сергей. 13 звуков и интервалов. Их восприятие и обозначение. Лады отклонения и модуляции (рус.). Хабр (7 августа 2021). Дата обращения: 12 августа 2021. Архивировано 12 августа 2021 года.
- ↑ М. И. Чулаки Инструменты симфонического оркестра // Изд-во «Музыка», М. (1972) — см., в частн., стр. 35 и 49.
Литература[править | править код]
- Интервал // Музыкальная энциклопедия. — М.: Советская энциклопедия, 1974. — Т. 2. — С. 544—545. — 960 с.
- Соловьёв Н. Ф. Интервал // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Фридкин Г. Практическое руководство по музыкальной грамоте. — М.: Музгиз, 1962
Ссылки[править | править код]
- Интервальные таблицы Гуго Римана
- Таблица 365 интервалов (наименования интервалов и их переводы не являются нормативными)




