Правило фаз
Пра́вило фаз (или правило фаз Гиббса) — соотношение, связывающее число компонентов, фаз и термодинамических степеней свободы в равновесной термодинамической системе[1]. Роль правила[2] фаз особенно велика при рассмотрении гетерогенных равновесий в многофазных многокомпонентных системах[3].
Хотя под термином «правило» обычно подразумевают приближенную или частную закономерность, в случае правила фаз Гиббса речь идёт о строгой и общей зависимости — законе равновесия фаз[4].
Описание состояния термодинамической фазы
[править | править код]

С точки зрения терминологии о любом растворе одинаково правильно говорить как об однородной системе и как об однофазной гомогенной системе, а о кубиках льда в воде — как о неоднородной системе и как о двухфазной гетерогенной системе. Выбор наиболее подходящего термина зависит от постановки рассматриваемой задачи, поскольку различие в терминах «термодинамическая система» и «термодинамическая фаза» отражает разницу в подходах к описанию системы и фазы. Под состоянием фазы понимают набор используемых для её описания интенсивных переменных[5][6]. Такие интенсивные величины, как плотность, теплоёмкость, коэффициент термического расширения и др. характеризуют термодинамические свойства индивидуального вещества или раствора, образующего фазу. Само понятие термодинамической фазы было введено Гиббсом с целью «иметь термин, который относится только к составу и термодинамическому состоянию […] тела и для которого не имеет значения его величина или его форма»[7][K 1] в связи с выводом правила фаз, основанном на использовании уравнения Гиббса — Дюгема. Отсюда естественным образом вытекает принадлежащее А. В. Сторонкину определение фазы как индивидуального вещества или раствора, при всех возможных условиях существования допускающего описание одним уравнением, выражающим связь между переменными состояния[9] — уравнением Гиббса — Дюгема или любым из канонических уравнений состояния. Предпочтение, отдаваемое уравнению Гиббса — Дюгема, связано с тем, что все независимые переменные в этом уравнении представляют собой интенсивные величины.
Состав каждой фазы определяется долями компонентов (мольными или массовыми). Доля каждого компонента, отсутствующего в рассматриваемой фазе, считается равной нулю[10]. Использование мольных долей требует применения для всех фаз одной и той же формульной единицы при вычислении числа молей компонента[11]. Обычно при рассмотрении фазовых равновесий исходят из того, что химические превращения в гетерогенной системе уже учтены при подсчёте числа компонентов, поэтому химические реакции в системе во внимание не принимают[12].
Иногда в дефиницию термина «фаза» вводят требование идентичности не только термодинамических, но вообще всех макроскопических свойств вещества. Например, оптически активные право- и левовращающие кристаллы (кварца, бертолетовой соли и т. п.) предлагают рассматривать как две различные фазы, отличающиеся кристаллографическими параметрами. Однако по своим термодинамическим свойствам такие вещества идентичны и их традиционно считают одной фазой[1].
В рамках термодинамики Гиббса при рассмотрении гетерогенных равновесий вещества до и после фазового перехода второго рода считают одной фазой[1]. Например, одной фазой считают α-Fe (феррит) со свойствами ферромагнетика — устойчивую ниже точки Кюри (769 °C) полиморфную модификацию железа, и β-Fe — полиморфную модификацию, отличающуюся от α-Fe магнитными свойствами (парамагнетик).
Для задания термодинамического состояния системы, т. е. всей совокупности её свойств, недостаточно знания свойств фаз, образующей эту систему: в наборе независимых переменных системы должна быть представлена хотя бы одна экстенсивная величина, например объём или масса системы[8].
Термодинамические степени свободы, вариантность и полная вариантность системы
[править | править код]В термодинамике каждой независимой интенсивной переменной состояния, значение которой можно изменять произвольно при условии, что фазы, образующие систему, не исчезают, и новые фазы не образуются, соответствует одна термодинамическая степень свободы. Числом степеней свободы (вариантностью) системы называют число независимых интенсивных переменных (для открытых термодеформационных систем это давление, температура и доли компонентов в различных фазах), значения которых необходимо знать, чтобы полностью описать состояния всех фаз системы, и которые можно одновременно произвольно задать без изменения числа и природы фаз (без изменения фазового состава системы)[13][14][10]. Число степеней свободы изучаемой системы равно разности между числом интенсивных переменных, достаточных для её полного описания, и числом связей между этими переменными, т. е. равно числу независимых переменных, допускающих произвольное варьирование, не ведущее к изменению природы системы[15].
Число независимых переменных, необходимых для задания состояния системы с учётом масс всех её фаз, называют полной (общей) вариантностью системы[8][16].
Вариантность и полная вариантность могут принимать только неотрицательные целочисленные значения, а их наименьшие значения равны нулю[13].
Пример. Закрытая система из твёрдого карбоната кальция, диссоциирующего при нагревании на твёрдый оксид кальция и газообразную двуокись углерода по реакции получения негашёной извести обжигом известняка:
- .
Имеем три составляющих вещества и одну химическую реакцию, дополнительные уравнения связи отсутствуют (поскольку в каждой фазе по одному веществу), поэтому система двухкомпонентная. Система закрытая, т. е. произвольное изменение долей компонентов невозможно; система термодеформационная, то есть воздействовать на систему можно изменением температуры и давления. Опыт показывает, что для описания состояния рассматриваемой системы достаточно одной величины. Если в качестве такой переменной выбрать температуру системы, то равновесное давление углекислого газа в замкнутой системе будет однозначно определяться заданной температурой и его нельзя произвольно менять, не теряя одну из фаз[17].
Допущения, используемые при выводе правила фаз
[править | править код]Практическое применение правила фаз в конкретной задаче предполагает предварительную проверку соблюдения допущений, обычно используемых при выводе данного правила[18]:
- в системе имеет место равновесие фаз;
- рассматривают только объёмные (трёхмерные) фазы, двумерные (поверхностные) фазы исключены из рассмотрения;
- границы между фазами плоские, не препятствуют выравниванию давления и температуры в системе и переносу вещества между фазами;
- влияние силовых полей (гравитационного, магнитного и т. п.) не учитывают, а из всех обобщённых термодинамических координат принимают во внимание только объём и массы компонентов, то есть рассматривают лишь термодеформационные системы — открытые и закрытые.
Правило фаз применимо только для систем, которые находятся в состоянии термодинамического равновесия. В природе такое равновесие обычно отсутствует. Например, весной лёд тает и исчезает, в холодное время года вода замерзает, а совместное присутствие льда и воды — явление временное. Если в рассматриваемой системе не все возможные равновесия реализуются по кинетическим причинам (слишком малы скорости процессов, ведущих к равновесию), то сделанные с помощью правила фаз выводы могут не соответствовать реальным наблюдениям.
Требование соблюдения равновесия фаз не допускает исключений (к метастабильному равновесию правило фаз неприменимо[19]), тогда как отказ от любого другого из перечисленных допущений ведёт к модификации формул правила фаз[18].
Формулировки правила фаз для различных условий изоляции системы
[править | править код]Математическая формулировка правила фаз зависит от наложенных на систему условий изоляции[20][21]. Материальная изоляция не влияет на число фаз в гетерогенной системе, но разрывает связь между числом фаз и вариантностью системы в случае, когда число фаз меньше или равно числу компонентов[22]. Если кроме соотношений, выражающих условия материальной изоляции, существуют другие уравнения связи между интенсивными переменными фаз, то вариантность и полная вариантность системы будут меньше на число этих уравнений.
Открытая система
[править | править код]Число степеней свободы (число интенсивных переменных, которым можно одновременно задать произвольные значения) открытой многокомпонентной гетерогенной системы в состоянии равновесия находят посредством соотношения, которое представляет собой математическую формулировку правила фаз Гиббса[3]:
| (Правило фаз для открытых систем) |
где — число степеней свободы, соответствующих давлению и температуре; — число компонентов системы; — число фаз в системе.
Данному правилу подчиняются все открытые равновесные системы, состоящие из любого числа фаз и любого числа компонентов (присутствие каждого компонента в любой из фаз не предполагается[23][24]). Если один из параметров — давление либо температура — фиксирован, то говорят об условном числе степеней свободы (условной вариантности)[4][25][26], вычисляемой по формуле
| (Условная вариантность открытой системы) |
Непосредственно из правила фаз следует ограничение на число сосуществующих в системе фаз:
| (Ограничение на число сосуществующих в системе фаз) |
Максимально возможное число фаз в гетерогенной системе , соответствующее нулевой вариантности, равно
| (Максимальное число фаз в гетерогенной системе) |
При использовании уравнения для систем, у которых какое-то количество параметров зафиксировано, число степеней свободы уменьшается на число фиксированных параметров[13]. Так, для конденсированных систем (например, сплавов металлов), когда давление либо постоянно, либо его влиянием на состояние равновесия можно пренебречь, вариантность системы на единицу меньше даваемого уравнением Гиббса для вариантности открытых систем[3].
Для однокомпонентной системы
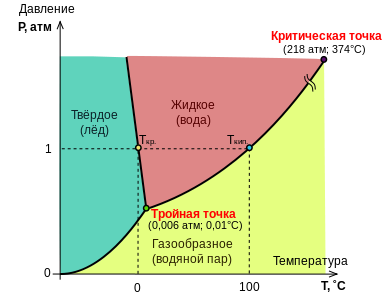
Отсюда следует, что максимальное число фаз в однокомпонентной системе, достигаемое при минимальной (нулевой) её вариантности, равно трём; ни давление, ни температуру для трёхфазной однокомпонентной системы задать произвольно нельзя. На фазовой диаграмме сосуществованию трёх фаз соответствует тройная точка с фиксированными значениями давления и температуры. При всякой другой температуре или другом давлении равновесие трёх фаз невозможно: в системе будут происходить изменения, в результате которых одна или две фазы исчезнут.
В случае энантиотропии и превращения одной полиморфной фазы в другую условие постоянства давления уменьшает вариантность системы на 1, так что переход возможен только при одной строго определённой температуре ()[27]. Например, для железа при 1394 °C имеет место обратимый переход между γ-Fe (аустенитом) с гранецентрированной кубической решёткой и δ-Fe с объёмноцентрированной кубической решёткой.
Двухфазному равновесию в однокомпонентной системе () на фазовой диаграмме соответствует линия. Температуре системы можно придать произвольное значение, но равновесное давление в обеих фазах окажется при этом заданным однозначно.
Если фаза одна (), то число степеней свободы системы равно двум, т. е. температуре и давлению можно придавать произвольные значения в пределах некоторой области на фазовой диаграмме — пока система не окажется на одной из линий двухфазного равновесия. Простейшим примером однокомпонентной однофазной системы служит жидкость, давление на которую выше, чем давление её насыщенного пара при рассматриваемой температуре; в этом случае пара над жидкостью не будет, т. е. система будет однофазной[28].
Полная вариантность открытой системы (число независимых переменных в любом из канонических уравнений состояния) равна[29][30][31]
| (Полная вариантность открытой системы) |
и не зависит от числа фаз в системе.
Закрытая система
[править | править код]| (Правило фаз для закрытых систем с числом компонентов, не превышающим числа фаз) |
т. е. вычисляется так же, как для открытой системы. Правило фаз в его традиционной форме продолжает действовать в закрытой системе до тех пор, пока число компонентов не превысит число фаз.
- Для закрытой системы, в которой число компонентов не меньше числа фаз, вариантность равна двум
| (Правило фаз для закрытых систем с числом фаз, не превышающим числа компонентов) |
- Полная вариантность любой закрытой системы при отсутствии внешних полей и поверхностных эффектов равна двум вне зависимости от числа фаз, числа компонентов и их распределения внутри системы (правило Дюгема, 1899)[34][35][36]
| (Правило Дюгема для полной вариантности закрытой системы) |
Закрытая система в жёсткой оболочке
[править | править код]Система, заключённая в жёсткую оболочку, имеет постоянный объём. Вариантность и полная вариантность такой системы равны[33]
Правило фаз в его традиционной форме применимо к рассматриваемой системе до тех пор, пока число компонентов не превысит число фаз, уменьшенное на единицу.
Закрытая система в жёсткой адиабатной оболочке (изолированная система)
[править | править код]Закрытая система, помещённая в жёсткую адиабатную оболочку, не способна к каким-либо изменениям; вариантность и полная вариантность системы равны нулю. По этой причине при рассмотрении гетерогенных равновесий свойства изолированных систем не обсуждают[37]. А. И. Русанов считает, однако, что учёт поверхностных явлений в такой системе даёт ненулевые значения вариантности и полной вариантности. А именно, для систем с плоскими поверхностями раздела между фазами в отсутствие поверхностных фазовых процессов вариантность и полная вариантность изолированной системы равны[37]
где — число поверхностей разрыва между фазами. Вариантность и полная вариантность рассматриваемой системы обусловлены исключительно наличием поверхностей: если рассматривать равновесие без учёта поверхностных явлений (), то вариантность и полная вариантность системы равны нулю. Данный подход оставляет открытым вопрос о том, как совместить представление о вариантности системы — числе допускающих изменение параметров — с требованиями выполнения условия равновесности, запрещающего внутренние процессы в системе, и условия изолированности, накладывающего запрет на любые внешние воздействия на систему.
Частично открытая система
[править | править код]Под частично открытыми понимают системы, у которых не все компоненты принимают участие в материальном обмене с окружающей средой[36]. Для таких систем проводят различие между неподвижными (инертными) компонентами, не принимающими участия в материальном обмене (масса неподвижного компонента в системе постоянна), и подвижными компонентами, массы которых непостоянны из-за участия этих компонентов в материальном обмене с окружающей средой.
Для частично открытой системы условия постоянства масс неподвижных компонентов рассматривают как уравнения связи, налагаемые на переменные системы и влияющие на её вариантность и полную вариантность, но не сказывающиеся на максимально возможном числе фаз, которое в частично открытых системах не зависит от степени материальной изоляции системы (т. е. от числа неподвижных компонентов), и которое вычисляют по приведённой выше формуле[38].
Условия постоянства объёма и/или энтропии гетерогенной системы учитывают в точности так же, как и условия материальной изоляции (в приводимые ниже выражения для вычисления вариантности и полной вариантности вместо числа неподвижных компонентов подставляют значение — при постоянстве объёма и энтропии, или — при постоянстве одной экстенсивной переменной[39]).
- Для системы, в которой число неподвижных компонентов больше числа фаз , вариантность и полная вариантность равны[40]
где — число компонентов системы, — число подвижных компонентов (). Таким образом, для рассматриваемой системы условия материальной изоляции обусловливают уменьшение числа степеней свободы, которое не зависит от числа фаз (образование новой фазы не влияет на вариантность), а равенство вариантности и полной вариантности означает невозможность фазовых процессов, не изменяющих составы фаз[41].
- Для системы, в которой число неподвижных компонентов меньше числа фаз, вариантность равна[40]
т. е. в данном случае условия материальной изоляции не накладывают ограничений на состав фаз и не сокращают число степеней свободы по сравнению с открытой системой[42].
Полная вариантность рассматриваемой системы равна[43][43][44]
Вариантность системы меньше её полной вариантности, поэтому в системе возможны фазовые процессы, не изменяющие состав фаз[42].
- Для системы, в которой число неподвижных компонентов равно числу фаз, вариантность и полная вариантность равны[43]
Таким образом, для рассматриваемой системы условия материальной изоляции не сказываются на вариантности системы, а равенство вариантности и полной вариантности означает невозможность фазовых процессов, не изменяющих составы фаз[42].
Сложная система
[править | править код]К сложным системам обычно относят диэлектрики, магнетики, сверхпроводники, поверхности раздела фаз, системы в поле тяготения и в состоянии невесомости, электрохимические системы. Для таких систем вариантность и полную вариантность гетерогенной системы находят по уравнению Гиббса для вариантности и уравнению Гиббса для полной вариантности, заменяя в них — число степеней свободы, соответствующих давлению и температуре, — на значение, учитывающее природу природу рассматриваемой системы: — для фотонного газа[45]; — для гетерогенной системы в силовом поле (электрическом, магнитном, гравитационном или центробежном)[46]. Максимально возможное число фаз в силовом поле должно превышать значение, даваемое уравнением Гиббса для вариантности в отсутствие поля, но экспериментального подтверждения этому выводу пока нет[47].
Правило фаз для поверхностных слоёв между сосуществующими фазами учитывает разницу между плоскими и искривлёнными поверхностями раздела[48][49].
Пример сложной системы — двухкомпонентные смеси
[править | править код]
В смесях двух химически невзаимодействующих компонентов так что В дополнение к температуре и давлению другой степенью свободы является химический состав каждой фазы, обычно выражаемый в виде мольной доли или массовой доли одного из компонентов.
Например, система двух жидкостей, смешивающихся в произвольном соотношении, таких как толуол и бензол, не образующих азеотропную смесь, и находящихся в равновесии с её паром, может быть описана диаграммой температуры кипения, показывающую состав двух равновесных фаз в зависимости от температуры при фиксированном давлении.
Четыре термодинамические переменные, которые могут описывать систему, включают температуру, давление, мольную долю компонента 1, например, толуола в жидкой фазе и мольную долю его же в паровой фазе. Но так как в равновесии участвуют две фазы только две из этих переменных могут быть независимыми Это обусловлено тем, что четыре переменные связаны двумя соотношениями: равенством химических потенциалов жидкого толуола и паров толуола и аналогичным равенством для бензола.
Для заданных температуре и давлении две фазы находятся в равновесии, при этом состав фазы (точка системы) находится между двумя кривыми (см. рисунок). Горизонтальная линия (изотерма или связующая линия) может быть проведена через любую такую точку системы и пересекает кривую для каждой фазы при ее равновесном составе.
Математическая интерпретация правила фаз
[править | править код]Математика позволяет описать явления природы на символическом языке различными способами. Удачная интерпретация правила фаз возможна с помощью теории графов. Уравнение Гиббса для вариантности может быть наглядно интерпретировано как соотношение между вершинами, рёбрами, гранями и объёмами некоего графа.
Классификация термодинамических систем по вариантности
[править | править код]В зависимости от числа степеней свободы (вариантности) различают системы нонвариантные (безвариантные, ), моновариантные (), бивариантные (дивариантные, ), … и поливариантные[3][50].
В нонвариантных системах с нулевой полной вариантностью фазовые реакции (переходы компонентов между фазами) невозможны. Число фаз такой системе максимально[22]. В нонвариантных системах с отличной от нуля полной вариантностью возможно протекание фазовых реакций без нарушения равновесия системы[51][32].
Использование правила фаз
[править | править код]Применение правила фаз не требует конкретизации перечня компонентов системы — достаточно знать их общее число.
Правило фаз особенно полезно при исследовании гетерогенных систем, в частности в металловедении, металлургии, петрографии, химической технологии, поскольку является теоретической основой для анализа диаграмм состояния любой степени сложности[52]. Правило фаз позволяет сразу же определить метрику такой диаграммы, поскольку минимально возможная вариантность системы равна нулю, а минимальное число фаз — одна. Так, для характеристики состояния однокомпонентной системы (две степени свободы) необходимы две переменные ( и ), т. е. диаграмма состояния однокомпонентной системы плоская. Диаграмма состояния двухкомпонентной системы характеризуется тремя параметрами (, и одна из концентраций). Такая диаграмма — объёмная, для построения её проекции на плоскости необходимо зафиксировать одну из переменных. Соответственно получаем три типа диаграмм двухкомпонентных систем на плоскости: изотерму, изобару и изопикну (изодолю)[53]. Полная диаграмма состояния трёхкомпонентной системы требует для своего описания уже четырёхмерного пространства. Объёмную диаграмму, в основании которой обычно лежит треугольник Гиббса — Розебома, строят чаще всего при или
Минералогическое правило фаз
[править | править код]В. Гольдшмидт, изучая скарны Южной Норвегии, обратил внимание на то, что наблюдаемые им парагенезисы минералов были тем пестрее, чем больше они содержали компонентов. Это послужило ему основанием применить правило фаз Гиббса и сформулировать минералогическое правило фаз (1911): «Максимальное число твёрдых минералов, которые одновременно совместно устойчиво существуют, равно числу компонентов, составляющих эти минералы»[54].
Горные породы образуются при произвольных значениях температуры и давления, так что число степеней свободы в уравнении Гиббса для вариантности не может быть меньше двух. Поэтому в условиях термодинамического равновесия число минералов (фаз), слагающих горную породу, не может превышать числа её компонентов (обычно простых веществ или окислов)[55]:
| (Минералогическое правило фаз Гольдшмидта) |
Д. С. Коржинский ввёл представление о неподвижных (инертных) и подвижных компонентах и дал новую формулировку минералогическому правилу фаз, согласно которой подвижные компоненты на число фаз не влияют[56], а число минералов (фаз), слагающих горную породу, не может превышать числа её неподвижных (инертных) компонентов[55]:
| (Минералогическое правило фаз Коржинского) |
Историческая справка
[править | править код]Правило фаз вывел Дж. Гиббс (опубликовано в 1876 году); название «правило фаз» предложено У. Банкрофтом[57]. Правило фаз широко использовали в конце XIX — начале XX века Я. Вант-Гофф, Х. Розебом и их ученики, Н. С. Курнаков и его школа. В. Гольдшмидт сформулировал минералогическое правило фаз (1911), а Д. С. Коржинский дал ему новую формулировку, разделив компоненты геологических систем на инертные (в смысле транспортных свойств) и вполне подвижные (т. е. способные свободно перемещаться через границы системы). А. В. Сторонкин получил строгие формулировки правила фаз для частично открытых систем.
См. также
[править | править код]- Равновесие фаз
- Критическая точка (термодинамика)
- Правила Коновалова
- Правило Розебома
- Правило Оствальда
- Тройная точка
- Фазовая диаграмма
Комментарии
[править | править код]- ↑ Если для задания термодинамического состояния фазы достаточно интенсивных переменных, а знание экстенсивных величин (массы фазы или её объёма) не требуется, то для задания термодинамического состояния системы, то есть всей совокупности свойств системы, недостаточно знания свойств образующих эту систему фаз: в наборе независимых переменных для системы должна быть представлена хотя бы одна экстенсивная величина, например объём или масса системы[8].
Примечания
[править | править код]- ↑ 1 2 3 Химическая энциклопедия, т. 5, 1998, с. 53.
- ↑ «Правило» — традиционно используемый термин для совершенно строгой (в рамках сделанных при выводе допущений) теоремы термодинамики.
- ↑ 1 2 3 4 БСЭ, 3-е изд., т. 27, 1977, с. 181.
- ↑ 1 2 Карапетьянц М. Х., Химическая термодинамика, 2013, с. 122.
- ↑ Воронин Г. Ф., Основы термодинамики, 1987, с. 13.
- ↑ Залевски К., Феноменологическая и статистическая термодинамика, 1973, с. 9.
- ↑ Гиббс Дж. В., Термодинамические работы, 1950, с. 143.
- ↑ 1 2 3 Воронин Г. Ф., Основы термодинамики, 1987, с. 15.
- ↑ Сторонкин А. В., Термодинамика гетерогенных систем, ч. 1—2, 1967, с. 109.
- ↑ 1 2 Акопян А. А., Химическая термодинамика, 1963, с. 334.
- ↑ Сторонкин А. В., Термодинамика гетерогенных систем, ч. 1—2, 1967, с. 28.
- ↑ Поляченок О. Г., Поляченок Л. Д., Физическая и коллоидная химия, 2008, с. 62—63.
- ↑ 1 2 3 Поляченок О. Г., Поляченок Л. Д., Физическая и коллоидная химия, 2008, с. 63.
- ↑ Пригожин И., Дефэй Р., Химическая термодинамика, 1966, с. 179.
- ↑ Серафимов Л. А. и др. Правило фаз, 2008, с. 6—7.
- ↑ Русанов А. И., Фазовые равновесия и поверхностные явления, 1967, с. 38.
- ↑ Холохонова Л. И., Молдагулова Н. Е., Учение о фазовых равновесиях, 2009, с. 11—12.
- ↑ 1 2 Серафимов Л. А. и др. Правило фаз, 2008, с. 18—19.
- ↑ Булидорова Г. В. и др., Физическая химия, 2012, с. 222.
- ↑ Сторонкин А. В., Термодинамика гетерогенных систем, ч. 1—2, 1967, с. 118—119, 125.
- ↑ Русанов А. И., Фазовые равновесия и поверхностные явления, 1967, с. 38—43.
- ↑ 1 2 Серафимов Л. А. и др. Правило фаз, 2008, с. 28.
- ↑ Серафимов Л. А. и др. Правило фаз, 2008, с. 20.
- ↑ Пригожин И., Дефэй Р., Химическая термодинамика, 1966, с. 180.
- ↑ Евстратова К. И. и др., Физическая и коллоидная химия, 1990, с. 120.
- ↑ Аносов В. Я., Погодин С. А., Основные начала физико-химического анализа, 1947, с. 547.
- ↑ Жуховицкий А. А., Шварцман Л. А., Физическая химия, 1987, с. 164.
- ↑ Акопян А. А., Химическая термодинамика, 1963, с. 338.
- ↑ Жариков В. А., Основы физической геохимии, 2005, с. 53..
- ↑ Воронин Г. Ф., Основы термодинамики, 1987, с. 23.
- ↑ Сторонкин А. В., Термодинамика гетерогенных систем, ч. 1—2, 1967, с. 121.
- ↑ 1 2 Сторонкин А. В., Термодинамика гетерогенных систем, ч. 1—2, 1967, с. 126.
- ↑ 1 2 Русанов А. И., Фазовые равновесия и поверхностные явления, 1967, с. 39.
- ↑ Серафимов Л. А. и др. Правило фаз, 2008, с. 24.
- ↑ Химическая энциклопедия, т. 2, 1990, с. 160.
- ↑ 1 2 Сторонкин А. В., Термодинамика гетерогенных систем, ч. 1—2, 1967, с. 122.
- ↑ 1 2 Русанов А. И., Фазовые равновесия и поверхностные явления, 1967, с. 43.
- ↑ Сторонкин А. В., Термодинамика гетерогенных систем, ч. 1—2, 1967, с. 128.
- ↑ Сторонкин А. В., Термодинамика гетерогенных систем, ч. 1—2, 1967, с. 128—129.
- ↑ 1 2 Сторонкин А. В., Термодинамика гетерогенных систем, ч. 1—2, 1967, с. 122—123.
- ↑ Сторонкин А. В., Термодинамика гетерогенных систем, ч. 1—2, 1967, с. 125, 127.
- ↑ 1 2 3 Сторонкин А. В., Термодинамика гетерогенных систем, ч. 1—2, 1967, с. 125.
- ↑ 1 2 3 Сторонкин А. В., Термодинамика гетерогенных систем, ч. 1—2, 1967, с. 124.
- ↑ Русанов А. И., Фазовые равновесия и поверхностные явления, 1967, с. 439.
- ↑ Алмалиев А. Н. и др., Термодинамика и статистическая физика, 2004, с. 59.
- ↑ Сторонкин А. В., Термодинамика гетерогенных систем, ч. 1—2, 1967, с. 129.
- ↑ Серафимов Л. А. и др. Правило фаз, 2008, с. 33.
- ↑ Сторонкин А. В., Термодинамика гетерогенных систем, ч. 1—2, 1967, с. 129—131.
- ↑ Русанов А. И., Фазовые равновесия и поверхностные явления, 1967, с. 34—43.
- ↑ Сторонкин А. В., Термодинамика гетерогенных систем, ч. 1—2, 1967, с. 98.
- ↑ Серафимов Л. А. и др. Правило фаз, 2008, с. 11.
- ↑ Поляченок О. Г., Поляченок Л. Д., Физическая и коллоидная химия, 2008, с. 61.
- ↑ Поляченок О. Г., Поляченок Л. Д., Физическая и коллоидная химия, 2008, с. 64.
- ↑ Минералогическое правило фаз // Геологический словарь, [[Всероссийский научно-исследовательский геологический институт имени А. П. Карпинского|ВСЕГЕИ]]. Дата обращения: 31 мая 2015. Архивировано 27 сентября 2020 года.
- ↑ 1 2 Жариков В. А., МаракушевА. А. Минералогическое правило фаз // БСЭ (3-е изд.). Дата обращения: 10 июня 2017. Архивировано из оригинала 9 сентября 2017 года.
- ↑ Жариков В. А., Основы физической геохимии, 2005, с. 62—63.
- ↑ Kipnis A. Ya., J. W. Gibbs and chemical thermodynamics, 1991, p. 499.
Литература
[править | править код]- Акопян А. А. Химическая термодинамика. — М.: Высшая школа, 1963. — 527 с.
- Алмалиев А. Н., Копытин И. В., Корнев А. С., Чуракова Т. А. Термодинамика и статистическая физика: Статистика идеального газа. — Воронеж: Ворон. гос. ун-т, 2004. — 79 с.
- Аносов В. Я., Погодин С. А. Основные начала физико-химического анализа. — М.: Изд-во АН СССР, 1947. — 876 с.
- Большая Советская Энциклопедия / Гл. ред. А. М. Прохоров. — 3-е изд. — М.: Советская Энциклопедия, 1977. — Т. 27: Ульяновск — Франкфорт. — 622 с.
- Булидорова Г. В., Галяметдинов Ю. Г., Ярошевская Х. М., Барабанов В. П. Физическая химия. — Казань: Изд-во Казан. нац. исслед. технол. ун-та, 2012. — 396 с. — ISBN 978-5-7882-1367-5.
- Воронин Г. Ф. Основы термодинамики. — М.: Изд-во Моск. ун-та, 1987. — 192 с.
- Гиббс Дж. В. Термодинамические работы / Пер. с англ. под ред. проф. В. К. Семенченко. — М. — Л.: Гостехтеориздат, 1950. — 492 с. — (Классики естествознания).
- Гиббс Дж. В. Термодинамика. Статистическая механика / Отв. ред. Д. Н. Зубарев. — М.: Наука, 1982. — 584 с. — (Классики науки).
- Древинг В. П., Калашников Я. А. Правило фаз с изложением основ термодинамики. — 2-е изд. перераб. и доп. — М.: Изд-во Московского ун-та, 1964. — 456 с.
- Евстратова К. И., Купина Н. А., Малахова Е. Е. Физическая и коллоидная химия. — М.: Высшая школа, 1990. — 488 с. — ISBN 5-06-001018-X.
- Жариков В. А. Основы физической геохимии. — М.: Наука; Изд-во МГУ, 2005. — 656 с. — (Классический университетский учебник). — ISBN 5-211-04849-0, 5-02-035302-7.
- Жуховицкий А. А., Шварцман Л. А. Физическая химия. — 4-е изд., перераб. и доп. — М.: Металлургия, 1987. — 688 с.
- Залевски К. Феноменологическая и статистическая термодинамика: Краткий курс лекций / Пер. с польск. под. ред. Л. А. Серафимова. — М.: Мир, 1973. — 168 с.
- Карапетьянц М. Х. Химическая термодинамика. — М.: Либроком, 2013. — 584 с. — ISBN 978-5-397-03700-6.
- Поляченок О. Г., Поляченок Л. Д. Физическая и коллоидная химия. — Могилев: Могилев. гос. ун-т продовольствия, 2008. — 196 с.
- Пригожин И., Дефэй Р. Химическая термодинамика / Пер. с англ. — Новосибирск: Наука, 1966. — 506 с.
- Русанов А. И. Фазовые равновесия и поверхностные явления. — Л.: Химия, 1967. — 388 с.
- Серафимов Л. А., Фролкова А. К., Хахин Л. А. Правило фаз. — М.: МИТХТ, 2008. — 48 с.
- Сторонкин А. В. Термодинамика гетерогенных систем. Части 1 и 2. — М.: Изд-во Ленингр. ун-та, 1967. — 448 с.
- Химическая энциклопедия / Гл. ред. И. Л. Кнунянц. — М.: Советская энциклопедия, 1990. — Т. 2: Даффа реакция — Меди сульфат. — 672 с. — ISBN 5-85270-035-5.
- Химическая энциклопедия / Гл. ред. И. Л. Кнунянц. — М.: Большая Российская энциклопедия, 1992. — Т. 3: Меди сульфиды — Полимерные красители. — 640 с. — ISBN 5-85270-039-8.
- Химическая энциклопедия / Гл. ред. Н. С. Зефиров. — М.: Большая Российская энциклопедия, 1998. — Т. 5: Триптофан — Ятрохимия. — 783 с. — ISBN 5-85270-310-9.
- Холохонова Л. И., Молдагулова Н. Е. Учение о фазовых равновесиях. — Кемерово: Кемер. технол. ин-т пищ. пром-ти, 2009. — 128 с.
- Kipnis A. Ya. J. W. Gibbs and chemical thermodynamics (англ.) // Thermodynamics: History and Philosophy. Facts, Trends, Debates. — Editors K. Martinás, L. Ropolyi & P. Szegedi. — World Scientific Publishing, 1991. — P. 492—507.
Ссылки
[править | править код]- Путляев В. И., Еремина Е. А.Правило фаз (однокомпонентные системы) Архивная копия от 24 мая 2006 на Wayback Machine




















































