Квантовая химия
Ква́нтовая хи́мия — направление теоретической химии, рассматривающее строение и свойства химических соединений, реакционную способность, кинетику и механизм химических реакций на основе квантовой механики[1]. Разделами квантовой химии являются: квантовая теория строения молекул, квантовая теория химических связей и межмолекулярных взаимодействий, квантовая теория химических реакций и реакционной способности и др.[2] Она занимается рассмотрением химических и физических свойств веществ на атомарном уровне (моделях электронно-ядерного строения и взаимодействий, представленных с точки зрения квантовой механики). Вследствие того, что сложность изучаемых объектов во многих случаях не позволяет находить явные решения уравнений, описывающих процессы в химических системах, применяют приближенные методы расчета. С квантовой химией неразрывно связана вычислительная химия — дисциплина, использующая математические методы квантовой химии, адаптированные для создания специальных компьютерных программ, используемых для расчета молекулярных свойств, амплитуды вероятности нахождения электронов в атомах, симуляции взаимодействия молекул.
Общие сведения[править | править код]
Основной задачей квантовой химии является решение уравнения Шрёдингера и его релятивистского варианта (уравнение Дирака) для атомов и молекул. Уравнение Шрёдингера решается аналитически лишь для немногих систем (например, для моделей типа жёсткий ротатор (модель, описывающая линейные молекулы с постоянным межъядерным расстоянием, в такой модели уровни энергии зависят только от вращательного квантового числа), гармонический осциллятор, одноэлектронная система). Реальные многоатомные системы содержат большое количество взаимодействующих электронов, а для таких систем не существует аналитического решения этих уравнений, и, по всей видимости, оно не будет найдено и в дальнейшем. По этой причине в квантовой химии приходится строить различные приближённые решения. Из-за быстрого роста сложности поиска решений с ростом сложности системы и требований к точности расчёта, возможности квантовохимических расчётов сильно ограничиваются текущим развитием вычислительной техники, хотя, наблюдаемые в последние два десятилетия революционные сдвиги в развитии компьютерной техники, приведшие к её заметному удешевлению, заметно стимулируют развитие прикладной квантовой химии. Решение уравнения Шрёдингера часто строится на уравнении Хартри — Фока — Рутана итерационным методом (SCF-self consistent field — самосогласованное поле) и состоит в нахождении вида волновой функции.
Приближения, используемые в квантовой химии:
- Приближение Борна — Оппенгеймера (адиабатическое): движение электронов и движение ядер разделено (ядра движутся настолько медленно, что при расчёте движения электронов ядра можно принять за неподвижные объекты). В связи с этим приближением существует так называемый эффект Яна — Теллера. Данное приближение позволяет представить волновую функцию системы как произведение волновой функции ядер и волновой функции электронов.
- Одноэлектронное приближение (или приближение Хартри): считается, что движение электрона не зависит от движения других электронов системы. В связи с этим в уравнения, используемые в квантовой химии вносятся поправки на взаимное отталкивание электронов. Это позволяет волновую функцию электронов представить в виде линейной комбинации волновых функций отдельных электронов.
- Приближение МО ЛКАО (молекулярная орбиталь как линейная комбинация атомных орбиталей): в данном подходе одноэлектронная волновая функция молекулы представляется как сумма атомных орбиталей с коэффициентами:
- Ψ(r)=c1ψ1+ c2ψ2+…+cnψn,
где Ψ(r) — молекулярная орбиталь,
ci — коэффициент вхождения (амплитуда вероятности) i-той атомной орбитали в молекулярную орбиталь,
ψi — волновая функция i-той атомной орбитали (получается при решении уравнения Шрёдингера для водородоподобного атома — известно в точном виде).
Решение задачи состоит в нахождении коэффициентов сi. При учёте всех интегралов — так называемый метод Ab initio — количество вычислений растёт пропорционально количеству электронов в 6—8 степени, при полуэмпирических методах — в 4—5 степени.
Получаемая при решении уравнения волновая функция описывает чистое квантовое состояние системы. Квадрат модуля волновой функции характеризует плотность вероятности обнаружения системы в заданной точке конфигурационного пространства. Эту интерпретацию впервые предложил Макс Борн, которому за фундаментальные исследование в области квантовой механики, в частности за статистическую (вероятностную) интерпретацию волновой функции, в 1954 году была присуждена Нобелевская премия по физике.
Строение атома[править | править код]

А́том (от др.-греч. ἄτομος — неделимый) — наименьшая часть химического элемента, являющаяся носителем его свойств[3].
Атом состоит из атомного ядра и электронов. При этом порядковый номер элемента (Z) соответствует числу протонов (Z) в атомном ядре, определяет суммарный положительный электрический заряд (Ze) атомного ядра, несущего почти всю массу атома (более чем 99,9 %), а также число электронов (Z) в нейтральном атоме, определяющих его размер[4]. Электроны образуют электронную оболочку атома. Заполнение электронных оболочек подчиняется принципу Паули — в атоме не может быть двух электронов (принцип запрета Паули относится к фермионам, электроны таковыми и являются), имеющих одинаковый набор всех четырёх квантовых чисел. Ёмкость уровней электронных оболочек по мере удаления от ядра увеличивается и составляет 2 (n = 1), 8 (n = 2), 18 (n = 3), 32 (n = 4) и т. д. электронов. Слои электронных оболочек с главным квантовым числом {{{1}}} обозначаются соответственно прописными буквами K, L, M, N… Порядок заполнения подслоя электронных оболочек подчиняется правилу Хунда — суммарное спиновое число электронов данного подслоя должно быть максимальным. Распределение электронов в атомах называют электронной конфигурацией. Электронная конфигурация обозначается при помощи показателей степени, которые указывают число электронов на электронной оболочке 1s, 2s, 2p и т. д. Буквы s, p, d, f символизируют последовательные значения орбитального квантового числа l (l соответственно равно 0, 1, 2, 3)[5].
Согласно представлениям квантовой механики, атомы не имеют определённых границ, однако вероятность найти электрон, связанный с данным ядром, на расстоянии r от ядра быстро падает с увеличением r. Поэтому атому можно приписать некоторый размер[6].
Радиальная функция распределения вероятности нахождения электрона в атоме водорода обладает максимум при α0, как показано на рис. 1. Этот наиболее вероятный радиус для электрона совпадает с боровским радиусом. Более размытое облако плотности вероятности, полученные при квантовомеханическом рассмотрении, значительно отличается от боровской модели атома и согласуется с принципом неопределённости Гейзенберга[7].
Лучшим описанием эффективных размеров изолированного атома является теоретически рассчитанное положение его наружных электронов. Это так называемый орбитальный радиус атома. В зависимости от порядкового номера элемента (Z) проявляется чёткая периодичность в изменении значений орбитальных атомных радиусов[8]. Размер электронной оболочки атома более чем в 10 тысяч раз превышает размер его атомного ядра.
Ядро атома состоит из положительно заряженных протонов и незаряженных нейтронов. Если число протонов в ядре совпадает с числом электронов, то атом в целом оказывается электрически нейтральным. В противном случае он обладает некоторым положительным или отрицательным зарядом и называется ионом. Атомы классифицируются по количеству протонов и нейтронов в ядре: количество протонов определяет принадлежность атома некоторому химическому элементу, а сумма числа нейтронов и протонов — изотопу этого элемента.
Образование химической связи и строение молекул и твёрдых тел[править | править код]
Единственной молекулярной системой, для которой уравнение Шрёдингера может быть решено аналитически, является молекулярный ион водорода H2+, где единственный электрон движется в поле двух ядер (протонов). Длина химической связи в молекулярном ионе водорода H2+ составляет 1,06 Å. Энергия разрыва химической связи в молекулярном ионе водорода H2+ составляет 61 ккал/моль. Энергия притяжения электрона к обоим ядрам в одноэлектронной химической связи компенсирует энергию отталкивания протонов, которая на расстоянии 1,06 Å составляет 314 ккал/моль.
H + H+ → H2+ + 61 ккал/моль[9].
Поскольку точное решение уравнения Шрёдингера для атомно-молекулярных систем, содержащих более одного электрона, невозможно, возник ряд приближённых теорий химической связи.
- теория валентных связей, заложенная в 1927 году Гайтлером и Лондоном и развитая Слэтером и Полингом. Разработаны теория гибридизации атомных орбиталей, концепции сигма- и пи- связей.
- теория молекулярных орбиталей, появившаяся в конце 20-х годов в работах Ленарда-Джонса, Малликена и Хунда.
- теория кристаллического поля, заложенная в фундаментальных работах Бете в 1929 году, а затем развитая Ван Флеком. Разнообразные химические применения в виде теории поля лигандов эта теория получила уже в 50-х годах благодаря трудам Оргела, Иоргенсена и Бальхаузена.
- теория функционала плотности, основанная на классической модели Томаса — Ферми 1927 года, развитая Вальтером Коном. Теория пригодна для расчётов в физике твёрдого тела поверхностей Ферми многих металлов. Сложности возникают при расчёте дисперсионного взаимодействия нейтральных атомов и молекул и делают указанную теорию малопригодной для систем, в которых дисперсионные силы являются преобладающими, например, в органических соединениях.
В 1958 г. на симпозиуме по теоретической органической химии, посвящённой памяти А.Кекуле, Полинг представил теорию изогнутой химической связи. Двойная и тройная химическая связь рассматривалась, как комбинация двух или трёх изогнутых одинарных связей[10].
Правила равного удаления электронов друг от друга непосредственно следует из закона Кулона, согласно которому электроны стремятся находиться на максимально удалённом расстоянии друг от друга. Например, молекулы типа BeH2 имеют строго линейную конфигурацию. Атомы III группы таблицы Менделеева образуют тригональные молекулы, типа BF3. Атомы IV группы образуют тетраэдрические молекулы, типа CH4. Молекулы, образованные атомами V и VI групп, имеют геометрию тригональной бипирамиды и октаэдра, соответственно[11].
Физические, в том числе спектральные свойства атомов, молекул и твёрдых тел[править | править код]
Эмиссионный спектр[править | править код]
Квантование энергии атомов проявляется в их спектрах поглощения (абсорбиционные спектры) и испускания (эмиссионные спектры). Атомные спектры имеют линейчатый характер (рис. 2).

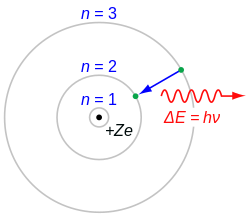
Возникновение линий в спектре обусловлено тем, что при возбуждении атомов электроны, принимая соответствующую порцию энергии, переходят на более высокий энергетический уровень. Переход электронов в состояние с более низким энергетическим уровнем сопровождается выделением кванта энергии (рис. 3).
Наиболее простой спектр у атома водорода, линии которого образуют спектральные серии; их положение описывается выражением ν = R (1/n12 — 1/n22), где ν — волновое число линии, R — постоянная Ридберга, n — целые числа, причём n2 > n1.
| Спектральные серии водорода | Переход на квантовый уровень n1 | Область спектра |
|---|---|---|
| Серия Лаймана | 1 | ультрафиолетовый |
| Серия Бальмера | 2 | видимый свет |
| Серия Пашена | 3 | инфракрасный |
| Серия Брэккета | 4 | далёкий инфракрасный |
| Серия Пфунда | 5 | --- |
| Серия Хэмпфри | 6 | --- |
Аналогичные серии наблюдаются в спектрах водородоподобных ионов (например, He+, Li2+). С увеличением числа электронов атомные спектры усложняются и закономерности в расположении линий становятся менее выраженными.
Поляризуемость атомов и молекул[править | править код]

Внешнее электрическое поле напряжённостью , наложенное на систему взаимодействующих ядер и электронов (атомов, ионов, молекул), деформирует её, вызывая появление наведённого дипольного момента где коэффициент имеет размерность объёма и является количественной мерой электронной поляризуемости (его также называют электронной поляризуемостью). На рис. 4 представлена деформационная поляризация (смещение электронной оболочки) атома водорода под действием электрического поля протона. При снятии внешнего электрического поля наведённый дипольный момент исчезает. В случае взаимодействия атома водорода и протона имеет место образование молекулярного иона водорода с простейшей одноэлектронной химической связью:
- 61 ккал/моль.
Относительно недавно были получены достоверные данные по электронным поляризуемостям большинства атомов в свободном состоянии. Наибольшее значение электронной поляризуемости наблюдается у атомов щелочных металлов, а минимальное — у атомов инертных газов[12].
В случае многоядерных систем внешнее электрическое поле приводит как к деформации электронных оболочек, так и изменению равновесных расстояний между ядрами (длины связи). В соответствии с этим поляризуемость молекулы составляется из двух слагаемых: где электронная поляризуемость, атомная поляризуемость[13].
Ионизация атомов и молекул[править | править код]
При высокой напряжённости внешнего электрического поля, наложенного на систему взаимодействующих ядер и электронов происходит её ионизация — отрыв электрона от атома или молекулы и образование положительно заряженного иона — катиона. Процесс образования ионов из атомов или молекул всегда эндотермический. Количество энергии, необходимое для отрыва электрона от возбуждаемых атомов или молекул, принято называть энергией ионизации. Для многоэлектронных атомов энергия ионизации l1, l2, l3… соответствует отрыву первого, второго, третьего и т. д. электронов. При этом всегда l1 < l2 < l3…, так как увеличение числа оторванных электронов приводит к возрастанию положительного заряда образующегося иона.
Наименьшей энергией ионизации (3—5 эВ) обладают атомы щелочных металлов, имеющих по одному валентному электрону, наибольшей — атомы инертных газов, обладающих замкнутой электронной оболочкой.
В связи с низкими значениями энергии ионизации щелочных металлов атомы их под влиянием различных воздействий сравнительно легко теряют свои внешние электроны. Такая потеря происходит под действием освещения чистой поверхности щелочного металла. На этом явлении, которое носит название фотоэлектрического эффекта, основано действие фотоэлементов, то есть приборов, непосредственно трансформирующих световую энергию в электрическую[14]. Квантовая природа фотоэлектрического эффекта установлена Эйнштейном, которому присуждена в 1921 году Нобелевская премия за труды по теоретической физике, особенно за открытие законов фотоэффекта.
Сродство к электрону[править | править код]


Электрон, обладая отрицательным элементарным зарядом 1,602•10−19 Кл, как и всякий точечный электрический заряд создаёт вокруг себя электрическое поле с напряжённостью где расстояние точки поля до электрона. Атом водорода, попадая в электрическое поле электрона, подвергается деформационной поляризации. Величина наведённого дипольного момента μ, прямо пропорциональна напряжённости электрического поля
Величина смещения центра электронной оболочки атома водорода обратно пропорциональна квадрату расстояния атома водорода к приближающемуся электрону (рис. 5). Сближение атома водорода и электрона возможно до тех пор, пока центры областей плотностей вероятности нахождения электронов не станут равноудалёнными от ядра объединённой системы — отрицательно заряженного иона водорода (гидрид-иона ).
Энергетический эффект процесса присоединения электрона к нейтральному атому Э принято называть энергией сродства к электрону. В процессе присоединения электрона к нейтральному атому образуется отрицательно заряженный ион (анион) Э–:
- Э + e → Э–.
На рис. 6 представлена зависимость энергии сродства к электрону атомов от порядкового номера элемента для некоторых элементов. Наибольшим сродством к электрону обладают p-элементы VII группы (галогены).
Взаимодействие отдельных молекул[править | править код]
Межмолекулярное взаимодействие — это электромагнитное взаимодействие электронов и ядер одной молекулы с электронами и ядрами другой. Межмолекулярное взаимодействие зависит от расстояния R между молекулами и их взаимной ориентации и определяется потенциальной энергией. Энергия притяжения молекул может быть представлена в виде трёх составляющих: ориентационной Еор, индукционной Еинд, и дисперсионной Едисп.[15]
См. также[править | править код]
- Атомная орбиталь
- Вычислительная химия
- Волновая функция
- Квантовая биохимия
- Компьютерная химия
- Метод самосогласованного поля
- Метод Хартри — Фока
- Молекулярный ион водорода
- Одноэлектронная химическая связь
- Релятивистская квантовая химия
- Статистическая интерпретация волновой функции
- Теория функционала плотности
- Теория молекулярных орбиталей
- Электронная плотность
- Электронное облако
- Электронная поляризуемость
- QMC@Home
Примечания[править | править код]
- ↑ Химическая Энциклопедия, 1990, Т. 2, с. 365–367.
- ↑ Давтян О. К. Квантовая химия. — М.: Высшая школа, 1962. — 784 с. — стр. 5
- ↑ Атом — статья из Большой советской энциклопедии.
- ↑ [1] Архивная копия от 4 ноября 2015 на Wayback Machine, Atom//IUPAC Gold Book.
- ↑ Справочник химика / Т.1. — Л.-М.: Госхимиздат, 1962. — С. 321—324. — 1072 с.
- ↑ Химический энциклопедический словарь / гл. ред. И. Л. Кнунянц. — М.: Сов. энциклопедия, 1983. — С. 59. — 792 с.
- ↑ Даниэльс Ф., Олберти Р. Физическая химия. — М.: «Мир», 1978. — С. 387. — 646 с.
- ↑ Ахметов Н. С. Неорганическая химия. — 2-е изд., перераб. и доп. — М.: «Высшая школа», 1975. — С. 35—38. — 672 с.
- ↑ Шусторович Е. М. Химическая связь. Сущность и проблемы.. — Москва: «Наука», 1973. — С. 57—67. — 232 с.
- ↑ Полинг Л. Кекуле и химическая связь (книга "Теоретическая органическая химия") / под. ред. Р.Х.Фрейдлиной. — М.: Издательство иностранной литературы, 1963. — С. 7—16. — 366 с.
- ↑ Гиллеспи Р. Геометрия молекул. — М.: Мир, 1975. — 280 с.
- ↑ Потапов А. А. Деформационная поляризация. Поиск оптимальных моделей. — Новосибирск: «Наука», 2004. — С. 356—358. — 511 с.
- ↑ Справочник химика. — Л.-М.: Издательство химической литературы, 1962. — С. 384. — 1072 с.
- ↑ Некрасов Б. В. Курс неорганической химии. — 14-е. — М.: Издательство химической литературы, 1962. — С. 681. — 976 с.
- ↑ Химический энциклопедический словарь. Гл. ред. И. Л. Кнунянц.. — М.: Сов. энциклопедия, 1984. — С. 318. — 792 с.
Литература[править | править код]
- Химическая энциклопедия : [рус.] : в 5 т. / под ред. И. Л. Кнунянца. — М. : Советская энциклопедия, 1990. — Т. 2. — 671 с. — ISBN 5-85270-035-5.
- Кругляк Ю. А. Квантовая химия. Киев: 1963—1991. — Одесса: ТЭС, 2016. — ISBN 978-617-7337-54-5. — 665 с.
- Кругляк Ю. А. Квантовое моделирование в квантовой химии на квантовых компьютерах. — Одесса: ТЭС, 2020. — ISBN 978-617-7711-56-7. — 339 с.
- Абаренков И. В., Братцев В. Ф., Тулуб А. В. Начала квантовой химии. — М.: Высшая школа, 1989. — С. 303. — ISBN 5-06-000492-9.
- Степанов Н. Ф. Квантовая механика и квантовая химия. — М.: Мир, 2001. — С. 519. — ISBN 5-03-003414-5.
- Заградник Р., Полак Р. Основы квантовой химии. — М.: Мир, 1979. — 504 с.
- Грибов Л. А., Муштакова С. П. Квантовая химия. — М.: Гардарика, 1999. — 390 с.
- Жидомиров Г. М., Багатурьянц А. А., Абронин И. А. Прикладная квантовая химия. — М.: Химия, 1979. — 296 с.
- Татевский В. М. Квантовая механика и теория строения молекул. — М.: Изд-во МГУ, 1965. — 162 с.
- Бейдер Р. Атомы в молекулах. Квантовая теория. — М.: Мир, 2001. — 532 c. — ISBN 5-03-003363-7
- Цирельсон В. Г. Квантовая химия. Молекулы, молекулярные системы и твердые тела. Учебное пособие. М.: БИНОМ. Лаборатория знаний, 2010. — 495 с.
- Майер И. Избранные главы квантовой химии: доказательства теорем и вывод формул. — БИНОМ. Лаборатория знаний, 2006. — 384 с. — ISBN 5-94774-499-6
- Дмитриев И. С., Семенов С. Г. Квантовая химия — её прошлое и настоящее. Развитие электронных представлений о природе химической связи. — М.: Атомиздат, 1980. — 160 с.
- Эйринг Г. Уолтер Дж., Кимбалл Дж. Квантовая химия. Пер с англ. — ГИИЛ, 1948. — 528 с.
- Козман У. Введение в квантовую химию. — М.: ИИЛ, 1960. — 558 с.
- Давтян О. К. Квантовая химия. — М.: Высшая школа, 1962. — 784 с.
- Введение в квантовую химию. Пер с япон. Под ред. С. Нагакуры, Т. Накадзимы. — М.: Мир, 1982. — 264 с.
- Современная квантовая химия. В двух томах. Пер с англ. Под ред. О. Синаноглу. — М.: Мир, 1968.
- Локализация и делокализация в квантовой химии. Пер с англ. Под редакцией О. Шальве, Р. Додель, С. Дине, Ж.-П. Мальрье. — М.: Мир, 1978. — 412 с.
- Кругляк Ю. А., Уитмэн Д. Р. Таблицы интегралов квантовой химии. Том I, — М.: Вычислительный центр АН СССР, 1965. — 439 + XLV с.
- Кругляк Ю. А. Таблицы интегралов квантовой химии. Том II, — Харьков.: Харьковский государственный университет, 1966. — 179 с.
- Кругляк Ю. А., Квакуш В. С., Дядюша Г. Г., Хильченко В. И. Методы вычислений в квантовой химии. Расчет пи-электронной структуры молекул простыми методами молекулярных орбиталей. — Киев: Наукова думка, 1967. — 161 с.
- Кругляк Ю. А., Дядюша Г. Г., Куприевич В. А., Подольская Л. М.,Каган Г. И. Методы расчета электронной структуры и спектров молекул. — Киев: Наукова думка, 1969. — 307 с.
- Левин А. А. Введение в квантовую химию твердого тела. — М.: Химия, 1974. — 240 с.
- Дунген Х., Лыгин В. Квантовая химия адсорбции на поверхности твердых тел. Пер. с нем. — М.: Мир, 1980. — 288 с.
- Эварестов Р. А. Квантовохимические методы в теории твердого тела. — Л.: Изд-во ЛГУ, 1982. — 279 с.
- Бурштейн К. Я., Шорыгин П. П. Квантовохимические расчеты в органической химии и молекулярной спектроскопии. — М.: Наука, 1989.
- Хигаси К., Баба Х., Рембаум А. Квантовая органическая химия. Архивная копия от 4 марта 2016 на Wayback Machine Пер с англ. — М.: Мир, 1967. — 380 с.
- Минкин В. И., Симкин Б. Я., Миняев Р. М. Квантовая химия органических соединений. Механизмы реакций. — М.: Химия, 1986. — 248 с.
- Пюльман Б., Пюльман А. Квантовая биохимия. Перевод с англ. — М.: Мир, 1965. — 654 с.
- Ладик Я. Квантовая биохимия для химиков и биологов. Пер с нем. — М.: Мир, 1975. — 256 с.
- Голованов И. Б., Пискунов А. К., Сергеев Н. М. Элементарное введение в квантовую биохимию. — М.: Наука, 1969. — 236 с.
- Гельман Г. Г. Квантовая химия. — М.: ОНТИ, 1937. — 546 с.
- Гельман Г. Г. Квантовая химия М.: Бином. Лаборатория знаний, 2012. ISBN 978-5-94774-768-3
- Губанов В. А., Курмаев Э. З., Ивановский А. Л. Квантовая химия твердого тела. — М.: Наука, 1984. — С. 304.
- Mueller M. R. Fundamentals of Quantum Chemistry. Molecular Spectroscopy and Modern Electronic Structure Computations. — Kluwer, 2001. — pp. 265.
- Strategies and Applications in Quantum Chemistry. From Molecular Astrophysics to Molecular Engineering. Edited by Y. Ellinger, M. Defranceschi. — Kluwer, 2002. — pp. 461.
- Koch W., Holthausen M. C. A Chemist’s Guide to Density Functional Theory. 2-ed. — Wiley, 2001. — pp. 293.
Ссылки[править | править код]
- Сайт о квантовой химии Архивная копия от 3 апреля 2022 на Wayback Machine (создан при поддержке Уфимского квантовохимического общества)
- УДК 544.18 Квантовая химия Архивная копия от 2 декабря 2012 на Wayback Machine
- Квантовая химия в России Архивная копия от 19 января 2010 на Wayback Machine
- Область исследования 02.00.17 Математическая и квантовая химия Архивная копия от 4 марта 2016 на Wayback Machine
- Программа кандидатского экзамена по специальности 02.00.17 «Математическая и квантовая химия» с официального сайта Высшая аттестационная комиссия Министерства образования и науки Российской Федерации Архивная копия от 1 декабря 2018 на Wayback Machine
- Диссертационные советы по специальности 02.00.17 Математическая и квантовая химия
- Диссертационные работы по специальности Математическая и квантовая химия.















