Окружность девяти точек

Окружность девяти точек — это окружность, проходящая через середины всех трёх сторон треугольника.
Она также называется окружностью Эйлера, окружностью Фейербаха, окружностью шести точек, окружностью Теркема, окружностью n-точек, полуописанной окружностью.
Теорема-определение[править | править код]

Окружность девяти точек получила такое название благодаря следующей теореме:
- Основания трёх высот произвольного треугольника, середины трёх его сторон и середины трёх отрезков, соединяющих его вершины с ортоцентром, лежат все на одной окружности.
Иначе говоря, окружность девяти точек является описанной окружностью для следующих трёх треугольников:
- ортотреугольник,
- серединный треугольник,
- треугольник Эйлера (или треугольник Фейербаха, треугольник Эйлера — Фейербаха) — треугольник, вершинами которого служат середины трёх отрезков, соединяющих ортоцентр и вершины.
Доказательство теоремы[править | править код]
- В статье Лемма о трезубце приведено доказательство существования окружности Эйлера при помощи данной леммы.
Свойства[править | править код]
- Центр окружности девяти точек лежит на прямой Эйлера, точно в середине отрезка между ортоцентром и центром описанной окружности.

- Из девяти точек на окружности Эйлера три являются серединами отрезков, соединяющих вершины с ортоцентром (вершины треугольника Эйлера-Фейербаха). Эти три точки являются отражениями середин сторон треугольника относительно центра окружности девяти точек.
- Таким образом, центр девяти точек служит центром симметрии, переводящей серединный треугольник в треугольник Эйлера-Фейербаха (и наоборот)[1]
- Диаметр окружности девяти точек равен радиусу описанной окружности.
- Описанная окружность есть образ окружности девяти точек относительно гомотетии с центром в ортоцентре и коэффициентом 2.

- Последнее свойство гомотетичности (подобия) означает, что окружность девяти точек делит пополам любой отрезок, который соединяет ортоцентр с произвольной точкой, лежащей на описанной окружности.
- Теорема Фейербаха. Окружность девяти точек произвольного треугольника касается вписанной и всех трёх вневписанных окружностей этого треугольника.[2]
- Теорема Мавло.[3]: треугольник на своей окружности девяти точек отсекает внешним образом тремя своими сторонами три дуги таким образом, что длина наибольшей из них равна сумме длин двух оставшихся дуг. Например, на рисунке выше теорема Мавло дает равенство: дуга IF=дуга HE+дуга GD.
- В симметричном виде теорема Мавло может быть записана в виде:
- Это эквивалентно тому, что наибольшая из трех дуг равна сумме двух других.
- Последнее свойство — аналог свойств для расстояний , и от вершин дополнительного треугольника (треугольника с вершинами в серединах сторон данного треугольника). до точки Фейербаха, а не для дуг. Аналогичное соотношение также встречается в теореме Помпею.
- Теорема Гамильтона. Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих ту же самую окружность Эйлера (окружность девяти точек), что и исходный остроугольный треугольник. Точкой Фейербаха считается наиболее близкая к вершине A отмеченная жирно точка на окружности.

- На описанной окружности треугольника существуют ровно три точки, таких что их прямая Симсона касается окружности Эйлера треугольника , причем эти точки образуют правильный треугольник. Стороны этого треугольника параллельны сторонам треугольника Морлея.
- Если описанная около треугольника гипербола проходит через точку пересечения высот, то она равнобочная (то есть её асимптоты перпендикулярны)[4]. Точка пересечения асимптот равносторонней гиперболы лежит на окружности девяти точек[4]. Эта гипербола называется гиперболой Киперта, а её центр обозначен в энциклопедии центров треугольника как Х(115).
- Если прямая ℓ ортополюса проходит через центр описанной окружности треугольника, то сам ортополюс лежит на окружности Эйлера этого треугольника.[5]
- Если прямая ℓ ортополюса P проходит через ортоцентр Q треугольника, то точка, расположенная на продолжении отрезка PQ, соединяющего ортополюс с ортоцентром, по другую сторону на расстоянии, равном PQ, лежит на окружности Эйлера (на окружности 9 точек) этого треугольника.[6]
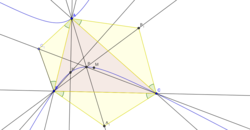
- Если ABCD — четырехугольник, вписанный в некоторую окружность. EFG — диагональный треугольник для четырехугольника ABCD. Тогда точка T пересечения бимедиан четырехугольника ABCD лежит на окружности девяти точек треугольника EFG.

- В работе[7] показано, что точка пересечения бимедиан четырехугольника, вписанного в некоторую окружность, принадлежит окружности Эйлера треугольника с одной вершиной в точке пересечения диагоналей четырехугольника и с двумя другими вершинами в точках пересечения продолжений его пар противоположных сторон.
- Для окружности девяти точек, которая — в числе прочих — носит и название «окружность Теркема», Теркем доказал теорему Теркема.[8] Она утверждает, что если окружность девяти точек пересекает стороны треугольника или их продолжения в 3 парах точек (в 3 основаниях соответственно высот и медиан), являющихся основаниями 3 пар чевиан, то, если 3 чевианы для 3 из этих оснований пересекаются в 1 точке (например 3 медианы пересекаются в 1 точке), то 3 чевианы для 3 других оснований также пересекаются в 1 точке (то есть 3 высоты также обязаны пересечься в 1 точке).
Случаи взаимного расположения окружности девяти точек и описанной окружности[править | править код]
В треугольнике по отношению к описанной окружности окружность девяти точек (или окружность Эйлера) может располагаться следующим образом:
- Она касается описанной окружности в единственном случае, если треугольник прямоугольный. При этом касание двух окружностей идет в вершине прямого угла треугольника.
- Она целиком лежит внутри описанной окружности, если треугольник остроугольный.
- Она пересекает описанную окружность в двух разных точках, если треугольник тупоугольный.
История[править | править код]
Эйлер в 1765 году доказал, что основания высот и середины сторон лежат на одной окружности (отсюда название «окружность шести точек»). Первое полное доказательство общего результата было, по-видимому, опубликовано Карлом Фейербахом в 1822 году (вместе с теоремой, носящей его имя), но есть указания на то, что оно было известно и ранее[2].
Вариации и обобщения[править | править код]
- Четыре окружности девяти точек треугольников внутри четырёхугольника. Известна теорема: В произвольном выпуклом четырёхугольнике окружности девяти точек треугольников , на которые его разбивают две диагонали, пересекаются в одной точке — в точке Понселе.[9]
- Известна теорема: Если в выпуклом четырёхугольнике перпендикулярны диагонали, то на одной окружности (окружность восьми точек четырёхугольника) лежат восемь точек: середины сторон и проекции середин сторон на противоположные стороны[10].

- Окружность девяти точек является частным случаем коники девяти точек. Если точка P — ортоцентр треугольника ABC, то коника девяти точек полного четырёхугольника PABC становится окружностью девяти точек.
- 16 окружностей Фейербаха, которых касается окружность 9 точек. На рисунке справа зелёным цветом показаны 16 известных окружностей Фейербаха, которые касаются окружности 9 точек, показанной красным цветом (сам треугольник показан чёрным цветом)

См. также (статьи, где упоминается окружность девяти точек)[править | править код]
- Геометрия треугольника
- Глоссарий планиметрии
- Замечательные точки треугольника
- Окружность
- Ортополюс
- Теорема Симсона
- Точка Понселе
- Отрезки и окружности, связанные с треугольником
- Список объектов, названных в честь Леонарда Эйлера
- Треугольник
- Центр девяти точек
- Четырёхугольник
- Энциклопедия центров треугольника
Примечания[править | править код]
- ↑ Dekov. Nine-point center// Journal of Computer-Generated Euclidean Geometry.— 2007.// http://eg-journal.comli.com/2007/JCGEG200721.pdf (недоступная ссылка)
- ↑ 1 2 Тони Крилли. Математика: 50 идей, о которых нужно знать = 50 Mathematical Ideas you really need to know. — Phantom Press. — 209 с. — ISBN 9785864716700. Архивировано 18 июня 2016 года.
- ↑ Д. П., Мавло (2004), "Красивые свойства замечательных тел", Математика в школi, Украина (№ 3): 265—269
- ↑ 1 2 Акопян А. В., Заславский А. А.. Геометрические свойства кривых второго порядка. — 2-е изд., дополн.. — М.: МЦНМО, 2011. — 148 с. — ISBN 978-5-94057-732-4.
- ↑ The Orthopole (21 января 2017). Дата обращения: 22 июня 2020. Архивировано 22 июня 2020 года.
- ↑ College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle. Nathan Altshiller-Court. (Параграф: G. The Orthopole. Пункт. 699. Теорема. Fig. 156. С.290-291). Mineola, New York: Dover Publication, Inc., 2012. 292 p.
- ↑ Fraivert, 2019.
- ↑ Дмитрий Ефремов. Новая геометрия треугольника Архивная копия от 25 февраля 2020 на Wayback Machine. — Одесса, 1902. — С. 16.
- ↑ Математика в задачах. Сборник материалов выездных школ команды Москвы на Всероссийскую математическую олимпиаду/ Под редакцией А. А. Заславского, Д. А. Пермякова, А. Б. Скопенкова, М. Б. Скопенкова и А. В. Шаповалова. c. 118, задача 9
- ↑ Математика в задачах. Сборник материалов выездных школ команды Москвы на Всероссийскую математическую олимпиаду/ Под редакцией А. А. Заславского, Д. А. Пермякова, А. Б. Скопенкова, М. Б. Скопенкова и А. В. Шаповалова. c. 118, задача 11
Литература[править | править код]
- Шарыгин И., Ягубьянц А. Окружность девяти точек и прямая Эйлера // Квант. — 1981. — № 8. — С. 34—37.
- Дм. Ефремов. Новая геометрия треугольника 1902 год
- Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).
- Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 48-50. — ISBN 5-94057-170-0.
- Feuerbach, Karl (1822), Eigenschaften einiger merkwürdigen Punkte des geradlinigen Dreiecks und mehrerer durch sie bestimmten Linien und Figurenнем.
- Мавло Д. П. Красивые свойства замечательных тел//Математика в школi. № 3, 2004. с. 265—269.
- Dekov. Nine-point center // Journal of Computer-Generated Euclidean Geometry. — 2007.
- Fraivert David. New points that belong to the nine-point circle // The Mathematical Gazette. — 2019. — Т. 103, № 557. — С. 222-232.









