Гиперпрямоугольник

Гиперпрямоугольник n-прямоугольник
Прямоугольный параллелепипед является 3-прямоугольником
Тип	Призма
Фасет	2n
Вершин	2n
Символ Шлефли	{} × {} … × {}
Диаграмма Коксетера — Дынкина	…
Группа симметрии	[2n-1], порядок 2n
Двойственный многогранник	Прямоугольный n-ромб
Свойства	выпуклый, зоноэдр, изогональный

n-гиперпрямоугольник — это обобщение прямоугольника на более высокие размерности и формально определяется как прямое произведение промежутков.

Типы

Трёхмерный гиперпрямоугольник называется также прямоугольной призмой или прямоугольным параллелепипедом.

Специальный случай n-прямоугольника, в котором все рёбра имеют одинаковую длину, является n-кубом.

По аналогии термин «гиперпрямоугольник» относится к прямому произведению ортогональных интервалов другого вида, таких как диапазоны ключей в базе данных или диапазоны целых чисел, а не вещественных чисел.

Двойственный многогранник

n-ромб
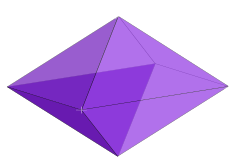Пример: 3-ромб
Фасет	2n
Вершин	2n
Символ Шлефли	{} + {} + … + {}
Диаграмма Коксетера — Дынкина	…
Группа симметрии	[2n-1], порядок 2n
Двойственный многогранник	n-прямоугольник
Свойства	выпуклый, изогональный

Двойственный многогранник n-прямоугольника называется n-ортоплексом или n-ромбом. Многогранник строится по 2n точкам в центрах прямоугольных фасет прямоугольника.

Символ Шлефли n-ромба представляется суммой n ортогональных отрезков: { } + { } + … + { }.

1-ромб — это отрезок. 2-ромб — это ромб.

n	Пример
1	{ }
2	{ } + { }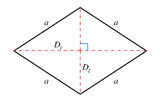
3	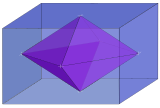Ромбический 3-ортоплекс внутри 3-прямоугольника { } + { } + { }

См. также

• Минимальный ограничивающий параллелепипед

Литература

• Coxeter H. S. M.D. Regular Polytopes. — 3rd. — New York: Dover, 1973. — ISBN 0-486-61480-8.
• Yi Zhang, Kamesh Munagala, Jun Yang. Storing matrices on disk: Theory and practice revisited // Proc. VLDB. — 2011. — Т. 4, вып. 11. — С. 1075–1086.

Ссылки

• Weisstein, Eric W. Rectangular parallelepiped (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. Orthotope (англ.) на сайте Wolfram MathWorld.