Обменное взаимодействие

Слово «Взаимодействие» имеет и другие значения.

Обменное взаимодействие — взаимодействие тождественных частиц в квантовой механике, приводящее к зависимости значения энергии системы частиц от её полного спина. Представляет собой чисто квантовый эффект, исчезающий при предельном переходе к классической механике.

Исторические аспекты

Гейзенберг примерно в 1927 году

Понятие обменного взаимодействие напрямую связано с концепцией спина, которая разрабатывалась в конце 20-х годов XX века в работах Уленбека, Гаудсмита, Дирака, Паули, Гейзенберга и других. Концепция обмена возникла при изучении спектров излучения атома гелия, интерпретация которых была дана Гейзенбергом в 1926 году. Она объясняет существование двух «типов» гелия: орто- и парагелия, различающихся спиновой конфигурацией электронов. Молекула водорода была описана Вальтером Гайтлером и Фрицем Лондоном через год после гейзенберговской теории гелия. Они впервые показали роль обменного взаимодействия в химии. В том же 1927 году Гейзенберг описал ферромагнетизм. Дираком в 1929 был предложен модельный гамильтониан, содержащий скалярное произведение операторов спинов. Его модель была обобщена ван Флеком в 1932 году. Этим работам предшествовала модель, предложенная в 1920 году Вильгельмом Ленцем и позднее развитая его учеником Эрнстом Изингом (1925 год), в которой рассматривалась одномерная решётка спинов, которые могли ориентироваться только вдоль выбранного направления. Первоначально, она не получила признания, так как не объясняла явления ферромагнетизма, но к 40-м было показано, что она хорошо описывает магнетизм двухэлементных сплавов (1938 год — статья Ханса Бете) и может быть применена не только в магнетизме.

Дальнейшее развитие теории было связано с изучением внутренних механизмов обменного взаимодействия. В то время как первые работы были посвящены так называемому прямому обменному взаимодействию, которое реализуется через непосредственное перекрытие волновых функций соседних атомов, его реальный механизм может существенно отличаться в различных классах соединений. Обменное взаимодействие, возникающее иными способами, получило название косвенного. В 1950 году была предложена теория Хендрика Крамерса и Филипа Андерсона, объясняющая антиферромагнетизм соединений d-металлов типа оксида марганца. К середине 50-х появилась теория РККИ-обменного взаимодействия. Позднее было дано объяснение так называемого слабого ферромагнетизма, исходя из идеи анизотропных моделей.

В настоящее время развитие теории связано с необходимостью учёта обменного взаимодействия как наиболее сильного из магнитных взаимодействий и его ролью в теории спиновых волн.

Обменное взаимодействие бозонов и фермионов

Характер обменного взаимодействия между частицами с целым спином (бозонами) и полуцелым спином (фермионами) различен. Для фермионов характер обменного взаимодействия обусловлен принципом Паули, согласно которому два фермиона не могут находиться в совершенно одинаковых состояниях. Принцип Паули запрещает двум электронам с параллельными спинами находиться в перекрывающихся допустимых областях. Поэтому на малых расстояниях порядка длины волны де Бройля между электронами, спины которых параллельны, возникает как бы дополнительное отталкивание. В случае антипараллельных спинов возникают силы притяжения, которые играют важную роль при образовании химических связей между атомами. При образовании некоторых молекул, в частности воды и водорода, определённую роль играет обменное взаимодействие между протонами. Обменное взаимодействие характерно для всех фермионов и существует независимо от того, имеются ли между ними другие взаимодействия. Противоположный характер имеет обменное взаимодействие бозонов: чем больше бозонов находится в данном состоянии, тем с большей вероятностью в это состояние переходит ещё один бозон. Это равносильно эффекту притяжения бозонов.

Внутриатомное и межатомное обменное взаимодействие электронов

Симметричность волновых функций

Электронная и спиновая структура атома описывается уравнением Дирака. Однако для систем с несколькими электронами его анализ очень громоздкий, а качественная картина взаимодействий может быть получена из не зависящего от времени уравнения Паули. Оно является следствием дираковского уравнения при малых скоростях и фактически являет собой уравнение Шрёдингера с дополнительным слагаемым в гамильтониане, учитывающим наличие спина. Немагнитная часть гамильтониана является суммой кинетических энергий электронов и энергии кулоновского взаимодействия электронов с ядром и между собой:

${\mathcal {H}}_{e}=\sum _{i=1}^{N}\left({\frac {\mathbf {p} _{i}^{2}}{2m}}-{\frac {Ze^{2}}{4\pi \varepsilon _{0}|\mathbf {r} _{i}|}}\right)+\sum _{i<j}{\frac {e^{2}}{4\pi \varepsilon _{0}|\mathbf {r} _{i}-\mathbf {r} _{j}|}}.$

Здесь сумма берётся по N электронам, которые находятся в электростатическом поле ядра зарядом Z, $\mathbf {p} _{i}$ и $\mathbf {r} _{i}$ — импульс и радиус-вектор i-го электрона, $\varepsilon _{0}$ — диэлектрическая постоянная.

Спин входит в гамильтониан через учёт спин-орбитального взаимодействия. Последнее имеет релятивистскую природу, как и взаимодействие спинов электронов между собой. Релятивистские слагаемые в гамильтониане по своей величине пропорциональны степеням отношения скорости электрона к скорости света и могут быть опущены в первом приближении. Это позволяет разделить переменные и записать полную волновую функцию $\Psi$ как произведение координатной и спиновой частей. Для двухэлектронной системы её можно подать в виде

$\Psi (\mathbf {r} _{1},\mathbf {s} _{1},\mathbf {r} _{2},\mathbf {s} _{2})=\Phi (\mathbf {r} _{1},\mathbf {r} _{2})\sigma (\mathbf {s} _{1},\mathbf {s} _{2}).$

Здесь функция $\Phi (\mathbf {r} _{1},\mathbf {r} _{2})$ определяется только координатами электронов, а $\sigma (\mathbf {s} _{1},\mathbf {s} _{2})$ — их спинами. Так как гамильтониан является суммой гамильтонианов отдельных электронов, точно также должна факторизоваться волновая функция каждого из электронов (так называемая спин-орбиталь — орбиталь, в которую введён спин как ещё одна переменная):

$\psi (\mathbf {r} ,\mathbf {s} )=\phi (\mathbf {r} )\sigma (s_{z}),\quad \phi (\mathbf {r} )=R_{n,l}(r)Y_{l,m}(\theta ,\phi )$

где R_{n, l} — радиальная часть, Y_{l, m} — сферическая гармоника, $\sigma (s_{z})$ — часть волновой функции, зависящая от спина. В случае многих электронов связь между полной волновой функцией и отдельными спин-орбиталями даёт детерминант Слейтера.

Наиболее простой системой, в которой важную роль играет обменное взаимодействие, является двухэлектронная. Она реализуется в атоме гелия и молекуле водорода. Электроны — это фермионы, поэтому полная волновая функция должна быть антисимметричной по отношению к перестановке электронов:

$\Psi (\mathbf {r} _{1},\mathbf {s} _{1},\mathbf {r} _{2},\mathbf {s} _{2})=-\Psi (\mathbf {r} _{2},\mathbf {s} _{2},\mathbf {r} _{1},\mathbf {s} _{1}).$

Так как при этом антисимметричность может быть получена двумя способами: пространственная часть волновой функции симметрична, а спиновая — нет, или наоборот. Они являются линейными комбинациями соответствующих частей спин-орбиталей. Поэтому из принципа Паули следуют две возможные формы $\sigma (\mathbf {s} _{1},\mathbf {s} _{2})$:

$\sigma _{\text{as}}(\mathbf {s} _{1},\mathbf {s} _{2})={\frac {1}{\sqrt {2}}}\left(\sigma _{1}(s_{z1})\sigma _{2}(s_{z2})-\sigma _{1}(s_{z2})\sigma _{2}(s_{z1})\right),$

$\sigma _{\text{sym}}(\mathbf {s} _{1},\mathbf {s} _{2})=\left\lbrace {\begin{array}{l}\sigma _{1}(s_{z1})\sigma _{2}(s_{z1}),\\{\frac {1}{\sqrt {2}}}\left(\sigma _{1}(s_{z1})\sigma _{2}(s_{z2})+\sigma _{1}(s_{z2})\sigma _{2}(s_{z1})\right),\\\sigma _{1}(s_{z2})\chi _{2}(s_{z2}).\end{array}}\right.$

Асимметричная функция соответствует так называемому синглетному состоянию (полный спин равен нулю), а симметричная — триплетному (полный спин равен единице). Соответствующие пространственные волновые функции имеют вид

$\Phi _{\text{sym}}(\mathbf {r} _{1},\mathbf {r} _{2})={\frac {1}{\sqrt {2}}}(\phi _{1}(\mathbf {r} _{1})\phi _{2}(\mathbf {r} _{2})+\phi _{1}(\mathbf {r} _{2})\phi _{2}(\mathbf {r} _{1})),$

$\Phi _{\text{as}}(\mathbf {r} _{1},\mathbf {r} _{2})={\frac {1}{\sqrt {2}}}(\phi _{1}(\mathbf {r} _{1})\phi _{2}(\mathbf {r} _{2})-\phi _{1}(\mathbf {r} _{2})\phi _{2}(\mathbf {r} _{1})).$

В этих формулах запись $\phi _{i}(\mathbf {r} _{k})\sigma _{j}(s_{zm})$ означает, что электрон, находящийся в точке с радиус-вектором $\mathbf {r} _{k}$ и проекцией спина $s_{zm}$ имеет пространственную волновую функцию $\phi _{i}$ и спиновую функцию $\sigma _{j}$. Каждая из этих волновых функций должна быть нормирована на единицу.

• Двухэлектронные пространственные волновые функции разной симметрии
• 
  Симметричная волновая функция (связывающая орбиталь)
• 
  Антисимметричная волновая функция (разрыхляющая орбиталь)

Обменное взаимодействие электронов в атомах. Гелий

Не учитывающий релятивистские взаимодействия гамильтониан для гелия имеет вид

${\mathcal {H}}=\underbrace {{\frac {\mathbf {p} _{1}^{2}}{2m}}+{\frac {\mathbf {p} _{2}^{2}}{2m}}-{\frac {2e^{2}}{4\pi \varepsilon _{0}|\mathbf {r} _{1}|}}-{\frac {2e^{2}}{4\pi \varepsilon _{0}|\mathbf {r} _{2}|}}} _{{\mathcal {H}}_{0}}+\underbrace {\frac {e^{2}}{4\pi \varepsilon _{0}|\mathbf {r} _{1}-\mathbf {r} _{2}|}} _{{\mathcal {H}}_{1}}.$

Изучить энергетические уровни атома гелия можно с помощью теории возмущений. Не очень точные, но достаточно наглядные вычисления могут быть проведены, если в качестве невозмущённого гамильтониана взять ${\mathcal {H}}_{0}$, а поправки к нему ${\mathcal {H}}_{1}$. Гейзенбергом в его работе, посвящённой спектрам гелия, в качестве нулевого приближения был взят гамильтониан ${\mathcal {H}}_{0}+{\frac {e^{2}}{4\pi \varepsilon _{0}|\mathbf {r} _{2}|}}$, а в качестве поправки выбрано выражение ${\mathcal {H}}_{1}-{\frac {e^{2}}{4\pi \varepsilon _{0}|\mathbf {r} _{2}|}}$. Этот подход более точен количественно, но и более громоздкий в аналитических вычислениях. В основном состоянии оба электрона гелия находятся на 1s орбитали и вследствие принципа Паули обязаны иметь противоположные направления спинов. Так как их главное, орбитальное и магнитное квантовые числа n, l и m одинаковы, пространственная часть полной волновой функции должна быть симметрична. В таком случае основное состояние характеризуется волновой функцией

$\Psi _{\text{gr}}(\mathbf {r} _{1},\mathbf {r} _{2},s_{1z},s_{2z})={\frac {1}{2}}\left(\phi _{100}^{(1)}(\mathbf {r} _{1})\phi _{100}^{(2)}(\mathbf {r} _{2})+\phi _{100}^{(1)}(\mathbf {r} _{2})\phi _{100}^{(2)}(\mathbf {r} _{1})\right)\left(\sigma _{1}(s_{z1})\sigma _{2}(s_{z2})-\sigma _{1}(s_{z2})\sigma _{2}(s_{z1})\right),$

где верхний индекс ψ нумерует электрон, а нижний обозначает тройку чисел $nlm=100$. Таким образом, энергия основного состояния равна

$E_{\text{gr}}=E_{0}+E_{1},$

где E₀ является собственным числом оператора ${\mathcal {H}}_{0}$ и находится из уравнения ${\mathcal {H}}_{0}\Psi _{\text{gr}}=E_{0}\Psi _{\text{gr}}$, а $E_{1}=\langle \Psi _{\text{gr}}|{\mathcal {H}}_{1}|\Psi _{\text{gr}}\rangle$.

Спектр гелия. Синглетному переходу с терма 2¹P₁ на 1¹S₀ соответствует яркая жёлтая линия (587 нм). Линии, соответствующие переходам с триплетного терма не видны вследствие их малой вероятности: основное состояние является синглетным, а электронные переходы со сменой мультиплетности запрещены правилами отбора.

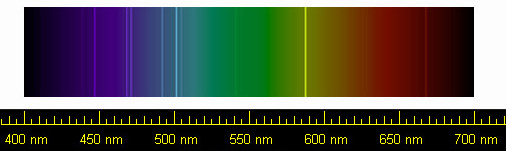
Природа обменного взаимодействия проявляется при исследовании возбуждённых уровней гелия. Обменное взаимодействие приводит к наличию расщепления энергетических уровней, при котором энергии состояний с занятыми орбиталями 1s2s и 1s2p различны. Возбуждённые уровни могут быть синглетными (парагелий) и триплетными (ортогелий) с волновыми функциями вида

$\Psi _{\text{es}}^{\text{S}}(\mathbf {r} _{1},\mathbf {r} _{2},\mathbf {s} _{1},\mathbf {s} _{2})=\Phi _{\text{sym}}(\mathbf {r} _{1},\mathbf {r} _{2})\sigma _{\text{as}}(\mathbf {s} _{1},\mathbf {s} _{2}),$

$\Psi _{\text{es}}^{\text{T}}(\mathbf {r} _{1},\mathbf {r} _{2},\mathbf {s} _{1},\mathbf {s} _{2})=\Phi _{\text{as}}(\mathbf {r} _{1},\mathbf {r} _{2})\sigma _{\text{sym}}(\mathbf {s} _{1},\mathbf {s} _{2})$

соответственно. Соответствующие им энергии возбуждённых состояний в первом порядке теории возмущений имеют вид

$E_{\text{es}}^{\text{S}}=\langle \Psi _{\text{es}}^{\text{S}}|{\mathcal {H}}_{1}|\Psi _{\text{es}}^{\text{S}}\rangle =K+J,$

$E_{\text{es}}^{\text{T}}=\langle \Psi _{\text{es}}^{\text{T}}|{\mathcal {H}}_{1}|\Psi _{\text{es}}^{\text{T}}\rangle =K-J.$

При таком вычислении энергии возбуждённых состояний роль спина сводится к наложению условия на симметричность пространственной части волновой функции. Это приводит к тому, что разница энергий синглетного и триплетного состояний составляет величину 2J. Здесь

$K=\iint |\phi _{100}(\mathbf {r} _{1})|^{2}{\frac {e^{2}}{4\pi \varepsilon _{0}|\mathbf {r} _{1}-\mathbf {r} _{2}|}}|\phi _{nlm}(\mathbf {r} _{2})|^{2}\mathrm {d} \mathbf {r} _{1}\mathrm {d} \mathbf {r} _{2}$

называется кулоновским интегралом, а

$J=\iint \phi _{100}(\mathbf {r} _{1})\phi _{nlm}(\mathbf {r} _{2}){\frac {e^{2}}{4\pi \varepsilon _{0}|\mathbf {r} _{1}-\mathbf {r} _{2}|}}\phi _{100}^{*}(\mathbf {r} _{2})\phi _{nlm}^{*}(\mathbf {r} _{1})\mathrm {d} \mathbf {r} _{1}\mathrm {d} \mathbf {r} _{2}$

обменным интегралом (звёздочка обозначает комплексное сопряжение). Кулоновский интеграл показывает силу электростатического отталкивания между плотностями вероятностей электронов и он всегда положительный. Обменный интеграл соответствует изменению энергии при изменении квантовых состояний электронов. Он может быть как положительным, так и отрицательным. Для гелия $J>0$, вследствие чего энергия синглетного состояния становится выше. Физический смысл этого состоит в том, что симметричная пространственная волновая функция располагает электроны ближе друг к другу и энергия кулоновского взаимодействия между ними увеличивается.

В действительности, вероятность наблюдения синглетного перехода 2¹P₁ → 1¹S₀ намного выше, чем вероятность наблюдать возбуждение электронов на триплетный уровень с меньшей энергией. Это связано с тем, что из-за слабости спинового взаимодействия переходы между энергетическими уровнями разной мультиплетности запрещены. Получить ортогелий с триплетной волновой функцией и спином, равным единице, можно бомбардируя парагелий электронным пучком. Так как в пучке есть электроны с различными направлениями спина, один из электронов в атоме гелия может быть выбит и замещён электроном, чей спин противоположен спину выбитого. Так как возвращение в основное состояние связано со сменой мультиплетности, оно маловероятно и время жизни ортогелия достаточно велико

Обменное взаимодействие в магнетиках

Модели с Гейзенберговским гамильтонианом

Модель Гейзенберга

Для описания ферромагнитного или антиферромагнитного упорядочивания в различных математических моделях обычно используют выражение энергии обменного взаимодействия спинов, предложенного Дираком, в котором энергия пропорциональна скалярному произведению операторов спинов s₁ и s₂

${\mathcal {H}}^{12}=-J_{12}\mathbf {s} _{1}\mathbf {s} _{2},$ (ГейзГам)

где $J_{12}$ — обменный интеграл. Его знак определяет тип взаимодействия: $J>0$ описывает ферромагнитное упорядочивание, а $J<0$ — антиферромагнитное. Выражение (ГейзГам) называют гамильтонианом Гейзенберга. Большинство магнетиков достаточно хорошо им описываются, однако в ряде случаев необходимо учитывать отличие реального гамильтониана от гейзенберговского. В простейшем случае он содержит только первую степень скалярного произведения, что соответствует спину $s=1/2$ (одноэлектронный ион), иначе необходимо учитывать слагаемые со степенями вплоть до 2s (многоэлектронные ионы). Случай, когда присутствует квадратичная поправка $J_{ij}'\cdot (\mathbf {s} _{1}\mathbf {s} _{2})^{2}$, называют биквадратным обменом. Она достигает минимума, когда спины перпендикулярны друг другу. Подобная связь между спинами может наблюдаться в многослойных системах.

Так как гамильтониан макроскопического тела, учитывающий кинетические энергии и энергии кулоновского взаимодействия ионов и электронов, имеет слишком сложную структуру для аналитического анализа, обычно предполагают что его можно заменить суммой гамильтонианов вида (ГейзГам). В таком случае обменный гамильтониан принимает вид

${\mathcal {H}}=-{\frac {1}{2}}\sum _{i\neq j}J_{ij}\mathbf {s} _{i}\mathbf {s} _{j},$

где сумма берётся по узлам решётки. Его иногда также называют гамильтонианом Гейзенберга—Дирака—ван Флека.. Во многих случаях можно считать, что обменный интеграл J быстро спадает с расстоянием и отличен от нуля только для соседних узлов магнитной подрешётки. Учёт более дальних соседей приводит к более сложному упорядочиванию спинов: геликоидальному, неколлинеарному и другим. Обменный гамильтониан Гейзенберга является изотропным и не определяет направления суммарной намагниченности системы. Он коммутирует с каждой из проекций суммарного спина S:

$[{\mathcal {H}},\mathbf {S} ]=0.$

Поэтому обменное взаимодействие не может влиять на величину полного спина системы.

В случае спиновой природы магнитного момента ферромагнетика можно перейти от оператора спина к оператору плотности магнитного момента через дельта-функцию Дирака δ:

$\mathbf {M} (\mathbf {r} )=-g\mu _{B}\sum _{i}\mathbf {s} _{i}\delta (\mathbf {r} -\mathbf {r} _{i}),$

где g — множитель Ланде, $\mu _{B}$ — магнетон Бора. Тогда можно записать макроскопическую энергию, соответствующую обменному гамильтониану, как

$E^{\text{ex}}=-{\frac {1}{2(g\mu _{B})^{2}}}\int _{V}\mathrm {d} \mathbf {r} \int _{V}'\mathrm {d} \mathbf {r} '{\overline {J}}(\mathbf {r} -\mathbf {r} ')\mathbf {M} (\mathbf {r} )\mathbf {M} (\mathbf {r} '),$

где функция ${\overline {J}}$ мало отличается от обменного интеграла при температурах, далёких от точки Кюри. Разложение намагниченности в ряд Тейлора позволяет выделить две составляющие макроскопической обменной энергии, одна из которых зависит только от модуля вектора намагниченности, а другая определяется его пространственными производными:

$w=-{\frac {1}{2}}\Lambda \mathbf {M} ^{2}+{\frac {1}{2}}A_{ij}{\frac {\partial \mathbf {M} }{\partial x_{i}}}{\frac {\partial \mathbf {M} }{\partial x_{j}}},$

где

$\Lambda ={\frac {1}{(g\mu _{B})^{2}}}\int _{V}{\overline {J}}(\mathbf {r} )\mathrm {d} \mathbf {r} ,\quad A_{ij}={\frac {1}{2(g\mu _{B})^{2}}}\int _{V}{\overline {J}}(\mathbf {r} )x_{i}x_{j}\mathrm {d} \mathbf {r} .$

В этом выражении не учитываются поверхностные эффекты, вклад в которые могут давать нечётные степени в разложении функции M по степеням r. Они могут быть актуальны для пироэлектрических кристаллов. Порядок констант A и Λ определяется значением обменного интеграла J₀ для соседних атомов и постоянной магнитной решётки a. В простейшем случае их оценивают как $A_{ij}\sim J_{0}a^{5}/(2\mu _{B})^{2}$ и $\Lambda \sim J_{0}a^{3}/(2\mu _{B})^{2}$. Сам обменный интеграл соседних ионов равен

$J_{0}\approx 3kT_{C}/2Ns(s+1),$

где k — константа Больцмана, T_C — температура Кюри, а N — количество ближайших соседей (6 для кубической решётки). Для железа эта формула даёт значение 1,19⋅10⁻² эВ. Более точные оценки увеличивают это число на 40 %.

Модель Изинга и XY-модель

Основные статьи: Модель Изинга и XY-модель

В 1920 году Вильгельм Ленц предложил идею элементарных спиновых диполей, которые могут ориентироваться в строго определённых направлениях. Одномерная модель такой системы была развита в кандидатской диссертации его студента Эрнста Изинга, рассмотревшего гамильтониан в виде

${\mathcal {H}}^{\text{Ising}}=-\sum _{i,j}J_{ij}s_{i}s_{j}-\sum _{i}H_{i}s_{i},$.

где $s_{i}=\pm 1$ — спины единичной длины, взаимодействие которых определяется величиной $J_{ij}$, H_i — магнитное поле в месте расположения i-го спина. Эта одна из простейших физических моделей, где объекты принимают лишь два значения (в данном случае проекции спина вверх или вниз), также нашла применение за пределами теоретической физики: в пожаротушении, политике и других областях. В магнетизме её можно рассматривать как предельный случай сильной лёгкоосной анизотропии, когда отклонениями от направления лёгкой оси можно пренебречь.

Первоначально, рассмотренная Изингом модель магнетика не вызвала интереса, так как в ней отсутствовало ферромагнитное упорядочение при конечных температурах. Однако позднее Ханс Бете обнаружил, что она отлично описывает энергии связи и химические потенциалы между атомами в двухэлементных сплавах, что нашло применение в металлургии. Рудольф Пайерлс показал, что дальний порядок, необходимый для объяснения ферромагнетизма, присутствует при низких температурах, если рассматривать двух- и трёхмерные спиновые решётки. При этом в модели возникают фазовые переходы, соответствующие наличию температуры Кюри. Подробный математический анализ двумерных решёток был выполнен Онсагером в 1944 году. Двумерная модель может быть экспериментально реализована на монослоях ферромагнитных атомов. Температурная зависимость и зависимость спонтанной намагниченности монослоёв железа на подложке W (110) показали отличное согласие с теорией вблизи температуры Кюри.

Другой предельный случай (сильная лёгкоплоскостная анизотропия) рассматривается так называемой XY-моделью. В ней гамильтониан обычно представляется в виде

${\mathcal {H}}^{\text{XY}}=-\sum _{i,j}J_{ij}(s_{ix}s_{jx}+s_{iy}s_{jy}).$

В отличие от модели Изинга здесь предполагается, что все спины лежат в плоскости XY. Обе модели — XY и Изинга играют важную роль в статистической механике.

Анизотропные модели

Причина анизотропии

В многоэлектронных атомах становится важным взаимодействие спинового и механического моментов. LS-связь приводит к расщеплению спектра свободного атома и влиянию симметрии кристаллической решётки на спины в атомах твёрдого тела. В частности, вклад поля решётки превышает несколько энергетических единиц kT (k — константа Больцмана, T — температура) для элементов группы железа. Учёт поправок, вносимых спин-орбитальным взаимодействием и магнитным полем (внешним или решётки) во втором порядке теории возмущений приводит к дополнительному слагаемому в гамильтониане для узла решётки

$\Delta {\mathcal {H}}=\sum _{\mu \nu }[2\mu _{B}H_{\mu }(\delta _{\mu \nu }-\xi \Lambda _{\mu \nu })s_{\nu }-\xi ^{2}\Lambda _{\mu \nu }s_{\mu }s_{\nu }-\mu _{B}^{2}\Lambda _{\mu \nu }H_{\mu }H_{\nu }].$

где δ_μν — символ Кронекера, $\Lambda _{\mu \nu }=\sum _{n}{\frac {\langle n|L_{\mu }|0\rangle \langle 0|L_{\nu }|n\rangle }{E_{n}-E_{0}}}$, а индексы μ и ν пробегают пространственные координаты x, y, z. В нём первое слагаемое является зеемановской энергией (энергия взаимодействия с магнитным полем), второе слагаемое соответствует так называемой одноионной анизотропии, а третье является следствием теории возмущений второго порядка и даёт парамагнитную восприимчивость не зависимую от температуры (парамагнетизм ван Флека). При отсутствии внешних магнитных полей направление полного спина определяется магнитной анизотропией, которая имеет описанную спин-орбитальную природу Иногда её включают в обменный гамильтониан считая J тензором:

${\mathcal {H}}=-{\frac {1}{2}}\sum _{i\neq j}(J_{xx}\mathbf {s} _{i}^{x}\mathbf {s} _{j}^{x}+J_{yy}\mathbf {s} _{i}^{y}\mathbf {s} _{j}^{y}+J_{zz}\mathbf {s} _{i}^{z}\mathbf {s} _{j}^{z}).$

Это обобщение также называют X—Y—Z моделью. Разница между элементами тензора J обычно мала. В некоторых случаях (ГейзГам) может усложняться. Для ионов, чьё основное состояние мультипленое, в нём используется оператор полного момента J и соответствующий ему множитель Ланде g_J:

${\mathcal {H}}^{12}=-J_{12}(g_{J}-1)^{2}\mathbf {J} _{1}\mathbf {J} _{2}.$

Такая ситуация характерна для редкоземельных ионов. При наличии ионов с f-электронами, взаимодействие также становится анизотропным. Частными случаями этого являются псевдодипольное обменное взаимодействие и взаимодействие Дзялошинского — Мория.

Псевдодипольное и антисимметричное обменные взаимодействия

Анизотропные взаимодействия играют важную роль в объяснении свойств антиферромагнитных купратов. Возникновение специальных типов анизотропного обмена можно показать на примере двух магнитных ионов для которых малой поправкой к гамильтониану считаются сумма вкладов спин-орбитальных взаимодействий каждого из ионов и обменного взаимодействия между ионами. Третий порядок теории возмущений приводит к изменению невозмущённого гамильтониана на величину

$\Delta {\mathcal {H}}^{\text{an}}=-{\frac {1}{4}}\sum _{\mu \nu }\sum _{i=1,2}[(\Gamma _{\mu \nu }^{(i)}+\Gamma _{\nu \mu }^{(i)})-\delta _{\mu \nu }(\Gamma _{xx}^{(i)}+\Gamma _{yy}^{(i)}+\Gamma _{zz}^{(i)})]S_{1\mu }S_{2\nu },$

$\Gamma _{\mu \nu }^{(i)}=2\xi ^{2}\sum _{n_{i}n_{i}'}{\frac {\langle g_{1}|L_{\mu }|n_{1}\rangle J(n_{1}g_{2},n_{1}'g_{2})\langle n_{1}'|L_{\nu }|g_{1}\rangle }{(E_{n_{1}}-E_{g_{1}})(E_{n'_{1}}-E_{g_{1}})}}.$

Здесь g_i — основное состояние, а $J(n_{1}g_{2},n_{1}'g_{2})$ — константа обменного взаимодействия между ионами для соответствующих состояний кадого из них. С одной стороны эта поправка может рассматриваться как анизотропное обменное взаимодействие, а с другой — как обобщение обычного магнитодипольного. В связи с этим его называют псевдодипольным взаимодействием. По порядку величины его вклад в энергию пропорционален произведению обменной константы на квадрат анизотропной поправки к фактору Ланде.

Недиагональные члены поправки второго порядка в теории возмущений приводят к поправке вида

$E_{12}=\mathbf {D} [\mathbf {S} _{1}\times \mathbf {S} _{2}].$

Взаимодействие такого вида называют антисимметричным обменным взаимодействием или взаимодействием Дзялошинского — Мория. Вектор

$\mathbf {D} =-2i\xi \left[\sum _{n_{1}}{\frac {\langle g_{1}|L_{1}|n_{1}\rangle }{E_{n_{1}}-E_{g_{1}}}}J(n_{1}g_{2},g_{1}g_{2})-\sum _{n_{2}}{\frac {\langle g_{2}|L_{2}|n_{2}\rangle }{E_{n_{2}}-E_{g_{2}}}}J(n_{2}g_{1},g_{1}g_{2})\right]$

называют вектором Дзялошинского. Он равен нулю, если поле кристаллической решётки симметрично по отношению к инверсии относительно центра между обоими ионами. Очевидно, энергия взаимодействия ненулевая только если ячейки не магнитно эквивалентны. Взаимодействие Дзялошинского — Мория проявляется в некоторых антиферромагнетиках. Результатом является появление слабой спонтанной намагниченности. Этот эффект называют слабым ферромагнетизмом, так как результирующая намагниченность составляет десятые доли процента от намагниченности в типичных ферромагнетиках. Слабый ферромагнетизм проявляется в гематите, карбонатах кобальта, манганитах, ортоферритах и некоторых других металлов. Выраженный в радианах угол между магнитными подрешётками при слабом ферромагнетизме по порядку величины равен анизотропии множителя Ланде.

Косвенный обмен

Прямой и косвенный обмен

Обменная энергия это добавка к энергии системы взаимодействующих частиц в квантовой механике, обусловленная перекрытием волновых функций при ненулевом значении полного спина системы частиц. В случае непосредственного перекрытия двух волновых функций говорят о прямом обмене (Гейзенберга), а в случае присутствия частицы-посредника, через которую происходит взаимодействие, говорят о косвенном обмене. Посредниками при косвенном обмене могут выступать диамагнитные ионы (наподобие кислорода O²⁻) или электроны проводимости. Первый случай теоретически был рассмотрен Крамерсом (1934) и Андерсоном (1950-е), а второй был предсказан Рудерманом и Киттелем (1954). В реальных кристаллах, в той или иной мере присутствуют все типы обмена. Внутренний характер взаимодействия слабо влияет на описание макроскопических систем, так как выражение (ГейзГам) имеет общий характер, а конкретный тип обмена (косвенный или прямой), определяется аналитическим выражением для J₁₂.

Суперобменное взаимодействие

Схема суперобменного взаимодействия в антиферромагнетике

Большинство ферро- и ферримагнитных диэлектриков состоит из магнитных 3d-ионов, разделённых такими немагнитными ионами, как O²⁻, Br⁻, Cl⁻ и др. Образуется ситуация, когда расстояния для непосредственного взаимодействия 3d-орбиталей слишком велико и обменное взаимодействие осуществляется перекрытием волновых функций 3d-орбиталей магнитных ионов и p-орбиталей немагнитных ионов. Орбитали оказываются гибридизированными, а их электроны становятся общими для нескольких ионов. Такое взаимодействие называется суперобменным. Его знак (то есть, является ли диэлектрик ферро- или антиферромагнетиком) определяется типом d-орбиталей, количеством электронов на них и углом, под которым видна пара магнитных ионов из узла, где находится немагнитный ион.

Двойной обмен

Оксиды переходных металлов могут быть как проводниками, так и диэлектриками. В диэлектриках имеет место суперобменное взаимодействие. Однако управляя легированием можно добиться перехода оксида в проводящее состояние. В манганитах лантана вида La_1−xCa_xMnO₃ при определённых значениях параметра x про часть ионов марганца может иметь валентность 3+, а другая — 4+. Обменное взаимодействие между ними, совершаемое через ионы O^2-, называют двойным обменом. Эти соединения так же будут ферро- или антиферромагнетиками в зависимости от значения x. Ферромагнитное упорядочивание будет в том случае, если суммарные спины 3-х и 4-валентных ионов сонаправлены, при этом 4-й электрон может быть делокализован. Иначе он локализирован на ионе с меньшей валентностью. Для La_1−xSr_xMnO₃ переход из антиферромагнитной в ферромагнитную фазы происходит при $x\approx 0.1$ (бо́льшим значениям x соответствует ферромагнетик).

РККИ-обменное взаимодействие

Основная статья: РККИ-обменное взаимодействие

Редкоземельные элементы имеют частично заполненную 4f-орбиталь, характерный размер которой существенно меньше межатомных расстояний в кристаллической решётке. Поэтому 4f-электроны соседних ионов не могут напрямую взаимодействовать друг с другом. Обменное взаимодействие между ними осуществляется с помощью электронов проводимости. Каждый редкоземельный ион создаёт возле себя достаточно сильное эффективное поле, которое поляризует электроны проводимости. Такое косвенное обменное взаимодействие между 4f-электронами называют взаимодействием Рудермана — Киттеля — Касуя — Иосиды (РККИ-обменное взаимодействие). Будет ли металл ферро- или антиферромагнетиком зависит от строения 4f-зоны и расстояния между ионами Зависимость обменного интеграла от произведения волнового вектора электронов на уровне Ферми k_F и расстояния между магнитными ионами a $J(k_{F}a)$ имеет знакопеременный осциллирующий характер. Этим, в частности, объясняется существование геликоидальных и некоторых других магнитных структур. РККИ-взаимодействие существенно зависит от концентрации свободных носителей заряда и может быть существенно более дальнодействующим, чем прямой обмен.

Обменное взаимодействие в ядерной физике

Проявлениями обменного характера сильного взаимодействия являются обмен нуклонов при столкновениях электрическими зарядами, проекциями спинов и пространственными координатами, а также явление насыщения ядерных сил. Из-за действия обменных сил изотоп 5
2He является неустойчивым, так как один нуклон вследствие принципа Паули находится в $P$-состоянии, где обменные силы являются отталкивающими.

См. также

• Обменное смещение
• Метод самосогласованного (молекулярного) поля

Литература

1. Ахиезер А. И., Барьяхтар В. Г., Пелетминский С. В. Спиновые волны. — М.: Наука, 1967. — 368 с. — 10 000 экз.
2. Барьяхтар В. Г., Криворучко В. Н., Яблонский Д. А. Функции Грина в теории магнетизма. — К.: Наукова думка, 1984. — 336 с.
3. Блохинцев Д. И. Основы квантовой механики. — Изд. 5-е, перераб. — М.: Наука, 1976. — 664 с. — 34 000 экз.
4. Вонсовский С. В. Магнетизм. — М., 1971.
5. Ландау Л. Д., Лифшиц Е. М. «Теоретическая физика», в 10 т., т. 3 «Квантовая механика (нерелятивистская теория)», 5-е изд. стереотип., М., Физматлит, 2002, 808 с., ISBN 5-9221-0057-2 (т. 3) гл. 9 «Тождественность частиц», п. 62 «Обменное взаимодействие», с. 285—290.
6. de Lacheisserie É., Gignoux D., Schlenker M. Magnetism: Fundamentals. — Springer, 2005. — Vol. 1. — 507 p. — (Magnetism). — ISBN 9780387229676.
7. Stöhr, J. and Siegmann, H. C. Magnetism: From Fundamentals to Nanoscale Dynamics. — Springer-Verlag Berlin Heidelberg, 2006. — Vol. 152. — 820 p. — (Springer series in solid-state sciences). — ISBN 978-3540302827.
8. Mattis, D. C. The theory of magnetism made simple: an introduction to physical concepts and to some useful mathematical methods. — World Scientific, 2006. — 565 p. — ISBN 9789812385796.
9. Wolfgang Nolting, Anupuru Ramakanth. Quantum Theory of Magnetism. — Springer, 2009. — 752 p. — ISBN 9783540854159.
10. K. H. J. Buschow. Concise encyclopedia of magnetic and superconducting materials. — 2nd. — Elsevier, 2005. — P. 254. — 1339 p. — ISBN 9780080445861.
11. Kei Yosida. Theory of magnetism. — Springer, 1996. — 320 p. — ISBN 9783540606512.

Статьи

1. W. Heisenberg. Über die Spektra von Atomsystemen mit zwei Elektronen (нем.) // Zeitschrift für Physik : magazin. — 1926. — 26 October (Bd. 39). — S. 499—518. — doi:10.1007/BF01322090.
2. W. Heisenberg, P. Jordan. Anwendung der Quantenmechanik auf das Problem der anomalen Zeemaneffekte (нем.) // Zeitschrift für Physik : magazin. — 1926. — 16 March (Bd. 37). — S. 263—277. — doi:10.1007/BF01397100.
3. W. Heitler, F. London,. Wechselwirkung neutraler Atome und homöopolare Bindung nach der Quantenmechanik (нем.) // Zeitschrift für Physik : magazin. — 1927. — 30 June (Bd. 44). — S. 455—472. — doi:10.1007/BF01397394.

Ссылки

• Обменное взаимодействие в магнетизме — статья из Физической энциклопедии
• Обменное взаимодействие — Химическая энциклопедия