Спор о струне

Спор о струне, спор о колеблющейся струне, спор о звучащей струне — научная дискуссия, развернувшаяся в XVIII веке между крупнейшими учёными того времени вокруг изучения колебаний струны. В спор оказались вовлечены Д’Аламбер, Эйлер, Д. Бернулли, Лагранж. Дискуссия касалась определения понятия функции и оказала решающее влияние на множество разделов математики: теорию дифференциальных уравнений в частных производных, математический анализ и теорию функций вещественной переменной, теорию тригонометрических рядов Фурье и теорию обобщённых функций и пространств Соболева.
Предпосылки к спору[править | править код]

Возможность теоретического изучения колебаний с точки зрения механики появилась с открытием законов Ньютона (1687) и разработкой анализа бесконечно малых, интегрального и дифференциального исчислений. Однако различные исследования велись и до этого момента Галилеем, Мерсенном, Декартом, Гюйгенсом и др.[1] В 1625 году Мерсенном была обнаружена зависимость между частотой , натяжением , площадью поперечного сечения и длиной струны, выражающаяся в пропорциональности[2]
Закон Мерсенна был объяснен теоретически Тейлором почти через столетие, в 1713 году. В его работе исследуется отклонение струны от начального положения, выраженное в виде функции .
Тейлор полагал, что в любой фиксированный момент времени струна должна иметь форму синусоиды (что на самом деле оказывается простейшей формой колеблющейся струны)[2], амплитуда которой зависит от времени, и что при любом начальном условии струна стремится перейти в такое «основное» состояние (что, как оказалось, не соответствует действительности).[1] Этот подход, иногда называемый «методом стоячих волн», был продолжен Д. Бернулли, однако получил строгое обоснование лишь в работах Фурье.
Тейлор также установил, что сила натяжения, действующая на бесконечно-малый элемент струны и направленная в сторону её отклонения, пропорциональна второй производной . В дальнейшем Д’Аламбер стал рассматривать зависимость отклонения не только от пространственной координаты , но и от времени . Это позволило строго применить второй закон Ньютона, что, однако, потребовало переосмысления природы производной, рассматриваемой Тейлором: она стала частной производной . Ускорение элемента описывалось другой частной производной: .
В 1747 году Д’Аламбер переформулировал закон, найденный Тейлором, в терминах дифференциальных уравнений с частными производными и записал уравнение колебания струны в современном виде, называемом волновым уравнением:[2]
Решения Д’Аламбера и Эйлера[править | править код]


Д’Аламбер применяет следующий подход к решению уравнения колебания струны. Полагая , он заметил, что при выполнении уравнения колебаний струны справедливо равенство[3]
и сделал вывод, что коэффициент при дифференциальной форме является функцией от и может быть вычислен интегрированием правой части этого равенства. Это позволяет записать линейную систему на первые частные производные от , решение которой даёт полный дифференциал функции . Последняя восстанавливается повторным интегрированием. Этот метод позволяет записать решение уравнения колебания струны в виде
где и — некоторые произвольные функции, определяемые из начальных условий. Д’Аламбер назвал такое решение общим, подчёркивая, что оно представляет собой целое множество различных решений уравнения[4].
Аналогичное решение вскоре получил Эйлер, сформулировав то, что мы сейчас назвали бы задачей Коши с заданной начальной формой струны и нулевой начальной скоростью. Выведя уравнение колебания струны и рассматривая его для произвольного , он получил решение
незначительно отличающееся от решения Д’Аламбера.[5] В 1766 году Эйлер разрабатывает новый метод, известный сейчас как метод характеристик: переходя к координатам , он записывает исходное уравнение в виде[5]
который легко поддается интегрированию.
Несмотря на то, что Д’Аламбер и Эйлер получили практически одинаковые по форме решения уравнения колебания, они по-разному воспринимали их смысл. Ключевая проблема состояла в том, что полученные решения содержали произвольные функции. Однако общепринятого определения функции на тот момент не было, и среди математиков существовали разные мнения о том, какие функции допустимо рассматривать в анализе, а какие нет. Разногласия по этому вопросу между Д’Аламбером и Эйлером вылились в серию публикаций, начавших спор о струне, к которому впоследствии присоединились другие учёные.[6]
Определение функции[править | править код]

В зарождающемся математическом анализе XVII—XVIII веков присутствовали два основных подхода: наглядный нестрогий механико-геометрический и формальный алгебраический. С этих двух точек зрения воспринималось и понятие функции. С механистической точки зрения, восходящей к Ньютону и Барроу, функция — это переменная величина, изменяющаяся с течением времени. Последнее в данном случае выступает в качестве аргумента[7]. Другой подход к функции, восходящий к Ферма и Декарту, но впервые явно сформулированный Иоганном Бернулли (отцом Даниила Бернулли, о котором пойдёт речь ниже), состоит в том, что «функцией переменной величины… называется количество, составленное каким угодно способом из этой переменной величины и постоянных»[8], то есть некоторая формула, аналитическое выражение от аргумента (не обязательно являющееся аналитической функцией в современном понимании). Класс допустимых операций, с помощью которых можно было получать функции, также варьировался, однако обычно включал в себя арифметические действия, извлечение корня и переходы к пределам, что позволяло рассматривать бесконечные ряды[9][10]. Первый подход доставлял более широкий класс функций, однако ни строгого определения, ни эффективных методов работы со столь общим понятием функции к середине XVIII в. математики не имели[11], и в анализе, а также геометрических приложениях исследовались функции, задаваемые одной формулой[12].
Д’Аламбер рассматривал задачу о струне в первую очередь с позиции чистого математика и не считал своей целью объяснение таких физических эффектов, как гармоническое звучание струны или явление обертонов. Это может показаться несколько странным, но подобный подход к задачам, изначально происходящим из физики, оказался чрезвычайно эффективным в науке XVIII века[13][14]. Так, рассматривая колебание струны с закрепленными концами и нулевой начальной скоростью, Д’Аламбер записывает решение в виде
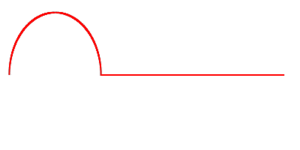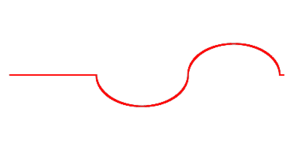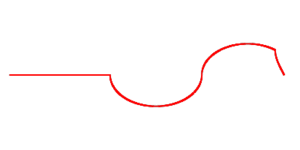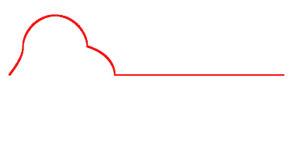
полагая при этом, что функция , определяющая положение струны в начальной момент времени, должна быть задана каким-то одним правилом, действующим для всех вещественных чисел (чтобы решение было определено для любого момента времени), но таким, чтобы она была нечётной и периодической, с периодом длины 2l (где l — длина струны), что требуется для выполнения граничных условий[13].
 |
| Начальное состояние струны, деформированной на небольшом интервале |
Для Эйлера, напротив, было понятно, что струне в начальный момент времени можно придать форму практически произвольной кривой, начерченной «свободным влечением руки»[6]. Из физических соображений он предложил рассмотреть функцию, определённую на интервале , а затем продолжить эту функцию, пользуясь её нечетностью и периодичностью, на все вещественные числа. Получившийся объект, однако, не был «функцией» в том смысле, который в него вкладывал Д’Аламбер (и даже сам Эйлер ранее)[15]. Впоследствии Эйлер предлагал также считать, что начальное условие (а, следовательно, и решение) может быть задано не одним аналитическим выражением, а несколькими («кусочно-аналитическое» задание), а впоследствии и вообще отказался от аналитического задания[6]. В частности, он допускал негладкие функции c «изломами» графика — которые естественно представить себе, рассматривая струну, оттянутую в одной точке[16].
 |
| Начальное состояние струны, оттянутой в одной точке |
Д’Аламбер отмечал, что рассматривать произвольную кривую нельзя, поскольку это «противоречит всем правилам анализа»[17], и настаивал на том, что начальное условие обязано задаваться одной периодической, нечетной и всюду дифференцируемой функцией[16]. Отдельной критике подверглось использование функций «с изломами». Д’Аламбер писал, что само уравнения колебания требует, чтобы решение имело как минимум вторые частные производные. Однако если начальное условие имело излом в какой-то точке, то и решение, получемое по найденным формулам, оказывалось негладким в какой-то момент времени в любой наперед заданной точке. Тем самым, оно не могло удовлетворять уравнению в точках изломов[16]. Здесь особую роль сыграло свойство гиперболических уравнений в частных производных (к которым относится уравнение колебания струны) сохранять гладкость начального условия, а не увеличивать её (что происходит в случае эллиптических уравнений)[18].
Основной ответ Эйлера на общие возражения состоял в том, что изучение уравнений с частными производными существенно отличается от «обычного анализа» функций одной переменной, где в основном рассматриваются преобразования отдельных аналитических выражений, и нет необходимости рассматривать «смешанные» функции[19]. Ответ на возражения по поводу негладких решений сводился к тому, что оно будет отличаться от гладкой лишь на «бесконечно-малую» величину, и это различие можно игнорировать — что, конечно, не могло устроить Д’Аламбера[16]. Другой аргумент состоял в том, что Эйлер предложил «забыть» об исходном уравнении, и считать, что явление описывается найденным общим решением, а не уравнением[20].
Взгляд физика: решение Д. Бернулли[править | править код]

Даниил Бернулли вступил в спор между Эйлером и Д’Аламбером, подвергнув критике их решения с точки зрения физики как чрезвычайно абстрактные. В своих публикациях он отмечал, что это замечательные математические результаты, но спрашивал: «при чём здесь звучащие струны?»[21].
Исходя из представлений о природе колебаний, он развивает идею о важной роли «чистых колебаний» синусоидальной формы, появившуюся ещё у Тейлора. Его догадка заключалась в том, что произвольное колебание может быть представлено как «наложение», или сумма, нескольких чистых колебаний (принцип суперпозиции), что соответствовало наблюдением за струной: издаваемый ею звук состоит из основного тона и множества обертонов. Бернулли нашёл решение уравнения колебания в виде суммы тригонометрического ряда и утверждал (опять же исходя из физических соображений), что таким рядом можно представить произвольную функцию. Это предположение он не мог подтвердить математически — в частности, он не знал формулы для вычисления коэффициентов такого ряда. Тем не менее он полагал, что его решение не только имеет бо́льший физический смысл, чем решения Д’Аламбера и Эйлера, но и является более общим[22].
В то время ряды были важным объектом изучения, и многие математики (включая Ньютона) рассматривали степенные ряды (с вещественными показателями степеней) как универсальный способ записи произвольных функций[23]. Однако необходимого уровня понимания тригонометрического ряда на тот момент достигнуто не было, и ни Д’Аламбер, ни Эйлер не согласились с тем, что тригонометрический ряд способен описывать достаточно широкий класс функций. Это непонимание усиливалось распространенным тогда представлением, что если два аналитических выражения совпадают на каком-то участке числовой оси, то они совпадают всюду. Так, Эйлер не мог поверить в то, что тригонометрическим рядом можно описать поведение струны, возмущённой только на небольшом участке. Возражения также вызывало требование периодичности функции, представимой в виде ряда, естественно следующее из периодичности слагаемых[24][25].
Лишь в много более поздних работах Фурье (начало XIX века) было показано, что даже недоступные для описания степенным рядом (и не являющиеся аналитическими в современном понимании) функции с изломами могут быть представлены на некотором отрезке тригонометрическим рядом. Дальнейшие исследования вопросов сходимости рядов Фурье привели Кантора к построению теории множеств и в конечном итоге к появлению современного функционального анализа[26].
Обобщённые функции[править | править код]
Результаты Фурье ответили на один из ключевых вопросов в споре о струне: о представимости широкого класса функций тригонометрическим рядом. Однако другой источник разногласий — парадокс, связанный с возможностью негладкости начальных условий, а, следовательно, и решений — оставался открытым не только в XVIII, но и в XIX веке. Он был разрешён только в XX веке с появлением аппарата обобщённых функций (распределений)[6]. Основы этой теории были заложены в конце 1936 года С. Л. Соболевым в результате исследования задачи Коши для гиперболических уравнений (к которым относится и уравнение колебания струны) и в дальнейшем строго развиты Лораном Шварцем в 1950-х годах[27].
Идея состоит в замене уравнения колебания на эквивалентное ему (в некотором смысле) интегральное уравнение, решение которого ищется уже не в классе дважды гладких функций, а в так называемых соболевских пространствах, представляющих собой пополнение пространства непрерывных функций по некоторой специальной метрике. Можно также считать, что производные негладкой функции, стоящие в левой части уравнения колебания струны, являются обобщённой функцией, и равенство справедливо в смысле обобщённых функций[28].
Примечания[править | править код]
- ↑ 1 2 Юшкевич 1972, с. 412.
- ↑ 1 2 3 Стиллвелл, с. 242
- ↑ Юшкевич 1972, с. 413
- ↑ Юшкевич 1972, с. 414
- ↑ 1 2 Юшкевич 1972, с. 415
- ↑ 1 2 3 4 Юшкевич 1972, с. 416
- ↑ Юшкевич 1970, с. 143—144
- ↑ Joh. Bernoulli, Opera omnia, v. II, Lausannae — Genevae, 1742, p. 241. Цит. по: Юшкевич 1970, с. 147
- ↑ Юшкевич 1970, с. 147
- ↑ Юшкевич 1972, с. 250
- ↑ Юшкевич 1970, с. 144
- ↑ Юшкевич 1972, с. 252
- ↑ 1 2 Ravetz, p. 75
- ↑ Christinsen, p. 36
- ↑ Ravetz, p. 76
- ↑ 1 2 3 4 Wheeler and Crummett, p. 35
- ↑ Kleiner, p. 287
- ↑ См. напр. Михайлов В. П. Дифференциальные уравнения в частных производных. — М.: Наука, 1976. — С. 35. — 391 с.
- ↑ Ravetz, p. 81
- ↑ Ravetz, p. 83
- ↑ Ravetz, p. 78
- ↑ Юшкевич 1972, с. 417—418
- ↑ Юшкевич 1972, 250—251
- ↑ Юшкевич 1972, с. 418
- ↑ Kleiner, p. 285
- ↑ Стиллвелл, с. 244—245
- ↑ См. напр. Кутателадзе С. С. Сергей Соболев и Лоран Шварц: Две судьбы, две славы // Сибирский журнал индустриальной математики. — 2008. — Т. 11, № 3. — С. 5—14. Архивировано 5 октября 2013 года.
- ↑ См. напр. Михайлов В. П. Дифференциальные уравнения в частных производных. — М.: Наука, 1976. — С. 266—298. — 391 с.
Литература[править | править код]
- История математики с древнейших времен до начала XIX столетия / Под ред. А. П. Юшкевича. — М.: Наука, 1970. — Т. II, математика XVII столетия. — 300 с.
- История математики с древнейших времен до начала XIX столетия / Под ред. А. П. Юшкевича. — М.: Наука, 1972. — Т. III, математика XVIII столетия. — 495 с.
- Стиллвелл, Дж. Математика и её история. — Ижевск: Институт компьютерных исследований/РХД, 2004. — 530 с.
- Wheeler, G. F., Crummett W. P. The vibrating string controversy // American Journal of Physics. — American Association of Physics Teachers, 1987. — Vol. 55, № 1. — P. 33—37. — doi:10.1119/1.15311.
- Christensen, T. Eighteenth-Century Science and the Corps Sonore: the Scientific Background to Rameau’s Principle of Harmony // Journal of Music Theory. — 1987. — Vol. 31. — P. 23—50.
- Ravetz J. R. Vibrating Strings and Arbitrary Functions // The Logic of Personal Knowledge: Essays Presented to M. Polanyi on his Seventieth Birthday. — London: Routledge, 1961. — P. 71—88.
- Kleiner, I. Evolution of the function concept: A brief survey // The College Mathematics Journal. — 1989. — Vol. 20. — P. 282—300.
- Ларин А. А. Зарождение математической физики и теории колебаний континуальных систем в «Споре о струне» // Вестник Национального технического университета «Харьковский политехнический институт». История науки и техники. — 2008. — № 8.
Эта статья входит в число хороших статей русскоязычного раздела Википедии. |