Количественный анализ экспрессии генов
Количественный анализ экспрессии генов — анализ транскриптома, измерение транскрипционной активности гена с помощью определения количества его продукта, матричной РНК (мРНК), универсальной для большей части генов.
При этом конечным продуктом экспрессии генов как правило являются белки, а не мРНК.
Методы[править | править код]
Методы для измерения количества мРНК :
- количественная ПЦР в реальном времени (qPCR) — из-за ограничений метода, применяют для анализа уровня экспрессии относительно небольшого количества генов
- сравнительная геномная гибридизация на чипах (CGH) — позволяет видеть количественные изменения экспрессии генов прямо на хромосомах
- микрочипы — можно получать данные по уровню экспрессии большого количества генов
- высокопроизводительное параллельное секвенирование РНК (RNA-Seq) — позволяет рассчитать количество как многочисленных, так и малочисленных РНК[1].
Количественный анализ экспрессии с помощью RNA-Seq[править | править код]
В результате секвенирования РНК создаётся библиотека ридов (или библиотека прочтений). Длина рида варьируется от 25 до 200 нуклеотидов в зависимости от выбранного метода секвенирования. После чего риды картируются (или выравниваются) на референсный геном. Риды могут быть выравнены сразу на несколько областей генома или на разные изоформы одного гена. Технология позволяет измерять лишь относительное количество транскрипта в клетке. Самый простой подход — рассматривать только однозначно выравненные риды на аннотированные модели генов. В этом случае величина RPKM[2] (reads per kilobase per million mapped reads — количество прочтений на килобазу на картированные риды) является подходящей количественной мерой экспрессии транскрипта[2]:
,
где — количество прочтений, попавших на транскрипт, — длина транскрипта, — общее количество прочтений. Эта формула является оценкой максимального правдоподобия при полиномиальной модели картирования ридов на транскрипты[3]
Однако многие прочтения не могут быть однозначно картированы. Например, при дупликациях гена, так как в таком случае не понятно, куда именно картировать геном. Также информация о структуре генов (альтернативный сплайсинг, альтернативные промоторы, разные сайты полиаденилирования) в высших эукариотах недостаточно изучена даже на модельных организмах, что также осложняет однозначное трактование полученных результатов. Поэтому используют подходы, позволяющие картирование с установлением точек сплайсинга[4] и последующей сборкой транскриптома[5].
В настоящее время существует большое разнообразие моделей для вычисления количества транскрипта. их можно разделить в зависимости от следующих основных свойств[6]:
- генеративная модель картирования ридов: используют полиномиальное, пуассоновское, отрицательное биномиальное, обобщённое пуассоновское. Известно, что генеративные модели вне зависимости от выбранного типа распределения приводят к одинаковым оценкам количества транскрипта[3].
- учитывающие «мульти-риды» (рид, который может относиться как к разным изоформам одного гена, так и к разным транскриптам разных генов).
- учитывающие парные риды (концы секвенированных фрагментов) — представляют ценную информацию, при их анализе необходимо оценивать распределение длин фрагментов. В случае парных ридов вводится мера FPKM (fragments per kilobase per million mapped reads — фрагменты на килобазу на миллион картированных прочтений)
- учитывающие систематические позиционные отклонения такие, как неравномерное покрытие транскрипта
- учитывающие систематические отклонения в зависимости от контекста последовательности такие, как концы ридов так, как они, как правило, неслучайны и означают предпочтения при фрагментации РНК.
В настоящее время существуют широкий спектр программ для количественного анализа экспрессии генов: Cufflinks[7], IsoEM, HTSeq, RSEM[8], MISO. Данные методы одинаково активно используются при оценки количества транскриптома, однако некоторые нюансы в работе заложенных алгоритмов могут сделать одну программу предпочтительней другой в зависимости от ситуации.
HTSeq[править | править код]
Простой подход, при котором считается количество ридов, которые пересекаются с данным геномом. При этом в программе заложены различные определения факта пересечения рида с геном. Далее экспрессию можно определять через RPKM[8].
Cufflinks[править | править код]
В данном алгоритме сначала происходит картирование библиотеки кДНК на геном для построения сплайсируемого выравнивания при помощи ещё одной программы TopHat. Затем на основании выравнивания строят граф с парными ридами кДНК в вершинах, где ребро проводится, если два парных рида могут находиться в одном транскрипте. На основании графа восстанавливаются возможные изоформы (как минимальное покрытие графа). В результате, риды картируются на построенные транскрипты. В рамках статистической модели, вероятность принадлежности рида изоформе пропорциональна количеству транскрипта, и на этом основании строится функция максимального правдоподобия, где максимум функции максимального правдоподобия отвечает искомому количеству транскриптов[5].
MISO[править | править код]
MISO (Mixture of Isoforms) представляет собой вероятностный фрэймворк, который количественно определяет уровень экспрессии альтернативно сплайсированных генов по данным RNA-Seq и идентифицирует дифференциально регулируемые изоформы или экзоны в образцах. В основе статистическая модель для оценки количества изоформ гена(MISO). MISO рассматривает уровень экспрессии набора изоформ как случайную переменную и оценивает распределение по значениям этой переменной. Алгоритм оценки основан на выборке и относится к методам Монте Карло по схеме марковской цепи («MCMC»).
Систематические ошибки и воспроизводимость[править | править код]
В результате секвенирования РНК происходят систематические ошибки, которые могут значительно влиять на оценку экспрессии. Многие биохимические особенности не удаётся обнаружить и учесть их влияние, однако, некоторые ошибки, такие как неслучайное и неравномерное по длине фрагментирование, всё же возможно учитывать до некоторой степени[9].
Для коррекции ошибок используют реплики. Существует два вида реплик: технические и биологические. Технические реплики предполагают секвенирование одного и того же биологического материала несколько раз. Биологические же реплики предполагают секвенирование различного биологического материала. Из отсеквенированных фрагментов прочитывается лишь небольшая часть. Часть ридов, относящихся к фиксированному гену, будет несколько отличаться для образца и небольшой рассматриваемой части ввиду случайного выбора этой части. Если часть ридов данного гена в образце равна p, то часть ридов, попавших на ген подчиняется биномиальному распределению или распределению Пуассона со средним p. Для оценки этой части p нужны технические реплики. В случае биологических реплик, вариация в экспрессии не объясняется распределением Пуассона. В этому случае используется отрицательное биномиальное или обобщённое пуассоновское распределения. При этом сохраняется допущение, что вариация зависит от среднего экспрессии. Ввиду малого количества биологических реплик, вариация оценивается с помощью различных регрессионных методов[10].
Анализ экспрессии генов с помощью ДНК-микрочипов[править | править код]
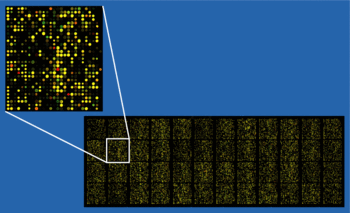
ДНК-микрочип представляет собой небольшую поверхность, на которую нанесены фрагменты одноцепочечной ДНК с известной последовательностью. Эти фрагменты выступают в роли зондов, с которыми гибридизуются комплементарные им цепи ДНК из исследуемого образца. Существует два различных типа ДНК-микрочипов — олигонуклеотидные микрочипы и кДНК-микрочипы[11].
С помощью кДНК-микрочипов удобно исследовать изменения в уровнях экспрессии генов в случаях, например, различных заболеваний. Из двух образцов клеток (контрольного и исследуемого) выделяется РНК, из которой обратной транскрипцией получают кДНК. Каждая из полученных проб окрашивается каким-либо красителем (обычно используются Cy3 и Cy5). Меченые образцы наносятся на микрочип одновременно, и после отмывки негибридизовавшихся молекул производится измерение флуоресценции с помощью сканирующего конфокального микроскопа[12].
При подготовке образца для анализа на олигонуклеотидном микрочипе на матрице полученной кДНК в присутствии метки (например, биотина или флюоресцеина) синтезируется кРНК. В условиях повышенной температуры меченая кРНК гибридизуется с зондами на микрочипе. Для нормализации, значения о связывании с мутированным олигонуклеотидом вычитаются из получившихся при анализе данных. Более того, поскольку для каждого гена создаётся примерно 25 различных зондов, итоговые значения для них высчитываются как среднее нормализованных интенсивностей всех этих проб[12].
Гибридизация на микрочипах, является очень сильным методом для одновременной оценки уровней экспрессии всех генов в исследуемом образце. Однако, природа данной техники исследования такова, что для получения достоверных качественных и количественных данных требуется аккуратный анализ полученных в эксперименте значений. Необходимо нормировать данные и максимально повысить соотношение сигнал/шум, поскольку изменения профилей экспрессии в сравниваемых образцах могут быть невелики[11].
Перед началом обработки данные представляют собой цифровое изображение интенсивностей флуоресценций различных каналов. В первую очередь проводится вычитание флуоресценции подложки из флуоресценции каждой конкретной пробы. Возможны два варианта — либо для каждой пробы высчитывается флуоресценция подложки непосредственно рядом с ней, либо считают среднюю флуоресценции подложки на всем микрочипе. Первый вариант считается более правильным, поскольку флуоресценция различных участком микрочипа может отличаться[12].
Вслед за вычитанием фона проводится нормировка интенсивностей флуоресценции красок. Флуоресценция красок и их слияние с зондами зависит от последовательности гена, условий проведения каждой конкретной гибридизации, качества микрочипа и от условий и длительности их хранения. Нормализацию проводят либо основываясь на флуоресценции проб, соответствующим генам домашнего хозяйства, либо внося на микрочип и в образец известное количество экзогенной, несвойственной исследуемым клеткам мРНК. Для получения более достоверных значений на разные области одного микрочипа наносятся одинаковые образцы ДНК. Индекс качества для микрочипа определяется уровнем различия значений данных для идентичных образцов в разных пробах[12].
Однако, несмотря на все это, получаемые в экспериментах данные не являются количественной оценкой экспрессии генов. Получаемые для одного гена результаты могут варьировать от лаборатории к лаборатории и от одного микрочипа к другому. Подобные эксперименты позволяют оценить качественные изменения профилей экспрессии в различных образцах[11].
Применение[править | править код]
Ранее учёные классифицировали различные типы рака основываясь лишь на том, какой орган был поражён. С помощью ДНК-микрочипов станет возможным классифицировать опухоли по паттернам активности генов в клетках. Это позволит разрабатывать лекарства, предназначенные для конкретного вида ракового заболевания. Кроме того, анализ профилей экспрессии в обработанных и необработанных лекарством клетках позволит учёным понять, как именно препарат влияет на клетки. Кроме того, зачастую в исследуемом образце опухоли присутствуют клетки разных клонов, которые могут значительно отличаться по профилю экспрессии генов. Оценка уровня экспрессии генов отдельных единичных клеток злокачественного новообразования позволит точнее прогнозировать дальнейшее развитие опухоли и её метастазов[13].
В лабораторных исследованиях методы количественного анализа экспрессии генов находят применение в ряде опытов, связанных с изучением экспрессий различных генов. В экспериментах, где клетки содержались в каких-либо условиях, отличных от нормальных, в большинстве своём обнаруживаются изменения в профилях экспрессии генов. Результаты подобных исследований проливают свет на механизмы клеточного ответа на изменения окружающей среды. Также уровни экспрессии генов активно меняются в ходе эмбрионального и постэмбрионального развитий, когда на смену одним белкам приходят другие, регулирующие процессы роста и формирования организма. Совместные изменения уровней экспрессии нескольких генов при смене каких-либо параметров могут говорить о взаимодействии продуктов этих генов в клетке[13].
Анализ экспрессии генов[править | править код]
Количественный анализ экспрессии генов проводится на нескольких уровнях и с разными целями[14],[15]:
1) Определение изменении экспрессии отдельного гена в зависимости от условий эксперимента (обработки образца).
2) Кластерный анализ генов по общей функциональности, взаимодействию, совместной регуляции. В данном случае используют методы сокращения размерности и методы визуализации. Как пример: метод главных компонент и кластеризация. Анализируют последовательности ДНК для нахождения регуляторных районов, мотивов.
3) Выявление и понимание сетей взаимодействия генов и белков, отвечающих наблюдаемым результатам измерения.
Таким образом, анализ изменения экспрессии можно рассматривать как кластеризацию генов на «изменившиеся» и «неизменившиеся»[14].
Систематические ошибки и воспроизводимость[править | править код]
Анализ изменения экспрессии генов может осложняться из-за плохой воспроизводимости, возникающей из-за большого количества сложно взаимосвязанных факторов, взаимодействующих на разных уровнях и на различных этапах эксперимента. Все вариации можно разделить на биологические, экспериментальные и технические источники вариации. К техническим источником вариций в полученных результатах относят: погрешность при изготовлении микрочипов, различия в технологиях получения и обработки изображения, способов выделения сигналов и обработки данных[15].
Биологические[править | править код]
Считается, что наибольший вклад во возникновение вариаций вносят различия индивидуальных уровней экспрессии генов в различных клетках и популяциях клеток. Различия обнаруживают не только между клиническими образцами (содержащими клетки различных типов), но даже между образцами моноклональных «идентичных» культур, являющиеся клонами одной клетки и содержащихся в «идентичных» условиях встречаются различия. Эти различия объясняются влиянием микроокружения (например, не совсем равномерным содержанием питательных веществ, градиентом температуры), различиями в фазе роста клеток в культуре, периодами быстрого изменения экспрессии генов и многими другими случайными воздействиями, неподдающимися контролю, такими как влияние клеток друг на друга и случайное распределение небольшого количества молекул транскрипционных факторов (экспрессия определённых генов может существенно зависеть от нескольких молекул)[15].
Так же на сохранность РНК влияет наличие вторичной структуры транскрипта[15].
Экспериментальные (подготовка образца)[править | править код]
Существенное значение имеет стандартизация всех этапов подготовки образцов (например, изменение температурного режима, состава питательных веществ даже при кратковременном центрифугировании живых клеток может вызвать изменение профиля экспрессии)[15]. Для подготовки образцов бактерий важное значение имеет быстрая деградация РНК в присутствии РНКаз, и в связи с эти следует соблюдать абсолютную стерильность, чтобы избежать превдевременной деградации РНК.
Наилучшей стратегией подготовки образца мРНК считают минимальное время обработки при условиях, «замораживающих» уровень мРНК на уровне в момент взятия образца, и ингибирование активности РНКаз[15], ферментов, разрушающих РНК[15].
Нормализация[править | править код]
При сравнении профилей экспрессии генов образцов применяют нормализацию, учитывающую источники экспериментальной и биологической вариации[16]:
- количество клеток в образце
- общую эффективность выделения РНК
- эффективность выделения и мечения молекул РНК (от последовательности)
- эффективность гибридизации
- точность и чувствительность измерения сигнала
Для систематических вариаций (считают одинаково воздействующими на сравниваемые образцы) используют следующие методы[16]:
- различия в нуклеотидном составе последовательностей могут приводит к различиям в представленности фрагментов в библиотеке анализируемого образца
- для генов большей длины картируется больше фрагментов
- при изготовлении библиотеки кДНК с поли-Т праймера представленность фрагментов возрастает от начала к концу гена
При этом простые подходы к нормализации учитывают лишь суммарное количество фрагментов сравниваемых образцов, а малое количество генов повысивших экспрессию может привести к ложному выявлению значительного количества генов снизивших экспрессию[16].
Также часто вместе или вместо значений количества картируемых фрагментов используют величины RPKM — Read Per Kilobase per Million mapped reads либо FPKM — Fragments Per Kilobase per Million mapped reads[16].
Методы[править | править код]
Все методы нормализации предполагают, что большая часть генов в сравниваемых образцах экспрессируется одинаково и доля генов снизивших экспрессию (downregulated) более или менее равна доле повысивших (upregulated). TMM (Trimmed Mean of M-values) и используемый в пакете DESeq[17].
Парное сравнение[править | править код]
Для поиска используется сравнение двух групп образцов и поиск генов, чьи уровни экспрессии значимо отличаются между двумя группами. Для каждого гена проверяют изменилась ли его экспрессия. Предполагают, что данные являются набором повторных измерений для каждого гена и , представляющих измеренный уровень экспрессии или его логарифм в исследуемом (treatment) и контрольном (control) образцах. Используемые методы можно разделить на непрерывные (t-тест) и дискретные (PPDE)[18][19].
При анализе данных, полученных с использованием микрочипов, полученные измерения трактуют как непрерывные величины (логнормальное распределение). При анализе данных RNA-Seq используют Пуассоновское распределение, обратное биномиальное и даже бета-биномиальное[20].
Фиксированный порог относительного изменения экспрессии[править | править код]
В ранних работах использовали подход при котором ген считался дифференциально экспрессируемым, если относительное изменение его экспрессии превысило некоторый порог (обычно 2)[21].
Простой t-тест[править | править код]
t-тест — хорошо известный критерий оценки равенства средних с учётом вариации. Рассчитывают нормализованное расстояние, используя выборочные средние и контрольного и исследуемого образцов соответственно и их дисперсии и , по формуле[22]
,
где и . Известно что распределение t близко к распределению Стьюдента с количеством степеней свободы f, где[22]
.
При превышении t некоторого порога, зависящего от выбранного уровня значимости, ген считают изменившим экспрессию[22].
Так как в t-тесте расстояние нормализуют выборочным стандартным отклонением, его применение предпочтительнее, чем использование фиксированного порога относительного изменения экспрессии[22].
Основная проблема применения t-теста заключена в малом количестве повторностей измерения и вследствие дороговизны или сложности эксперимента[22].
Регуляризованный t-тест[править | править код]
Данный метод используют для оценки вариабельности гена при помощи информации о других генах. Значения логарифма экспрессии генов моделируют как независимые нормальные распределения, параметризуемые соответствующими средними и дисперсиями[23].
,
где C — константа для нормализации распределения[23].
Для и принимают априорные вероятности — scaled inverse gamma и — распределено нормально[23].
Показано, что существует взаимоотношение между значением и вариацией экспрессии. При близких значениях экспрессии наблюдают близкие значения вариации экспрессии. Таким образом возможно приложение априорного знания в Байесовой статистике для получения лучших оценок вариации экспрессии отдельного гена, используя значения измеренного уровня экспрессии значительного числа других генов с близким уровнем экспрессии из того же эксперимента[23].
,
где
,
,
,
Для точечных оценок используют среднее апостериорной оценки (MP) либо моду (MAP — maximum a posteriori)[24].
В гибкой реализации, фоновую дисперсию экспрессии гена вычисляют, принимая во внимание гены, соседствующие с рассматриваемым, например 100 генов попадающие в симметричное окно по уровню экспрессии[24].
Хотя этот метод не исключает необходимости повторностей измерений, его использование позволяет значительно сократить число ложно-положительных находок даже при небольшом количестве повторов[24].
Оценка вероятности дифференциальной экспрессии[править | править код]
PPDE (Posterior Probability of Differential Expression), постариорная вероятность дифференциальной экспрессии[25].
По причине зашумлённости и вариабельности измеряемых данных ожидают получение ложно-положительных и ложно-отрицательных находок дифференциально экспрессирующихся генов[26].
Интуитивным способом оценки уровня ложно-положительных находок является сравнение измерений полученных с одного контрольного образца, при этом экспрессия генов не должна измениться[26].
Предложена также более формальная вычислительная реализация такого подхода: априорные знания основываются на наблюдении, что в случае отсутствия изменений экспрессии генов p-value по каждому гену должно быть распределено равномерно между 0 и 1 (доля генов ниже любого значения p равна p и доля выше равна 1-p). В случае наличия изменений распределение значений p-value для генов будет «стягиваться» больше к 0 чем к 1, то есть будет подмножество дифференциально экпрессирующихся генов с «значимыми» p-value. Это распределение моделируют взвешенной комбинацией равномерного и неравномерного распределений. Для каждого гена рассчитывают вероятность его ассоциации с неравномерным распределением — PPDE[27].
При моделировании используют смесь бета-распределений[27], где равномерное является частным случаем[27].
Обычно используют EM-алгоритм для определения весов в смеси[27].
Апостериорную вероятность дифференциальной экспрессии рассчитывают[27].
Часто в реализации предполагают, что значения p-value получены из распределения t-test как новые данные и строят вероятностную модель с ними[27].
Алгоритмы[править | править код]
Исходными данными методов/программ анализа дифференциально экспрессирующихся генов являются матрицы, содержащие данные о количестве фрагментов, картированных на ген/экзон для каждого образца в эксперименте RNA-Seq. В основном данные отсчётов используются прямо (baySeq [28] , EBSeq [29], ShrinkSeq [30], edgeR [31], DESeq [17], NBPSeq [32] и TSPM [33]), но существуют алгоритмы, преобразующие отсчёты и использующие алгоритмы, предназначенные для анализа данных, полученных гибридизационными микрочипами ( NOISeq [34] и SAMseq [35]).
Значительно ускорить обработку данных по РНК позволяют «лёгкие алгоритмы» Sailfish[36]
Модели[править | править код]
Параметрические[править | править код]
Признано, что для анализа дифференциальной экспрессии критично получение надёжной оценки параметра дисперсии для каждого гена, в этом направлении сосредоточено много усилий. Получение этой оценки осложнено малым размером выборки в большинстве экспериментов RNA-seq, что мотивирует разделение информации между генами для получения более точных оценок. Первым предположением было принять, что параметр дисперсии одинаков для всех генов, что позволяло оценивать его, используя все имеющиеся данные методом условного максимального правдоподобия. DESeq, edgeR, NBPSeq используют разделение данных генов для оценки дисперсии, различия заключаются в способе. В edgeR используют менее ограничивающий подход — дисперсию определяют для каждого гена, но индивидуальные оценки «стягивают» к общей дисперсии методом взвешенного правдоподобияe dgeR [31],[17],[32].
Большая часть параметрических моделей (baySeq, DESeq, edgeR и NBPSeq) использует модель обратного биномиального распределения для объяснения избытка дисперсии[31],[17],[32].
TSPM (Two-Stage Poisson Model) основана на модели Пуассона для отсчётов, расширенной с помощью подхода квази-правдоподобия для описания избытка дисперсии данных. Первым шагом каждый ген тестируют индивидуально на наличие избыточной дисперсии, чтобы решить какую из двух модель использовать для анализа дифференциальной экспрессии. Тестирование дифференциальной экспрессии основано на асимптотической статистике, которая предполагает, что общее количество фрагментов для каждого гена не слишком мало. Авторы рекомендуют отбрасывать гены, для которых общее число фрагментов менее 10. Также важно присутствие в данных генов без избыточной дисперсии[33]).
ShrinkSeq позволяет пользователю выбрать из набора распределений, включая обратное биномиальное и обратное биномиальное с избыточным числом нулевых значений[30].
DESeq, edgeR, NBPSeq используют классический подход проверки гипотезы[31],[32]. baySeq, EBSeq, ShrinkSeq используют байесову статистику[28][29][30].
В DESeq и NBPSeq получают оценки дисперсии, моделируя наблюдаемую зависимость между средним и дисперсией локальной или параметрической регрессией. В NBPSeq используют полученные значения дисперсии, в DESeq используют консервативный подход — выбирают наибольшее значение дисперсии (из оценки с разделением информации о других генах и оценки дисперсии для индивидуального гена). В edgeR, DESeq и NBPSeq значимость дифференциальной экспрессии тестируют разновидностью точного теста (для сравнения двух групп) либо обобщённой линейной моделью[31][17][32].
В baySeq пользователь задаёт коллекцию моделей, разбивающих образцы на группы. В группе предполагают одинаковые параметры основного распределения. Затем оценивают апостериорную вероятность каждой модели для каждого из генов. Информация из всего набора генов используется для формирования эмпирического априорного распределения для параметров обратного биномиального распределения[28].
EBSeq использует подобный подход, но предполагает параметрическую форму априорного распределения параметров, с гиперпараметрами, разделяемыми между всеми генами и оцениваемыми по данным[29].
Непараметрические[править | править код]
В NOISeq и SAMSeq — непараметрические методы, не предполагают какого-либо распределения для данных[37],[38] .
SAMSeq основан на статистике Вилкоксона, усреднённой по нескольким оценкам данных с использованием пермутаций, для оценки FDR (false discovery rate). Эти оценки используют для определения q-value для каждого гена[38].
В NOISeq определяют распределение крастности изменения и различия абсолютных значений экспрессии между образцами при различных условиях и сравнивают это распределение с полученным при сравнении образцов при одних условиях (называют «распределением шума»). Кратко, для каждого гена рассчитывают статистику, определяемую как доля точек из распределения шума, соответствующих более низкой кротности изменения и разности абсолютных значений экспрессии, чем полученные для интересующего гена в исходных данных[37].
Множественное сравнение[править | править код]
При сравнение экспрессии генов в нескольких экспериментах либо проводят множественные попарные сравнения, либо используют модели, в которых сравниваются группы экспериментов. В случае, когда рассматривается Κ воздействий (например, лечение), Τ0…Τκ-1, на экспрессию генов, можно использовать несколько принципиально отличающихся планов сравнения[39][40].
- Непрямое сравнение — попарные сравнения каждого эксперимента (Τ0…Τκ-1) с контролем;
- Прямое сравнение — попарное сравнение серий экспериментов, например T0 c T1, T1 с T2 и т. д.
- Сравнение всех возможных пар[41],[42]
При сравнение большого количества экспериментов необходимо использовать поправку на множественное сравнение (FDR, FWER, adjusted p-value или другие)[43], чтобы исключить возможность случайного получить значимое различие в экспрессии генов. Использование только попарных сравнений при анализе большого количества групп экспериментов (факторов) не оптимально, поскольку требует значительных временных затрат. В подобных случаях более рационально использовать модели, учитывающие воздействия нескольких факторов[39][40].
- При сравнении эффектов действия одного фактора возможно использовать линейную модель (linear model). В данной модели предполагается нормальное распределение экспрессии генов, используется, как правило, для анализа микрочиповых данных. Для каждого гена создаётся подходящая линейная модель и через неё рассчитывается изменение уровня экспрессии гена (fold change, log-fold change и другие статистики), а также стандартная ошибка. Полученные данные отображаются на вулкан диаграмме (volcano plot) Значимость изменения уровня экспрессии генов определяется с помощью дисперсионного анализа (ANOVA). Далее возможно определить работа каких генов изменяется под действием изучаемого фактора. При анализе нескольких групп используются реплики (повторы) экспериментов для определения уровней внутригрупповой дисперсии, что позволяет учитывать технические факторы. Такая модель используется, например, в пакете программ limma Bioconductor.
- Обобщённая линейная модель (Generalized Linear Model, GLM), является усложнением линейной модели, её можно использовать для различных распределений данных (нормальное, биномиальное, экспоненциальное, Пуассона, гамма…). В качестве факторов можно рассматривать как непрерывные величины, так и дискретные.[44] Например, с помощью данной модели возможно анализировать данные RNA-Seq. Значимость дифференциальной экспрессии определяется с помощью функции правдоподобия. Подобный анализ можно проводить в пакетах программ таких как edgeR, или DESeq.
- Однофакторная дисперсионная модель (one-way ANOVA test) позволяет анализировать несколько независимых экспериментов (более трёх), при этом возможно выявить дифференциально экспрессирующиеся гены между любой парой выборок. Этот анализ удобен, если заранее не известно между какими выборками/экспериментами будет отличие, а также тем, что его результат не связан со способом определения групп. Фактически, данный анализ осуществляется через попарное сравнение уровней экспрессии всех генов и выявляет все пары между которыми разница ненулевая[40].
- Многомерная обобщённая линейная модель (multivariate general linear model) позволяет анализировать несколько зависимых групп экспериментов (в отличие от описанных выше моделей). Например, учитывать взаимосвязь экспрессии генов в двух разных тканях мозга[39].
Дизайн мультифакторных сравнений[править | править код]
Эксперименты, в которых рассматривается воздействие нескольких факторов, используются практически те же математические подходы (регрессионный анализ, байесовская статистика), что и при однофакторном анализе, но более сложный дизайн групповых сравнений. Вот некоторые из них[45].
- Вложенная модель (иерархическая)- подход, пример мультифакторной модели. В подобной модели некоторые факторы можно рассматривать иерархически. Например, учитывать несколько категорий (состояние, степень воздействия, пол, и т. п.), каждый объект можно классифицировать по данным признакам и далее проводить сравнение между интересующими группами.
- Временные ряды (Time series) — подход, при которой в течение эксперимента измеряют уровень экспрессии через определённые промежутки времени, рассматривают не только непрерывно распределённые, но и дискретные параметры. Например, с помощью подобной модели можно изучать динамику изменения работы генов в ответ на какие-либо условия.
- Аддитивная модель — подход, при котором изучается один и тот же объект (особь, линия) до и после воздействия, а далее сравниваются для каждого организма по отдельности и далее сопоставляется с группой организмов. Такая модель является частым случаем блокирования (Blocking), идеи о сравнении максимально схожих (по нескольким факторам) образцов[45].
Примечания[править | править код]
- ↑ Wang Z., Gerstein M., Snyder M. RNA-Seq: a revolutionary tool for transcriptomics (англ.) // Nat Rev Genet : journal. — 2009. — No. 1. — P. 57—63. — PMID 19015660.
- ↑ 1 2 A Mortazavi, BA Williams, K McCue, L Schaeffer, and B Wold. Mapping and quantifying mammalian transcriptomes by RNA-Seq (англ.) // Nature Methods : journal. — 2008. — No. 5. — P. 621—628. — PMID 18516045.
- ↑ 1 2 Pachter. MODELS FOR TRANSCRIPT QUANTIFICATION FROM RNA-SEQ (неопр.). — 2011.
- ↑ Trapnell C., Pachter L., Salzberg S. L. TopHat: discovering splice junctions with RNA-Seq (неопр.) // Bioinformatics. — 2009. — № 9. — С. 1105—1111. — PMID 19289445.
- ↑ 1 2 C Trapnell, BA Williams, G Pertea, A Mortazavi, G Kwan, MJ van Baren, SL Salzberg, BJ Wold,and L Pachter. Transcript assembly and quantification by RNA-Seq reveals unannotated transcripts and isoform switching during cell differentiation (англ.) // Nature Biotechnology : journal. — Nature Publishing Group, 2010. — No. 3. — P. 511—515. — PMID 20436464.
- ↑ Menschaert G., Fenyö D. Proteogenomics from a bioinformatics angle: A growing field (англ.) // Mass Spectrom Rev[англ.] : journal. — 2011. — P. 584—599.
- ↑ Trapnell C., Roberts A., Goff L., Pertea G., Kim D., Kelley D. R., Pimentel H., Salzberg S. L., Rinn J. L., Pachter L. Differential gene and transcript expression analysis of RNA-seq experiments with TopHat and Cufflinks (англ.) // Nat Protoc[англ.] : journal. — 2012. — No. 9. — P. 562—578. — PMID 22383036.
- ↑ 1 2 Chandramohan R., Wu P. Y., Phan J. H., Wang M. D. Benchmarking RNA-Seq quantification tools (неопр.) // Conf Proc IEEE Eng Med Biol Soc. — 2013. — С. 647—650. — PMID .6609583.
- ↑ Roberts A., Trapnell C., Donaghey J., Rinn J. L., Pachter L. Improving RNA-Seq expression estimates by correcting for fragment bias (англ.) // BioMed Central[англ.] : journal. — 2011. — Vol. 12, no. 3. — P. 280—287. — PMID 21498551.
- ↑ Refour P., Gissot M., Siau A., Mazier D., Vaquero C. Progress towards the use of DNA microarray technology for the study of wild Plasmodium strains (англ.) // Med Trop : journal. — 2004. — Vol. 64, no. 4. — P. 387—393. — PMID 21498551.
- ↑ 1 2 3 Ravi Kothapalli, Sean J Yoder, Shrikant Mane, and Thomas P Loughran, Jr. Microarray results: how accurate are they? (англ.) // BMC Bioinformatics[англ.] : journal. — 2002. — PMID 12194703.
- ↑ 1 2 3 4 Ares M Jr. Microarray slide hybridization using fluorescently labeled cDNA (англ.) // Cold Spring Harb Protoc : journal. — 2014. — No. 2. — P. 124—129. — PMID 24371320.
- ↑ 1 2 Maria Jackson, Leah Marks, Gerhard H.W. May, and Joanna B. Wilson. The genetic basis of disease (неопр.) // Essays Biochem. — 2018. — Т. 62, № 5. — С. 643—723. — PMID 30509934.
- ↑ 1 2 Yan Sun, Suli Zhang, Mingming Yue, Yang Li, Jing Bi, and Huirong Liu. Angiotensin II inhibits apoptosis of mouse aortic smooth muscle cells through regulating the circNRG-1/miR-193b-5p/NRG-1 axis (англ.) // Cell Death Dis : journal. — 2019. — Vol. 10, no. 5. — P. 362. — PMID 31043588.
- ↑ 1 2 3 4 5 6 7 G. Wesley Hatfield, She-pin Hung and Pierre Baldi. Differential analysis of DNA microarray gene expression data (англ.) // Molecular Microbiology : journal. — 2003. — Vol. 47, no. 4. — P. 871—877. — PMID 12581345.
- ↑ 1 2 3 4 Charity W. Law, Monther Alhamdoosh, Shian Su, Xueyi Dong, Luyi Tian, Gordon K. Smyth, and Matthew E. Ritchie,. RNA-seq analysis is easy as 1-2-3 with limma, Glimma and edgeR (англ.) // Version 3. F1000Res : journal. — 2018. — Vol. 5. — PMID 27441086.
- ↑ 1 2 3 4 5 Simon Anders, Wolfgang Huber. Differential expression analysis for sequence count data (англ.) // BioMed Central[англ.] : journal. — 2010. — Vol. 11. — PMID 20979621.
- ↑ Gregory R. Smith and Marc R. Birtwistle. A Mechanistic Beta-Binomial Probability Model for mRNA Sequencing Data (англ.) // PLoS One : journal. — 2016. — Vol. 11, no. 6. — PMID 27326762.
- ↑ Steven M. Sanders, and Paulyn Cartwright. Interspecific Differential Expression Analysis of RNA-Seq Data Yields Insight into Life Cycle Variation in Hydractiniid Hydrozoans (англ.) // Genome Biol Evol[англ.] : journal. — 2015. — Vol. 7, no. 8. — PMID 26251524.
- ↑ Gregory R. Smith and Marc R. Birtwistle. A Mechanistic Beta-Binomial Probability Model for mRNA Sequencing Data (англ.) // BIOINFORMATICS : journal. — 2016. — Vol. 11, no. 6. — PMID 27326762.
- ↑ A I Hartstein, V H Morthland, S Eng, G L Archer, F D Schoenknecht, and A L Rashad. Restriction enzyme analysis of plasmid DNA and bacteriophage typing of paired Staphylococcus aureus blood culture isolates (англ.) // J Clin Microbio : journal. — 1989. — Vol. 27, no. 8. — P. 1874—1879. — PMID 2527867.
- ↑ 1 2 3 4 5 Bland, Martin. An Introduction to Medical Statistics (неопр.). — Oxford University Press, 1995. — С. 168. — ISBN 978-0-19-262428-4.
- ↑ 1 2 3 4 Johnson, N.L., Kotz, S., Balakrishnan, N. Continuous Univariate Distributions, Volume 2, 2nd Edition. — 1995. — ISBN 0-471-58494-0.
- ↑ 1 2 3 Pierre Baldi and Anthony D. Long. A Bayesian framework for the analysis of microarray expression data: regularized t-test and statistical inferences of gene changes (англ.) // BIOINFORMATICS : journal. — 2001. — Vol. 17, no. 6. — P. 509—519. — PMID 11395427.
- ↑ Mayer Aladjem, Itamar Israeli-Ran ; Maria Bortman. Sequential Independent Component Analysis Density Estimation (англ.) // IEEE Transactions on Neural Networks and Learning Systems[англ.] : journal. — 2018. — Vol. 29, no. 10. — P. 5084—5097. — PMID 29994425.
- ↑ 1 2 Arfin SM et all. Global gene expression profiling in Escherichia coli K12. The effects of integration host factor (англ.) // J Biol Chem : journal. — 2000. — Vol. 275, no. 38. — P. 29672—29684. — PMID 10871608.
- ↑ 1 2 3 4 5 6 David B. Allison. A mixture model approach for the analysis of microarray gene expression data (англ.) // Computational Statistics & Data Analysis[англ.] : journal. — 2002. — Vol. 39, no. 1. — P. 1—20. — doi:10.1016/S0167-9473(01)00046-9.
- ↑ 1 2 3 Thomas J Hardcastle and Krystyna A Kelly. baySeq: Empirical Bayesian methods for identifying differential expression in sequence count data (англ.) // BMC Bioinformatics[англ.] : journal. — 2010. — Vol. 11. — doi:10.1186/1471-2105-11-422.
- ↑ 1 2 3 Ning Leng, John A. Dawson, James A. Thomson, Victor Ruotti, Anna I. Rissman, Bart M.G. Smits, Jill D. Haag, Michael N. Gould, Ron M. Stewart and Christina Kendziorski. EBSeq: an empirical bayes hierarchical model for inference in RNA-seq experiments (англ.) // University of Wisconsin: Tech. Rep. 226, Department of Biostatistics and Medical Informatics : journal. — 2012. Архивировано 20 февраля 2014 года.
- ↑ 1 2 3 Mark A. Van De Wiel, Gwenaël G.R. Leday, Luba Pardo, Håvard Rue, Aad W. Van Der Vaart, Wessel N. Van Wieringen. Bayesian analysis of RNA sequencing data by estimating multiple shrinkage priors (англ.) // Biostatistics : journal. — 2012. — Vol. 14, no. 1. — P. 113—128. — PMID 22988280.
- ↑ 1 2 3 4 5 Mark D. Robinson, Davis J. McCarthy and Gordon K. Smyth. EdgeR: a bioconductor package for differential expression analysis of digital gene expression data (англ.) // Bioinformatics : journal. — 2010. — Vol. 26, no. 1. — P. 139—140. — PMID 19910308.
- ↑ 1 2 3 4 5 Yanming Di, Daniel W. Schafer, Jason S. Cumbie and Jeff H. Chang. The NBP negative binomial model for assessing differential gene expression from RNA-seq (англ.) // Statistical Applications in Genetics and Molecular Biology[англ.] : journal. — 2011. — Vol. 10.
- ↑ 1 2 Paul L. Auer and Rebecca W. Doerge. A two-stage poisson model for testing RNA-seq data (англ.) // Statistical Applications in Genetics and Molecular Biology[англ.] : journal. — 2011. — Vol. 10. Архивировано 12 июня 2011 года.
- ↑ Sonia Tarazona, Fernando García-Alcalde, Joaquin Dopazo, Alberto Ferrer and Ana Conesa. Differential expression in RNA-seq: a matter of depth (англ.) // Genome Research[англ.] : journal. — 2011. — Vol. 21. — P. 2213—2223. — doi:10.1101/gr.124321.111.
- ↑ Li J and Tibshirani R. Finding consistent patterns: a nonparametric approach for identifying differential expression in RNA-seq data (англ.) // Statistical Methods in Medical REsearch : journal. — 2011. — PMID 22127579.
- ↑ Rob Patro, Stephen M Mount, Carl Kingsford.(2014) Sailfish enables alignment-free isoform quantification from RNA-seq reads using lightweight algorithms. Nature Biotechnology, doi:10.1038/nbt.2862
- ↑ 1 2 Tarazona S., Furió-Tarí P., Turrà D., Di Pietro A., Nueda M. J., Ferrer A., et al. Data quality aware analysis of differential expression in RNA-seq with NOISeq R/Bioc package (англ.) // Nucleic acids researchy : journal. — 2015. — doi:10.1093/nar/gkv711.
- ↑ 1 2 Li J., Tibshirani R. Finding consistent patterns: a nonparametric approach for identifying differential expression in RNA-Seq data (англ.) // Statistical methods in medical research : journal. — 2013. — P. 519—536. — doi:10.1177/0962280211428386.
- ↑ 1 2 3 Yu Okamura, Natsumi Tsuzuki, Shiori Kuroda, Ai Sato, Yuji Sawada, Masami Yokota Hirai, and Masashi Murakami. Interspecific Differences in the Larval Performance of Pieris Butterflies (Lepidoptera: Pieridae) Are Associated with Differences in the Glucosinolate Profiles of Host Plants (англ.) : journal. — 2019. — P. 2. — PMID 31039584.
- ↑ 1 2 3 Mollah MM1, Jamal R1, Mokhtar NM2, Harun R1, Mollah MN3. A Hybrid One-Way ANOVA Approach for the Robust and Efficient Estimation of Differential Gene Expression with Multiple Patterns (англ.) // PLoS One : journal. — 2015. — PMID 26413858.
- ↑ Yang Y.H. , Speed T.P. (2003). "«Design and Analysis of Comparative Microarray Experiments». Statistical Analysis of Gene Expression Microarray Data". Chapman & Hall., New York,: 35—92. ISBN 1-58488-327-8.
{{cite journal}}: Википедия:Обслуживание CS1 (лишняя пунктуация) (ссылка) - ↑ Smyth, G. K. Linear models and empirical Bayes methods for assessing differential expression in microarray experiments (англ.) // Statistical Applications in Genetics and Molecular Biology[англ.] : journal. — 2004. — Vol. 3. — doi:10.2202/1544-6115.1027.
- ↑ Sandrine Dudoit, Juliet Popper Shaffer and Jennifer C. Boldrick. Multiple Hypothesis Testing in Microarray Experiments (англ.) // Statistical Science[англ.] : journal. — 2003. — Vol. 18. — P. 71—103. — doi:10.0000/projecteuclid.org/euclid.ss/1056397487.
- ↑ Nelder J., Wedderburn R. Generalized Linear Models (неопр.) // [Journal of the Royal Statistical Society]. Series A (General). — Blackwell Publishing, 1972. — Т. 135, № 3. — С. 370—384. — doi:10.2307/2344614. — .
- ↑ 1 2 Robinson M. D., McCarthy D. J., Smyth GK. edgeR: a Bioconductor package for differential expression analysis of digital gene expression data (англ.) // Bioinformatics : journal. — 2010. — Vol. 26. — P. 139—140. — doi:10.1093/bioinformatics/btp616.
Ссылки[править | править код]
- Charlotte Soneson and Mauro Delorenzi — A comparison of methods for differential expression analysis of RNA-seq data — BMC Bioinformatics, 2013, 14:91
Для улучшения этой статьи желательно:
|













![{\textstyle f={\frac {\left[\left(s_{c}^{2}/n_{c}\right)+\left(s_{t}^{2}/n_{t}\right)\right]^{2}}{{\frac {\left(s_{c}^{2}/n_{c}\right)^{2}}{n_{c}-1}}+{\frac {\left(s_{t}^{2}/n_{t}\right)^{2}}{n_{t}-1}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bba4358fa3cf8df67824d5a6975b70c690cf35ad)















