Бета-распределение

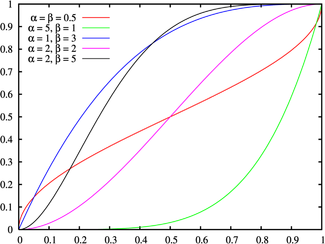Бета-распределение
Плотность вероятности
Функция распределения
Обозначение	${\text{Beta}}(\alpha ,\beta )$
Параметры	$\alpha >0$ $\beta >0$
Носитель	$x\in [0,1]$
Плотность вероятности	${\frac {x^{\alpha -1}(1-x)^{\beta -1}}{\mathrm {B} (\alpha ,\beta )}}$
Функция распределения	$I_{x}(\alpha ,\beta )$
Математическое ожидание	${\frac {\alpha }{\alpha +\beta }}$
Мода	${\frac {\alpha -1}{\alpha +\beta -2}}$ для $\alpha >1,\beta >1$
Дисперсия	${\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}$
Коэффициент асимметрии	${\frac {2\,(\beta -\alpha ){\sqrt {\alpha +\beta +1}}}{(\alpha +\beta +2){\sqrt {\alpha \beta }}}}$
Коэффициент эксцесса	$6\,{\frac {\alpha ^{3}-\alpha ^{2}(2\beta -1)+\beta ^{2}(\beta +1)-2\alpha \beta (\beta +2)}{\alpha \beta (\alpha +\beta +2)(\alpha +\beta +3)}}$
Производящая функция моментов	$1+\sum _{k=1}^{\infty }\left(\prod _{r=0}^{k-1}{\frac {\alpha +r}{\alpha +\beta +r}}\right){\frac {t^{k}}{k!}}$
Характеристическая функция	${}_{1}F_{1}(\alpha ;\alpha +\beta ;i\,t)$

Бе́та-распределе́ние в теории вероятностей и статистике — двухпараметрическое семейство абсолютно непрерывных распределений. Используется для описания случайных величин, значения которых ограничены конечным интервалом.

Определение

Пусть распределение случайной величины $X$ задаётся плотностью вероятности $f_{X}$, имеющей вид:

$f_{X}(x)={\frac {1}{\mathrm {B} (\alpha ,\beta )}}\,x^{\alpha -1}(1-x)^{\beta -1}$,

где

• $\alpha ,\beta >0$ произвольные фиксированные параметры, и
• $\mathrm {B} (\alpha ,\beta )=\int \limits _{0}^{1}x^{\alpha -1}(1-x)^{\beta -1}\,dx$ — бета-функция.

Тогда случайная величина $X$ имеет бета-распределение. Пишут: $X\!\sim \mathrm {B} (\alpha ,\beta )$.

Форма графика

Форма графика плотности вероятности бета-распределения зависит от выбора параметров $\alpha$ и $\beta$.

• $\alpha <1,\ \beta <1$ — график выпуклый и уходит в бесконечность на границах (красная кривая);
• $\alpha <1,\ \beta \geq 1$ или $\alpha =1,\ \beta >1$ — график строго убывающий (синяя кривая)
  • $\alpha =1,\ \beta >2$ — график строго выпуклый;
  • $\alpha =1,\ \beta =2$ — график является прямой линией;
  • $\alpha =1,\ 1<\beta <2$ — график строго вогнутый;
• $\alpha =1,\ \beta =1$ график совпадает с графиком плотности стандартного непрерывного равномерного распределения;
• $\alpha =1,\ \beta <1$ или $\alpha >1,\ \beta \leq 1$ — график строго возрастающий (зелёная кривая);
  • $\alpha >2,\ \beta =1$ — график строго выпуклый;
  • $\alpha =2,\ \beta =1$ — график является прямой линией;
  • $1<\alpha <2,\ \beta =1$ — график строго вогнутый;
• $\alpha >1,\ \beta >1$ — график унимодальный (пурпурная и чёрная кривые)

В случае, когда $\alpha =\beta$, плотность вероятности симметрична относительно $1/2$ (красная и пурпурная кривые), то есть

$f_{X}(1/2-x)=f_{X}(1/2+x),\;x\in [0,1/2]$.

Моменты

Математическое ожидание и дисперсия случайной величины $X$, имеющей бета-распределение, имеют вид:

$\mathbb {E} [X]={\frac {\alpha }{\alpha +\beta }}$,

$\mathrm {D} [X]={\frac {\alpha \beta }{(\alpha +\beta )^{2}(\alpha +\beta +1)}}$.

Моменты старших порядков случайной величины $X$, имеющей бета-распределение, имеют вид:

$\mathbb {E} [X^{k}]={\frac {\alpha ^{(k)}}{(\alpha +\beta )^{(k)}}}=\prod _{r=0}^{k-1}{\frac {\alpha +r}{\alpha +\beta +r}}$

где (x)^(k) - возрастающий факториал.

Связь с другими распределениями

• Бета-распределение является распределением Пирсона типа I.
• Стандартное непрерывное равномерное распределение является частным случаем бета-распределения:

  $\mathrm {U} [0,1]\equiv \mathrm {B} (1,1)$.

• Бета-распределение широко используется в байесовской статистике, так как оно является сопряжённым априорным распределением для распределения Бернулли, биномиального и геометрического распределений.
• Если $X,Y$ — независимые гамма-распределённые случайные величины, причём $X\sim \mathrm {\Gamma } (\alpha ,1)$, а $Y\sim \mathrm {\Gamma } (\beta ,1)$, то

  ${\frac {X}{X+Y}}\sim \mathrm {B} (\alpha ,\beta )$ .

Литература

• Королюк В.С., Портенко Н.И.,Скороход А.В., Турбин А.Ф. Справочник по теории вероятностей и математической статистике. — М.: Наука, 1985. — 640 с.