Криволинейная система координат
Криволине́йная систе́ма координа́т, или криволине́йные координа́ты, — система координат в евклидовом (аффинном) пространстве, или в области, содержащейся в нём. Криволинейные координаты не противопоставляются прямолинейным, последние являются частным случаем первых. Применяются обычно на плоскости (n=2) и в пространстве (n=3); число координат равно размерности пространства n. Наиболее известным примером криволинейной системы координат являются полярные координаты на плоскости.
Локальные свойства криволинейных координат[править | править код]
При рассмотрении криволинейных координат в данном разделе мы будем полагать, что рассматриваем трёхмерное пространство (n=3), снабжённое декартовыми координатами x, y, z. Случай других размерностей отличается лишь количеством координат.
В случае евклидова пространства метрический тензор, именуемый также квадратом дифференциала дуги, будет в этих координатах иметь вид, соответствующий единичной матрице:
Общий случай[править | править код]

Пусть , , — некие криволинейные координаты, которые мы будем считать заданными гладкими функциями от x, y, z. Для того, чтобы три функции , , служили координатами в некоторой области пространства, необходимо существование обратного отображения:
где — функции, определённые в некоторой области наборов координат.
Этот раздел не завершён. |
Локальный базис и тензорный анализ[править | править код]
В тензорном исчислении можно ввести векторы локального базиса: , где — орты декартовой системы координат, — матрица Якоби, координаты в декартовой системе, — вводимые криволинейные координаты.
Нетрудно видеть, что криволинейные координаты, вообще говоря, меняются от точки к точке.
Укажем формулы для связи криволинейных и декартовых координат:
где , где Е — единичная матрица.
Произведение двух векторов локального базиса образует метрическую матрицу:
, где контравариантный, ковариантный и смешанный символ Кронекера
Таким образом любое поле тензора ранга n можно разложить по локальному полиадному базису:
Например, в случае поле тензора первого ранга (вектора) :
Ортогональные криволинейные координаты[править | править код]
В евклидовом пространстве особое значение имеет использование ортогональных криволинейных координат, поскольку формулы, имеющие отношение к длине и углам, выглядят в ортогональных координатах проще, нежели в общем случае. Что связано с тем, что метрическая матрица в системах с ортонормированным базисом будет диагональной, что существенно упростит расчёты.
В качестве примера таких систем можно привести сферическую систему в
Коэффициенты Ламе[править | править код]
Выпишем дифференциал дуги в криволинейных координатах в виде (используется правило суммирования Эйнштейна):
Принимая во внимание ортогональность систем координат ( при ) это выражение можно переписать в виде
где
Положительные величины , зависящие от точки пространства, именуются коэффициентами Ламе или масштабными коэффициентами. Коэффициенты Ламе показывают, сколько единиц длины содержится в единице координат данной точки и используются для преобразования векторов при переходе от одной системы координат к другой.
Тензор римановой метрики, записанный в координатах , представляет собой диагональную матрицу, на диагонали которой стоя́т квадраты коэффициентов Ламе:
для i≠j |
, то есть |
Примеры[править | править код]
Полярные координаты (n=2)[править | править код]
Полярные координаты на плоскости включают расстояние r до полюса (начала координат) и направление (угол) φ.
Связь полярных координат с декартовыми:
Коэффициенты Ламе:
Дифференциал дуги:
В начале координат функция φ не определена. Если координату φ считать не числом, а углом (точкой на единичной окружности), то полярные координаты образуют систему координат в области, полученной изо всей плоскости изъятием точки начала координат. Если всё-таки считать φ числом, то в обозначенной области оно будет многозначно, и построение строго в математическом смысле системы координат возможно лишь в односвязной области, не включающей начало координат, например, на плоскости без луча.
Цилиндрические координаты (n=3)[править | править код]
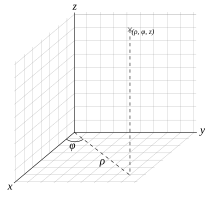
Цилиндрические координаты являются тривиальным обобщением полярных на случай трёхмерного пространства путём добавления третьей координаты z. Связь цилиндрических координат с декартовыми:
Коэффициенты Ламе:
Дифференциал дуги:
Сферические координаты (n=3)[править | править код]

Сферические координаты связаны с координатами широты и долготы на единичной сфере. Связь сферических координат с декартовыми:
Коэффициенты Ламе:
Дифференциал дуги:
Сферические координаты, как и цилиндрические, не работают на оси z {x=0, y=0}, поскольку координата φ там не определена.
Различные экзотические координаты на плоскости (n=2) и их обобщения[править | править код]
Ортогональные:
- Эллиптические координаты — расширяются до 3 измерений
- Параболические координаты — расширяются до 3 измерений
- Биполярные координаты — расширяются до 3 измерений
- …
Прочие:
…
Этот раздел не завершён. |
Криволинейные координаты с точки зрения дифференциальной геометрии[править | править код]
Криволинейные координаты, определённые в различных областях евклидова (аффинного) пространства, можно рассматривать как применение к пространству понятия гладкого многообразия. А именно, как построение атласа карт.
Этот раздел не завершён. |
Литература[править | править код]
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1974. — 832 с.
Для улучшения этой статьи желательно:
|
В другом языковом разделе есть более полная статья Curvilinear coordinates (англ.). |










































