Операция «Snub»
Эту страницу предлагается переименовать в «Отсечение вершин». |
 Плосконосый куб или плосконосый кубооктаэдр |
 Плосконосый додекаэдр или плосконосый икосододекаэдр |


Операция snub или отсечение вершин — это операция, применяемая к многогранникам. Термин появился из названий, данных Кеплером двум архимедовым телам — плосконосый куб (cubus simus) и плосконосый додекаэдр (dodecaedron simum)[1]. В общем случае плосконосые формы имеют хиральную симметрию двух видов, с ориентацией по часовой стрелке и против часовой стрелки. Согласно названиям Кеплера, отсечение вершин можно рассматривать как растяжение правильного многогранника, когда исходные грани отодвигаются от центра и поворачиваются относительно центров, вместо исходных вершин добавляются многоугольники с центрами в этих вершинах, а пары треугольников заполняют пространство между исходными рёбрами.
Терминологию обобщил Коксетер со слегка другим определением для более широкого множества однородных многогранников.
Операция «snub» Конвея
[править | править код]Джон Конвей исследовал обобщённые операции над многогранниками, определяя то, что называется теперь нотацией Конвея для многогранников, которая может быть применена к многогранникам и мозаикам. Конвей назвал операцию Коксетера semi-snub (полу-snub)[2].
В этой нотации snub определяется как композиция двойственного и gyro операторов, , и это эквивалентно последовательности операторов альтернирования[англ.], усечения и ambo. Нотация Конвея избегает операции альтернирования, поскольку та применима только к многогранниками с гранями, имеющими чётное число сторон.
| Многогранники | Евклидовы мозаики | Гиперболические мозаики | ||||
|---|---|---|---|---|---|---|
| Нотация Конвея |
sT | sC = sO | sI = sD | sQ | sH = sΔ | sΔ7 |
| Плосконосый многогранник |
Тетраэдр | Куб или Октаэдр |
Икосаэдр или Додекаэдр |
Квадратная мозаика | Шестиугольная мозаика или Треугольная мозаика |
Семиугольная мозаика или Треугольная мозаика порядка 7[англ.] |
| Рисунок | 
|

|

|

|

|

|
В 4-мерных пространствах Конвей считает, что плосконосый 24-ячейник[англ.] должен называться полуплосконосым 24-ячейником, поскольку он не представляет альтернированный всеусечённый 24-ячейник[англ.], как его аналог в 3-мерном пространстве. Вместо этого он является альтернированным усечённым 24-ячейником[англ.][3].
Операции «snub» Коксетера, правильная и квазиправильная
[править | править код]| Исходное тело | Полноусечённый многогранник r |
Усечённый многогранник t |
Альтернированный многогранник[англ.] h |
|---|---|---|---|
| Cube |
Кубооктаэдр Полноусечённый куб |
Усечённый кубооктаэдр Скошено-усечённый куб |
Плосконосый кубооктаэдр Плосконосый полноусечённый куб |
| C | CO rC |
tCO trC или trO |
htCO = sCO htrC = srC |
| {4,3} | или r{4,3} | или tr{4,3} | htr{4,3} = sr{4,3} |

|

|

|
Терминология «snub» (отсечения вершин) Коксетера несколько отличается и означает альтернированное[англ.] усечение, по которому плосконосый куб получается операцией snub (отсечение вершин) из кубооктаэдра, а плосконосый додекаэдр — из икосододекаэдра. Это определение используется в названиях двух тел Джонсона — плосконосый двуклиноид и плосконосая квадратная антипризма, а также в названиях многогранников более высокой размерности, таких как 4-мерный плосконосый 24-ячейник[англ.], ![]()
![]()
![]()
![]()
![]()
![]()
![]() или s{3,4,3}.
или s{3,4,3}.
Правильный многогранник (или мозаика) с символом Шлефли, и диаграммой Коксетера ![]()
![]()
![]()
![]()
![]() имеет усечение, определённое как с диаграммой
имеет усечение, определённое как с диаграммой ![]()
![]()
![]()
![]()
![]() , и плосконосую форму, определённую как альтернированное[англ.] усечение с диаграммой Коксетера
, и плосконосую форму, определённую как альтернированное[англ.] усечение с диаграммой Коксетера ![]()
![]()
![]()
![]()
![]() . Это построение требует, чтобы q было чётным.
. Это построение требует, чтобы q было чётным.
Квазиправильный многогранник или r{p,q}, с диаграммой Коксетера ![]()
![]()
![]() или
или ![]()
![]()
![]()
![]()
![]() имеет квазиправильное усечение, определённое как или tr{p,q} (с диаграммой Коксетера
имеет квазиправильное усечение, определённое как или tr{p,q} (с диаграммой Коксетера ![]()
![]()
![]() или
или ![]()
![]()
![]()
![]()
![]() ) и квазиправильную плосконосую форму, определённую как альтернированное[англ.] усечение полного усечения или htr{p,q} = sr{p,q} (с диаграммой Коксетера
) и квазиправильную плосконосую форму, определённую как альтернированное[англ.] усечение полного усечения или htr{p,q} = sr{p,q} (с диаграммой Коксетера ![]()
![]()
![]() или
или ![]()
![]()
![]()
![]()
![]() ).
).
Например, плосконосый куб Кеплера получается из квазирегулярного кубооктаэдра с вертикальным символом Шлефли (и диаграммой Коксетера ![]()
![]()
![]() ) и более точно называется плосконосый кубооктаэдр, который выражается символом Шлефли (с диаграммой Коксетера
) и более точно называется плосконосый кубооктаэдр, который выражается символом Шлефли (с диаграммой Коксетера ![]()
![]()
![]() ). Плосконосый кубооктаэдр является альтернацией усечённого кубооктаэдра (
). Плосконосый кубооктаэдр является альтернацией усечённого кубооктаэдра (![]()
![]()
![]() ).
).
Правильные многогранники с чётным порядком вершин также могут быть приведены к плосконосой форме как альтернированное усечение, подобно как плосконосый октаэдр (![]()
![]()
![]()
![]()
![]() ) (и плосконосый тетратетаэдр ,
) (и плосконосый тетратетаэдр , ![]()
![]()
![]() ) представляет псевдоикосаэдр, правильный икосаэдр с пиритоэдральной симметрией. Плосконосый октаэдр является альтернированной формой усечённого октаэдра, (
) представляет псевдоикосаэдр, правильный икосаэдр с пиритоэдральной симметрией. Плосконосый октаэдр является альтернированной формой усечённого октаэдра, (![]()
![]()
![]()
![]()
![]() ), или в форме тетраэдральной симметрии: и
), или в форме тетраэдральной симметрии: и ![]()
![]()
![]() .
.
| Усечённый t |
Альтернированный h | |
|---|---|---|
| Октаэдр O |
Усечённый октаэдр tO |
Плосконосый октаэдр htO или sO |
| {3,4} | t{3,4} | ht{3,4} = s{3,4} |

|

|
Операция отсечения вершин (носов) Коксетера позволяет также определить n-антипризму как или на основе n-призм или , а является правильным осоэдром, вырожденным многогранником, который является допустимой мозаикой на сфере с двуугольными или луноподобными гранями.
| Рисунок | 
|

|

|

|

|

|

|
|
|---|---|---|---|---|---|---|---|---|
| Диаграммы Коксетера |
||||||||
| Символ Шлефли |
s{2,4} | s{2,6} | s{2,8} | s{2,10} | s{2,12} | s{2,14}[англ.] | s{2,16}[англ.]... | s{2,∞}[англ.] |
| sr{2,2} |
sr{2,3} |
sr{2,4} |
sr{2,5} |
sr{2,6} |
sr{2,7} |
sr{2,8}... ... |
sr{2,∞} | |
| Нотация Конвея |
A2 = T | A3 = O | A4 | A5 | A6 | A7 | A8... | A∞ |
Тот же процесс применим для плосконосых мозаик:
| Треугольная мозаика Δ |
Усечённая треугольная мозаика tΔ |
Плосконосая треугольная мозаика htΔ = sΔ |
|---|---|---|
| {3,6} | t{3,6} | ht{3,6} = s{3,6} |

|

|

|
Примеры
[править | править код]| Пространство | Сферическое | Евклидово | Гиперболическое | |||||
|---|---|---|---|---|---|---|---|---|
| Рисунок | 
|

|

|

|

|

|

|

|
| Диаграмма Коксетера |
... | |||||||
| Символ Шлефли |
s{2,4} | s{3,4} | s{4,4} | s{5,4}[англ.] | s{6,4}[англ.] | s{7,4}[англ.] | s{8,4}[англ.] | ...s{∞,4}[англ.] |
| Пространство | Сферическая | Евклидово | Гиперболическое | |||||
|---|---|---|---|---|---|---|---|---|
| Рисунок | 
|

|

|

|

|

|

|

|
| Диаграмма Коксетере |
... | |||||||
| Символ Шлефли |
sr{2,3} | sr{3,3} | sr{4,3} | sr{5,3} | sr{6,3} | sr{7,3}[англ.] | sr{8,3}[англ.] | ...sr{∞,3}[англ.] |
| Нотация Конвея |
A3 | sT | sC или sO | sD или sI | sΗ или sΔ | |||
| Пространство | Сферическое | Евклидово | Гиперболическое | |||||
|---|---|---|---|---|---|---|---|---|
| Рисунок | 
|

|

|

|

|

|

|

|
| Диаграмма Коксетера |
... | |||||||
| Символ Шлефли |
sr{2,4} | sr{3,4} | sr{4,4} | sr{5,4}[англ.] | sr{6,4}[англ.] | sr{7,4}[англ.] | sr{8,4}[англ.] | ...sr{∞,4}[англ.] |
| Нотация Конвея |
A4 | sC или sO | sQ | |||||
Неоднородные плосконосые многогранники
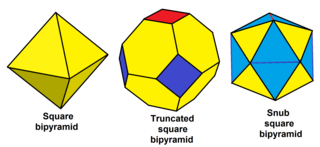
[править | править код]У неоднородных многогранников, для которых в вершины сходятся чётное число рёбер, могут быть отсечены вершины, включая некоторые бесконечные наборы, например:
|
| Плосконосая квадратная бипирамида |
|---|

|
| Плосконосая шестиугольная бипирамида |

|
| Рисунок | 
|

|

|
 ... ...
|
|---|---|---|---|---|
| Символ Шлефли |
ss{2,4} | ss{2,6} | ss{2,8} | ss{2,10}... |
| ssr{2,2} |
ssr{2,3} |
ssr{2,4} |
ssr{2,5}... |
Однородные плосконосые звёздчатые многогранники Коксетера
[править | править код]Плосконосые звёздчатые многогранники строятся по треугольнику Шварца (p q r) с рациональными зеркалами, в котором все зеркала активны и альтернированы.
 s{3/2,3/2} |
 s{(3,3,5/2)}[англ.] |
 sr{5,5/2}[англ.] |
 s{(3,5,5/3)}[англ.] |
 sr{5/2,3}[англ.] |
 sr{5/3,5}[англ.] |
 s{(5/2,5/3,3)}[англ.] |
 sr{5/3,3}[англ.] |
 s{(3/2,3/2,5/2)}[англ.] |
 s{3/2,5/3} |
Плосконосые многогранники и соты Коксетера в пространствах высокой размерности
[править | править код]В общем случае правильные 4-мерные многогранники с символом Шлефли, и диаграммой Коксетера ![]()
![]()
![]()
![]()
![]()
![]()
![]() имеет плосконосую форму с расширенным символом Шлефли и диаграммой
имеет плосконосую форму с расширенным символом Шлефли и диаграммой ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Полноусечённый многогранник = r{p,q,r}, and ![]()
![]()
![]()
![]()
![]()
![]()
![]() has snub symbol = sr{p,q,r}, and
has snub symbol = sr{p,q,r}, and ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Примеры
[править | править код]
Существует лишь один однородный плосконосый многогранник в 4-мерном пространстве, Плосконосый 24-ячейник[англ.]. Правильный двадцатичетырёхъячейник имеет символ Шлефли, и диаграмму Коксетера ![]()
![]()
![]()
![]()
![]()
![]()
![]() , а плосконосый 24-ячейник представляется символом и диаграммой диаграмма Коксетера
, а плосконосый 24-ячейник представляется символом и диаграммой диаграмма Коксетера ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Он имеет также построение с более низкой симметрией с индексом 6 как или s{31,1,1} и
. Он имеет также построение с более низкой симметрией с индексом 6 как или s{31,1,1} и ![]()
![]()
![]()
![]() , и симметрией с индексом 3 как или sr{3,3,4},
, и симметрией с индексом 3 как или sr{3,3,4}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() или
или ![]()
![]()
![]()
![]()
![]() .
.
Связанные Плосконосые 24-ячейные соты[англ.] модно рассматривать как или s{3,4,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , тело с более низкой симметрией как или sr{3,3,4,3} (
, тело с более низкой симметрией как или sr{3,3,4,3} (![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() или
или ![]()
![]()
![]()
![]()
![]()
![]()
![]() ), и с наименьшей симметрией как или s{31,1,1,1} (
), и с наименьшей симметрией как или s{31,1,1,1} (![]()
![]()
![]()
![]()
![]() ).
).
Евклидовыми сотами являются альтернированные шестиугольные пластинчатые соты[англ.], s{2,6,3} (![]()
![]()
![]()
![]()
![]()
![]()
![]() ) или sr{2,3,6} (
) или sr{2,3,6} (![]()
![]()
![]()
![]()
![]()
![]()
![]() ) или sr{2,3[3]} (
) или sr{2,3[3]} (![]()
![]()
![]()
![]()
![]() ).
).
Другими евклидовыми (равнорёберными) сотами являются альтернированные квадратные пластинчатые соты[англ.] s{2,4,4} (and ![]()
![]()
![]()
![]()
![]()
![]()
![]() ) или sr{2,41,1} (
) или sr{2,41,1} (![]()
![]()
![]()
![]()
![]() ):
):
Единственными однородными плосконосыми гиперболическими сотами являются плосконосые шестиугольные мозаичные соты, s{3,6,3} и ![]()
![]()
![]()
![]()
![]()
![]()
![]() , которые можно построить также как Альтернированные шестиугольные мозаичные соты[англ.], h{6,3,3},
, которые можно построить также как Альтернированные шестиугольные мозаичные соты[англ.], h{6,3,3}, ![]()
![]()
![]()
![]()
![]()
![]()
![]() . It is also constructed as s{3[3,3]} and
. It is also constructed as s{3[3,3]} and ![]()
![]()
![]() .
.
Другими гиперболическими (равнорёберными) сотами являются плосконосые октаэдральные соты порядка 4[англ.], s{3,4,4} и ![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
См. также
[править | править код]| Основа | Усечение | Полное усечение | Глубокое усечение[англ.] | Двойствен- ность |
Растяжение | Всеусечение[англ.] | Альтернация[англ.] | ||
|---|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

|

| ||
| t0{p, q} {p, q} |
t01{p,q}[англ.] t{p, q} |
t1{p,q} r{p, q} |
t12{p,q}[англ.] 2t{p, q} |
t2{p, q} 2r{p, q} |
t02{p,q}[англ.] rr{p, q} |
t012{p,q}[англ.] tr{p, q} |
ht0{p,q}[англ.] h{q, p} |
ht12{p,q} s{q, p} |
ht012{p,q} sr{p, q} |
Примечания
[править | править код]- ↑ Kepler, Harmonices Mundi, 1619
- ↑ Conway, 2008, с. 287.
- ↑ Conway, 2008, с. 401.
Литература
[править | править код]- H. S. M. Coxeter, M. S. Longuet-Higgins, J. C. P. Miller. Uniform polyhedra // Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. — The Royal Society, 1954. — Т. 246, вып. 916. — С. 401–450. — ISSN 0080-4614. — doi:10.1098/rsta.1954.0003. — .
- Coxeter, H.S.M. 8.6 Partial truncation, or alternation // Regular Polytopes. — 3rd. — 1973. — С. 154–156. — ISBN 0-486-61480-8.
- Coxeter. Tables I and II: Regular polytopes and honeycombs // Regular Polytopes[англ.]. — 3rd. ed.. — Dover Publications, 1973. — С. 154–156. — ISBN 0-486-61480-8.
- H.S.M. Coxeter. Kaleidoscopes: Selected Writings of H.S.M. Coxeter / F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss. — Wiley-Interscience Publication, 1995. — ISBN 978-0-471-01003-6.
- (Paper 17) Coxeter, The Evolution of Coxeter–Dynkin diagrams, [Nieuw Archief voor Wiskunde 9 (1991) 233–248]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
- H.S.M. Coxeter. Chapter 3: Wythoff's Construction for Uniform Polytopes // The Beauty of Geometry: Twelve Essays. — Dover Publications, 1999. — ISBN 0-486-40919-8.
- N.W. Johnson. Uniform Polytopes. — 1991. — (Manuscript).
- N.W. Johnson. The Theory of Uniform Polytopes and Honeycombs. — University of Toronto, 1966. — (Ph.D. Dissertation).
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. The Symmetries of Things. — 2008. — ISBN 978-1-56881-220-5.
- Weisstein, Eric W. Snubification (англ.) на сайте Wolfram MathWorld.
- Richard Klitzing. Snubs, alternated facetings, and Stott–Coxeter–Dynkin diagrams // Symmetry: Culture and Science. — 2010. — Т. 21, вып. 4. — С. 329–344.
Для улучшения этой статьи желательно:
|