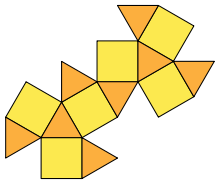
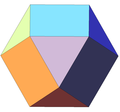
Кубооктаэдр

Кубооктаэдр
(вращающаяся модель, 3D-модель)
Тип	архимедово тело
Свойства	выпуклый, изогональный, квазиправильный
Комбинаторика
Элементы	14 граней 24 ребра 12 вершин Χ = 2
Грани	8 треугольников 6 квадратов
Конфигурация вершины	3.4.3.4
Двойственный многогранник	ромбододекаэдр
Вершинная фигура
Развёртка
Классификация
Обозначения	aC, aaT
Символ Шлефли	r{3,4}, rr{3,3}
Группа симметрии	Oh (октаэдрическая)
Медиафайлы на Викискладе

Кубоокта́эдр или кубокта́эдр — полуправильный многогранник (архимедово тело) с 14 гранями, составленный из 8 правильных треугольников и 6 квадратов.

В каждой из его 12 одинаковых вершин сходятся две квадратных грани и две треугольных. Телесный угол при вершине равен $\arccos \left(-{\frac {7}{9}}\right)\approx 0{,}78\pi .$

Кубооктаэдр имеет 24 ребра равной длины. Двугранный угол при любом ребре одинаков и равен $\arccos \left(-{\frac {\sqrt {3}}{3}}\right)\approx 125{,}26^{\circ }.$

Кубооктаэдр можно получить из куба, «срезав» с него 8 правильных треугольных пирамид; либо из октаэдра, «срезав» с него 6 квадратных пирамид; либо как пересечение имеющих общий центр куба и октаэдра.

Иллюстрация Леонардо да Винчи к трактату Луки Пачоли «О божественной пропорции» (1509)

В координатах

Кубооктаэдр с длиной ребра ${\sqrt {2}}$ можно расположить в декартовой системе координат так, чтобы координаты его вершин были всевозможными перестановками чисел $(0;\;\pm 1;\;\pm 1).$

Начало координат $(0;\;0;\;0)$ будет при этом центром симметрии многогранника, а также центром его описанной и полувписанной сфер.

Метрические характеристики

Если кубооктаэдр имеет ребро длины $a$, его площадь поверхности и объём выражаются как

$S=\left(6+2{\sqrt {3}}\right)a^{2}\approx 9{,}4641016a^{2},$

$V={\frac {5{\sqrt {2}}}{3}}\;a^{3}\approx 2{,}3570226a^{3}.$

Радиус описанной сферы (проходящей через все вершины многогранника) при этом будет равен

$R=a=1{,}0000000a,$

радиус полувписанной сферы (касающейся всех рёбер в их серединах) —

$\rho ={\frac {\sqrt {3}}{2}}\;a\approx 0{,}8660254a.$

Вписать в кубооктаэдр сферу — так, чтобы она касалась всех граней, — невозможно. Радиус наибольшей сферы, которую можно поместить внутри кубооктаэдра с ребром $a$ (она будет касаться только всех квадратных граней в их центрах), равен

$r_{4}={\frac {\sqrt {2}}{2}}\;a\approx 0{,}7071068a.$

Расстояние от центра многогранника до любой треугольной грани превосходит $r_{4}$ и равно

$r_{3}={\frac {\sqrt {6}}{3}}\;a\approx 0{,}8164966a.$

Звёздчатые формы

Кубооктаэдр образует звёздчатые формы:

• 

  Исходный многогранник

• 

  Первая звёздчатая форма

• 

  Вторая звёздчатая форма

• 

  Третья звёздчатая форма

• 

  Четвёртая звёздчатая форма

Заполнение пространства

Одними только кубооктаэдрами замостить трёхмерное пространство без промежутков и наложений нельзя, но это можно сделать с помощью кубооктаэдров вместе с другими многогранниками:

• 

  Кубооктаэдры и октаэдры

• 

  Ромбокубоктаэдры, кубооктаэдры и кубы

• 

  Усечённые октаэдры, усечённые тетраэдры и кубооктаэдры

• 

  Растянутые ромбододекаэдры, кубооктаэдры, октаэдры и треугольные призмы

В природе и культуре

Одним из символов компьютерной игры Elite стала космическая станция в форме кубооктаэдра с люком на квадратной грани. Впоследствии её внесли и в Elite: Dangerous.

• 

  Кристалл синтетического алмаза под электронным микроскопом

• 

  Вариант кубика Рубика

• 

Литература

• М. Веннинджер. Модели многогранников. — Мир, 1974.
• Многоугольники и многогранники // Энциклопедия элементарной математики. Книга четвёртая. Геометрия / Под ред. П. С. Александрова, А. И. Маркушевича, А. Я. Хинчина. — М.: Государственное издательство физико-математической литературы, 1963. — С. 382—447. — 568 с. — 20 000 экз.
• Л. А. Люстерник. Выпуклые фигуры и многогранники. — М.: Государственное издательство технико-теоретической литературы, 1956.

Ссылки

• Weisstein, Eric W. Кубооктаэдр (англ.) на сайте Wolfram MathWorld.