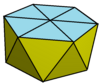
Шестиугольная антипризма

Однородная шестиугольная антипризма
Тип	Призматический однородный многогранник
Элементы	Граней 14, рёбер 24, вершин 12
Эйлерова характеристика	$\chi$ = 2
Граней по числу сторон	12{3}+23{6}
Символ Витхоффа	| 2 2 6
Символ Шлефли	s{2, 12} sr{2, 6}
Диаграммы Коксетера
Группа симметрии	D6d, [2+б 12], (2*6), 24 порядка
Группа вращений	D6, [6,2]+, (622), 12 порядка
Обозначения	U77(d)
Свойства	выпуклый
Вершинная фигура 3.3.3.6	Шестиугольный трапецоэдр (двойственный многогранник)

Шестиугольная антипризма — 4-я в бесконечном множестве антипризм, образованная чётным числом треугольных сторон между двумя шестиугольными сторонами.

Если все грани правильные, многогранник является полуправильным.

Связанные многогранники

Шестиугольные грани могут быть заменены копланарными треугольниками (находящимися в одной плоскости), что приведёт к невыпуклому многограннику с 24 правильными треугольниками.

Однородные шестиугольные диэдральные сферические многогранники

Симметрия: [6,2], (*622)							[6,2]+, (622)	[6,2+], (2*3)
{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{2,6}	tr{6,2}	sr{6,2}	s{2,6}
Двойственные им многогранники
V62	V122	V62	V4.4.6	V26	V4.4.6	V4.4.12	V3.3.3.6	V3.3.3.3

Семейство однородных антипризм n.3.3.3

Многогранник
Мозаика
Конфигурация	V2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	...∞.3.3.3

Ссылки

• Weisstein, Eric W. Antiprism (англ.) на сайте Wolfram MathWorld.
• Hexagonal Antiprism: Interactive Polyhedron model
• Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra
  • VRML model
  • Conway Notation for Polyhedra Try: "A6"