Метод неделимых
Метод неделимых — возникшее в конце XVI века наименование совокупности приёмов, предназначенных для вычисления площадей геометрических фигур или объёмов геометрических тел[1]. Идея метода для плоских фигур состояла в том, чтобы разделить эти фигуры на фигуры нулевой ширины («неделимые», обычно они представляют собой параллельные отрезки), которые потом «собираются» без изменения их длины и образуют другую фигуру, площадь которой уже известна (см. примеры ниже). Вычисление объёма пространственных тел происходит аналогично, только они разделяются не на отрезки, а на «неделимые» плоские фигуры[2]. Формализация этих приёмов во многом определила в дальнейшем зарождение и развитие интегрального исчисления.
Наиболее полное выражение и теоретическое обоснование метод неделимых получил в работе итальянского математика Бонавентуры Кавальери «Геометрия неделимых непрерывных, выведенная новым способом» (лат. Geometria indivisibilibus continuorum nova quadam ratione promota, 1635 год)[3][4]
Пример и критика[править | править код]
Сам по себе метод неделимых — это набор приёмов без чёткого описания. Поэтому лучше начать со следующего примера, известного уже Архимеду.


Вычислим площадь круга радиуса . Формула для длины окружности считается известной.
Разобьём круг на бесконечно малые кольца. Рассмотрим также треугольник с длиной основания и высотой , который тоже разобьём сечениями параллельно основанию. Каждому кольцу радиуса и длины можно сопоставить одно из сечений треугольника той же длины . Тогда, по принципу Кавальери, площади круга и треугольника равны. Площадь треугольника находится как произведение длины его основания на половину высоты:
Парадокс Кавальери[править | править код]
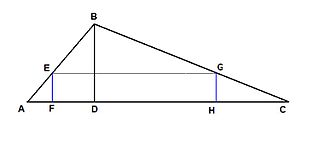
Математики сразу указали на возможность ошибочного применения принципа неделимых; один из таких примеров привёл сам Кавальери в письме к Торричелли (см. рисунок). Треугольники ABD и BCD состоят из вертикальных неделимых, причём каждой неделимой левого треугольника (EF) можно взаимно-однозначно сопоставить неделимую той же длины (GH) правого треугольника. Отсюда, согласно основному принципу, можно сделать ошибочный вывод, что площади треугольников равны[5]. Тем не менее, ясного правила для избежания ошибок Кавальери не дал.
Принцип Кавальери[править | править код]

Кавальери в своём трактате «Геометрия неделимых непрерывных, выведенная новым способом» сформулировал теоретические основы метода неделимых следующим образом:
Фигуры относятся друг к другу, как все их линии, взятые по любой регуле [базе параллельных], а тела — как все их плоскости, взятые по любой регуле.
Если два тела имеют одинаковую высоту, и если сечения тел, равноудалённые и параллельные плоскости, на которой те покоятся, всегда останутся в заданном отношении, то и объёмы тел останутся в этом отношении.
В современном виде:
- Для плоскости
- Площади двух фигур с равными по длине хордами всех их общих секущих, параллельных прямой, по одну сторону от которой они лежат, равны.
- Для пространства
- Объёмы двух тел над плоскостью, с равными по площади сечениями всех общих секущих их плоскостей, параллельных данной плоскости, равны.
Принцип Кавальери явился одним из первых шагов на пути к интегральному исчислению. В частности, используя обозначения бесконечно малых, Кавальери доказал теорему, эквивалентную современной формуле
Современными теоремами, обобщающими принцип Кавальери, являются формула коплощади и теорема Тонелли — Фубини.
Пример[править | править код]

Идея нахождения объёмов в этом примере восходит к Архимеду.
Вычислим объём полушария радиуса r. Формулы для площади круга, а также для объёма конуса и цилиндра считаются известными.
Проведём сечения полушария плоскостями, параллельными его основанию. Полушарие разобьётся на бесконечно малые круги (см. рисунок). На высоте h площадь сечения будет равна , или (по теореме Пифагора) .
Далее рассмотрим круговой цилиндр высоты r, с радиусом основания тоже r, из которого вырезан конус остриём вниз. Рассечём и это тело параллельно основанию. В сечении на высоте h получится кольцо площадью . Замечаем, что эта площадь такая же, как и для полушария.
Следовательно, по принципу Кавальери, объёмы обоих тел равны. Объём тела, изображённого справа на рис. 3, равен
Вывод: объём полного шара (двух полушарий) равен
История[править | править код]
Уже Архимед в своих исследованиях рассекал пространственное тело параллельными плоскостями и представлял это тело как своего рода альбом, объединение таких сечений (инфинитезимальное разложение, то есть разложение на бесконечно малые элементы). Здесь возможно влияние атомистов с их «неделимыми». Однако Архимед считал обязательным передоказывать результаты, полученные с помощью метода неделимых, строгим методом исчерпывания. Европейские математики, начиная с XVI века, тоже применяли метод исчерпывания для проведения квадратур (вычисления площадей) и определения центров тяжести.
Новую жизнь методу неделимых дал Кеплер в своей книге «Новая стереометрия винных бочек» (XVII век).[6] В труде «Новая астрономия» Кеплер часто использует понятие «неделимых», в том числе при формулировке своих трёх законов движения планет; например, вместо площади он упоминал «сумму радиус-векторов».
Возможно, независимо этот метод развивал Роберваль.[7]
Наиболее ярким и влиятельным представителем «геометрии неделимых» был Кавальери. В его изложении инфинитезимальные представления Кеплера обрели вид общих вычислительных приёмов. Мощь и относительная простота нового метода произвели чрезвычайно сильное впечатление на математиков. Целые поколения, от Валлиса до Лейбница, учились у Кавальери. Торричелли назвал метод неделимых «царской дорогой» в геометрии.
Галилей был знаком с методом неделимых, однако отчётливо видел его слабые и опасные стороны. В переписке и последних трудах он размышляет о сущности бесконечности, показывает, что бесконечное множество может быть равносчётно своей части, имеющей меньшую меру, так что рассуждения о неделимых плохо обоснованы. Тем не менее он сам фактически использовал неделимые при исследовании равноускоренного движения[8].
Валлис, ознакомившись с методом Кавальери по книге Торричелли, решил провести его алгебраизацию. Вместо геометрического преобразования сечений он строит в «Арифметике бесконечных» (1656 год) числовые ряды, которые мы сейчас называем интегральными суммами, и находит эти суммы.
Независимо от Валлиса и лет на 30 раньше эти интегралы вычислили Ферма и Роберваль. В посмертно опубликованном сочинении Ферма виртуозно применяет такие приёмы, как интегрирование по частям и замена переменных, что позволило ему вычислить множество сложных интегралов от дробно-рациональных функций и от многочленов с дробными степенями.
Мемуар Ферма получил широкую известность, так как он почти полностью покрывает результаты Кавальери, но при этом изложенные методы существенно компактнее и понятнее. Кроме того, интегральные суммы оказались применимы к задачам, недоступным для метода Кавальери — например, спрямление (измерение дуги) кривой. Роберваль исследовал спираль Архимеда, Ферма и Торричелли в 1640-е годы — параболы и спирали высших порядков. Жиль Роберваль (1634—1636 гг.) и Кристофер Рен (1658 год) спрямили циклоиду.
Учитывая уязвимость для критики тех открытий, которые получены с помощью метода неделимых, многие математики (Ферма, Паскаль, Барроу и др.) отмечали в своих работах, что все их результаты могут быть без труда передоказаны строгими методами древних. Барроу, правда, сделал к этой оговорке ироничное добавление: «только зачем?».[9]
Декарт использовал инфинитезимальные методы в своей «Оптике», но в целом старался не углубляться в эту область. В трактате «Геометрия» он высказал мнение, что спрямление алгебраических линий невозможно. Это утверждение было опровергнуто лишь через двадцать лет: в 1650-х годах сразу четыре математика, включая Ферма и Гюйгенса, дали спрямление полукубической параболы. Впрочем, и сам Декарт успешно спрямил, правда, не алгебраическую, а трансцендентную кривую — логарифмическую спираль, длина дуги которой, считая от полюса, пропорциональна радиус-вектору конца дуги — свойство, которое знал и Торричелли.
Идея Валлиса — алгебраизация метода бесконечно малых — достигла высшего развития после открытия математического анализа Ньютоном и Лейбницем. В своих «Началах» Ньютон дал первый набросок общей теории пределов (11 лемм), при этом он не постулирует аналог принципа Кавальери, а строго его доказывает (следствие из леммы IV):
Если вообще две какого угодно рода величины будут разделены на одинаковое число частей и, при бесконечном возрастании числа их и уменьшении каждой из них, отношение их соответственно друг к другу, то есть первой к первой, второй ко второй и т. д., остаётся постоянным, то и самые величины будут находиться в этом же отношении.
Здесь неделимые заменены на переменные, величина которых стремится к нулю; при этом «парадокса Кавальери» уже не может возникнуть, поскольку отношение сравниваемых в парадоксе величин (ширины малых четырёхугольников в разбиении) не равно единице.
После создания анализа метод неделимых представлял уже только исторический интерес. Однако ещё более века, до работ Коши, обоснование анализа бесконечно малых было столь же неубедительным, как и у метода неделимых.
См. также[править | править код]
Примечания[править | править код]
- ↑ Неделимых метод // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3. Архивировано 16 октября 2013 года.
- ↑ Кавальери принцип // Казахстан. Национальная энциклопедия. — Алматы: Қазақ энциклопедиясы, 2005. — Т. III. — ISBN 9965-9746-4-0. (CC BY-SA 3.0)
- ↑ История математики, том II, 1970, с. 175.
- ↑ Bonaventura Cavalieri (Italian mathematician) Архивная копия от 11 июня 2015 на Wayback Machine — Encyclopedia Britannica.
- ↑ Хрестоматия по истории математики, 1977, с. 51.
- ↑ Кеплер, Иоганн. Новая стереометрия винных бочек Архивная копия от 8 февраля 2013 на Wayback Machine. — М.—Л.: ГТТИ, 1935. — 360 с.
- ↑ Florian Cajori, A History of Mathematics, 5th edition, 1991, p. 162.
- ↑ Хрестоматия по истории математики, 1977.
- ↑ Бурбаки Н. Архитектура математики. Очерки по истории математики. — М.: Иностранная литература, 1963. — С. 177.
Литература[править | править код]
- Лурье С. Я. Теория бесконечно-малых у древних атомистов. — М.—Л.: Изд. АН СССР, 1935.
- Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
- Хрестоматия по истории математики. Математический анализ. Теория вероятностей / Под ред. А. П. Юшкевича. — М.: Просвещение, 1977. — 224 с.
- Шан-Гирей А., Флоринский Г. Объем шара (способ Кавалериуса) // В.О.Ф.Э.М.. — 1889. — № 62. — С. 32—34.











