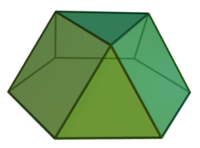
Трёхскатный купол

Трёхскатный купол
Трёхскатный купол
Тип	многогранник Джонсона J2 - J3 - J4
Свойства	выпуклый многогранник
Комбинаторика
Элементы	15 рёбер 9 вершин
Грани	1 + 3 треугольника 3 квадрата 1 шестиугольник
Конфигурация вершины	6(3.4.6) 3(3.4.3.4)
Двойственный многогранник	dual of triangular cupola[d]
Развёртка
Классификация
Символ Шлефли	{3}||t{3}
Группа симметрии	C3v

Трёхскатный купол — один из многогранников Джонсона (J₃ = (по Залгаллеру) М₄). Купол можно рассматривать как половину кубооктаэдра.

Многогранник Джонсона — один из строго выпуклых многогранников, имеющих правильные грани, но не являющийся однородным (то есть он не является правильным многогранником, архимедовым телом, призмой или антипризмой). Многогранники названы именем Нормана Джонсона, который первым перечислил эти многогранники в 1966 году.

Формулы

Следующие формулы для объёма и площади поверхности могут быть использованы, если все грани правильные с длиной стороны a:

$V=\left({\frac {5}{3{\sqrt {2}}}}\right)a^{3}\approx 1,17851...a^{3}$

$A=\left(3+{\frac {5{\sqrt {3}}}{2}}\right)a^{2}\approx 7,33013...a^{2}$

Двойственный многогранник

Двойственный многогранник трёхскатного купола имеет 6 треугольных и 3 дельтоидных гранией:

Двойственный многогранник трёхскатного купола	Развёртка двойственного многогранника

Связанные многогранники и соты

Трёхскатный купол может быть увеличен на 3 квадратные пирамиды, оставив без изменения смежные грани. Полученный многогранник не является многогранником Джонсона, поскольку его грани находятся в одной плоскости. Если слить эти компланарные треугольники, получится другой купол с гранями в виде равнобедренных трапеций. Если все треугольники сохранить, а шестиугольник в основании разбить на 6 треугольников, получится компланарный дельтаэдр с 22 гранями.

Дельтаэдр

Трёхскатный купол может образовать соты с квадратными пирамидами и/или октаэдрами таким же образом, каким октаэдры и кубооктаэдры могут заполнять пространство.

Семейство куполов с правильными многоугольниками существует до n=5 включительно.

Семейство выпуклых куполов

n	2	3	4	5	6
Название	{2} || t{2}	{3} || t{3}	{4} || t{4}	{5} || t{5}	{6} || t{6}
Купол	Диагональный купол	Трёхскатный купол	Четырёхскатный купол	Пятискатный купол	Шестискатный купол (плоский)
Связанные однородные многогранники	Треугольная призма	Кубооктаэдр	Ромбокубо- октаэдр	Ромбоикосо- додекаэдр	Ромботри- шестиугольная мозаика

Литература

• Norman W. Johnson. Convex polyhedra with regular faces // Canadian Journal of Mathematics. — 1966. — Т. 18. — С. 169–200. — doi:10.4153/cjm-1966-021-8.

Ссылки

• Triangular cupola  (неопр.). MathWorld. Eric W. Weisstein.