Многогранник Джонсона

Многогранник Джонсона или тело Джонсона — это выпуклый многогранник, каждая грань которого является правильным многоугольником и при этом он не является ни платоновым телом, ни архимедовым, ни призмой, ни антипризмой. Всего существует 92 тела Джонсона.
Примером тела Джонсона служит пирамида с квадратным основанием и сторонами в виде правильных треугольников (J1(М2). Она имеет 1 квадратную грань и 4 треугольных.
Как и во всяком строго выпуклом теле, у этих многогранников к каждой вершине примыкает по меньшей мере три грани и сумма их углов (прилегающих к вершине) меньше 360º. Поскольку правильные многоугольники имеют углы по меньшей мере в 60º, максимум пять граней могут прилегать к вершине. Пятиугольная пирамида (J2) является примером, в котором имеется вершина пятого порядка (то есть с пятью гранями).
Хотя нет явного ограничения на правильные многоугольники, которые могут служить гранями тел Джонсона, на самом деле грани могут иметь только 3, 4, 5, 6, 8 или 10 сторон, причём треугольные грани (не менее четырёх) имеются у любого тела Джонсона.
Из тел Джонсона удлинённый четырёхскатный повёрнутый бикупол (J37), который называют также псевдоромбокубооктаэдром[1], единственный обладает свойством локальной вершинной однородности — в каждой вершине находятся 4 грани и их расположение одинаково — 3 квадрата и 1 треугольник. Однако тело вершинно транзитивным не является, поскольку обладает различной изометрией в различных вершинах, что и делает его телом Джонсона, а не архимедовым телом.
История[править | править код]
В 1966 году Норман Джонсон опубликовал список, в котором присутствовали все 92 тела, и дал им названия и номера. Он высказал гипотезу, что их только 92, то есть других нет.
Ранее, в 1946 году Л. Н. Есаулова прислала А. Д. Александрову письмо, в котором доказала, что правильногранных многогранников (кроме 5 правильных многогранников, 13 полуправильных и двух бесконечных серий (призмы и антипризм) может существовать лишь конечное число. В 1961 году Александров передал это письмо В. А. Залгаллеру, возможно из-за заметки Джонсона 1960 года[2].
В 1967 году Виктор Залгаллер опубликовал доказательство того, что список Джонсона полон. К решению была привлечена группа школьников школы № 239. Полное доказательство заняло около 4 лет с привлечением компьютерной техники. В доказательстве также существенно использовалась теорема Александрова о выпуклых многогранниках.
Терминология[править | править код]
Названия тел Джонсона имеют большую описательную способность. Большинство этих тел можно построить из нескольких тел (пирамид, куполов и ротонд), добавляя платоновы и архимедовы тела, призмы и антипризмы.
- Би- означает, что две копии тел соединены по основаниям. Для куполов и ротонд они могут быть соединены по граням одного типа (прямые) или по разным (повёрнутые). Октаэдр, например, является квадратной бипирамидой, кубооктаэдр — повёрнутым треугольным бикуполом, а икосододекаэдр — повёрнутой пятиугольной биротондой.
- Удлинённый означает, что к телу присоединена призма или она вставлена между двумя частями тела. Ромбокубооктаэдр, например, является удлинённым квадратным прямым бикуполом.
- Скрученно удлинённый означает, что к телу присоединена антипризма или она вставлена между двумя частями тела. Икосаэдр, например, является скрученно удлинённой пятиугольной бипирамидой.
- Наращённый означает, что пирамида или купол присоединён к грани тела.
- Отсечённый означает, что пирамида или купол отрезан от тела.
- Скрученный означает, что купол, принадлежащий многограннику, повёрнут таким же образом, как в повёрнутых бикуполах.
Последние три операции — наращение, отсечение и поворот — могут быть осуществлены более одного раза на достаточно больших многогранниках. Для операций, осуществлённых два раза, добавляется дважды. (Дважды скрученное тело имеет два повёрнутых купола.) Для операций, осуществлённых три раза, добавляется трижды. (У трижды отсечённого тела удалены три пирамиды или купола.)
Иногда слова дважды недостаточно. Необходимо отличать тела, в которых изменены две противоположные грани от тел, в которых изменены другие грани. Когда изменённые грани параллельны, в название добавляется противоположно. (Дважды противоположно наращённое тело имеет две параллельные грани (противоположные) с добавленными телами.) Если же изменения касаются граней, не являющихся противоположными, в название добавляется косо. (Дважды косо наращённое тело имеет две грани с добавленными телами, но грани не противоположны.)
Несколько названий происходят от многоугольников, из которых собрано тело Джонсона.
- Если определить месяц как группу из двух треугольников, присоединённых к квадрату, слово клинокорона соответствует клиновидной короноподобной группе, образованной двумя месяцами. Слово двуклиноид или двуклинник означает две таких группы.
В данной статье используются названия из статьи Залгаллера[3]. Вместе с номерами многогранников, данными Джонсоном, в скобках приводится составной номер из статьи Залгаллера. В этом составном номере
- Пn обозначает призму с n-угольным основанием.
- Аn обозначает антипризму с n-угольным основанием.
- Мn обозначает тело с индесом n (то есть в этом случае тело строится на основе другого тела).
- Подчёркивание означает поворот тела
Замечание: Мn не совпадает с Jn. Так, квадратная пирамида J1(М2) имеет индекс 1 у Джонсона и индекс 2 у Залгаллера.
Список[править | править код]
Пирамиды[править | править код]
Первые два тела Джонсона, J1 и J2, являются пирамидами. Треугольная пирамида является правильным тетраэдром, так что не является телом Джонсона.
| Правильные | J1(М2) | J2(М3) |
|---|---|---|
| Треугольная пирамида (Тетраэдр) |
Квадратная пирамида | Пятиугольная пирамида |

|

|

|

|

|

|
Куполы и ротонды[править | править код]
Следующие четыре многогранника являются тремя куполами и одной ротондой.
| Куполы | Ротонды | |||
|---|---|---|---|---|
| Однородные | J3(М4) | J4(М5) | J5(М6) | J6(М9) |
| Треугольная призма | Трёхскатный купол | Четырёхскатный купол | Пятискатный купол | Пятискатная ротонда |

|

|

|

|

|

|

|
|

| |
| Связанные однородные многогранники | ||||
| Кубооктаэдр | Ромбокубооктаэдр | Ромбоикосододекаэдр | Икосододекаэдр | |

|

|

|

| |
Удлинённые и скрученно удлинённые пирамиды[править | править код]
Следующие пять многогранников Джонсона являются удлинёнными и скручено удлинёнными пирамидами. Они представляют собой склеивание двух многогранников. В случае скрученно удлинённой треугольной пирамиды три пары смежных треугольников копланарны, так что тело не является многогранником Джонсона.
| Удлинённые пирамиды[англ.] (или наращённые призмы) |
Скрученно удлинённые пирамиды[англ.] (или наращённые антипризмы) | ||||
|---|---|---|---|---|---|
| J7(М1+П3) | J8(М2+П4) | J9(М3+П5) | Копланарная | J10(М2+А4) | J11(М3+А5) |
| Удлинённая треугольная пирамида | Удлинённая четырёхугольная пирамида | Удлинённая пятиугольная пирамида | Скрученно удлинённая треугольная пирамида | Скрученно удлинённая четырёхугольная пирамида | Скрученно удлинённая пятиугольная пирамида |
| Наращённая треугольная призма | Наращённый куб | Наращённая пятиугольная призма | Наращённый октаэдр | Наращённая квадратная антипризма | Наращённая пятиугольная антипризма |

|

|

|

|

|

|

|

|

|

|

| |
| Получено из многогранников | |||||
| тетраэдр Треугольная призма |
Квадратная пирамида куб |
Пятиугольная пирамида пятиугольная призма |
тетраэдр октаэдр |
Квадратная пирамида квадратная антипризма |
пятиугольная пирамида пятиугольная антипризма |
Бипирамиды[править | править код]
Следующими многогранниками Джонсона являются бипирамиды, удлинённые бипирамиды[англ.] и скрученно удлинённые бипирамиды[англ.]:
| Бипирамиды | Удлинённые бипирамиды[англ.] | Скрученно удлинённые бипирамиды[англ.] | ||||||
|---|---|---|---|---|---|---|---|---|
| J12(2М1) | Правильная | J13(2М3) | J14(М1+П3+М1) | J15(М2+П4+М2) | J16(М3+П5+М3) | Копланарная | J17(М2+А4+М2) | Правильные |
| Треугольная бипирамида | квадратная бипирамида (октаэдр) |
Пятиугольная бипирамида | Удлинённая треугольная бипирамида | Удлинённая четырёхугольная бипирамида | Удлинённая пятиугольная бипирамида | Скрученно удлинённая треугольная бипирамида (ромбоэдр) |
Скрученно удлинённая четырёхугольная бипирамида | Скрученно удлинённая пятиугольная бипирамида (икосаэдр) |

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
||
| Получено из многогранников | ||||||||
| тетраэдр | Квадратная пирамида | Пятиугольная пирамида | тетраэдр Треугольная призма |
Квадратная пирамида куб |
Пятиугольная пирамида пятиугольная призма |
тетраэдр октаэдр |
Квадратная пирамида Четырёхугольная антипризма[англ.] |
Пятиугольная пирамида Пятиугольная антипризма |
Удлинённые куполы и ротонды[править | править код]
Бикуполы[править | править код]
Повёрнутые треугольные бикуполы являются полуправильными многогранниками (в данном случае — архимедовыми телами), так что они не принадлежат классу многогранников Джонсона.
| Прямые куполы | Повёрнутые куполы | ||||||
|---|---|---|---|---|---|---|---|
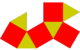
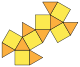
| Копланарный | J27(2М4) | J28(2М5) | J30(2М6) | J26(П3+П3) | Полуправильный | J29(М5+М5) | J31(М6+М6) |
| Двускатный прямой бикупол | Трёхскатный прямой бикупол | Четырёхскатный прямой бикупол | Пятискатный прямой бикупол | Двускатный повёрнутый бикупол (гиробифастигиум) |
Треугольный повёрнутый бикупол (кубооктаэдр) |
Четырёхскатный повёрнутый бикупол | Пятискатный повёрнутый бикупол |

|

|

|

|

|

|
||

|

|
|
|
|

|

| |
| Получены из многогранников | |||||||
Куполоротонды и биротонды[править | править код]
| Куполоротонды | Биротонды | ||
|---|---|---|---|
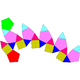
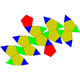
| J32(М6+М9) | J33(М6+М9) | J34(2М9) | Полуправильная |
| Пятискатная прямая куполоротонда | Пятискатная повёрнутая куполоротонда | Пятискатная прямая биротонда | Пятискатная повёрнутая биротонда икосододекаэдр |

|

|

|

|
|

|
|

|
| Получены из многогранников | |||
| Пятискатный купол Пятискатная ротонда |
Пятискатная ротонда | ||
Удлинённые бикуполы[править | править код]
| Удлинённые прямые бикуполы[англ.] | Удлинённые повёрнутые бикуполы[англ.] | ||||||
|---|---|---|---|---|---|---|---|
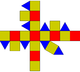
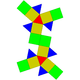
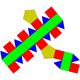
| Копланарный | J35(М4+П6+М4) | Полуправильный | J38(М6+П10+М6) | Копланарный | J36(М4+П6+М4) | J37(М5+П8+М5) | J39(М6+П10+М6) |
| Удлинённый двускатный прямой бикупол | Удлинённый трёхскатный прямой бикупол | Удлинённый квадратный прямой бикупол (ромбокубооктаэдр) |
Удлинённый пятискатный прямой бикупол | Удлинённый двухскатный повёрнутый бикупол | Удлинённый трёхскатный повёрнутый бикупол | Удлинённый четырёхскатный повёрнутый бикупол | Удлинённый пятискатный повёрнутый бикупол |

|

|

|

|

|

|

|

|

|
|

|
|

|
| ||
Удлинённые куполоротонды и биротонды[править | править код]
| Удлинённые куполоротонды | Удлинённые биротонды | ||
|---|---|---|---|
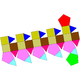
| J40(М6+П10+М9) | J41(М6+П10+М9) | J42(М9+П10+М9) | J43(М9+П10+М9) |
| Удлинённая пятискатная прямая куполоротонда | Удлинённая пятискатная повёрнутая куполоротонда | Удлинённая пятискатная прямая биротонда | Удлинённая пятискатная повёрнутая биротонда |

|

|

|

|

|
|

|

|
Скрученно удлинённые бикуполы, куполоротонды и биротонды[править | править код]
Следующие тела Джонсона имеют две хиральные формы.
| Скрученно удлинённые бикуполы[англ.] | Скрученно удлинённая куполоротонда | Скрученно удлинённая биротонда | |||
|---|---|---|---|---|---|
| Невыпуклый | J44(М4+А6+М4) | J45(М5+А8+М5) | J46(М6+А10+М6) | J47(М6+А10+М9) | J48(М9+А10+М9) |
| Скрученно удлинённый двускатный бикупол | Скрученно удлинённый трёхскатный бикупол | Скрученно удлинённый четырёхскатный бикупол | Скрученно удлинённый пятискатный бикупол | Скрученно удлинённая пятискатная куполоротонда | Скрученно удлинённая пятискатная биротонда |

|

|

|

|

|

|

|

|

|

|

| |
| Получены из многогранников | |||||
| Треугольная призма Четырёхугольная антипризма |
Трёхскатный купол Шестиугольная антипризма |
Четырёхскатный купол Восьмиугольная антипризма[англ.] |
Пятискатный купол Десятиугольная антипризма[англ.] |
Пятискатный купол Пятискатная ротонда Десятиугольная антипризма[англ.] |
Пятискатная ротонда Десятиугольная антипризма[англ.] |
Наращённые треугольные призмы[править | править код]
| J7(М1+ П3) (повторно) |
J49(П3+М2) | J50(П3+2М2) | J51(П3+3М2) | |
|---|---|---|---|---|
| Удлинённая треугольная пирамида | Наращённая треугольная призма | Дважды наращённая треугольная призма | Трижды наращённая треугольная призма | |

|

|

|

| |

|

|

|

| |
| Получены из многогранников | ||||
| Треугольная призма тетраэдр |
Треугольная призма Квадратная пирамида | |||
Наращённые пятиугольные и шестиугольные призмы[править | править код]
| Наращённые пятиугольные призмы | Наращённые шестиугольные призмы | ||||
|---|---|---|---|---|---|
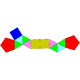
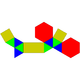
| J52(П5+М2) | J53(П5+2М2) | J54(П6+М2) | J55(М2+П6+М2) | J56(П6+2М2) | J57(П6+3М2) |
| Наращённая пятиугольная призма | Дважды наращённая пятиугольная призма | Наращённая шестиугольная призма | Дважды противоположно наращённая шестиугольная призма | Дважды косо наращённая шестиугольная призма | Трижды наращённая шестиугольная призма |

|

|

|

|

|

|

|
|

|
|

|

|
| Получены из многогранников | |||||
| Пятиугольная призма Квадратная пирамида |
Шестиугольная призма Квадратная пирамида | ||||
Наращённые додекаэдры[править | править код]
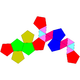
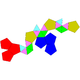
| Правильный | J58(М15+М3) | J59(М3+М15+М3) | J60(М15+2М3) | J61(М15+3М3) |
|---|---|---|---|---|
| Додекаэдр | Наращённый додекаэдр | Дважды противоположно наращённый додекаэдр | Дважды косо наращённый додекаэдр | Трижды наращённый додекаэдр |

|

|

|

|

|

|

|
|
| |
| Получены из многогранников | ||||
| Додекаэдр и пятиугольная пирамида | ||||
Отсечённые икосаэдры[править | править код]
| Правильный | J11(М3+А5) (повторно) |
J62(М7+М3) | J63(М7) | J64(М7+М1) |
|---|---|---|---|---|
| Икосаэдр | Отсечённый икосаэдр (Скрученно удлинённая пятиугольная пирамида) |
Дважды косо отсечённый икосаэдр | Трижды отсечённый икосаэдр | Наращённый трижды отсечённый икосаэдр |

|

|

|

|

|

|

|

|

| |
| Получены из многогранников | ||||
| Трижды отсечённый икосаэдр, пятиугольная пирамида и тетраэдр | ||||
Наращённые усечённые тетраэдры и кубы[править | править код]
| J65(М10+М4) | J66(М11+М5) | J67(М5+М11+М5) |
|---|---|---|
| Наращённый усечённый тетраэдр | Наращённый усечённый куб | Дважды наращённый усечённый куб |

|

|

|

|

|

|
| Получены из многогранников | ||
| Усечённый тетраэдр Трёхскатный купол |
Усечённый куб Четырёхскатный купол | |
Наращённые усечённые додекаэдры[править | править код]
| Полуправильный | J68(М6+М12) | J69(М6+М12+М6) | J70(М12+2М6) | J71(М12+3М6) |
|---|---|---|---|---|
| Усечённый додекаэдр | Наращённый усечённый додекаэдр | Дважды противоположно наращённый усечённый додекаэдр | Дважды косо наращённый усечённый додекаэдр | Трижды наращённый усечённый додекаэдр |

|

|

|

|

|

|

|

|

|

|
Скрученные ромбоикосододекаэдры[править | править код]
| J72(М6+М14+М6=М6+М13+2М6) | J73(М6+М14+М6) | J74(2М6+М13+М6) | J75(3М6+М13) |
|---|---|---|---|
| Скрученный ромбоикосододекаэдр | Дважды противоположно скрученный ромбоикосододекаэдр | Дважды косо скрученный ромбоикосододекаэдр | Трижды скрученный ромбоикосододекаэдр |

|

|

|

|

|

|

|

|
Отсечённые ромбоикосододекаэдры[править | править код]
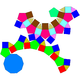
| J76(М6+М14=2М6+М13) | J77(М14+М6) | J78(М13+М6+М6) | J79(М13+2М6) |
|---|---|---|---|
| Отсечённый ромбоикосододекаэдр | Противоположно скрученный отсечённый ромбоикосододекаэдр | Косо скрученный отсечённый ромбоикосододекаэдр | Дважды косо скрученный отсечённый ромбоикосододекаэдр |

|

|

|

|
|

|

|

|
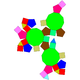
| J80(М14) | J81(М13+М6) | J82(М14+М6) | J83(М13) |
| Дважды противоположно отсечённый ромбоикосододекаэдр | Дважды косо отсечённый ромбоикосододекаэдр | Скрученный дважды отсечённый ромбоикосододекаэдр | Трижды отсечённый ромбоикосододекаэдр |

|

|

|

|

|

|

|
|
Плосконосые антипризмы[править | править код]
Плосконосые[англ.] антипризмы можно построить альтерованием усечённых антипризм. Два тела являются многогранниками Джонсона, одно тело правильное, а остальные нельзя построить с помощью правильных треугольников.
| J84(М25) | Правильный | J85(М28) | Неправильный |
|---|---|---|---|
| Тело Джонсона | Правильный | Тело Джонсона | Вогнутый |
 Плосконосый двуклиноид ss{2,4} |
 икосаэдр ss{2,6} |
 Плосконосая квадратная антипризма ss{2,8} |
 ss{2,10} |

|

|

|
невозможно построить из правильных треугольников |
Другие[править | править код]
| J86(М22) | J87(М22+М3) | J88(М23) | |
|---|---|---|---|
| Клинокорона | Наращённая клинокорона | Большая клинокорона | |

|

|

| |

|

|

| |
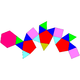
| J89(М21) | J90(М24) | J91(М8) | J92(М20) |
| Уплощённая большая клинокорона | Опоясанный двуклинник | Двойная серпоротонда | Уплощённая треугольная клиноротонда |

|

|

|

|

|

|

|
|
Классификация по типам граней[править | править код]
Треугольные грани[править | править код]
Пять многогранников Джонсона являются дельтаэдрами, то есть все их грани — правильные треугольники:
|
|
Треугольные и квадратные грани[править | править код]
Двадцать четыре многогранника Джонсона имеют только треугольные и четырёхугольные грани:
Треугольные и пятиугольные грани[править | править код]
Одиннадцать тел Джонсона имеют только треугольные и пятиугольные грани:
|
|
Треугольные, квадратные и шестиугольные грани[править | править код]
Восемь многогранников Джонсона имеют только треугольные, квадратные и шестиугольные грани:
|
|
Треугольные, квадратные и восьмиугольные грани[править | править код]
Пять многогранников Джонсона имеют только треугольные, квадратные и восьмиугольные грани:
|
|
Вписываемые в сферу многогранники Джонсона[править | править код]
25 многогранников Джонсона имеют вершины, которые лежат на одной сфере: 1—6, 11, 19, 27, 34, 37, 62, 63, 72—83. Все эти многогранники можно получить из правильных или однородных многогранников путём поворота (купола) или отсечения (купола или пирамиды)[4].
| Октаэдр | Кубооктаэдр | Ромбокубооктаэдр | |||
|---|---|---|---|---|---|
| J1(М2) |
J3(М4)
|
J27(2М4)
|
J4(М5)
|
J19(М5+П8)
|
J37(М5+П8+М5)
|
| Икосаэдр | Икосододекаэдр | ||||
|---|---|---|---|---|---|
| J2(М3) |
J63(М7)
|
J62(М7+М3)
|
J11(М3+А5)
|
J6(М9)
|
J34(2М9)
|
J5(М6)
|
J76(М6+М14)
|
J80(М14)
|
J81(М13+М6)
|
J83(М13)
|
J72(М6+М14+М6)
|
J73(М6+М14+М6)
|
J74(2М6+М13+М6)
|
J75(3М6+М13)
|
J77(М14+М6)
|
J78(М13+М6+М6)
|
J79(М13+2М6)
|
J82(М14+М6)
|
См. также[править | править код]
Примечания[править | править код]
- ↑ Pseudo Rhombicuboctahedra Архивная копия от 8 декабря 2012 на Wayback Machine.
- ↑ Johnson N. W. Convex polyhedra with regular faces (preliminary report) // Notices Amer. Math. Soc. — 1960. — С. 952.
- ↑ Залгаллер, 1967.
- ↑ Johnson solids et al Архивная копия от 2 мая 2014 на Wayback Machine.
Литература[править | править код]
- Гурин А. М. К истории изучения выпуклых многогранников с правильными гранями // Сиб. электрон. матем. изв. — 2010. — Т. 7. — С. A.5—A.23.
- Norman W. Johnson. Convex Solids with Regular Faces // Canadian Journal of Mathematics. — 1966. — Т. 18. — С. 169—200. — ISSN 0008-414X. — doi:10.4153/cjm-1966-021-8. (Содержит оригинальное перечисление 92 тел и гипотезу, что других нет.)
- Залгаллер В. А. Выпуклые многогранники с правильными гранями. — М.—Л.: Наука, 1967. — Т. 2. — 221 с. — (Зап. научн. сем. ЛОМИ). (Первое доказательство, что существует только 92 тел Джонсона.)
- Anthony Pugh. Глава 3. Дальнейшие выпуклые многогранники // Polyhedra: A visual approach. — California: University of California Press Berkeley, 1976. — ISBN 0-520-03056-7.
- Брёндстед А. Введение в теорию выпуклых многогранников. — М.: Мир, 1988.
- Sylvain Gagnon. «Convex polyhedra with regular faces (недоступная ссылка)», Structural Topology. — 1982. — № 6. — P. 83—95.
- Paper Models of Polyhedra Many links
- Johnson Solids by George W. Hart.
- Images of all 92 solids, categorized, on one page
- Weisstein, Eric W. Johnson Solid (англ.) на сайте Wolfram MathWorld.
- VRML models of Johnson Solids by Jim McNeill
- VRML models of Johnson Solids by Vladimir Bulatov
- CRF polychora discovery project attempts to discover CRF polychora, a generalization of the Johnson solids to 4 dimensional space
Ссылки[править | править код]
- Sylvain Gagnon. «Convex polyhedra with regular faces (недоступная ссылка)». — Structural Topology. — 1982. — № 6. — P. 83—95.
- Paper Models of Polyhedra Many links
- Johnson Solids by George W. Hart.
- Images of all 92 solids, categorized, on one page
- Weisstein, Eric W. Johnson Solid (англ.) на сайте Wolfram MathWorld.
- VRML models of Johnson Solids by Jim McNeill
- VRML models of Johnson Solids by Vladimir Bulatov
- CRF polychora discovery project attempts to discover CRF polychora, a generalization of the Johnson solids to 4-dimensional space
Для улучшения этой статьи желательно:
|