Квадратная пирамида

Квадратная пирамида
Тип	Многогранник Джонсона J1
Свойства	выпукла Группа вращений=    C4, [4]+, (44)
Комбинаторика
Элементы	8 рёбер 5 вершин
Грани	4 треугольников 1 квадратов
Конфигурация вершины	4 вида (32.4) 1 вида (34)
Двойственный многогранник	самодвойственна
Развёртка
Классификация
Символ Шлефли	( ) ∨ {4}
Группа симметрии	C4v, [4], (*44)
Медиафайлы на Викискладе

Квадратная пирамида

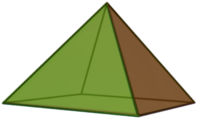
Квадратная пирамида — пирамида, имеющая квадратное основание. Если вершина пирамиды находится на перпендикуляре от центра квадрата, пирамида имеет симметрию C_4v.

Многогранник Джонсона (J₁)

Если все боковые грани пирамиды — правильные треугольники, пирамида является одним из тел Джонсона (J₁).

Тела Джонсона — это 92 строго выпуклых многогранника, имеющие правильные грани, но не являющиеся однородными (то есть не являются ни платоновыми телами (правильными многогранниками), ни архимедовыми, ни призмами, ни антипризмами).

В 1966 Норман Джонсон опубликовал список, в котором присутствовали все 92 тела, и дал им названия и номера. Он не доказал, что их только 92, но высказал гипотезу, что других нет. Виктор Залгаллер в 1969 году доказал, что список Джонсона полон. Квадратная пирамида Джонсона может быть описана единственным параметром — длиной ребра a. Высота H (от середины квадрата до вершины пирамиды), площадь поверхности A (включая все пять граней) и объём V такой пирамиды равны:

$H={\frac {1}{\sqrt {2}}}a$

$A=(1+{\sqrt {3}})a^{2}$

$V={\frac {\sqrt {2}}{6}}a^{3}.$

Другие квадратные пирамиды

Другие квадратные (правильные) пирамиды имеют в качестве сторон равнобедренные треугольники.

Для таких пирамид, имеющих длину основания l и высоту h, площадь поверхности и объём вычисляются по формулам:

$A=l^{2}+l{\sqrt {l^{2}+(2h)^{2}}}$

$V={\frac {1}{3}}l^{2}h.$

Связанные многогранники и соты

Правильные пирамиды

Треугольная	Квадратная	Пятиугольная	Шестиугольная	Семиугольная	Восьмиугольная	Девятиугольная...
Правильная	Равносторонние		Равнобедренные

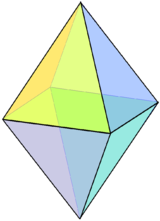
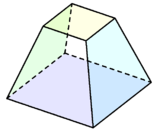
Правильный октаэдр можно считать квадратной бипирамидой, то есть две квадратные пирамиды, соединённые основаниями.	Тетракисгексаэдр можно получить из куба путём наращения коротких квадратных пирамид в каждой грани.	Квадратная усечённая пирамида.

Квадратная пирамида заполняет пространство (образует соты) с тетраэдром, усечённым кубом или кубооктаэдром

Двойственный многогранник

Квадратная пирамида топологически является самодвойственным многогранником. Длины рёбер двойственной пирамиды отличаются из-за полярного преобразования.

Двойственная квадратная пирамида	Развёртка двойственного многогранника

Топология

Квадратную пирамиду можно представить графом «Колесо» W₅.

Литература

• Norman W. Johnson Convex Solids with Regular Faces // Canadian Journal of Mathematics. — 1966. — Т. 18. — С. 169–200. — ISSN 0008-414X. — doi:10.4153/cjm-1966-021-8. Содержит оригинальное перечисление 92 тел и гипотезу, что других нет.

Ссылки

• Virtual Reality Polyhedra Архивная копия от 23 февраля 2008 на Wayback Machine www.georgehart.com: The Encyclopedia of Polyhedra (VRML model Архивная копия от 18 февраля 2012 на Wayback Machine)
• Weisstein, Eric W. Wheel graph (англ.) на сайте Wolfram MathWorld.
• Square Pyramid — Interactive Polyhedron Model
• Virtual Reality Polyhedra Архивная копия от 23 февраля 2008 на Wayback Machine www.georgehart.com: The Encyclopedia of Polyhedra (VRML model Архивная копия от 18 февраля 2012 на Wayback Machine)