Теорема Тейлора
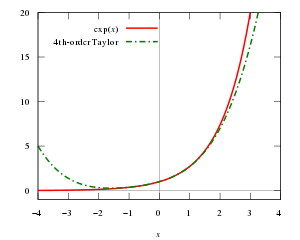
- Эта статья о многочленах Тейлора дифференцируемых функций. О рядах Тейлора аналитических функций см. соответствующую статью.
Теорема Тейлора даёт приближение к функции, дифференцируемой k раз, вблизи данной точки с помощью многочлена Тейлора k-го порядка. Для аналитических функций многочлен Тейлора в данной точке является частичной суммой их ряда Тейлора, который, в свою очередь, полностью определяет функцию в некоторой окрестности точки. Точное содержание теоремы Тейлора до настоящего времени не согласовано. Конечно, существует несколько версий теоремы, применимых в различных ситуациях, и некоторые из этих версий содержат оценки ошибки, возникающей при приближении функции с помощью многочлена Тейлора.
Эта теорема названа в честь математика Брука Тейлора, который сформулировал одну из её версий в 1712 году. Явное выражение для ошибки приближения было дано намного позже Жозефом Лагранжем. Ранее, в 1671 году, Джеймсом Грегори уже было упомянуто следствие из теоремы.
Теорема Тейлора позволяет овладеть приёмами вычислений начального уровня, и она является одним из центральных элементарных инструментов в математическом анализе. При изучении математики она является начальной точкой для изучения асимптотического анализа. Теорема также используется в математической физике. Она также обобщается на функции нескольких переменных и векторные функции для любых размерностей и . Это обобщение теоремы Тейлора является базовым для определения так называемых струй, которые появляются в дифференциальной геометрии и в теории дифференциальных уравнений с частными производными.
Предпосылки для введения теоремы[править | править код]

Если вещественно-значимая функция f(х) является дифференцируемой в точке a, то она имеет линейное приближение в точке a. Это означает, что существует функция h1 такая, что
Здесь
это линейное приближение функции f в точке a. График функции y = P1(x) является касательной к графику функции f в точке x = a. Ошибка приближения такова
Заметим, что ошибка приближается к нулю немного быстрее, чем разница x − a приближается к нулю по мере того, как x стремится к a.

Если мы ищем лучшее приближение f, мы можем использовать многочлен второй степени вместо линейной функции. Вместо нахождения производной от f в точке a, мы можем найти две производные, получив таким образом многочлен, который так же как и f возрастает (или убывает), и так же как и f имеет выпуклость (или вогнутость) в точке a. Многочлен второй степени (квадратный многочлен) в этом случае будет выглядеть следующим образом:
Теорема Тейлора позволяет убедиться, что квадратичное приближение является, в достаточно малой окрестности точки a, лучшим приближением, чем линейное. В частности,
Здесь ошибка приближения такова
которая, при ограниченном характере h2, приближается к нулю быстрее, чем приближается к нулю (x − a)2 по мере того, как x стремится к a.

Таким образом, мы будем продолжать получать более хорошие приближения к f, если будем использовать многочлены всё более высокой степени. В общем, ошибка в приближении функции с помощью полиномов порядка k будет приближаться к нулю немного быстрее, чем приближается к нулю (x − a)k по мере того как x стремится к a.
Это следствие имеет асимптотическую природу: оно лишь говорит нам, что ошибка Rk приближения с помощью многочленов Тейлора k-го порядка Pk приближается к нулю быстрее, чем ненулевой многочлен k-го порядка по мере того как x → a. Оно не говорит нам, насколько велика ошибка в любой окрестности центра приближения, но для этого существует формула для остатка (приведена ниже).
Наиболее полные версии теоремы Тейлора как правило приводят к равномерным оценкам ошибки приближения в малой окрестности центра приближения, но эти оценки не являются адекватными для окрестностей, которые слишком велики, даже если функция f является аналитической. В этой ситуации следует выбирать несколько многочленов Тейлора с разными центрами приближения, чтобы иметь надёжное Тейлорово приближение к исходной функции (см. Анимированный рисунок выше). Возможна также ситуация, когда возрастание порядка многочлена не увеличивает качество приближения вообще, даже если функция f дифференцируется бесконечное число раз. Такой пример приведён ниже.
Теорема Тейлора для функций от одной вещественной переменной[править | править код]
Формулировка теоремы[править | править код]
Точная формулировка большинства базовых версий теоремы такова.
Теорема Тейлора[1] Пусть k ≥ 1 является целым, и пусть функция f : R → R является k раз дифференцируемой в точке a ∈ R. Тогда существует функция hk : R → R такая, что
Многочлен, возникающий в теореме Тейлора, является многочленом Тейлора k-го порядка
функции f в точке a.
Теорема Тейлора описывает асимптотическое поведение остаточного члена
который является ошибкой при нахождении приближения функции f с помощью многочленов Тейлора. Используя «O» большое и «o» малое теорему Тейлора можно сформулировать так
Формулы для остатка[править | править код]
Существует несколько точных формул для остаточного члена Rk многочлена Тейлора, наиболее общая из которых следующая.
Остаток в форме среднего значения. Пусть функция f : R → R является k+1 раз дифференцируемой на интервале и непрерывной на отрезке . Тогда
Это остаточный член в форме Лагранжа[2]. При тех же условиях
Эти уточнения теоремы Тейлора обычно выводятся с помощью формулы конечных приращений.
Можно так же найти и другие выражения для остатка. Например, если G(t) является непрерывной на закрытом интервале и дифференцируемой с нестремящейся к нулю производной на открытом интервале между a и x, то
для некоторого числа ξ между a и x. Эта версия охватывает формы Лагранжа и Коши как частные случаи, и выводится с помощью теоремы Коши о среднем значении (расширенной версии теоремы Лагранжа о среднем значении).
Запись формулы для остатка в интегральной форме является более общей, чем предыдущие формулы, и требует понимания интегральной теории Лебега. Однако она сохраняется также для интеграла Римана при условии, что производная порядка (k+1) от f является непрерывной на закрытом интервале [a,x].
Интегральная форма[4] записи формулы для остатка Пусть f(k) является абсолютно непрерывной на закрытом интервале между a и x. Тогда
Вследствие абсолютной непрерывности f(k) на закрытом интервале между a и x, её производная f(k+1) существует как L1-функция, и это следствие может быть получено с помощью формальных вычислений с использованием теоремы Ньютона — Лейбница и интегрирования по частям.
Оценки остатка[править | править код]
На практике часто бывает полезно численно оценить величину остаточного члена приближения Тейлора.
Будем считать, что f является (k+1)-раз непрерывно дифференцируемой на интервале I, содержащем a. Будем считать, что существуют действительные постоянные числа q и Q такие, что
на всём протяжении I. Тогда остаточный член удовлетворяет неравенству[5]
если x > a, и схожая оценка, если x < a. Это простое следствие из формулы остатка в Лагранжевой форме. В частности, если
на интервале I = (a−r,a+r) с некоторым r>0, то
для всех x∈(a−r,a+r). Второе неравенство называется равномерной оценкой, потому что она сохраняет равномерность для всех x на интервале (a−r,a+r).
Пример[править | править код]

Допустим, мы хотим найти приближение функции f(x) = ex на интервале [−1,1] и убедиться, что ошибка не превышает значения 10−5. В этом примере считаем, что нам известны следующие свойства экспоненциальной функции:
Из этих свойств следует, что f(k)(x) = ex для всех k, и в частности, f(k)(0) = 1. Отсюда следует, что многочлен Тейлора k-го порядка функции f в точке 0 и его остаточного члена в форме Лагранжа даётся формулой
где ξ — это некоторое число между 0 и x. Поскольку ex возрастает согласно (*), мы можем использовать ex ≤ 1 для x ∈ [−1, 0], чтобы оценить остаток на подынтервале [−1, 0]. Для нахождения верхней границы значения остатка на интервале [0,1], можем использовать свойство eξ<<ex для 0<ξ<x, чтобы оценить
используя многочлен Тейлора второго порядка. Выражая из этого неравенства ex, приходим к выводу, что
приняв, что числитель принимает максимальное из всех своих возможных значений, а знаменатель принимает минимальное из всех своих возможных значений. Используя эти оценки значений ex, мы видим, что
и требуемая точность определённо достигается в том случае, когда
(где факториал 7!=5 040 и 8!=40 320.) В конечном счёте, теорема Тейлора приводит к приближению
Отметим, что это приближение позволяет вычислить значение e≈2.71828 с точностью до пятого знака после запятой.
Аналитичность[править | править код]
Разложение Тейлора для вещественных аналитических функций[править | править код]
Пусть является открытым интервалом. По определению, функция является вещественной аналитической, если она на данном участке определена сходимостью степенного ряда. Это означает, что для каждого существует некоторое r > 0 и последовательность коэффициентов ck ∈ R такая, что (a − r, a + r) ⊂ I и
В общем, радиус сходимости степенного ряда может быть вычислен по формуле Коши–Адамара[англ.]
Этот результат основан на сравнении с бесконечно убывающей геометрической прогрессией, и тот же самый метод показывает, что если степенной ряд, разложенный по a, сходится для некоторого b∈R, он должен сходиться равномерно на закрытом интервале [a − rb, a + rb], где rb = |b − a|. Здесь мы только рассмотрели сходимость степенного ряда, и не исключено, что область (a − R,a + R) расширяется за пределы области определения I функции f.
Многочлен Тейлора от вещественной аналитической функции f в точке a
является простым усечением определённого на некотором интервале соответствующего степенного ряда этой функции, и остаточный член на данном интервале даётся аналитической функцией
Здесь функция
также является аналитической, поскольку её степенной ряд имеет тот же радиус сходимости, что и исходный ряд. При условии, что [a − r, a + r] ⊂ I и r < R, все эти ряды сходятся равномерно на интервале (a − r, a + r). Конечно, в случае аналитических функций можно оценить остаточный член Rk(x) путём «обрезания» последовательности производных f′(a) в центре приближения, но при использовании комплексного анализа появляются и другие возможности, которые описаны ниже.
Теорема Тейлора и сходимость ряда Тейлора[править | править код]
Существует разногласие между многочленами Тейлора дифференцируемых функций и рядами Тейлора аналитических функций. Можно рассматривать (справедливо) ряд Тейлора
бесконечное число раз дифференцируемой функции f:R→R как её «многочлен Тейлора бесконечно большого порядка» в точке a. Теперь оценка остатка многочлена Тейлора подразумевает, что для любого порядка k и для любого r>0 существует постоянная Mk,r>0 такая, что
для каждого x∈(a-r, a+r). Иногда эти постоянные могут быть выбраны таким образом, что Mk,r → 0, когда k → ∞ и r остаётся неизменной. Тогда ряд Тейлора функции f сходится равномерно к некоторой аналитической функции
Тут важно упомянуть тонкий момент. Возможна ситуация, когда бесконечное число раз дифференцируемая функция f имеет ряд Тейлора в точке a, который сходится в некоторой открытой окрестности точки a, но предельная функция Tf отличается от f. Важным примером этого феномена является такой
Используя цепное правило можно показать индуктивно, что для любого порядка k,
для некоторого многочлена pk. Функция стремится к нулю быстрее, чем любой полином, по мере того как x → 0, тогда f является бесконечное число раз дифференцируемой и f(k)(0) = 0 для каждого положительного целого k. Теперь оценки для остатка многочлена Тейлора функции f показывают, что ряд Тейлора сходится равномерно к нулевой функции на всей действительной числовой оси. Не будет ошибки в следующих утверждениях:
- Ряд Тейлора функции f сходится равномерно к нулевой функции Tf(x)=0.
- Нулевая функция является аналитической, и каждый коэффициент её ряда Тейлора равен нулю.
- Функция f является бесконечное число раз дифференцируемой, но не аналитической.
- Для любого k∈N и r>0 существует Mk, r>0 такое, что остаточный член многочлена Тейлора k-го порядка функции f удовлетворяет условию (*).
Теорема Тейлора в комплексном анализе[править | править код]
Теорема Тейлора обобщает функции , которые являются комплексно дифференцируемыми на открытом подмножестве U ⊂ C комплексной плоскости. Однако её полезность снижена другими теоремами комплексного анализа, а именно: более полные версии подобных результатов могут быть выведены для комплексно дифференцируемых функций f : U → C с использованием интегральной формулы Коши как показано ниже.
Пусть r > 0 такое, что замкнутый круг B(z, r) ∪ S(z, r) содержится в U. Тогда интегральная формула Коши с положительной параметризацией γ(t)=reit окружности S(z, r) с t ∈ [0,2π] даёт
Здесь все подынтегральные выражения являются непрерывными на окружности S(z, r), что обосновывает дифференцирование под знаком интеграла[англ.]. В частности, если f является один раз комплексно дифференцируемой на открытом множестве U, то она фактически бесконечное число раз комплексно дифференцируема на U. Имеем оценку Коши[6]
для любого z ∈ U и r > 0 такой, что B(z, r) ∪ S(c, r) ⊂ U. Эти оценки подразумевают, что комплексный ряд Тейлора
функции f сходится равномерно в любом круге B(c, r) ⊂ U с S(c, r) ⊂ U в некоторой функции Tf. Кроме того, используя формулу интегрирования по контуру для производных f(k)(c),
таким образом, любая комплексно дифференцируемая функция f на открытом множестве U ⊂ C является комплексно аналитической. Всё то, что было написано выше для вещественных аналитических функций справедливо также и для комплексных аналитических функций, где открытый интервал I заменён на открытое подмножество U ∈ C и a-центрированные интервалы (a − r, a + r) заменена на c-центрированные круги B(c, r). В частности, разложение Тейлора сохраняется в виде
где остаточный член Rk является комплексно аналитическим. При рассмотрении рядов Тейлора методы комплексного анализа позволяют получить несколько более мощные результаты. Например, используя интегральную формулу для любого положительно ориентированную жорданову кривую γ которая параметризирует границу ∂W ⊂ U области W ⊂ U, можно получить выражение для производных f(j)(c) как показано выше, и слегка изменив расчёты для Tf(z) = f(z), прийти к точной формуле
Важная особенность здесь состоит в том, что качество приближения с помощью многочлена Тейлора в области W ⊂ U является мажорируемым значениями функции f на границе ∂W ⊂ U. Так же, применяя оценки Коши к выражению остатка Ряда, получаем равномерные оценки
Пример[править | править код]
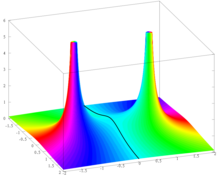
Функция f:R→R, определяемая уравнением
является вещественной аналитической, то есть, в данной области определяется её рядом Тейлора. Один из рисунков, приведённых выше, показывает, что некоторые очень просто задаваемые функции не могут быть выражены с помощью приближения Тейлора в окрестности центра приближения, если эта окрестность слишком велика. Это свойство легко понять в рамках комплексного анализа. Более конкретно, функция f расширяется до мероморфной функции
на компактифицированной комплексной плоскости. Она имеет простые оси в точках z=i и z=−i, и она всюду аналитическая. Её ряд Тейлора, имеющий центром z0, сходится на любом круге B(z0,r) с r<|z-z0|, где тот же ряд Тейлора сходится при z∈C. Вследствие этого ряд Тейлора функции f, имеющий центром точку 0, сходится на B(0,1) и он не сходится для любого z∈C с |z|>1 вследствие имеющихся осей в точках i и −i. По тем же причинам ряд Тейлора функции f, имеющий центром точку 1, сходится на B(1,√2) и не сходится для любого z∈C с |z-1|>√2.
Обобщения теоремы Тейлора[править | править код]
Высшие порядки дифференцируемости[править | править код]
Функция f:Rn → R является дифференцируемой в точке a ∈ Rn тогда и только тогда, когда существует линейная форма L : Rn → R и функция h : Rn → R такая, что
Если этот случай имеет место, то L = df(a) является дифференциалом функции f в точке a. Кроме того, когда частные производные функции f существуют в точке a, то дифференциал f в точке a даётся формулой
Вводя мультииндекс, запишем
для α ∈ Nn и x ∈ Rn. Если все частные производные k-го порядка функции f : Rn → R являются непрерывными в a ∈ Rn, то, по теореме Клеро, можно изменить порядок смешанных производных в точке a, тогда запись
для частных производных высших порядков является правомерной в этой ситуации. То же самое является верным, если все частные производные (k − 1)-го порядка функции f существуют в некоторой окрестности точки a и являются дифференцируемыми в точке a. Тогда можно сказать, что функция f является k раз дифференцируемой в точке a .
Теорема Тейлора для функций многих переменных[править | править код]
Теорема Тейлора для функций многих переменных. Пусть f : Rn → R является k раз дифференцируемой функцией в точке a∈Rn. Тогда существует hα : Rn→R такая, что
Если функция f : Rn → R является k+1 раз непрерывно дифференцируемой в замкнутом шаре B, то можно получить точную формулу для остатка разложения Тейлора до частных производных (k+1)-го порядка от f в этой окрестности. А именно
В этом случае, вследствие непрерывности частных производных (k+1)-го порядка на компактном множестве B, непосредственно получаем
Доказательства[править | править код]
Доказательство теоремы Тейлора для одной вещественной переменной[править | править код]
Пусть[7]
где, как указано в формулировке теоремы Тейлора,
Достаточно показать, что
Доказательство основано на повторяющемся применении правила Лопиталя. Заметим, что каждое j = 0,1,…,k−1, . Отсюда каждая следующая производная числителя функции стремится к нулю в точке , и то же самое справедливо для знаменателя. Тогда
где переход от предпоследнего выражения к последнему следует из определения производной в точке x = a.
Примечания[править | править код]
- ↑ Hazewinkel, Michiel, ed. (2001), "Taylor's formula", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- ↑ Klein, 1998, §20.3; Apostol, 1967, §7.7.
- ↑ Apostol, 1967, §7.7.
- ↑ Apostol, 1967, §7.5.
- ↑ Apostol, 1967, §7.6
- ↑ Rudin, 1987, § 10.26.
- ↑ Stromberg, 1981
Источники[править | править код]
- Apostol, Tom (1967), Calculus, Jon Wiley & Sons, Inc., ISBN 0-471-00005-1.
- Bartle; Sherbert (2000), Introduction to Real Analysis (3rd ed.), John Wiley & Sons, Inc., ISBN 0-471-32148-6.
- Hörmander, L. (1976), Linear Partial Differential Operators, Volume 1, Springer-Verlag, ISBN 978-3540006626.
- Klein, Morris (1998), Calculus: An Intuitive and Physical Approach, Dover, ISBN 0-486-40453-6.
- Pedrick, George (1994), A First Course in Analysis, Springer-Verlag, ISBN 0-387-94108-8.
- Stromberg, Karl (1981), Introduction to classical real analysis, Wadsworth, Inc., ISBN 978-0534980122.
- Rudin, Walter (1987), Real and complex analysis, 3rd ed., McGraw-Hill Book Company, ISBN 0-07-054234-1.
Ссылки[править | править код]
- Taylor Series Approximation to Cosine at cut-the-knot
- Trigonometric Taylor Expansion interactive demonstrative applet
- Taylor Series Revisited at Holistic Numerical Methods Institute














![{\displaystyle [a,x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/692f0edd0d40232c8a69ed5de7b142e1e343eff7)




















































