Дельтоид

Не следует путать с дельтоидой.

На чертеже слева дельтоид выпуклый, справа — невыпуклый.

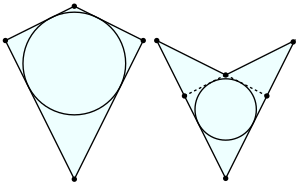
Дельто́ид (от др.-греч. δελτοειδής — «дельтовидный», напоминающий заглавную букву дельта) — четырёхугольник, четыре стороны которого можно сгруппировать в две пары равных смежных сторон.

Свойства

Свойства дельтоида

Вписанная и вневписанная окружности выпуклого дельтоида $ABCD$.

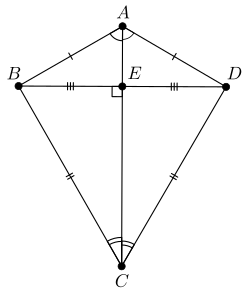
• Диагонали взаимно перпендикулярны.
• В любой выпуклый дельтоид можно вписать окружность
• Точка пересечения диагоналей делит одну из них пополам.
• Другая диагональ является биссектрисой углов.
• Одна диагональ делит дельтоид на два равных треугольника.
• Другая диагональ делит дельтоид на два равнобедренных треугольника, если он выпуклый, и достраивает его равнобедренным треугольником до равнобедренного треугольника, если он невыпуклый.
• Четырёхугольник, вершины которого совпадают с серединами сторон дельтоида, является прямоугольником, стороны которого параллельны диагоналям дельтоида. В частности, если этот прямоугольник — квадрат, то диагонали дельтоида равны, а отрезки, соединяющие середины противоположных сторон перпендикулярны между собой.

Дельтоид, который не является ромбом, обладает также следующими свойствами:

• Противоположные стороны имеют разные длины.
• Углы между сторонами неравной длины равны; другие два противоположных угла не равны.
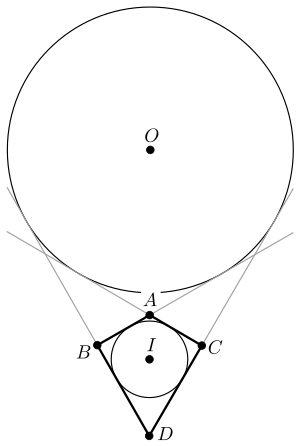
• Если дельтоид выпуклый, то можно построить окружность, касающуюся продолжений всех четырёх сторон (см. рисунок).
• Если дельтоид невыпуклый, то можно построить окружность, касающуюся двух бо́льших сторон и продолжений двух меньших сторон, и окружность, касающуюся двух меньших сторон и продолжений двух бо́льших сторон.

Площадь дельтоида

Здесь приведены формулы, свойственные именно дельтоиду. См. также формулы для площади произвольных четырёхугольников.

$S={\dfrac {d_{1}d_{2}}{2}}$, где $d_{1}$ и $d_{2}$ — длины диагоналей.

$S={ab\sin \alpha }$, где $a$ и $b$ — длины неравных сторон, а $\alpha$ — угол между ними.

$S=\left(a+b\right)r$, где $a$ и $b$ — длины неравных сторон, а $r$ — радиус вписанной окружности.

$S={\dfrac {1}{2}}a^{2}\sin \varphi _{1}+{\dfrac {1}{2}}b^{2}\sin \varphi _{2}$, где $a$ и $b$ — длины неравных сторон, а $\varphi _{1}$ и $\varphi _{2}$ — углы между равными сторонами соответственно.

Частные случаи

• Если угол между неравными сторонами дельтоида прямой, то вокруг него можно описать окружность (вписанный дельтоид).
• Если пара противоположных сторон дельтоида равна, то такой дельтоид является ромбом.
• Если пара противоположных сторон и обе диагонали дельтоида равны, то дельтоид является квадратом. Квадратом является и вписанный дельтоид с равными диагоналями.

Разное

• Дельтоидами являются грани дельтоидального икоситетраэдра, дельтоидального гексеконтаэдра и трапецоэдра.