История математики в Армении
История математики в Армении берёт начало ещё со времён Урартского царства (IX—VII века до н. э.), когда использовались десятичная и шестидесятеричная системы счисления, и роль цифр исполняли клинописи. Сравнение арифметики в древней Армении с урартской указывает на их непосредственную связь. Следы урартской арифметики заметны в древней Армении ещё в эпоху, когда жил и работал Анания Ширакаци, и в арифметике, использовавшейся позже.
Уже после создания армянского письма в самом начале V века, в системе счисления в качестве цифр использовались армянские буквы. Одним из первых армянских учёных в области математики считается крупнейший учёный VII века Анания Ширакаци. Он был автором известного учебника арифметики. Также известны средневековые математики: Лев Математик, Николай Рабдас Артавазд, Ованес Имастасер, Григор Магистрос.
В период XVII—XIX веков, армяне диаспоры открывали армянские школы, в которых велось преподавание в том числе и математики. В этот период активным образом издавались математические книги на армянском языке. В целом, в период XVII—XIX веков, было издано около 90 учебников и пособий армянских авторов.
В XX веке в Ереване были основаны: Ереванский государственный университет (1921), Ереванский политехнический институт (1931, ныне — Национальный политехнический университет Армении), Ереванский педагогический институт (1922, ныне — Армянский государственный педагогический университет имени Хачатура Абовяна), Академия наук Армянской ССР (1943, ныне — Национальная академия наук Республики Армения, в 1944 году основан Институт математики), где ведутся фундаментальные исследования по теории приближений, теории функций, функциональному анализу, интегральному и дифференциальному исчислению и другим областям математики.
Древность и Средневековье[править | править код]
Урарту[править | править код]
Самые древние источники о математических знаниях на территории Армении — это клинописные таблички времён Урартского царства (IX—VII века до н. э.). Они свидетельствуют о том, что в то время использовались десятичная и шестидесятеричная системы счисления[1]. Десятичная система коренным образом отличалась от египетской и была близка к современной системе[2]. Клинописные таблички также свидетельствуют о том, что с помощью нескольких символов записывались достаточно большие целые числа, а также дробные числа, и с ними производились операции сложения и вычитания[1]. Ниже приведены несколько примеров чисел, взятых из царских надписей Сардури II, где единицы — ![]() , десятки —
, десятки — ![]() , сотни —
, сотни — ![]() , тысячи —
, тысячи — ![]() [3]:
[3]:
| 23 — |
Урартийцы, высоко оценивая ассиро-вавилонскую культуру, перенимают у них клинообразные письмена, создают свою письменность и литературу, использованием клинообразных цифр вводят в употребление и делают обиходными крупные числа[4]. Сравнение арифметики в древней Армении с урартской, указывает на их непосредственную связь[4].
Создание армянского алфавита[править | править код]
О математических знаниях армян, особенно в V—VI веках, можно составить представление, с одной стороны, судя по философским и историческим трудам, где исследуются некоторые проблемы математики и астрономии, а с другой стороны, — по остаткам вещественной культуры (замки, палаты, церкви, мосты и оросительные системы), для строительства которых требовались математические знания и точные расчёты, а также по участию армян в международной торговле. В V и в начале VI веков большое количество специально отобранных учеников из Армении были отправлены для продолжения учёбы в Александрию, Афины и в Рим. Об этом свидетельствовали армянские историки V века[5].
До нынешних времён учёным — историкам науки не удалось найти чисто математические тексты, созданные армянами до V века, когда Месропом Маштоцем был создан армянский алфавит[6]. После создания армянского алфавита открылись армянские школы[7], где преподавали также математику. Армянские буквы использовались в качестве цифр, была создана алфавитная десятичная не позиционная система счисления, приведённая ниже (например: Գ — 3, Խ — 40, Չ — 700, Ք — 9000). Между алфавитными системами армян и греков, наряду со сходством, существовало и некоторое различие. Армяне употребляли 36 букв, а греки — 27. Урартская система использовалась параллельно с алфавитной, до тех пор, пока не была окончательно вытеснена последней. Но следы урартской системы остались в новой и передавались из поколения в поколение[8].
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| Единицы | Ա | Բ | Գ | Դ | Ե | Զ | Է | Ը | Թ |
| Десятки | Ժ | Ի | Լ | Խ | Ծ | Կ | Հ | Ձ | Ղ |
| Сотни | Ճ | Մ | Յ | Ն | Շ | Ո | Չ | Պ | Ջ |
| Тысячи | Ռ | Ս | Վ | Տ | Ր | Ց | Ւ | Փ | Ք |
Анания Ширакаци[править | править код]


Дошедшие до нас древние математические труды на армянском языке связаны с именем крупнейшего армянского учёного VII века, основоположника древнеармянского естествознания Анании Ширакаци. То, что до Анании Ширакаци (в V—VI веках) существовали армянские математики и математические труды на армянском языке, очевидно из одного его свидетельства. Во введении к таблицам сложения, Анания Ширакаци упомянул, что он переписывает в кратком виде труды своих предков:
Цель моя, о, любители мудрости и желающие учиться у меня: представить творчество наших предков — искусство осмысления, как живой голос доброго учителя. Учитесь на моих таблицах, хотя и изложил я их кратко, представив немного из многого.
Оригинальный текст (арм.)«Արձանացուցանել ձեզ զջանս նախնեաց զարուեստս համարողութեան: <…> Ուսուցանիջիք իմոցս գծագրեացս թէպէտ և կարճառօտ կարգեցի զսակաւս ի բազմաց…»
Анания Ширакаци внёс большой вклад в математику. Им был составлен учебник арифметики, состоящий из нескольких частей: таблицы с операциями сложения и вычитания, таблицы с операциями умножения и деления, таблицы чисел вида , где пробегает все значения букв армянского алфавита, а частные округляются до целого числа (Шеститысячник, арм. «Վեցհազարյակ»). В Армении также имелись аналогичные таблицы для чисел вида и некоторых других[11]. Задачник, составленный Ширакаци состоит из 24 задач с ответами и из задач с занимательным содержанием (арм. «Խրախճանականներ»). Почти во всех задачах из задачника, отражена жизнь армянского народа: или в условиях говорится о событиях армянской истории, или применяются армянские меры[11]. Задачи — линейные, с одним неизвестным, в одной (№ 22) требуется разделить величину в арифметической прогрессии. Встречающиеся в задачах дроби записаны в виде сумм долей единицы[11].
В начале VII века в Византии, государственной религией которой было христианство, начинается серьёзная борьба против языческой науки и её представителей. В связи с этими событиями, значение естественных наук и математики в Армении сильно падает. Об этом пишет Анания Ширакаци в своей автобиографии[12][13].
Историками науки показано, что начиная с I века до н. э., в Армении применяли следующие меры длины[14]: аспарез (по воздуху), равный шагам, аспарез (по земле) — и шагам, градус, заключающий в себе аспарезов. Миля составляла аспарезов и в одном случае равнялась шагам, в другом — , а шаг — ступням, ступня — пальцам. В VII веке в Армении длину между двумя городами мерили милями, а расстояние между планетой и Землёй — аспарезами[15]. Вся информация о мерах длины была написана в труде Анании Ширакаци «Ашхарацуйц» (арм. Աշխարհացույց)[16].
Математика в Армении после VII века[править | править код]

Продолжателем традиций Ширакаци является известный византийский математик и механик армянского происхождения Лев Математик (ок. 790 — ок. 869). В Константинополе он занимался преподаванием математики, а в 863 году создал и стал первым ректором Константинопольского университета. В математике Лев систематически применял буквы как арифметические символы, тем самым предвосхищая становление алгебры; он значительно упростил сложную символику Диофанта и сделал дальнейший шаг в развитии алгебраического направления в математике[17]. Большой вклад в области математического образования конца XI начала XII века имеет Ованес Имастасер (Любомудрый), известный также как Иоанн Саркаваг (1045/55—1129). Из его математических трудов видно, что в армянских средневековых школах помимо практической, изучали также теоретическую арифметику — теорию чисел. Один из его трудов включает в себя армянскую версию таблиц умножения Пифагора. Его сочинение «Многоугольные числа» опиралось на «Арифметику» Никомаха[11]. Ованес Имастасер является автором труда «Полигональные числа», который использовался в качестве учебника в XI—XII веках[18].
Математическое образование в Армении достигло высокого уровня к XI—XIV веках в армянских средневековых университетах: в Гладзорском университете (основан в 1282 году), в Татевском университете (основан в 1373 году), также в школах Ани, Ахпата и в других учебных заведениях, в том числе и за пределами Армении[1].
Также, продолжателем традиций Ширакаци является византийский математик армянского происхождения XIV века Николай Рабдас Артавазд[19]. Сохранились два его письма на греческом языке. В одном из них говорится о том, как можно представить пальцами руки числа от 1 до 9999, а в другом — об извлечении квадратного корня из чисел[20].
В армянских школах использовались труды греческих классиков. Армянские учёные занимались переводами этих трудов. «Начала» Евклида были переведены на армянский язык несколькими авторами. Сохранившиеся отдельные части перевода относятся и к Анании Ширакаци, и к Григорию Магистросу (перевёл непосредственно с греческого текста в 1051 году)[21][11], и к другим. Согласно Г. Б. Петросяну, старейшим, после арабского, переводом «Начал» Евклида, является армянский перевод Григора Магистроса. Дошедшие до нас фрагменты «Начал» Евклида в армянском переводе содержат перечисление постулатов и аксиом, легших в основу «Начал»; они проливают новый свет в частности на постулат о параллельных[22][23]. В 1959 году был обнаружен ещё один перевод «Начал», сделанный Григором Кесарцем в XVII веке[24].
XVII—XIX века. Армянская математическая литература[править | править код]
В XVII—XVIII веках вопросами математической науки также занимались историки-философы. Больши́е части их изданных трудов были посвящены проблемам арифметики и геометрии[25]. В данный период были изданы многие книги, важные для математики и математического образования.
Первая печатная математическая книга на армянском языке «Искусство счисления» объёмом 147 страниц, была издана неизвестным автором в Марселе в 1675 году. Во введении к этой книге он указал, что написал её для торговцев, поскольку они были неграмотными в математике[26]. Автор не использовал знаки сложения, вычитания, умножения, деления и равенства, хотя соответствующие понятия в книге постоянно использовались. В данном труде были использованы французские, итальянские, иранские математические термины[27]. В дальнейшем, было обнаружено, что «Искусство счисления» является переводом труда Христофора Клавия на латинском языке[28]. В XVII веке также, без указания имени автора и точного времени издания, была издана книга объёмом 120 страниц, 109 из которых — арифметические таблицы: таблица квадратов чисел 1—100, таблица умножения чисел 1—100 на 2, таблица умножения чисел 1—100 на 3 (и так далее до 100), таблица умножения чисел 1—100 на 200, таблица умножения чисел 1—100 на 300 (и так далее до 1000)[27]. В 1781 году в Венеции была издана книга Сукиаса Агмалянца «Арифметика» объёмом 511 страниц[29]. Книга посвящена сложению, вычитанию, умножению, делению, сравнению, арифметическим и геометрическим прогрессиям и логарифмам[30]. В 1794 году также в Венеции была издана книга Саака Проняна «Геометрия» объёмом 423 страницы[31]. Книга посвящена геометрическим теоремам и аксиомам и исследованию геометрических терминов (линии, углы, треугольники, окружности и так далее)[32]. Уже после смерти Саака Проняна в 1810 году в Венеции издаётся его «Тригонометрия». В данной книге впервые в истории армянской математической литературы используются математические знаки[33]. Книга посвящена тригонометрии, решению треугольников, сферической геометрии.
 |
 |
 | ||
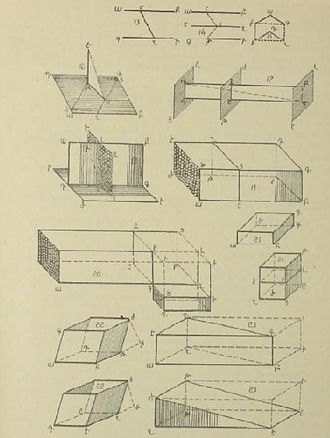
| Титульная страница первой печатной математической книги на армянском языке «Искусство счисления». 1675 год, Марсель | Чертежи из армянской редакции XVII века «Начал» Евклида | |||
В армянской математической литературе XVII—XVIII веков во множестве случаев используются русские термины. Написанные в Астрахани в 1744, 1753 и 1807 годах армянские рукописи, посвящённые вычислительному искусству, содержат арифметические задачи, в которых употребляются термины «рубль», «копейка» и другие, а также русские названия цифр[34]. В то время, в российские учебные заведения Астрахани, в которых преподавали многие предметы, в том числе геометрию, попадали и оканчивали их лишь отдельные представители армянского населения России, количество которых никак не могло удовлетворить фактические потребности в образовании[35]. 12 декабря 1810 года открывается Агабабовская школа в Астрахани, где бо́льшая часть армянского населения имела возможность получить образование[36]. К 1828 году, когда вся Восточная Армения вошла в состав Российской империи, на всей ее территории начали открываться армянские учебные заведения[36]. 9 декабря 1838 года в Константинополе открывается Скютарская семинария[37], преподаватели которой были армянами, получившими европейское образование.
Большое значение имеют труды Гукаса Тертерянца, изданные в Вене. В 1843 году издаются сразу два учебника: «Арифметика» и «Простая Геометрия». В 1846 году издаётся книга «Тригонометрия и конические сечения», объёмом 134 страницы[38]. Вторая часть книги посвящена аналитической геометрии. В конце книги представлены 34 геометрических чертежа.
В целом, в период XVII—XIX веков, было издано около 90 учебников и пособий армянских авторов[39].
XX—XXI века[править | править код]
XX век[править | править код]
В 1921 году в Ереване был основан армянский университет[40]. Преподавание высшей математики начали со дня основания университета на техническом факультете и факультете естествознания, а математиков готовили начиная с 1924 года на физико-математическом отделе педагогического факультета[40]. Но в период 1921—1933 годов, в университете готовили только учителей математики для общеобразовательных и средних профессиональных школ[41]. Уже после 1933 года физико-математический факультет Ереванского государственного университета стал действительно университетским факультетом с 5-летним учебным планом, где стали готовить учёных-математиков[41]. В 1959 году физико-математический факультет был разделён на механико-математический и физический факультеты. С 1963 года на механико-математическом факультете начали готовить учёных в области математической кибернетики, а в 1972 году был создан факультет прикладной математики и информатики[42].
Самостоятельная научно-творческая деятельность в области математики в Советской Армении началась в 1937—1941 годах, когда несколько выпускников физико-математического факультета Ереванского государственного университета продолжили учёбу в Москве и Ленинграде, где защитив диссертации, вернулись в Ереван[43].
-
Здание Президиума Национальной академии наук Республики Армения
10 ноября 1943 года — в самый разгар Великой Отечественной войны, когда постановлением Правительства СССР на базе Армянского филиала Академии Наук СССР была создана Академия Наук Армянской ССР (на основе Армянского филиала Академии наук СССР, созданного в 1935 году, ныне — Национальная академия наук Республики Армения)[44][45]. В 1944 году было создано отделение механики и математики АН Армянской ССР. Позднее, отделение было преобразовано в Институт математики и механики АН Армянской ССР. Институт математики был выделен в отдельную организацию в 1971 году. В 1956 году был создан Ереванский научно-исследовательский институт математических машин (ныне — Ереванский научно-исследовательский институт автоматизированных систем управления). В 1957 году был создан Вычислительный центр АН Армянской ССР (ныне — Институт информатики и проблем автоматизации НАН РА), где начали исследовать математические проблемы кибернетики и вычислительной техники, математическую обеспеченность систем автоматизации, автоматизацию научных исследований. Крупным центром исследований в области прикладной математики, информатики и компьютерных систем также является Национальный политехнический университет Армении. В 1961 году в НПУА был создан факультет компьютерных систем и информатики. Также, в университете есть факультеты прикладной математики и физики, кибернетики[46].

У истоков создания армянской математической школы стоял академик АН Армянской ССР Арташес Шагинян (1906—1978)[47]. Арташес Шагинян был первым советским армянским математиком[48]. После окончания аспирантуры Ленинградского университета в 1937 году он вернулся в Ереван, успешно занимался одновременно научной и педагогической работой[49]. Последователями армянской математической школы стали: М. М. Джрбашян, С. Н. Мергелян, Р. А. Александрян, Н. Х. Арутюнян, Г. Б. Петросян, В. В. Сагателян[арм.], Н. Г. Гаспарян[50], Г. В. Бадалян[51], Н. Е. Товмасян, А. А. Талалян, В. А. Мартиросян, И. Г. Хачатрян[арм.], Г. А. Амбарцумян[арм.]; современные учёные В. С. Захарян, А. Б. Нарсисян, Р. В. Амбарцумян, Н. У. Аракелян, Г. Г. Геворкян, А. А. Саакян и многие другие[52].
Теория приближений[править | править код]
Исследования вопросов о полноте полиномов в комплексной области в Армении были начаты в конце 1930-х годов Арташесем Шагиняном[53] и активным образом продолжались в 1940-х годах им, академиками АН Армянской ССР Мхитаром Джрбашяном (1918—1994) и Сергеем Мергеляном (1928—2008)[54][55]. Была исследована возможность приближения функций полиномами, а также вопросы о наилучшем приближении, относительно интегральной и равномерно-весовой метрик[54]. В случае интегральных метрик, были получены точные признаки для некоторых широких классов областей. Было также получено полное решение равномерно-весового полиномного приближения для действительной оси[54]. Так, со второй половины 1940-х годов, началась организация армянской математической школы теории функций[54].
Сергеем Мергеляном было получено решение для равномерного приближения полиномами в комплексной области[54]. Этот метод был успешно применён также в вопросах о возможности равномерного приближения рациональными функциями, о наилучшем полиномном приближении[54]. Эти работы Сергея Мергеляна были отмечены Сталинской премией.
В 1950-х годах Мхитаром Джрбашяном были начаты исследования среднего, равномерного и касательного приближений целыми функциями, которые получили окончательное решение в 1960—1970-х годах[54]. Полностью были решены задачи о равномерном приближении аналитическими (частично целыми) функциями, и описание скорости касательного приближения[54].
Академиком АН Армянской ССР Норайром Аракеляном были получены решения нескольких общих задач о наилучших приближениях целыми функциями. Эти работы Норайра Аракеляна были отмечены премией Ленинского комсомола[54]. Результаты работ были успешно применены в теории распределения значений[54]. Начиная с 1970-х годов, Мхитаром Джрбашяном и другими были осуществлены исследования полноты и базисности некоторых систем аналитических функций[54]. Норайром Аракеляном были получены ценные результаты о взаимосвязи вопросов о классическом аналитическом продолжении и теории комплексного приближения[54].
Общая теория функций[править | править код]
Серьёзные исследования в области теории функций в Армении начались в 1945 году, когда Мхитаром Джрбашяном была построена теория факторизации неограниченных мероморфных функций в области[54]. В 1950—1960 годах им исследовались вопросы гармонического анализа в комплексной области и теории интегральных преобразований[54]. Джрбашян построил идеальную теорию преобразований вида Фурье — Планшереля для произвольной системы лучей, выходящих из одной точки; получил новые фундаментальные результаты в представлении общих и аналитических функций; расширил и разработал известную классическую теорию Пэли — Винера; вместе с учениками разработал теорию дискретного гармонического анализа в комплексной области[54]. В 1963 году Джрбашяном были определены новые классы мероморфных функций, связанных с функциями на , которые в состоянии включить произвольные мероморфные функции в круге, а также была разработана теория параметрического представления данных функций[54].
Исследования в этой области произвёл и академик НАН РА Ваник Захарян. Мхитаром Джрбашяном и Ваником Захаряном были исследованы граничные свойства подклассов мероморфных функций ограниченного вида[54].
Вопросами дефектных значений общих и мероморфных функций занимался Норайр Аракелян[54]. Впервые использовав методы теории приближений, Норайр Аракелян опровергнул известную гипотезу Рольфа Неванлинны о дефектных значениях целых функций конечного порядка[54].
В геометрической теории мероморфных функций и в теории распределения значений новые результаты получил Григорий Барсегян, разработав теорию Неванлинны — Альфонса[54].
В исследованиях теории аналитических функций важное место занимают вопросы о единственности, в том числе о квазианалитичности[54]. Разрабатывая известные результаты Лоренца Ланделёфа, Арташес Шагинян получил «внутренние» интегральные признаки для аналитических функций в круге, которые в дальнейшем распространил на мероморфные функции в круге[54]. Некоторые из этих результатов Ваник Захарян распространил на классы Джрбашяна[54].
Мхитар Джрбашян, основываясь на своей теории гормонального анализа в комплексной области, обобщил классическую идею о квазианалитичности Данжуа — Карлемана, построив теорию -квазианалитичных классов[54].
Важные исследования в области квазианалитических функций имеет Гайк Бадалян[56]. Бадалян ввёл некоторое обобщение понятия производной и, опираясь на него, построил специальные ряды, более общие, чем тейлоровские[56]. Эти ряды оказались подходящим аналитическим средством для представления функций некоторых квазианалитических классов[56].
Теория функций действительного переменного[править | править код]

Исследования в области функций действительного переменного (аналитических функций) в Армении начались в 1950-х годах[54]. В начальном периоде исследования, в основном, относились к вопросу о представлении измеримых функций ортогональными (в частности — тригонометрическими) рядами и к вопросу о единственности этих рядов[54]. В этой области осуществил исследования академик НАН РА Александр Талалян (1928—2016)[54]. Талалян доказал общие теоремы, согласно которым, рядами полных ортогональных систем могут быть представлены все измеримые функции[54]. С 1965 года под его руководством ведутся исследования общих ортогональных систем и базисов[57]. Получены важные результаты о существовании универсальных (в различных смыслах) ортогональных рядов[57]. Решена задача восстановления рядов Уолша, сходных с интегрируемыми функциями, и доказаны такие теоремы единственности типов Кантора и Валле Пуссена для систем Гаара и Уолша, сходные с которыми, для триганометрических систем не существовали или не были известны до того[57].
Некоторые исследования в области теории функций комплексного переменного произвёл Гайк Бадалян[58]. Задача Сеге о покрытии отрезков была решена Гайком Бадаляном для ограниченных функций из класса [58].
Функциональный анализ[править | править код]

Исследования в области функционального анализа начались в 1950-х годах в Ереванском университете и в Институте математики АН Армянской ССР, и были посвящены вопросу о сходстве граничных задач нового типа в гильбертовом пространстве с задачей Коши[57]. Эти исследования осуществил академик АН Армянской ССР Рафаэль Александрян (1923—1988)[57]. За цикл работ «Математические исследования по качественной теории вращающейся жидкости» он был удостоен Государственной премии СССР. В дальнейшем, несколькими учёными была расширена тематика исследований в областях функционального анализа и интегрального и дифференциального исчислений[57]. Основными направлениями исследований были: теория операторов, операторные уравнения, спектральная теория самосопряжённых операторов[57]. Была разработана идея ядра спектра, в особенности термин резольвенты произвольного самосопряжённого оператора, а также универсальный способ построения полной системы собственных функционалов и теоремы о спектральном анализе по данным функционалам[57]. Были обнаружены асимптотические периодические условия решений нестационарных операторных уравнений некоторых классов, содержащих уравнение Шрёдингера[57].
Впервые на обратные задачи спектрального анализа дифференциальных операторов и на их важность для приложений обратил внимание Виктор Амбарцумян (ему же принадлежит следующий первый результат в этих задачах: если для непрерывной функции краевая задача , где и , имеет спектр , то )[59]. Академик АН СССР Виктор Амазаспович Амбарцумян (1908—1996) является одним из величайших астрофизиков XX века. Немаловажны также его труды по смежным с астрофизикой наукам: по математике и по физике.
Некоторые из результатов о спектре дифференциального оператора в пространстве перенесены академиком АН Армянской ССР, радиофизиком Радиком Мартиросяном на дифференциальные операторы в частных производных[60].
Другие разделы математики[править | править код]
Исследования в области интегрального и дифференциального исчислений начались в Армении в 1930-х годах[57]. В этот период, армянские математики получили некоторые результаты о параболических уравнениях[57]. Обобщённые исследования велись с 1948 года Рафаэлем Александряном[57]. Основными темами исследований были эллиптические, гипоэллиптические, гиперболические, слабые гиперболические, интегральные (в том числе сингулярные интегральные) уравнения[57]. Исследовались граничные задачи нового типа для некоторых неклассических систем дифференциальных уравнений, для уравнения колебания струны в области Дирихле; также было разработано понятие обобщённой собственной функции[57]. Ишханом Саргсяном исследован спектральный анализ задачи Штурма — Лиувилля, а полученные результаты распространены на однородные системы Дирака[57]. Также исследовались обратная задача Штурма — Лиувилля и обратная задача теории рассеяния при наличии уравнений высокого порядка[57].
В областях теории вероятностей и математической статистики исследования в Армении начались в послевоенное время[57]. Был получен ряд результатов по теории случайных процессов, а в дальнейшем — о критерии [57].
В 1970—1980 годах, академиком АН Армянской ССР Рубеном Амбарцумяном было создано новое научное направление — комбинаторная интегральная геометрия[57]. Комбинаторная интегральная геометрия успешно применялась в исследовании решений задач стохастической геометрии, в частности, решены задачи стереологии геометрических случайных процессов[57]. Также, исследовались другие вопросы стохастической геометрии[57].
Исследования в области алгебры начались в 1950-х годах. Исследовались вопросы о представлении квадратных матриц, об анализе некомпактных простых групп Ли, об исследовании тождеств второй степени в универсальных алгебрах и в алгебрах второй степени и другие[61]. Систематическое применение бесконечных систем уравнений к решению конкретных задач математической физики, и в связи с этим, — развитие методов исследования и решения возникающих здесь систем, осуществлены в работах армянских математиков: Б. Л. Абраамяна, Е. А. Александрян, Н. Х. Арутюняна, Н. О. Гулканян, М. М. Джрбащяна, Б. А. Костандяна, Р. С. Минасяна, О. М. Сапонджяна, М. С. Саркисяна, К. С. Чобаняна[62].
XXI век[править | править код]
В начале нового тысячелетия в Армении основные математические исследования ведутся в Институте математики НАН РА и в Ереванском государственном университете. В первые годы работы, Институт математики НАН РА, занимался в основном теорией функций. Со временем, сфера исследований расширилась, и в настоящее время включает комплексный анализ, действительный анализ, дифференциальное и интегральное исчисление, теорию вероятностей, математическую статистику, математическую физику[63].
В Армении издаются следующие математические журналы: «Известия НАН Армении: Математика» (Национальная академия наук Республики Армения, главный редактор — Артур Саакян)[64], Армянский журнал математики (Национальная академия наук Республики Армения, главный редактор — Анри Нерсисян)[65], Математика в высшей школе (Национальный политехнический университет Армении, главный редактор — Ваник Захарян), «Вестник ЕГУ. Серия физики и математики» (Ереванский государственный университет, главный редактор — Варужан Атабекян)[66], также действует Армянский математический союз, который объединяет математиков страны[67].
Примечания[править | править код]
- ↑ 1 2 3 Сагателян, 1981, с. 137.
- ↑ 1 2 Петросян, 1963, с. 93.
- ↑ Петросян, 1963, с. 92.
- ↑ 1 2 Петросян, 1945, с. 71.
- ↑ Петросян, 1966, с. 113.
- ↑ Петросян, 1963, с. 91.
- ↑ Джрбашян, 1987, с. 375.
- ↑ Петросян, 1963, с. 94.
- ↑ Матенадаран имени Маштоца. — № 1770. — С. 385.
- ↑ Петросян, 1963, с. 95.
- ↑ 1 2 3 4 5 Розенфельд и др., 1970, с. 251.
- ↑ Абраамян, 1944.
- ↑ Петросян, 1966, с. 114.
- ↑ Петросян, 1970, с. 227.
- ↑ Петросян, 1972, с. 200.
- ↑ Петросян (ИФЖ), 1979, с. 246.
- ↑ Петросян, 1960, с. 9.
- ↑ Петросян, 1945, с. 40.
- ↑ Кто есть кто, 2005, с. 225.
- ↑ Розенфельд и др., 1970, с. 252.
- ↑ Петросян и др., 1962, с. 148.
- ↑ Петросян, 1945, с. 73.
- ↑ Петросян, 1945, с. 74.
- ↑ Петросян и др., 1962, с. 170.
- ↑ Петросян, 1959, с. 188.
- ↑ Петросян, 1959, с. 191.
- ↑ 1 2 Петросян, 1959, с. 192.
- ↑ Петросян, 1973, с. 40.
- ↑ Петросян, 1959, с. 193.
- ↑ Петросян, 1959, с. 195.
- ↑ Петросян, 1959, с. 196.
- ↑ Петросян, 1959, с. 197.
- ↑ Петросян, 1959, с. 199.
- ↑ Петросян, 1959, с. 187.
- ↑ Хачатурян, 1981, с. 52.
- ↑ 1 2 Петросян, 1979, с. 67.
- ↑ Степанян, 1976, с. 122.
- ↑ Петросян, 1979, с. 68.
- ↑ Сагателян, 1981, с. 134.
- ↑ 1 2 Сагателян, 1964, с. 6.
- ↑ 1 2 Сагателян, 1964, с. 7.
- ↑ Механико-математический факультет (арм.). Ереванский государственный университет. Дата обращения: 5 августа 2014. Архивировано 25 апреля 2019 года.
- ↑ Сагателян, 1964, с. 15.
- ↑ Академия наук Армянской ССР — статья из Большой советской энциклопедии. В. А. Амбарцумян.
- ↑ Об Академии // НАН РА. Архивировано 25 октября 2021 года.
- ↑ Факультеты (арм.). Национальный политехнический университет Армении. Дата обращения: 17 марта 2015. Архивировано из оригинала 27 мая 2015 года.
- ↑ Сагателян, 1964, с. 15—16.
- ↑ Сагателян, 1964, с. 9.
- ↑ Сагателян, 1964, с. 16.
- ↑ Математика в СССР за 40 лет, Том 2, 1959, с. 161.
- ↑ Математика в СССР за 40 лет, Том 2, 1959, с. 50.
- ↑ Армянские математики (англ.). Институт математики НАН Армении. Дата обращения: 18 сентября 2014. Архивировано 3 мая 2019 года.
- ↑ Сагателян, 1964, с. 17.
- ↑ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 Джрбашян, 1987, с. 376.
- ↑ Джрбашян, 1973, с. 22—26.
- ↑ 1 2 3 Математика в СССР за 40 лет, Том 1, 1959, с. 370.
- ↑ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 Джрбашян, 1987, с. 377.
- ↑ 1 2 Математика в СССР за 40 лет, Том 1, 1959, с. 453.
- ↑ Математика в СССР за 40 лет, Том 1, 1959, с. 757.
- ↑ Математика в СССР за 40 лет, Том 1, 1959, с. 771.
- ↑ Джрбашян, 1987, с. 378.
- ↑ Математика в СССР за 40 лет, Том 1, 1959, с. 835.
- ↑ Основные области деятельности (англ.). Институт математики НАН Армении. Дата обращения: 18 сентября 2014. Архивировано 30 апреля 2019 года.
- ↑ Известия НАН Армении: Математика. Дата обращения: 6 августа 2014. Архивировано 19 апреля 2019 года.
- ↑ Армянский журнал математики (англ.). Дата обращения: 6 августа 2014. Архивировано 14 мая 2019 года.
- ↑ Вестник ЕГУ. Серия физики и математики (англ.). Ереванский государственный университет. Дата обращения: 18 сентября 2014. Архивировано 4 мая 2019 года.
- ↑ Армянский математический союз (арм.). Дата обращения: 6 августа 2014. Архивировано 27 сентября 2019 года.
Литература[править | править код]
- Петросян Г. Б. Об армянской географии VII века «Ашхарацуйце» (арм.) = VII հայակական «Աշխարհացոյցի» մասին // Историко-филологический журнал. — 1979. — Թիվ 2. — Էջ 241—246.
- Петросян Г. Б. Вопросы аналитической геометрии в труде Гукаса Тертерянца «Тригонометрия и конические сечения» (арм.) = Անալիտիկ երկրաչափության հարցերը Ղուկաս Տերտերյանցի «Երեքանկիւնաչափութիւն եւ հատածք կոնի» աշխատությունում // История естествознания и техники в Армении. — Ер., 1979. — Թիվ 7. — Էջ 67—90.
- Петросян Г. Б. Первая печатная книга по математике на армянском языке (арм.) = Հայերեն առաջին տպագիր մաթեմատիկական գիրքը // История естествознания и техники в Армении. — Ер., 1973. — Թիվ 5. — Էջ 37—48.
- Петросян Г. Б. К вопросу о трудах «Итинерарий» и «Астрономическая геометрия» (арм.) = «Մղոնաչափք» և «Աստղաբաշխական երկրաչափութիւն» աշխատությունների հարցի շուրջը // Историко-филологический журнал. — 1972. — Թիվ 4. — Էջ 200—208.
- Петросян Г. Б. Меры длины в древнеармянских источниках и их новая интерпретация (арм.) = Երկարության չափերը հին հայկական աղբյուրներում ու դրանց նոր մեկնաբանությունը // Историко-филологический журнал. — 1970. — Թիվ 3. — Էջ 215—228.
- Петросян Г. Б. Математика в Армении в V—VI веках (арм.) = Մաթեմատիկան Հայաստանում V—VI դարերում // Историко-филологический журнал. — 1966. — Թիվ 1. — Էջ 113—124.
- Петросян Г. Б. О некоторых вопросах истории математики в Древней Армении // Вопросы истории физико-математических наук. — М.: Высшая школа, 1963. — С. 91—95. — 524 с. Архивная копия от 8 августа 2014 на Wayback Machine
- Петросян Г. Б., Абраамян А. Г. Новонайденный армянский текст геометрии Евклида (арм.) = Եվկլիդեսի երկրաչափության հայերեն նոր բնագիրը // Историко-филологический журнал. — 1962. — Թիվ 1. — Էջ 148—170.
- Петросян Г. Б. О жизни и деятельности выдающегося ученого-математика IX века Левона (арм.) = IX դարի ականավոր գիտնական-մաթեմատիկոս Լևոնի կյանքի ու գործունեության մասին // История естествознания и техники в Армении. — Ер., 1960. — Թիվ 1. — Էջ 7—20.
- Петросян Г. Б. Армянская математическая литература XVII—XVIII веков (арм.) = Հայկական մաթեմատիկական գրականությունը XVII—XVIII դարերում // Историко-филологический журнал. — 1959. — Թիվ 1. — Էջ 187—201.
- Петросян Г. Б. «Полигональные числа» Ованеса Саркавага (арм.) = Հովհաննես Սարկավագի «Անկիւնաւոր թուեր»-ը // Вестник общественных наук АН Армянской ССР. — 1945. — Թիվ 4. — Էջ 23—42.
- Петросян Г. Б. Армянский древнейший перевод Геометрии Эвклида и его значение для истории математики (арм.) = Էվկլիդեսի երկրաչափության հայերեն հնագույն թարգմանությունը և նրա նշանակությունը մաթեմատիկայի պատմության համար // Вестник общественных наук АН Армянской ССР. — 1945. — Թիվ 1—2. — Էջ 59—76.
- Петросян Г. Б. Арифметика в Урарту по урартским клинописям (арм.) = Թվաբանությունը Ուրարտուում ըստ ուրարտական սեպագիր արձանագրությունների // Вестник общественных наук АН Армянской ССР. — 1945. — Թիվ 3—4. — Էջ 55—72.
- Сагателян В. В. Математика // Армянская советская энциклопедия / В. А. Амбарцумян. — Ер., 1981. — Т. 7. — С. 134—138. — 720 с.
- Сагателян В. В. Развитие математических наук в Советской Армении (арм.) = Մաթեմատիկական գիտությունների զարգացումը Խորհրդային Հայաստանում // История естествознания и техники в Армении. — Ер., 1964. — Թիվ 3. — Էջ 5—38.
- Степанян М. М. Армянские печатные учебники алгебры XIX века (арм.) = Հանրահաշվի հայերեն տպագիր դասագրքերը XIX դարում // История естествознания и техники в Армении. — Ер., 1987. — Թիվ 8. — Էջ 32—42.
- Степанян М. М. Армянские печатные учебники и учебные пособия по арифметике второй половины XIX века (арм.) = XIX դարի երկրորդ կեսի թվաբանության հայերեն տպագիր դասագրքերը և ուսումնական ձեռնարկները // История естествознания и техники в Армении. — Ер., 1979. — Թիվ 7. — Էջ 91—115.
- Степанян М. М. Вариант решения А. Тюляном неопределенных уравнений первой степени (арм.) = Առաջին աստիճանի անորոշ հավասարումների լուծման Հ. Թյուլյանի տարբերակը // История естествознания и техники в Армении. — Ер., 1976. — Թիվ 6. — Էջ 122—133.
- Джрбашян М. М., Сагателян В. В., Талалян А. А., Аракелян Н. У., Александрян Р. А., Нерсисян Г., Амбарцумян Р. В. Математика // Армянская советская энциклопедия / В. А. Амбарцумян. — Ер., 1987. — Т. 13. — С. 375—378. — 688 с.
- Джрбашян М. М. Некоторые основные результаты, полученные армянскими математиками в теории функций за последние 15 лет // История естествознания и техники в Армении. — Ер., 1973. — № 5. — С. 21—36.
- Математика в СССР за сорок лет (1917—1957). — М.: Физматгиз, 1959. — Т. 1. Обзорные статьи. — 1002 с.
- Математика в СССР за сорок лет (1917—1957). — М.: Физматгиз, 1959. — Т. 2. Биобиблиография. — 820 с.
- Розенфельд Б. А., Юшкевич А. П. Математика в Грузии и Армении // История математики. С древнейших времён до начала нового времени / А. П. Юшкевич. — М.: Наука, 1970. — Т. 1. — С. 250—252. — 352 с.
- Никогайос Артавазд // Кто есть кто. Армяне. Биографическая энциклопедия = Ով ով է: Հայեր: Կենսագրական հանրագիտարան. — Ер.: Армянская энциклопедия, 2005. — Т. 2. — С. 225. — 733 с.
- Хачатурян В. Из истории астраханской Агабабовской школы (материальная база школы) (арм.) = Աստրախանի Աղաբաբյան դպրոցի պատմությունից (դպրոցի նյութական բազան) // Вестник общественных наук АН Армянской ССР. — 1981. — Թիվ 1. — Էջ 52—64.
- Абраамян А. Библиография Анании Ширакаци = Անանիա Շիրակացու մատենագրություն. — Ер., 1944.
Эта статья входит в число хороших статей русскоязычного раздела Википедии. |


























