Теорема о сумме углов треугольника
Теорема о сумме углов треугольника — классическая теорема евклидовой геометрии.
Формулировка
[править | править код]Сумма углов любого треугольника на евклидовой плоскости равна 180°.[1]
Доказательство
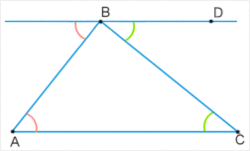
[править | править код]Пусть — произвольный треугольник. Проведём через вершину B прямую, параллельную прямой AC. Отметим на ней точку D так, чтобы точки A и D лежали по разные стороны от прямой BC. Углы DBC и ACB равны как внутренние накрест лежащие, образованные секущей BC с параллельными прямыми AC и BD. Поэтому сумма углов треугольника при вершинах B и С равна углу ABD. Сумма всех трёх углов треугольника равна сумме углов ABD и BAC. Так как эти углы внутренние односторонние для параллельных AC и BD при секущей AB, то их сумма равна 180°. Что и требовалось доказать.
Следствия
[править | править код]- В треугольнике не может быть двух тупых или двух прямых углов, потому что тогда сумма углов была бы больше 180°. По той же причине треугольник не может содержать тупой и прямой углы одновременно.
- У любого треугольника не меньше двух острых углов. Действительно, случай, когда у треугольника только один острый угол или вообще нет острых углов, противоречит предыдущему следствию.
- В прямоугольном треугольнике оба угла при гипотенузе — острые.
- В равнобедренном треугольнике углы при основании равны, поэтому тупым может быть только угол, противолежащий основанию.
- В равнобедренном прямоугольном треугольнике углы при гипотенузе равны (180° — 90°) /2 = 45°.
- В равностороннем треугольнике все три угла совпадают и поэтому равны 180° / 3 = 60°.
- (Теорема о внешнем угле треугольника) Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним[2].
Вариации и обобщения
[править | править код]Многоугольники
[править | править код]Обобщение для симплексов
[править | править код]Существует более сложное соотношение между двугранными углами произвольного симплекса. А именно, если — угол между i и j гранями симплекса, то определитель следующей матрицы (являющейся циркулянтом) равен 0:
- .
Это следует из того, что этот определитель является определителем Грама нормалей к граням симплекса, а определитель Грама линейно зависимых векторов равен 0, и вектор в -мерном пространстве всегда линейно зависимы.
В неевклидовых геометриях
[править | править код]
Приведённое в этой статье доказательство опирается на определённое свойство параллельных прямых, а именно — утверждение о том, что внутренние накрест лежащие углы при параллельных прямых равны. Доказательство этого утверждения, в свою очередь, использует аксиому параллельности евклидовой геометрии. Можно показать, что любое доказательство теоремы о сумме углов треугольника будет использовать аксиому параллельности, и наоборот — из утверждения, что сумма углов треугольника равна 180°, можно вывести аксиому параллельности, если даны остальные аксиомы классической геометрии (абсолютная геометрия)[3].
Таким образом, равенство суммы углов треугольника 180° является одним из основных признаков именно евклидовой геометрии, отличающих её от неевклидовых, в которых аксиома параллельности не выполняется:
- На сфере сумма углов треугольника всегда превышает 180°, разница называется сферическим избытком и пропорциональна площади треугольника. У сферического треугольника могут быть два или даже три прямых или тупых угла.
- Пример. Одна вершина треугольника на сфере — северный полюс. Этот угол может иметь значение до 180°. Две другие вершины лежат на экваторе, соответствующие углы равны 90°.
- В геометрии Лобачевского сумма углов треугольника всегда меньше 180° и может быть сколь угодно малой. Разность также пропорциональна площади треугольника.
Примечания
[править | править код]- ↑ Геометрия по Киселёву Архивная копия от 1 марта 2021 на Wayback Machine, § 81.
- ↑ Элементарная математика, 1976, с. 421.
- ↑ Лелон-Ферран Ж. Основания геометрии. — М.: Мир, 1989. — С. 255—256. — 312 с. — ISBN 5-03-001008-4.
Литература
[править | править код]- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.




