Медиана треугольника

Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок в треугольнике, соединяющий вершину треугольника с серединой стороны, противоположной этой вершине. Иногда медианой называют также прямую, содержащую этот отрезок, а иногда длину этого отрезка. Точка пересечения медианы со стороной треугольника называется основанием медианы.
Если ― треугольник, и , , ― длины сторон (или просто стороны), то медианы, проведённые соответственно из вершин , , к сторонам , , , обычно обозначаются , и .
Связанные определения[править | править код]
Точка пересечения медиан делит каждую медиану на два отрезка. Отрезок от вершины до точки пересечения называется предмедианой, а отрезок от точки пересечения до противоположной стороны постмедианой[1]. В частности можно сказать, что в любом треугольнике отношение предмедианы к постмедиане равно двум.
Свойства[править | править код]
Основное свойство[править | править код]
Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Свойства медиан равнобедренного треугольника[править | править код]
В равнобедренном треугольнике две медианы, проведенные к равным сторонам треугольника, равны, а третья медиана одновременно является биссектрисой и высотой. Верно и обратное: если в треугольнике две медианы равны, то треугольник — равнобедренный, а третья медиана одновременно является биссектрисой и высотой угла при своей вершине.
У равностороннего треугольника все три медианы равны.
Если медианы равнобедренного треугольника, проведённые к боковым сторонам, пересекаются под прямым углом, то косинусы углов при основании этого треугольника равны , а косинус противоположного основанию угла равен .
Свойства оснований медиан[править | править код]

- Теорема Эйлера для окружности девяти точек: основания трёх высот произвольного треугольника, середины трёх его сторон (основания его медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (так называемой окружности девяти точек).
- Отрезок, проведенный через основания двух любых медиан треугольника, является его средней линией. Средняя линия треугольника всегда параллельна той стороне треугольника, с которой она не имеет общих точек.
- Следствие (теорема Фалеса о параллельных отрезках). Средняя линия треугольника равна половине длины той стороны треугольника, которой она параллельна.
- Теркем доказал теорему Теркема[2]. Она утверждает, что если окружность девяти точек пересекает стороны треугольника или их продолжения в 3 парах точек (в 3 основаниях соответственно высот и медиан), являющихся основаниями 3 пар чевиан, то, если 3 чевианы для 3 из этих оснований пересекаются в 1 точке (например 3 медианы пересекаются в 1 точке), то 3 чевианы для 3 других оснований также пересекаются в 1 точке (то есть 3 высоты также обязаны пересечься в 1 точке).
Другие свойства[править | править код]
- Если треугольник разносторонний (неравносторонний), то его биссектриса, проведённая из любой вершины, лежит между медианой и высотой, проведёнными из той же вершины.
- Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
- Медиана делит пополам любой отрезок, параллельный стороне, к которой проведена эта медиана.
- Треугольник делится тремя медианами на шесть равновеликих треугольников. Центры описанных окружностей этих шести треугольников лежат на одной окружности, которая называется окружностью Ламуна.
- Из отрезков, образующих медианы, можно составить треугольник, площадь которого будет равна 3/4 от всего треугольника. Длины медиан удовлетворяют неравенству треугольника.
- В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
- Большей стороне треугольника соответствует меньшая медиана.
- Отрезок прямой, симметричный или изогонально сопряжённый внутренней медиане относительно внутренней биссектрисы, называется симедианой треугольника. Три симедианы проходят через одну точку — точку Лемуана.
- Медиана угла треугольника изотомически сопряжена самой себе.
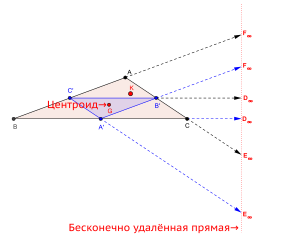
- Трилинейная поляра центроида (точки пересечения трех медиан) — бесконечно удаленная прямая (см. рис.).
Основные соотношения[править | править код]
Чтобы вычислить длину медианы, когда известны длины сторон треугольника, применяется теорема Аполлония (выводится через теорему Стюарта или достроением до параллелограмма и использованием равенства в параллелограмме суммы квадратов сторон и суммы квадратов диагоналей):
- где — медианы к сторонам треугольника соответственно.
В частности, сумма квадратов медиан произвольного треугольника составляет 3/4 от суммы квадратов его сторон:
- .
Обратно, можно выразить длину произвольной стороны треугольника через медианы:
- где — медианы к соответствующим сторонам треугольника, — стороны треугольника.
Площадь любого треугольника, выраженная через длины его медиан:
- где — полусумма длин медиан.
Вариации и обобщение[править | править код]
- Чевиана — отрезок в треугольнике, соединяющий вершину треугольника с точкой на противоположной стороне.
См. также[править | править код]
Примечания[править | править код]
- ↑ Стариков В. Н. 10-е исследование по геометрии (§ До- (пред-)- и пост-чевианы)// Научный рецензируемый электронный журнал МГАУ «Наука и образование». 2020. № 1. 7 с.// http://opusmgau.ru/index.php/see/article/view/ 1604
- ↑ Дмитрий Ефремов. Новая геометрия треугольника Архивная копия от 25 февраля 2020 на Wayback Machine. — Одесса, 1902. — С. 16.
Литература[править | править код]
- Ефремов Дм. Новая геометрия треугольника, 1902 год.




























