Высота треугольника

Высота треугольника — перпендикуляр, опущенный из вершины треугольника на прямую содержащую противоположную сторону. В зависимости от типа треугольника высота может содержаться внутри треугольника (для остроугольного треугольника), совпадать с его стороной (являться катетом прямоугольного треугольника) или проходить вне треугольника у тупоугольного треугольника.
![]() Удобно высоты треугольника обозначать следующим образом.
Удобно высоты треугольника обозначать следующим образом.
Если ― треугольник, и , , ― длины сторон (или просто стороны), то , , ― высоты, опущенные соответственно из вершин , , на стороны , , (или их продолжения).
Свойства[править | править код]
Свойства ортоцентра[править | править код]
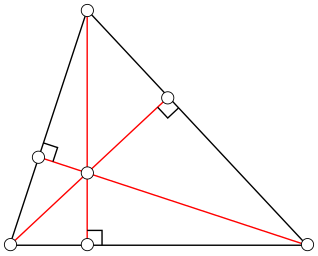
- Все 3 высоты треугольника пересекаются в 1 точке, называемой ортоцентром. Доказательства ниже.
- Ортоцентр изогонально сопряжен центру описанной окружности.
- Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
- Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
- В остроугольном треугольнике ортоцентр лежит внутри треугольника; в тупоугольном — вне треугольника; в прямоугольном — в вершине прямого угла.
Свойства, связанные с описанной окружностью[править | править код]
- Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника. Последний треугольник называют дополнительным треугольником по отношению к первому треугольнику.
- Последнее свойство можно сформулировать так: Центр описанной около треугольника окружности служит ортоцентром дополнительного треугольника.
- Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности.
- Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
- Если О — центр описанной окружности ΔABC, то ,
- , где — радиус описанной окружности; — длины сторон треугольника.
- Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
- Любой отрезок, проведенный из ортоцентра до пересечения с описанной окружностью всегда делится окружностью Эйлера пополам. Ортоцентр есть центр гомотетии этих двух окружностей.
- Теорема Гамильтона. Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих ту же самую окружность Эйлера (окружность девяти точек), что и исходный остроугольный треугольник.
- Следствия теоремы Гамильтона:
- Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника Гамильтона, имеющих равные радиусы описанных окружностей.
- Радиусы описанных окружностей трёх треугольников Гамильтона равны радиусу окружности, описанной около исходного остроугольного треугольника.
Свойства высот равнобедренного треугольника[править | править код]
- Если в треугольнике две высоты равны, то треугольник — равнобедренный, и третья высота одновременно является медианой и биссектрисой того угла, из которого она выходит.
- Верно и обратное: в равнобедренном треугольнике две высоты равны, а третья высота одновременно является медианой и биссектрисой.
Свойства высот равностороннего треугольника[править | править код]
- Теорема Вивиани (Viviani's theorem[англ.]). Для любой точки P внутри равностороннего треугольника сумма перпендикуляров к трем сторонам равна высоте треугольника[1].
Свойства высот равнобедренного треугольника[править | править код]
- Теорема Вивиани обобщенная: для любой точки P на основании равнобедренного треугольника. Сумма расстояний от произвольной точки, лежащей на основании равнобедренного треугольника, до боковых (равных) сторон есть величина постоянная, равная высоте, опущенной на боковую сторону[2].
Свойства высот произвольного треугольника[править | править код]
- Теорема Вивиани обобщенная. Если от концов наименьшей из трех сторон треугольника отложить на двух оставшихся сторонах одинаковые отрезки, равные длине наименьшей из трех сторон, то, соединив два невершинных конца отложенных отрезков прямой, получим геометрическое место точек, лежащих внутри треугольника. Для любой точки P этого геометрического места точек внутри треугольника сумма расстояний до трех сторон есть величина постоянная. [3]
Свойства оснований высот треугольника[править | править код]
- Основания высот образуют так называемый ортотреугольник, обладающий собственными свойствами.
- Описанная около ортотреугольника окружность - окружность Эйлера. На этой окружности также лежат три середины сторон треугольника и три середины трёх отрезков, соединяющих ортоцентр с вершинами треугольника.
- Другая формулировка последнего свойства:
- Теорема Эйлера для окружности девяти точек. Основания трёх высот произвольного треугольника, середины трёх его сторон (основания его внутренних медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (на окружности девяти точек).
- Теорема. В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному.
- Теорема. В треугольнике отрезок, соединяющий основания двух высот треугольника, лежащие на двух сторонах, антипараллелен третьей стороне, с которой он не имеет общих точек. Через два его конца, а также через две вершины третьей упомянутой стороны всегда можно провести окружность.
Свойства середин высот треугольника[править | править код]
- Теорема Шлёмильха. В 1860 году Шлёмильх доказал теорему: три прямые, соединяющие середины сторон треугольника с серединами его соответствующих высот, пересекаются в одной точке. В 1937 году советский математик С. И. Зетель показал, что эта теорема верна не только для высот, но и для любых других чевиан.
- Еще одна очевидная теорема. Середина высоты треугольника всегда лежит на пересекающей ее средней линии треугольника.
- Теорема Ригби. Если к любой стороне остроугольного треугольника провести высоту и касающуюся ее с другой стороны вневписанную окружность, то точка касания последней с этой стороной, середина упомянутой высоты, а также инцентр лежат на одной прямой[4].
- Из теоремы Ригби следует, что 3 отрезка, соединяющих середину каждой из 3 высот треугольника с точкой касания вневписанной окружности, проведенной к той же стороне, что и высота, пересекаются в инцентре.
- Середины X и Y двух высот треугольника ABC, а также середина K стороны BC, из концов которой эти две высоты выходят, а также ортоцентр H лежат на одной окружности, на которой также лежит и пятая точка D — основание третьей высоты AD[5].
- Пусть в треугольнике АВС О — центр описанной окружности. Пусть прямая x проходит через середину высоты треугольника, опущенную из вершины А, и параллельна ОА. Аналогично определяются прямые y и z. Эти 3 прямые пересекаются в одной точке Т, которая является центром окружности Тейлора[6] треугольника АВС[7].
Другие свойства[править | править код]
- Если треугольник разносторонний (неравносторонний), то его внутренняя биссектриса, проведённая из любой вершины, лежит между внутренними медианой и высотой, проведёнными из той же вершины.
- Высота треугольника изогонально сопряжена диаметру (радиусу) описанной окружности, проведенному из той же самой вершины.
- В остроугольном треугольнике две его высоты отсекают от него 2 пары треугольников с 1 общей вершиной, которые подобны.
- В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
- Три части высот данного остроугольного треугольника внутри его ортотреугольника оказываются тремя биссектрисами.
Свойства минимальной из высот[править | править код]
Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:
- Минимальная ортогональная проекция треугольника на прямые, лежащие в плоскости треугольника, имеет длину, равную наименьшей из его высот.
- Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.
- При непрерывном движении двух точек по периметру треугольника друг навстречу другу, максимальное расстояние между ними за время движения от первой встречи до второй, не может быть меньше длины наименьшей из высот треугольника.
- Минимальная высота в треугольнике всегда проходит внутри этого треугольника.
Соотношения[править | править код]
- где — площадь треугольника, — длина стороны треугольника, на которую опущена высота.
- где — произведение боковых сторон, — радиус описанной окружности
- , где — радиус вписанной окружности.
- , где — площадь треугольника.
- , где — сторона треугольника к которой опускается высота .
- Высота равнобедренного треугольника, опущенная на основание:
- где — основание, — боковая сторона.
- — высота в равностороннем треугольнике со стороной .
Теорема о произвольной точке внутри треугольника[править | править код]
Теорема о произвольной точке внутри треугольника. Если pa, pb и pc - расстояния (перпендикулярные отрезки) от любой точки P треугольника до трех его сторон, а ha, hb и hc - длины высот, опущенных на соответствующие стороны (a, b и c), тогда [8]
Следствие теоремы. Если точка P есть инцентр данного треугольника, то pa = pb = pc = . Тогда из последней теоремы имеем:
- , где — радиус вписанной окружности.
Теорема о трех произвольных чевианах внутри треугольника, одна из которых является высотой[править | править код]
Теорема. Если две произвольные чевианы (не обязательно две высоты) внутри остроугольного треугольника пересекаются в точке третьей чевианы, являющейся высотой этого треугольника, тогда сама высота является биссектрисой угла, образованного двумя отрезками прямых, проведенных из основания указанной высоты до двух оснований указанных чевиан (до двух точек пересечения двух указанных чевиан со сторонами). [9]
Теорема о произвольной точке высоты[править | править код]
Теорема о произвольной точке высоты. Если E - произвольная точка на высоте AD любого треугольника ABC, то [10]:77–78
Теоремы о высотах прямоугольного треугольника[править | править код]
Обратная теорема Пифагора[править | править код]
- В прямоугольном треугольнике 3 высоты ha, hb, и hc (первые 2 из которых равны длинам сторон соответственно b и a в этом треугольнике) связаны соотношением, согласно [11][12]
Это соотношение известно под названием обратной теоремы Пифагора (inverse Pythagorean theorem[англ.]).
Теорема о высоте прямоугольного треугольника[править | править код]
Если высота в прямоугольном треугольнике длиной , проведённая из вершины прямого угла, делит гипотенузу длиной на отрезки и , соответствующие катетам и , то верны следующие равенства:
- ;
- (следственно, )
Теорема о проекциях[править | править код]
См. с. 51, ф. (1.11-4)[13]. Теорема о проекциях: . Из теоремы о проекциях следует то, что высота, опущенная, например, из вершины , делит противоположную ей сторону на две части и , считая от вершины к .
История[править | править код]
- Утверждение: «Все 3 высоты треугольника пересекаются в одной точке», называемой теперь ортоцентром, в «Началах» Евклида отсутствует. Часть историков приписывает это утверждение Архимеду и называют его теоремой Архимеда[14]. Ортоцентр впервые в греческой математике использован в «Книге лемм» Архимеда, хотя явного доказательства существования ортоцентра Архимед не привёл.
- В косвенной форме и в явном виде это утверждение («Все 3 высоты треугольника пересекаются в одной точке») встречается у Прокла (410-485) - комментатора Евклида[15].
- Тем не менее до середины девятнадцатого века, ортоцентр нередко называли архимедовой точкой[16].
- Другие историки математики считают автором первого доказательства Уильяма Чеппла (William Chapple (surveyor)[англ.]) (Miscellanea Curiosa Mathematica, 1749 год)[17].
- Сам термин ортоцентр впервые был использован У. Х. Безантом (W. H. Besant[англ.]) в работе "Конические сечения, исследованные геометрически (1869)" ([18]) [19].
Две составные части высоты: предвысота и поствысота [20][править | править код]

- На рис. справа в треугольнике ABC через точку O проведены 3 высоты: AD, BE и CF. Тогда точка O пересечения 3 высот разбивает каждую высоту на 2 отрезка прямых, один из них (который начинается в вершине, а заканчивается в точке пересечения O) мы назовем довысотой или предвысотой, а второй из них (который начинается в точке пересечения O, а заканчивается в точке его пересечения со стороной, противоположной вершине) мы назовем поствысотой.
- Эти 2 термина введены по аналогии с операторами цикла с учетом их изображения на блок-схемах в информатике. Там есть понятия цикла соответственно с пред- и пост-условием в зависимости от того, стоит ли это условие перед или после тела цикла. У нас в роли тела цикла выступает точка O пересечения высот, а в роли условия – первый или второй конец отрезка, вводимого, как понятие для одной из двух частей высоты.
- С помощью этих 2 понятий совсем просто формулируются некоторые теоремы геометрии.
Например, в любом треугольнике (в остро-, прямо-, и в тупоугольном) 3 произведения пред- и поствысоты совпадают [21]. Для остро-и прямоугольного треугольников это утверждение легко доказываемое. Оно верно и для любого тупоугольного треугольника, что удивительно, поскольку в таком треугольнике 2 из 3 высот даже не лежат внутри самого треугольника.
- Замечание. На этом рис. справа в треугольнике ABC чевианы не являются высотами. На следующем рис. справа в треугольнике ABC три высоты:

Вариации по теме. Высоты в четырёхугольнике[править | править код]
Теорема[22]. Пусть — вписанный четырёхугольник, — основание перпендикуляра (высоты), опущенного из вершины на диагональ ; аналогично определяются точки . Тогда точки лежат на одной окружности.
Это утверждение — следствие леммы о шестой окружности.
Примечания[править | править код]
- ↑ Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.: Учпедгиз, 1962. С. 139, п. 128, Следствие
- ↑ Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.:Учпедгиз, 1962. С. 138, п. 127
- ↑ Зетель С. И. Новая геометрия треугольника. Пособие для учителей. 2-е издание. М.:Учпедгиз, 1962. С. 137, п. 126. Задача, черт. 106
- ↑ Ross Honsberger. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: The Mathematical Association of America, 1996, ISBN 978-0883856390. p. 30, Figure 34, §3. An Unlikely Collinearity.
- ↑ Ross Honsberger. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: The Mathematical Association of America, 1996, ISBN 978-0883856390. p. 33, figure 40, §Exercise 3.2
- ↑ Круг Тейлора// https://deru.abcdef.wiki/wiki/Taylor-Kreis
- ↑ Мякишев А. Прогулки по окружностям: от Эйлера до Тейлора// Математика. Все для учителя! № 6 (6). июнь 2011. с. 3, задача 2, рис. 3// https://www.geometry.ru/persons/myakishev/papers/circles.pdf Архивная копия от 22 августа 2022 на Wayback Machine
- ↑ Johnson, 2007, p. 74, Section 103c
- ↑ Зетель С. И. Новая геометрия треугольника. 2-е изд. М.: Учпедгиз, 1962. с. 85, п. 70. черт. 62
- ↑ Posamentier A. S., Salkind. C.T.Challenging Problems in Geometry, Dover Publishing Co., second revised edition, 1996.
- ↑ Voles, Roger, "Integer solutions of ," Mathematical Gazette 83, July 1999, 269–271.
- ↑ Richinick, Jennifer, "The upside-down Pythagorean Theorem," Mathematical Gazette 92, July 2008, 313–317.
- ↑ Корн Г.А., Корн Т.М. Справочник по математике для научных работников и инженеров. — М.: «Наука», 1974. — 832 с. Архивировано 19 января 2015 года.
- ↑ Ефремов Д. Новая геометрия треугольника. Одесса, 1902. С. 9, п. 16. Высоты треугольника. Теорема Архимеда.
- ↑ Nathan Altshiller-Court. "College Geometry. An Introduction to the Modern Geometry of the Triangle and the Circle". Second Edition. Mineola, New York: Dover Publications, Inc. 2007. P. 298, §175.
- ↑ Maureen T. Carroll, Elyn Rykken. Geometry: The Line and the Circle. Дата обращения: 10 апреля 2020.
- ↑ Bogomolny, Alexander, "A Possibly First Proof of the Concurrence of Altitudes", Cut The Knot, Архивировано 7 мая 2021, Дата обращения: 17 ноября 2019 Источник. Дата обращения: 10 апреля 2020. Архивировано 7 мая 2021 года.
- ↑ Conic Sections Treated Geometrically, 1869. Ссылка: 1895: Conic sections treated geometrically Архивная копия от 18 апреля 2018 на Wayback Machine from Cornell University Historical Math Monographs.
- ↑ Nathan Altshiller-Court. "College Geometry. An Introduction to the Modern Geometry of the Triangle and the Circle". Second Edition. Mineola, New York: Dover Publications, Inc. 2007. P. 298, §176
- ↑ Стариков В.Н. 10-е исследование по геометрии (§ До- (пред-)- и пост-чевианы). Научный рецензируемый электронный журнал МГАУ "Наука и образование". 2020. № 1. 7 с.// http://opusmgau.ru/index.php/see/article/view/1604 Архивная копия от 29 июня 2020 на Wayback Machine
- ↑ Nathan Altshiller-Court. "College Geometry. An Introduction to the Modern Geometry of the Triangle and the Circle". Second Edition. Mineola, New York: Dover Publications, Inc. 2007. P. 94, §177. Theorem.
- ↑ Вокруг задачи Архимеда. Упр. 7, рис. 11, следствие, c. 5 Архивная копия от 29 апреля 2016 на Wayback Machine.
Литература[править | править код]
- Johnson, Roger A. Advanced Euclidean Geometry. — Dover, 2007. — ISBN 978-0-486-46237-0.



















































