Диэдрическая группа

Снежинка имеет Dih₆ диэдральную симметрию, ту же самую, что и правильный шестиугольник.

В математике, диэдральной группой (D_n, группа диэдра) называется группа симметрии правильного многоугольника, включающая как вращения, так и осевые симметрии. Диэдральные группы являются простейшими примерами конечных групп, и играют важную роль в теории групп, геометрии, и химии. Хорошо известно и совершенно тривиально проверяется, что группа, образованная двумя инволюциями с конечным числом элементов в области определения является диэдральной группой.

См. также: Диэдральная симметрия в 3-мерном пространстве

Обозначения

Имеется два (основных) вида записи диэдральной группы, связанной с n-сторонним многоугольником. В геометрии группа записывается как D_n, в то время как в алгебре та же самая гуппа обозначается как D_2n, используя в качестве индекса число элементов в группе. Имеется также нотация Коксетера, в которой осевая симметрия обозначается как [n] (порядка 2n), и вращения как [n]⁺ (порядка n). Еще одна запись — нотация орбиобразия, в которой осевая симметрия обозначается как *nn, а вращения — как n.

В этой статье D_n (или, иногда, Dih_n) относится к симметриям правильного n-угольника.

Определение

Элементы

Шесть осевых отражений правильного шестиугольника

Правильный n-угольник имеет 2n различных симметрий: n поворотов и n осевых отражений], образующих диэдральную группу D_n. Если n нечетно, каждая ось симметрии проходит через середину одной из сторон и противоположную вершину. Если n четно, имеется n/2 осей симметрии, соединяющих середины противоположных сторон и n/2 осей, соединяющих противоположные вершины. В любом случае, имеется n осей симметрии и 2n элементов в группе симметрий. Отражение относительно одной оси, а затем относительно другой, приводит к вращению на удвоенный угол между осями. Изображения ниже показывают результат действия элемента D₈ на дорожный знак Стоп:

Первая строка показывает восемь вращений, а вторая — восемь отражений.

Структура группы

Как и для любого другого геометрического объекта, композиция двух симметрий правильного многоугольника снова будет симметрией. Таким образом, симметрии правильного многоугольника образуют конечную группу.

Композиция двух отражений дает вращение.

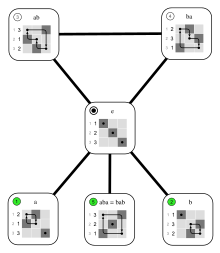
Таблица Кэли показывает эффект композиции в группе D₃ (симметрии правильного треугольника). R₀ обозначает тождественное преобразование, R₁ и R₂ означает вращение против часовой стрелки на 120 и 240 градусов, S₀, S₁, и S₂ означают отражение относительно осей, показанных на рисунке справа.

	R0	R1	R2	S0	S1	S2
R0	R0	R1	R2	S0	S1	S2
R1	R1	R2	R0	S1	S2	S0
R2	R2	R0	R1	S2	S0	S1
S0	S0	S2	S1	R0	R2	R1
S1	S1	S0	S2	R1	R0	R2
S2	S2	S1	S0	R2	R1	R0

Например, S₂S₁ = R₁, поскольку отражение S₁, а затем отражение S₂ дают поворот на 120 градусов. Обратите внимание на то, что композиция не коммутативнна.

В общем случае, группа D_n имеет элементы R₀,…,R_n−1 и S₀,…,S_n−1, и композицию (операцию над элементами), которая задается формулой:

$R_i\,R_j = R_{i+j},\;\;\;\;R_i\,S_j = S_{i+j},\;\;\;\;S_i\,R_j = S_{i-j},\;\;\;\;S_i\,S_j = R_{i-j}.$

Во всех случаях сложение и вычитание индексов должно выполняться с использованием вычетов по модулю n.

Матричное представление

Симметрии пятиугольника являются линейными отображениями.

Если расположить центр правильного многоугольника в начале координат, элементы диэдральной группы работают как линейное отображение плоскости. Это позволяет нам представить элементы D_n как матрицы, с Умножение матриц в качестве операции композиции. Пример 2-мерного представления группы.

В качестве примера, элементы группы D₄ можно представить как 8 следующих матриц:

$\begin{matrix} R_0=\bigl(\begin{smallmatrix}1&0\\[0.2em]0&1\end{smallmatrix}\bigr), & R_1=\bigl(\begin{smallmatrix}0&-1\\[0.2em]1&0\end{smallmatrix}\bigr), & R_2=\bigl(\begin{smallmatrix}-1&0\\[0.2em]0&-1\end{smallmatrix}\bigr), & R_3=\bigl(\begin{smallmatrix}0&1\\[0.2em]-1&0\end{smallmatrix}\bigr), \\[1em] S_0=\bigl(\begin{smallmatrix}1&0\\[0.2em]0&-1\end{smallmatrix}\bigr), & S_1=\bigl(\begin{smallmatrix}0&1\\[0.2em]1&0\end{smallmatrix}\bigr), & S_2=\bigl(\begin{smallmatrix}-1&0\\[0.2em]0&1\end{smallmatrix}\bigr), & S_3=\bigl(\begin{smallmatrix}0&-1\\[0.2em]-1&0\end{smallmatrix}\bigr). \end{matrix}$

В общем случае, матрицы для элементов D_n имеют следующий вид:

$\begin{align} R_k & = \begin{pmatrix} \cos \frac{2\pi k}{n} & -\sin \frac{2\pi k}{n} \\ \sin \frac{2\pi k}{n} & \cos \frac{2\pi k}{n} \end{pmatrix} \ \ \text{and} \\ S_k & = \begin{pmatrix} \cos \frac{2\pi k}{n} & \sin \frac{2\pi k}{n} \\ \sin \frac{2\pi k}{n} & -\cos \frac{2\pi k}{n} \end{pmatrix} . \end{align}$

R_k — это матрица поворота против часовой стрелки на угол 2πk ⁄ n, а S_k — отражение относительно оси, имеющей угол πk ⁄ n к оси X.

Маленькие диэдральные группы

Для n = 1 получим Dih₁. Это обозначение используется редко, разве что для обозначении в последовательности других групп, поскольку группа эквивалентна Z₂.

Для n = 2 получим Dih₂ четверную группа Клейна. Оба случая являются исключениями в серии:

• Они абелевы, для всех остальных n группа Dih_n не абелева.
• Они не являются подгруппами симметрической группы S_n, поскольку 2n > n! для этих n.

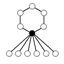
граф циклов диэдральных групп состоит из одного цикла длины n и n циклов длины 2. Темные вершины графа циклов ниже показывают тождественное преобразование, белые — остальные элементы группы. Цикл состоит из последовательных степеней остальных элементов.

Dih1 Dih2 Dih3 Dih4 Dih5 Dih6 Dih7

Dih3 = S3

Dih4

Диэдральная группа как группа симметрии в 2D и группа вращений в 3D

Примером абстрактной группы Dih_n и общепринятого пути графического представленияt является группа D_n изометрий плоскости, не двигающих начало координат. Эти группы формируют одну из двух серий дискретных групп точек на плоскости. D_n состоит из n вращений на угол, кратный 360°/n, вокруг начала координат, и отражений относительно n осей, проходящих через центр координат и углом к остальным осям, кратным 180°/n. Эти точки представляют группу симметрии правильного многоугольника с n сторонами (для n ≥ 3).

Диэдральная группа D_n is порождается вращением r порядка n и отражением s порядка 2, такими что

$srs = r^{-1} \,$

В терминах геометрии: зеркальное отражение вращения выглядит как обратное вращение.

В терминах комплексных чисел: умножением на $e^{2\pi i \over n}$ и сопряжением.

В терминах матриц: задав

$r_1 = \begin{bmatrix}\cos{2\pi \over n} & -\sin{2\pi \over n} \\[8pt] \sin{2\pi \over n} & \cos{2\pi \over n}\end{bmatrix} \qquad s_0 = \begin{bmatrix}1 & 0 \\ 0 & -1\end{bmatrix}$

и определив $r_j = r_1^j$ и $s_j = r_j \, s_0$ для $j \in \{1,\ldots,n-1\}$ мы можем записать правила образования  D_n как

$r_j \, r_k = r_{(j+k) \text{ mod }n}$

$r_j \, s_k = s_{(j+k) \text{ mod }n}$

$s_j \, r_k =s_{(j-k) \text{ mod }n}$

$s_j \, s_k = r_{(j-k) \text{ mod }n}.$

(Сравните Матрица поворота.)

Диэдральная группа D₂ порождается вращением r на 180 градусов, и симметрией s относительно оси X. Элементы D₂ можно представить как {e, r, s, rs}, где e — тожественное преобразование и rs — симметрия относительно оси 'Y.

Четыре элемента D₂ (здесь ось X вертикальна)

D₂ изоморфна четверной группе Клейна.

Для n>2 операции вращения и отражения относительно прямой не коммутативны и D_n не является абелевой. Например, в D₄, вращение 90 градусов, а затем отражение дает совсем другой результат, нежели отражение, а затем вращение.

D₄ не абелево (ось X здесь вертикальна).

Таким образом, наряду с очевидным приложением к проблемам симметрии на плоскости, эти группы служат простейшими примерами неабелевых групп, и часто используются как контрпримеры для теорем, ограниченных абелевыми группами.

2n элементов D_n можно записать как e, r, r², …, rⁿ⁻¹, s, r s, r² s, …, rⁿ⁻¹ s. Первые n перечисленных элементов являются вращениями, остальные n — отражения относительно осей (все они имеют порядок  2). Результатом двух вращений или двух отражений будет вращение Результат вращения и отражения будет отражением.

Таким образом, мы установили, что D_n является подгруппой O(2).

Однако, обозначение D_n используется для подгрупп SO(3), которые тоже являются группами типа Dih_n: группа симметрии многоугольника, вложенного в трехмерное пространство (если n ≥ 3). Такие фигуры можно понимать как вырожденные тела (отсюда и название диэдрон (dihedron').

Примеры симметрии двумерных диэдралов

• 

  2D D₆ – (отвергнутый символ) Красная звезда Давида

• 

  2D D₂₄ – Ашока Чакра - символ на флаге Индии.

Эквивалентные определения

Следующие определения Dih_n эквивалентны:

• Группа автоморфизма графа состоит только из цикла с n вершинами (если n ≥ 3).
• Группа с представлением

$D_{n}=\langle r, s \mid r^n = 1, s^2 = 1, s^{-1}rs = r^{-1} \rangle$

или

$D_n=\langle x, y \mid x^n = y^2 = (xy)^2 = 1 \rangle.$

Из второго представления следует, что Dih_n принадлежит к классу групп Коксетера.

Свойства

Свойства диэдральных групп Dih_n с n ≥ 3 зависят от четности n. Например, центр группы Dih_n состоит только из тождества при нечетном n, и из двух элементов при четном, а именно, из тождества и r^n / 2

Для нечетных n, абстрактная группа Dih_2n изоморфна прямому произведению Dih_n и Z₂.

Если m делит n, то Dih_n имеет n / m подгрупп вида Dih_m, и одну подгруппу Z_m. Таким образом, полное число подгрупп группы Dih_n (n ≥ 1), равно d(n) + σ(n), где d(n) — число делителей n и σ(n) — сумма делителей  n.

Сопряженность классов отражений

Все отражения попарно сопряжены в случае нечетного n, но распадаются на два класса сопряженности при четном n. В терминах изоморфизма правильных n-угольников: для нечетных n любую пару отражений можно представить как вращения, в то время как для четных n только половина отражений может быть получена из некоторого вращения поворотами. С геометрической точки зрения, в нечетном многоугольнике каждая ось симметрии проходит через одну из вершин и середину противоположной стороны, а в четном имеется два набора осей, каждый набор соответствует своему классу сопряженности — оси, проходящие через вершины и оси, проходящие через середины сторон.

Алгебраически, это представители сопряженных элементов из теоремы Силова: для нечетных n любое отражение вместе с тожественным элементом образует подгруппу порядка 2, являющуюся силовской 2-подгруппой ($2=2^1$ — максимальная степень двойки, делящая $2n=2(2k+1)$), в то время как для четных n, эти подгруппы 2-го порядка не являются силовскими, поскольку 4 (наибольшая степень двойки) делит порядок группы.

Для четного n вместо этого имеется внешний автоморфизм, переставляющий два типа отражений

Группы автоморфизмов

Автоморфизм группы Dih_n изоморфен аффинной группе Aff(Z/nZ) $=\{ax + b \mid (a,n) = 1\}$ и имеет порядок $n\phi(n),$, где $\phi$ — функция Эйлера, равная количеству натуральных чисеk, меньших n и взаимно простых с ним.

Это можно понять в терминах генератора отражений и элементарных вращений (вращений на $k(2\pi/n)$, для k взаимно-простого с n). Какой автоморфизм будет внутренним, а какой внешним, зависит от четности n.

• Для нечетного n диэдральная группа не имеет центра, так что любой элемент определяет нетривиальный внутренний автоморфизм. Для четного n вращение на 180° (отражение относительно центра координат) является нетривиальным элементом центра.
• Таким образом, для нечетного n, внутренняя группа автоморфизма имеет порядок 2n, а для четного — порядок n.
• Для нечетного n, все отражения являются сопряженными, для четного, они распадаются на два класса (те, которые проходят через две вершины, и те, которые проходят через середины сторон), и эти два класса связаны с внешним автоморфизмом, который можно представить как вращение на $\pi/n$ (половину угла минимального вращения).
• Вращения дают нормальную подгруппу. Сопряжение отражения меняет знак (направление) вращения, но в остальном их не меняют. Автоморфизм, умножающий углы на k (взамнопростое с n) является внешним, если только не $k=\pm 1.$

Примеры автоморфизма групп

Dih₉ имеет 18 внутренних автоморфизмов. Как группа изометрий двумерного пространства, D₉ имеет отражения с интервалом 20°. 18 внутренних автоморфизмов обеспечивают вращения отражений на число, кратное 20°, и отражения. Как группы изометрии они все являются аутоморфизмами. Имеется еще, вдобавок, 36 внешних автоморфизмов, например, умножая угол вращения на 2.

Обобщения

Имеется несколько важных обобщений диэдральных групп:

• Бесконечная диэдральная группа — это бесконечная группа с алгебраической структурой, похожей на структуру конечных диэдральных групп. Ее можно рассматривать как группу симметрий целых чисел.
• Ортогональная группа O(2), то есть группа симметрии круга, имеет свойства, похожие на свойства конечных диэдральных групп
• Семейство обобщенных диэдральных групп включает вышеприведенные расширения, как и многие другие.
• Квазиэдральные группы — это семейство конечных групп со свойствами, похожими на свойства конечных диэдральных групп.

Смотрите также

• Дициклическая группа
• Массив Костаса

Внешние ссылки

• Dihedral Group n of Order 2n by Shawn Dudzik, Wolfram Demonstrations Project.
• Dihedral group at Groupprops
• Miller W., Symmetry Groups and Their Applications. Academic Press, 1972
• Поклонский Н. А. Точечные группы симметрии: Учеб. Пособие — Мн.: БГУ, 2003. ISBN 985-445-965-9
• Аминов ЛюК. Теория симметрии (конспекты лекций и задачи). ЬюЖ Мн-т компьютерных исследований, 2002. — 192с.
• Вейль Г. Симметрия. — М.: Наука, 1968. — 152с.
• Вигнер Е. Этюды о симметрии. — М.: Мир, 1971. −320с.
• Голод П. И., Климык А. У. Математические основ теории симметрий. — М.: РХД, 2001. — 528с.
• Узоры симметрии, Под ред. М. Сенешаль, Дж. Флека. — Ь.: Мир, 1980. — 271с.
• Смирнов Е. Ю. Группы отражений и правильные многогранники. --М.: МЦНМО, 2009. — 48 с. ISBN 978-5-94057-525-2
• Фларри Р., Группы симметрии. Теория и химические приложения. М., Мир, 1983