Квадратичная функция одной переменной

Квадратичная функция — целая рациональная функция второй степени вида , где и . Таким образом, если переменная и некоторый квадратный трёхчлен связаны функциональной зависимостью ( рассматривается как независимая переменная величина, сам трёхчлен — как зависимая), то её такую функцию называют квадратичной. Графиком квадратичной функции является парабола. Многие свойства графика квадратичной функции так или иначе связаны с вершиной параболы, которая определяет положение и внешний вид графика функции.
Обзор основных свойств[править | править код]
Многие свойства квадратичной функции зависят от значения коэффициента . В следующей таблице приводится обзор основных свойств квадратичной функции[1]. Их доказательство рассматривается в статье в соответствующих разделах.
| Свойство | ||
|---|---|---|
| Область определения функции | ||
| Множество значений функции | ||
| Чётность функции | Чётная функция при ; ни чётная, ни нечётная при | |
| Периодичность функции | Непериодическая функция | |
| Непрерывность функции | Всюду непрерывная функция, точек разрыва нет | |
| Нули функции | , если нет действительных нулей, если | |
| Предел функции при | при | при |
| Дифференцируемость функции | Всюду многократно дифференцируема: | |
| Точки экстремума (абсолютный экстремум) | (минимум) | (максимум) |
| Интервалы строгой монотонности | убывает на возрастает на |
возрастает на убывает на |
| Выпуклость функции | Всюду выпуклая вниз функция | Всюду выпуклая вверх функция |
| Точки перегиба | Точки перегиба отсутствуют | |
| Ограниченность функции | Ограничена снизу | Ограничена сверху |
| Наибольшее значение функции | Отсутствует (неограничена сверху) | |
| Наименьшее значение функции | Отсутствует (неограничена снизу) | |
| Положительные значения функции | ||
| Отрицательные значения функции | ||
Влияние коэффициентов на трансформацию графика[править | править код]
Стандартная запись уравнения квадратичной функции[править | править код]
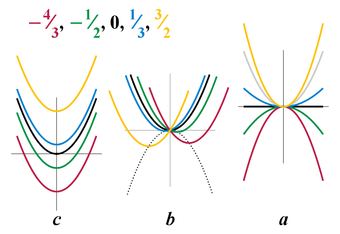
Действительные числа , и в общей записи квадратичной функции называются её коэффициентами. При этом коэффициент принято называть старшим, а коэффициент — свободным. Изменение каждого из коэффициентов приводит к определённым трансформациям параболы.
По значению коэффициента можно судить о том, в какую сторону направлены её ветви (вверх или вниз) и оценить степень её растяжения или сжатия относительно оси ординат:
- Если , то ветви параболы направлены вверх, то есть её вершина расположена снизу.
- Если , то ветви параболы направлены вниз, то есть её вершина расположена сверху.
- Если , то парабола сжата по оси ординат, то есть кажется более широкой и плоской.
- Если , то парабола растянута по оси ординат, то есть кажется более узкой и крутой.
Влияние значения коэффициента наиболее просто позволяет проиллюстрировать квадратичная функция вида , то есть в случае и . В случае квадратичная функция превращается в линейную.
Изменение коэффициента повлечёт за собой сдвиг параболы как относительно оси абсцисс, так и относительно оси ординат. При увеличении значения на 1 произойдёт сдвиг параболы на влево и одновременно на вниз. При уменьшении на 1 произойдёт сдвиг параболы на вправо и одновременно на вверх. Такие трансформации объясняются тем, что коэффициент характеризует угловой коэффициент касательной к параболе в точке пересечения с осью ординат (то есть при ).
Коэффициент характеризует параллельный перенос параболы относительно оси ординат (то есть вверх или вниз). При увеличении значения этого коэффициента на 1, парабола переместится на 1 вверх. Соответственно, если уменьшить коэффициент на 1, то и парабола сместится на 1 вниз. Так как коэффициент также влияет на положение вершины параболы, то по одному лишь значению коэффициента нельзя судить о том, расположена ли вершина выше оси абсцисс или ниже неё.
Запись квадратичной функции через координаты вершины параболы[править | править код]
Любая квадратичная функция может быть получена с помощью растяжения/сжатия и параллельного переноса простейшей квадратичной функции . Так, график функции вида получается путём сжатия (при ) или растяжения (при ) графика функции в раз с последующем его параллельным переносом на единиц вправо и единиц вверх (если эти значения являются отрицательными числами тогда, соответственно, влево и вниз). Очевидно, что при проделанной трансформации вершина параболы функции переместится из точки в точку . Этот факт даёт ещё один способ вычисления координат вершины параболы произвольной квадратичной функции путём приведения её уравнения к виду , позволяющему сразу увидеть координаты вершины параболы — .

Преобразовать произвольную квадратичную функцию вида к форме позволяет метод выделения полного квадрата, использующий формулы сокращённого умножения биномов:
-
- , где и
Сравнивая значения для и , вычисленные дифференциальным методом (см. соответствующий раздел статьи), можно также убедиться, что они являются координатами вершины параболы. В конкретных случаях вовсе не требуется запоминать приведённые громоздкие формулы, удобней всякий раз выполнять преобразования многочлена к желаему виду непосредственно. На конкретном примере этот метод выглядит так:
Недостатком данного метода является его громоздкость, особенно в случае, когда в результате вынесения за скобки приходится работать с дробями. Также он требует определённого навыка в обращении с формулами сокращённого умножения.
Однако, рассмотренное выше доказательство в общем виде приводит к более простому способу вычисления координат вершины параболы с помощью формул и . Например, для той же функции имеем:
- .
Таким образом, .
Нули функции[править | править код]
Число нулей квадратичной функции[править | править код]

Квадратичная функция является целой рациональной функцией второй степени, поэтому она может иметь не более двух нулей в действительной области. В случае расширения на комплексную область можно говорить о том, что квадратичная функция в любом случае имеет ровно два комплексных нуля, которые могут быть строго действительными числами или содержать мнимую единицу.
Определить число нулей квадратичной функции без решения соответствующего квадратного уравнения можно с помощью вычисления дискриминанта. При этом имеются различные вариации его вычисления: обычный (применим всегда), сокращённый (удобен в случае чётного коэффициента ) и приведённый (применим только для приведённого многочлена). При этом числовые значения в каждом случае будут отличаться, однако знак дискриминанта будет совпадать независимо от вариации.
| Полный дискриминант | Сокращённый дискриминант | Приведённый дискриминант |
|---|---|---|
Независимо от вычисления дискриминанта будут справедливы следующие утверждения:
- Если , то функция имеет один нуль кратности 2, который совпадает с абсциссой вершины параболы;
- Если , то функция имеет два действительных нуля и парабола пересекает ось абсцисс в двух точках;
- Если , то функция не имеет действительных нулей (оба её нуля будут комплексными числами), а её график полностью расположен выше оси абсцисс (если ) или лежит целиком ниже неё (если ).
Например, для функции с использованием стандартной формулы для дискриминанта получаем:
- .
Это означает, что данная функция имеет два действительных нуля, то есть её парабола пересекает ось абсцисс в двух точках.
Методы вычисления нулей квадратичной функции[править | править код]
Нахождение нулей квадратичной функции сводится к решению квадратного уравнения , где . Конкретный метод, наиболее подходящий для конкретной квадратичной функции, во многом зависит от его коэффициентов. Во всех специальных случаях кроме специальных формул и методов всегда применима также и универсальная формула. Во всех перечисленных формулах, содержащих квадратный корень, следует учитывать, что если подкоренное выражение является отрицательным числом, то квадратичная функция не имеет нулей в действительной области, а обладает двумя комплексными нулями.
- В наиболее общем случае применяется универсальная формула:
- В случае приведённого уравнения вида , в котором старший коэффициент равен единице, используется упрощённая формула:
- Получить приведённую форму из общей можно, поделив исходное уравнение на . При этом, очевидно, и .
- В случае неполного квадратного уравнения при уравнение принимает степенной вид . Поэтому, воспользовавшись методами решения степенных уравнений, получаем:
- В случае неполного квадратного уравнения при уравнение принимает вид , и для его решения удобно использовать метод факторизации. Вынеся за скобки, получаем . Таким образом, имеем:
Чётность и симметрия квадратичной функции[править | править код]
Симметрия относительно оси ординат[править | править код]

Квадратичная функция является целой рациональной функцией второй степени, поэтому для неё справедливы все соответствующие свойства целой рациональной функции. В частности, она является чётной только тогда, когда в записи её многочлена присутствуют лишь чётные показатели степени, и нечётной — если она содержит только нечётные показатели. Из этого следует, что никакая квадратичная функция не может быть нечётной ввиду того, что на неё изначально накладывается условие , а следовательно она всегда будет содержать чётный показатель 2.
Кроме того, очевидно, что квадратичная функция является чётной только при отсутствии показателя 1, что означает . Этот факт легко доказывается и непосредственно. Так, очевидно, что функция является чётной, так как справедливо:
- , то есть .
Таким образом, квадратичная функция является симметричной относительно оси ординат только тогда, когда . Конкретные значения коэффициентов и на этот факт абсолютно не влияют. В частности, может быть также равно нулю, то есть отсутствовать в записи формулы. В этом случае вершина параболы будет совпадать с началом системы координат.
Во всех других случаях квадратичная функция не будет ни чётной, ни нечётной, то есть является функцией общего вида. Это также легко можно показать с помощью определения чётности функции:
- , то есть .
- , то есть .
Осевая симметрия в общем случае[править | править код]
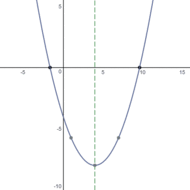
В то же время график любой квадратичной функции обладает осевой симметрией. Как известно, если для некоторой функции для некоторого числа справедливо равенство , то график этой функции обладает осевой симметрией по отношению к прямой . В отношении квадратичной функции таким числом является абсцисса вершины её параболы. Таким образом, график любой квадратичной функции симметричен по отношению к оси, параллельной оси ординат и проходящей через вершину параболы, а осью симметрии функции является прямая .
Доказательство этого факта также не является сложным:
К аналогичному результату приводит и преобразование:
Таким образом, , поэтому график функции симметричен относительно прямой .
Вычисление вершины параболы с помощью нулей функции[править | править код]

Так как ось симметрии параболы всегда проходит через её вершину, то, очевидно, что нули квадратичной функции также всегда симметричны относительно абсциссы вершины параболы. Этот факт позволяет легко вычислить координаты вершины параболы с помощью известных нулей функции. В поле действительных чисел этот способ действует только тогда, когда парабола пересекает ось абсцисс или касается её, то есть имеет нули из действительной области.
В случае, когда квадратичная функция имеет лишь один нуль (кратности 2), то он, очевидно, сам и является вершиной параболы. Если же парабола имеет нули и , то абсцисса её вершины легко вычисляется как среднее арифметическое нулей функции. Ордината вершины вычисляется путём подстановки её абсциссы в исходное уравнение функции:
Особенно удобным этот способ будет в случае, когда квадратичная функция заданна в её факторизированном виде. Так, например, парабола функции будет иметь вершину со следующими координатами:
При этом даже не требуется преобразовывать уравнение функции к общему виду.
Исследование методами дифференциального и интегрального анализа[править | править код]
Производная и первообразная[править | править код]


Как и любая целая рациональная функция квадратичная функция дифференцируема во всей своей области определения. Её производная легко находится с помощью элементарных правил дифференцирования: . Таким образом, видим, что производной квадратичной функции является линейная функция, которая либо строго монотонно возрастает (если ), либо строго монотонно убывает (если ) на всей области определения. При этом также нетрудно заметить, что , что означает, что коэффициент в уравнении исходной функции равен угловому коэффициенту параболы в начале координат.
Квадратичная функция как и любая целая рациональная функция также и интегрируема во всей своей области определения. Её первообразная, очевидно, является кубической функцией:
- , где .
Монотонность и точки экстремума[править | править код]
Очевидно, что вершина параболы является её наивысшей или наинизшей точкой, то есть абсолютным экстремумом квадратичной функции (минимумом при и максимумом при ). Поэтому абсцисса вершины параболы разбивает область определения функции на два монотонных интервала, на одном из которых функция возрастает, а на другом — убывает. Воспользовавшись методами дифференциального исчисления, с помощью этого факта можно легко вывести простую формулу для вычисления координат вершины параболы, заданной общим уравнением , через его коэффициенты.
Согласно необходимому и достаточному условию для существования экстремума, получаем: . При этом , если . Функция является константной функцией, при этом при и при . Таким образом, необходимый и достаточный критерий существования экстремума выполняется в точке . Следовательно, имеем координаты вершины:
Вершина параболы разбивает область определения квадратичной функции на два монотонных интервала: и . При функция на первом из них является строго монотонно убывающей, а на втором — строго монотонно возрастающей. В случае — в точности наоборот.
При этом можно вовсе не запоминать данные формулы, а просто каждый раз пользоваться критериями существования экстремума для каждой конкретной квадратичной функции. Или же рекомендуется запоминать только формулу для вычисления абсциссы вершины параболы. Её ордината легко вычисляется в результате подстановки вычисленной абсциссы в конкретное уравнение функции.
Например, для функции получаем:
- .
Таким образом, вершина параболы данной функции имеет координаты . При этом функция строго монотонно убывает на интервале и строго монотонно возрастает на интервале
Выпуклость и точки перегиба[править | править код]
Так как вторая производная квадратичной функции является константной линейной функцией , то она не имеет точек перегиба, так как её значение постоянно, а соответственно достаточный критерий не будет выполняться ни для какой её точки. Более того, очевидно, что при исходная квадратичная функция будет всюду выпуклой вниз (ввиду того, что её вторая производная всюду положительна), а при — всюду выпуклой вверх (её вторая производная будет всюду отрицательной).
Обратимость квадратичной функции[править | править код]

Так как квадратичная функция не является строго монотонной функцией, то она является необратимой. Так как любую непрерывную функцию, однако, можно обратить на её интервалах строгой монотонности, то для любой квадратичной функции существуют две обратные функции, соответствующие двум её интервалам монотонности. Обратными для квадратичной функции на каждом из её интервалов монотонности являются функции арифметического квадратного корня[2].
Так, функция арифметического квадратного корня является обратной к квадратной функции на интервале . Соответственно, функция является обратной к функции на интервале . Графики функций и будут симметричными друг другу относительно прямой .

Для нахождения обратных функций для произвольной квадратичной функции удобнее представить её в форме , где — вершина её параболы. Далее воспользуемся известным методом для нахождения обратных функций — поменяем местами переменные и и снова выразим через :
Таким образом, обратной к на интервале является функция .
На интервале обратной к является функция .
Например, для функции с вершиной получаем:
- на интервале .
- на интервале .
Примеры появления на практике[править | править код]

- Зависимость пути равноускоренно движущегося (например, высоты свободно падающего) тела от времени.
- Зависимость площади круга от его линейных размеров (например, радиуса).
- Зависимость напора от расхода (напорная характеристика центробежного насоса).
Обобщение[править | править код]
Обобщение на случай многих переменных служат поверхности второго порядка, в общем виде такое уравнение можно записать, как:
- .
Здесь: — матрица квадратичной формы, — постоянный вектор, — константа. Свойства функции, так же как и в одномерном случае, определяются главным коэффициентом — матрицей .
См. также[править | править код]
Примечания[править | править код]
- ↑ Квадратичная функция // Большая школьная энциклопедия. — М. : «Русское энциклопедическое товарищество», 2004. — С. 118—119.
- ↑ Rolf Baumann. Quadratwutzelfunktion // Algebra: Potenzfunktionen, Exponential- und Logarithmusgleichungen, Stochastik : [нем.]. — München : Mentor, 1999. — Т. 9. — С. 17—19. — 167 с. — ISBN 3-580-63631-6.
Литература[править | править код]
- Сканави М.И. График квадратного трёхчлена // Элементарная математика. — 2-е изд., перераб. и доп. — М., 1974. — С. 130—133. — 592 с.
- Каплан И.А. Тридцать третье практическое занятие (экстремум квадратичной функции) // Практические занятия по высшей математике. — 3-е изд. — Харьков, 1974. — С. 449—451.











![{\displaystyle E(f)=\left(-\infty ;-{\frac {b^{2}-4ac}{4a}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/80574007c87fd2e0a084cba4db58f5eaa2f68950)











![{\displaystyle \left(-\infty ;-{\frac {b}{2a}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae6b6c026c5999b70af07f10b99f04c9f3eb4cc4)








































































































![{\displaystyle (-\infty ;0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72c148ad1ad5af487ca5ae78ee670d0d3605a243)













![{\displaystyle (-\infty ;x_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b851e43347b4ceced99ed4c5b14a71e746675021)


![{\displaystyle (-\infty ;-2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/615ae99698f85cb43b3de7eb156149152b51acc6)


