Изоморфизм
Изоморфи́зм (от др.-греч. ἴσος — равный, одинаковый, подобный и μορφή — форма) — соотношение между математическими объектами, выражающее общность их строения; используется в разных разделах математики и в каждом из них определяется в зависимости от структурных свойств изучаемых объектов. Обычно изоморфизм определяется для множеств, наделённых некоторой структурой, например, для групп, колец, линейных пространств; в этом случае он определяется как обратимое отображение (биекция) между двумя множествами со структурой, сохраняющее эту структуру, то есть показывающее, что объекты «одинаково устроены» в смысле этой структуры. Если между объектами существует изоморфизм, то они называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких структур.
Например, два графа называются изоморфными, если между ними существует изоморфизм: то есть вершинам одного графа можно сопоставить вершины другого графа, так чтобы соединённым вершинам первого графа соответствовали соединённые вершины второго графа и наоборот. Иными словами, два графа изоморфны, если они «одинаковы» (с точностью до переименования вершин).
Другим классическим примером изоморфных систем могут служить множество всех вещественных чисел с определённой на нём операцией сложения и множество положительных вещественных чисел с заданной на нём операцией умножения. Отображение в этом случае является изоморфизмом.
Понятие изоморфизма возникло в математике применительно к группам, впоследствии перенесено на другие классы объектов.
Общая алгебра[править | править код]
В общей алгебре изоморфизмом называется обратимое отображение, которое является гомоморфизмом.
Например, для групп и биекция называется изоморфизмом, если для любых выполнено . Если группы являются топологическими, то добавляется условие гомеоморфности соответствующих топологических пространств[1].
Для полей и биекция называется изоморфизмом, если она сохраняет обе операции поля, то есть для любых выполняется:
- ,
- .
Например, факторкольцо для кольца многочленов с вещественными коэффициентами по модулю многочлена является полем, изоморфным[2] полю комплексных чисел :
Для полей с дополнительной структурой (упорядоченные, топологические поля) может добавляться условие, что биекция сохраняет также эти дополнительные структуры.
Наиболее общим образом изоморфизм определяется в теории категорий: объекты категории изоморфны, если между ними существует обратимый морфизм, то есть морфизм , для которого существует такой морфизм , что композиции и — тождественные морфизмы. Определения категории групп, категории колец, категории векторных пространств и других структур строятся таким образом, что классические определения изоморфизма групп, колец, векторных пространств совпадают с общим определением изоморфизма в категории. При этом вводится также понятие изоморфизма категорий — взаимно-однозначного соответствия между категориями с обратимыми функторами.
Теория множеств[править | править код]
В теории множеств любая биекция является изоморфизмом.
К примеру, два частично упорядоченных множества изоморфны, если между ними есть биекция, сохраняющая порядок[3].
Линейные пространства[править | править код]
Два линейных пространства и над одним и тем же полем называются изоморфными, если между векторами и можно установить взаимно однозначное соответствие таким образом, что выполняются условия[4]:
- если вектору соответствует вектор , а вектору соответствует вектор , то вектору соответствует вектор .
- если вектору соответствует вектор , и — элемент поля , то вектору соответствует вектор .
Нормированные пространства[править | править код]
Для нормированных пространств отображение одного из них в другое называется изоморфизмом нормированных пространств, если оно линейно, непрерывно и биективно, и обратное отображение тоже непрерывно. В этом смысле изоморфизм сохраняет структуру линейного пространства и топологию, но не обязательно сохраняет норму. Если изоморфизм ещё и сохраняет норму, то он называется изометрическим изоморфизмом или изометрией[5].
Теория графов[править | править код]
Граф называется изоморфным графу , если существует биекция из множества вершин графа в множество вершин графа , обладающая следующим свойством: если в графе есть ребро из вершины в вершину , то в графе должно быть ребро из вершины в вершину и наоборот — если в графе есть ребро из вершины в вершину , то в графе должно быть ребро из вершины в вершину . В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.
В теории вычислительной сложности до сих пор является открытым вопрос о сложности задачи изоморфности графов. На данный момент не доказана ни её принадлежность классу , ни её -полнота.
Связанные определения[править | править код]
Изоморфизм алгебраической системы на себя называется автоморфизмом. Совокупность всех автоморфизмов некоторой алгебраической системы с операцией композиции и тождественным отображением в качестве нейтрального элемента образует группу. Группа автоморфизмов алгебраической системы обозначается . Наиболее простой пример автоморфизма — это автоморфизм множества, то есть перестановка элементов этого множества.
Любой элемент группы определяет следующий автоморфизм, который называют внутренним автоморфизмом: каждому элементу группы ставится в соответствие сопряжённый ему элемент :
- .
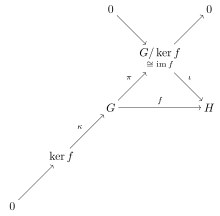
Теоремы об изоморфизме[править | править код]
Теоремы об изоморфизме в алгебре — ряд теорем, связывающих понятия фактора, гомоморфизма и вложенного объекта. Утверждением теорем является изоморфизм некоторой пары групп, колец, модулей, линейных пространств, алгебр Ли или прочих алгебраических структур (в зависимости от области применения). Обычно насчитывают три теоремы об изоморфизме, называемые Первой (также основная теорема о гомоморфизме), Второй и Третьей. Хотя подобные теоремы достаточно легко следуют из определения фактора и честь их открытия никому особо не приписывается, считается, что наиболее общие формулировки дала Эмми Нётер.
Примечания[править | править код]
- ↑ Л. С. Понтрягин Непрерывные группы. С. 392
- ↑ Фаддеев Д. К. Лекции по алгебре. — М.: Наука, 1984. — С. 200—201. — 416 с.
- ↑ Н. К. Верещагин, А. Шень. Лекции по математической логике и теории алгоритмов. Часть 1. Начала теории множеств. стр. 48
- ↑ Шилов Г. Е. Введение в теорию линейных пространств. — М., Л., Гостехтеориздат, 1952. — с. 70
- ↑ Петр Бородин, А. Савчук, И. Шейпак. Задачи по функциональному анализу. — МЦНМО, 2017. — С. 28. — 337 с. — ISBN 9785040485147.
Литература[править | править код]
- Ван дер Варден Б. Л. Алгебра. СПб.: Лань, 2004, 624 стр., ISBN 5-8114-0552-9.
- Понтрягин, Лев Семёнович. Непрерывные группы. — М.: УРСС, 2004. — 520 с. — ISBN 5-354-00957-X.
- Изоморфизм — статья из Математической энциклопедии. О. А. Иванова., Д. М. Смирнов
















![{\displaystyle \mathbb {R} [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/453d1013f9dd290be70d5fe534e0d3311b0a7c6a)


![{\displaystyle \mathbb {R} [x]/(x^{2}+1)\ {\stackrel {\cong }{\longrightarrow }}\ \mathbb {C} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d2571fe31309c19bcacb450e03f879eae04f83)
































