Метод трапеций

Метод трапеций — метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подынтегральной функции на многочлен первой степени, то есть линейную функцию. Площадь под графиком функции аппроксимируется прямоугольными трапециями. Алгебраический порядок точности равен 1.
Если отрезок является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по формуле
Это простое применение формулы для площади трапеции — произведение полусуммы оснований, которыми в данном случае являются значения функции в крайних точках отрезка, на высоту (длину отрезка интегрирования). Погрешность аппроксимации для элементарного отрезка можно оценить через максимум второй производной
(для случаев разбиения отрезка на n частей см. составные формулы ниже).
Составная формула[править | править код]

Если отрезок разбивается узлами интегрирования , , так что и , и на каждом из элементарных отрезков применяется формула трапеций, то суммирование даст составную формулу трапеций
Формула Котеса[править | править код]
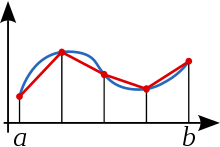
В случае равномерной сетки , где — шаг сетки, составная формула трапеций упрощается:
причём для погрешности справедлива оценка
Свойства[править | править код]
- Метод трапеций быстро сходится для осциллирующих функций, поскольку погрешность за период аннулируется.
- Метод может быть получен путём вычисления среднего арифметического между результатами применения формул правых и левых прямоугольников.
См. также[править | править код]
Литература[править | править код]
- Демидович Б.П., Марон И.А. Основы вычислительной математики. — 2. — Физ-Мат. Лит., 1963. — С. 659.
В другом языковом разделе есть более полная статья Trapezoidal rule (англ.). |
![{\displaystyle \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa)

![{\displaystyle \left|E(f)\right|\leqslant {\frac {\left(b-a\right)^{3}}{12}}\max _{x\in [a,b]}\left|f''(x)\right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1530af4ebda68a7b1473d6db671edbb8434dd1bc)




![{\displaystyle [x_{i},x_{i+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7138606cdb8eb7dddaba59b5aefe1ade6bc05a1b)





