Формула Симпсона

Суть метода — аппроксимация функции f (x) (синий график) квадратичным полиномом P (x) (красный)

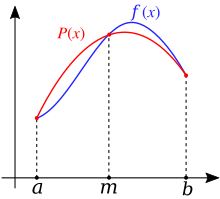
Формула Симпсона (также Ньютона-Симпсона) относится к приёмам численного интегрирования. Получила название в честь британского математика Томаса Симпсона (1710—1761).

Суть приёма заключается в приближении подынтегральной функции на отрезке $[a,b]\,\!$ интерполяционным многочленом второй степени $p_2(x)\,\!$, то есть приближение графика функции на отрезке параболой. Метод Симпсона имеет порядок погрешности 4 и алгебраический порядок точности 3.

Формула

Формулой Симпсона называется интеграл от интерполяционного многочлена второй степени на отрезке $[a,b]$:

${\int\limits_a^b f(x) dx} \approx {\int\limits_{a}^{b} {p_2(x)} dx} = \frac{b-a}{6}{ \left( f(a) + 4 f\left(\frac{a+b}{2}\right) + f(b) \right)},$

где $f(a)$, $f((a+b)/2)$ и $f(b)$ — значения функции в соответствующих точках (на концах отрезка и в его середине).

Погрешность

При условии, что у функции $f(x)$ на отрезке $[a,b]$ существует четвёртая производная, погрешность $E(f)$, согласно найденной Джузеппе Пеано формуле равна:

$E(f) = - \frac{(b-a)^5}{2880}{{f^{(4)}(\zeta)}}, \ \ \ \zeta \in [a,b].$

В связи с тем, что значение $\zeta$ зачастую неизвестно, для оценки погрешности используется следующее неравенство:

$\left| E(f) \right| \le \frac{(b-a)^5}{2880} \max\limits_{x\in[a,b]} {\left| f^{(4)}(x) \right|}.$

Представление в виде метода Рунге-Кутта

Формулу Симпсона можно представить в виде таблицы метода Рунге-Кутты следующим образом:

$\begin{array}{c|ccc} 0 &&&\\ \frac{1}{2} & \frac{1}{2} &&\\ 1 & -1 & 2&\\ \hline & \frac{1}{6} & \frac{2}{3} & \frac{1}{6} \end{array}$

Составная формула (формула Котеса)

Для более точного вычисления интеграла, интервал $[a,b]$ разбивают на $N$ отрезков одинаковой длины и применяют формулу Симпсона на каждом из них. Значение исходного интеграла является суммой результатов интегрирования на всех отрезках.

${\int\limits_a^b f(x) dx} \approx \frac h6 \cdot \left( f(x_0)+2\sum_{k=1}^{N-1}f(x_k)+4\sum_{k=1}^{N}f \left( \frac{x_{k-1}+x_k}2 \right)+f(x_N) \right)$

где $h = \frac{b-a}{N}$ — величина шага, а $x_k=a+k h\,\!$ — узлы интегрирования, границы элементарных отрезков, на которых применяется формула Симпсона. Обычно для равномерной сетки данную формулу записывают в других обозначениях (отрезок $[a,b]\,\!$ разбит на $2N\,\!$ узлов) в виде

$\int\limits_a^b f(x) dx \approx \frac{h}{6}\left(f_0 + 4 \left(f_1 + f_3 + \ldots +f_{2N-1}\right) + 2 \left(f_2 + f_4 + ... +f_{2N-2}\right) + f_{2N}\right).$

Также формулу можно записать используя только известные значения функции, т.е. значения в узлах:

${\int\limits_a^b f(x) dx} \approx \frac h6 \cdot \sum_{k=1,2}^{N-1} \left( f(x_{k-1})+4f(x_k)+f(x_{k+1}) \right)$

где $k=1,2$ означает что индекс меняется от единицы с шагом, равным двум.

Общая погрешность $E(f)$ при интегрировании по отрезку $[a,b]\,\!$ с шагом $x_i - x_{i-1} = h$ (при этом, в частности, $x_0 = a$, $x_N = b$) определяется по формуле:

$\left| E(f) \right| \le \frac{(b-a)}{2880}h^4 \max\limits_{x\in[a,b]} |f^{(4)} (x)|$.

При невозможности оценить погрешность с помощью максимума четвёртой производной (например, на заданном отрезке она не существует, либо стремится к бесконечности), можно использовать более грубую оценку:

$\left| E(f) \right| \le \frac{(b-a)}{288}h^3 \max\limits_{x\in[a,b]} |f^{(3)} (x)|$.

Литература

• Костомаров Д. П., Фаворский А. П. «Вводные лекции по численным методам»