Нечёткая логика

Нечёткая логика (англ. fuzzy logic) — раздел математики, являющийся обобщением классической логики и теории множеств, базирующийся на понятии нечёткого множества, впервые введённого Лотфи Заде в 1965 году как объекта с функцией принадлежности элемента ко множеству, принимающей любые значения на отрезке $[0,1]$, а не только $0$ или $1$. На основе этого понятия вводятся различные логические операции над нечёткими множествами и формулируется понятие лингвистической переменной, в качестве значений которой выступают нечёткие множества.

Предметом нечёткой логики считается исследование рассуждений в условиях нечёткости, размытости, сходных с рассуждениями в обычном смысле, и их применение в вычислительных системах.

Направления исследований нечёткой логики

В настоящее время^{[уточнить]} существует по крайней мере два основных направления научных исследований в области нечёткой логики:

• нечёткая логика в широком смысле (теория приближённых вычислений);
• нечёткая логика в узком смысле (символическая нечёткая логика).

Математические основы

Символическая нечёткая логика

Символическая нечёткая логика основывается на понятии t-нормы. После выбора некоторой t-нормы (а её можно ввести несколькими разными способами) появляется возможность определить основные операции над пропозициональными переменными: конъюнкцию, дизъюнкцию, импликацию, отрицание и другие.

Нетрудно доказать теорему о том, что дистрибутивность, присутствующая в классической логике, выполняется только в случае, когда в качестве t-нормы выбирается t-норма Гёделя^{[уточнить]}.

Кроме того, в силу определённых причин, в качестве импликации чаще всего выбирают операцию, называемую residium (она, вообще говоря, также зависит от выбора t-нормы).

Определение основных операций, перечисленных выше, приводит к формальному определению базисной нечёткой логики, которая имеет много общего с классической булевозначной логикой (точнее, с исчислением высказываний).

Существуют три основных базисных нечётких логики: логика Лукасевича, логика Гёделя и вероятностная логика (англ. product logic). Интересно, что объединение любых двух из трёх перечисленных выше логик приводит к классической булевозначной логике.

Синтез функций непрерывной логики заданных таблично

Функция нечёткой логики Заде всегда принимает значение одного из своих аргументов либо его отрицания. Таким образом, функцию нечёткой логики можно задать таблицей выбора, в которой перечислены все варианты упорядочения аргументов и отрицаний, и для каждого варианта указано значение функции. Например, строка таблицы функции двух аргументов может иметь следующий вид:

$x_{1}\leq x_{2}\leq {\bar {x}}_{2}\leq {\bar {x}}_{1}:x_{2}$.

Однако произвольная таблица выбора не всегда задаёт функцию нечёткой логики. В работе был сформулирован критерий, позволяющий установить является ли функция, заданная таблицей выбора, функцией нечёткой логики и предложен простой алгоритм синтеза, основанный на введённых концепциях конституент минимума и максимума. Функция нечёткой логики представляет собой дизъюнкцию конституент минимума, где конституента максимума — это конъюнкция переменных текущей области больших либо равных значению функции в этой области (справа от значения функции в неравенстве, включая значение функции). Например, для указанной строки таблицы конституента минимума имеет вид $x_{2}{\bar {x}}_{2}{\bar {x}}_{1}$.

Теория приближённых вычислений

Основное понятие нечёткой логики в широком смысле — нечёткое множество, определяемое при помощи обобщённого понятия характеристической функции. Затем вводятся понятия объединения, пересечения и дополнения множеств (через характеристическую функцию; задать можно различными способами), понятие нечёткого отношения, а также одно из важнейших понятий — понятие лингвистической переменной.

Вообще говоря, даже такой минимальный набор определений позволяет использовать нечёткую логику в некоторых приложениях, для большинства же необходимо задать ещё и правило вывода (и оператор импликации).

Нечёткая логика и нейронные сети

Поскольку нечёткие множества описываются функциями принадлежности, а t-нормы и k-нормы обычными математическими операциями, можно представить нечёткие логические рассуждения в виде нейронной сети. Для этого функции принадлежности надо интерпретировать как функции активации нейронов, передачу сигналов как связи, а логические t-нормы и k-нормы, как специальные виды нейронов, выполняющие математические соответствующие операции. Существует большое разнообразие подобных нейро-нечётких сетей (neuro-fuzzy network (англ.)) . Например, ANFIS (Adaptive Neuro fuzzy Inference System) — адаптивная нейро-нечеткая система вывода. (англ.)

Она может быть описана в универсальной форме аппроксиматоров как

$y(x)=\sum _{i=1}^{N}\phi _{i}(x)*\theta _{i}$,

кроме того, этой формулой могут быть описаны также некоторые виды нейронных сетей, такие как радиально базисные сети (RBF), многослойные персептроны (MLP), а также вейвлеты и сплайны.

Примеры

Нечёткое множество, содержащее число 5

Нечёткое множество, содержащее число 5, можно задать, например, такой характеристической функцией: $\mu _{A}\left(x\right)=\left(1+\left|x-5\right|^{n}\right)^{-1}$

Пример определения лингвистической переменной

В обозначениях, принятых для лингвистической переменной:

• X = «Температура в комнате»
• U = [5, 35]
• T = {«холодно», «тепло», «жарко»}

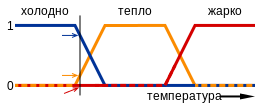
Характеристические функции:

• $\mu _{cold}\left(u\right)={\frac {1}{1+\left({\frac {u-10}{7}}\right)^{12}}}$
• $\mu _{ok}\left(u\right)={\frac {1}{1+\left({\frac {u-20}{3}}\right)^{6}}}$
• $\mu _{hot}\left(u\right)={\frac {1}{1+\left({\frac {u-30}{6}}\right)^{10}}}$

Правило G порождает новые термы с использованием союзов «и», «или», «не», «очень», «более или менее».

• не A: $1-\mu _{A}\left(u\right)$
• очень A: $\left(\mu _{A}\left(u\right)\right)^{2}$
• более или менее A: ${\sqrt {\mu _{A}\left(u\right)}}$
• A или B: $\max \left(\mu _{A}\left(x\right),\mu _{B}\left(x\right)\right)$
• A и B: $\min \left(\mu _{A}\left(x\right),\mu _{B}\left(x\right)\right)$

Нечёткая логика в информатике

Нечёткая логика — набор нестрогих правил, в которых для достижения поставленной цели могут использоваться радикальные идеи, интуитивные догадки, а также опыт специалистов, накопленный в соответствующей области. Нечёткой логике свойственно отсутствие строгих стандартов. Чаще всего она применяется в экспертных системах, нейронных сетях и системах искусственного интеллекта. Вместо традиционных значений Истина и Ложь в нечёткой логике используется более широкий диапазон значений, среди которых Истина, Ложь, Возможно, Иногда, Не помню (Как бы Да, Почему бы и Нет, Ещё не решил, Не скажу…). Нечёткая логика просто незаменима в тех случаях, когда на поставленный вопрос нет чёткого ответа (да или нет; «0» или «1») или наперёд неизвестны все возможные ситуации. Например, в нечёткой логике высказывание вида «X есть большое число» интерпретируется как имеющее неточное значение, характеризуемое некоторым нечётким множеством. «Искусственный интеллект и нейронные сети — это попытка смоделировать на компьютере поведение человека. А так как люди редко видят окружающий мир лишь в чёрно-белом цвете, возникает необходимость в использовании нечёткой логики».

Литература

• Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. — М.: Мир, 1976. — 166 с.
• Леоненков А. В. Нечеткое моделирование в среде MATLAB и fuzzyTECH. –– СПб.: БХВ Петербурr, 2005. –– 736 с.: ил.
• Орлов А. И. Задачи оптимизации и нечеткие переменные. — М.: Знание, 1980. — 64 с.
• Зак Юрий Александрович. Принятие решений в условиях нечетких и размытых данных: Fuzzy-технологии. — М.: «ЛИБРОКОМ», 2013. — 352 с. — ISBN 978-5-397-03451-7.
• Бочарников В. П. Fuzzy-технология: Математические основы. Практика моделирования в экономике.. — М.: Мир, 2001. — 328 с. — ISBN 966-521-082-3.
• Тэрано, Т., Асаи, К., Сугэно, М. Прикладные нечёткие системы. — М.: Мир, 1993. — 368 с.
• Новак В., Перфильева И., Мочкрож И. Математические принципы нечёткой логики = Mathematical Principles of Fuzzy Logic. — Физматлит, 2006. — 352 с. — ISBN 0-7923-8595-0.
• Рутковский Лешек. Искусственные нейронные сети. Теория и практика. — М.: Горячая линия - Телеком, 2010. — 520 с. — ISBN 978-5-9912-0105-6.
• Усков А. А., Кузьмин А. В. Интеллектуальные технологии управления. Искусственные нейронные сети и нечеткая логика. — М.: Горячая Линия — Телеком, 2004. — 143 с.
• Круглов В. В. Дли М. И. Голунов Р. Ю. Нечёткая логика и искусственные нейронные сети. М.: Физматлит, 2001. 221с.
• Дьяконов В. П., Круглов В. В. MATLAB. Математические пакеты расширения. Специальный справочник. СПб.: Питер, 2001. 480с (имеются главы по нечёткой логике и нейронным сетям).
• Дьяконов В. П., Абраменкова И. В., Круглов В. В. MATLAB 5 с пакетами расширений. Под редакцией проф. В. П. Дьяконова. М.: Нолидж, 2001. 880с (имеются главы по нечёткой логике и нейронным сетям).
• Дьяконов В. П., Круглов В. В. MATLAB 6.5 SP1/7/7 SP1/7 SP2+Simulink 5/6. Инструменты искусственного интеллекта и биоинформатики. М.: СОЛОН-Пресс, 2006. 456с.
• Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы: Пер. с польского И. Д. Рудинского. М.: Горячая линия — Телеком, 2004. — 452 с. ISBN 5-93517-103-1
• Штовба С. Д. Проектирование нечетких систем средствами MATLAB. М.: Горячая линия — Телеком.- 2007.- 288 c.
• Uziel Sandler, Lev Tsitolovsky Neural Cell Behavior and Fuzzy Logic. Springer, 2008. — 478 с. ISBN 978-0-387-09542-4
• Орловский С. А. Проблемы принятия решений при нечеткой исходной информации. — М.: Наука, 1981. — 208 с. — 7600 экз.
• Орлов А. И., Луценко Е. В. Системная нечеткая интервальная математика. — Монография (научное издание). — Краснодар, КубГАУ. 2014. — 600 с.[1]
• Орлов А. И., Луценко Е.В. Анализ данных, информации и знаний в системной нечеткой интервальной математике: научная монография. – Краснодар: КубГАУ, 2022. – 405 с. [2]

Ссылки

• Статьи и доклады Лотфи Заде  (неопр.). Дата обращения: 18 января 2010. Архивировано из оригинала 15 декабря 2005 года.
• Нечеткая логика, мягкие вычисления и вычислительный интеллект  (неопр.). Дата обращения: 18 января 2010. Архивировано 6 марта 2010 года.
• Учебник по математической логике, содержащий и главу о нечеткой логике  (рус.). Дата обращения: 8 января 2009. Архивировано из оригинала 27 сентября 2007 года.
• Информационно-методический портал кафедры ИПМ (Информатика и прикладная математика)  (рус.). — Ранее "Сайт, посвященный нечеткой логике". Разделы доступны только для зарегистрированных пользователей. Дата обращения: 8 января 2009. Архивировано 13 февраля 2012 года.
• Сергей Гриняев. Нечеткая логика в системах управления  (рус.) (html). Компьютерра–Онлайн (8 октября 2001). — Статья в журнале Компьютерра. Дата обращения: 8 января 2009. Архивировано 19 сентября 2016 года.
• Fuzzy Logic Toolbox (англ.). — Дополнение к MATLAB для моделирования систем с нечёткой логикой. Дата обращения: 8 января 2009. Архивировано 13 февраля 2012 года.
• Fuzzy Logic Toolbox - Проектирование систем управления  (рус.) (html). Экспонента.ру. Дата обращения: 8 января 2009. Архивировано 27 мая 2007 года.
• [3] Архивная копия от 11 февраля 2015 на Wayback Machine Научные статьи по нечёткой логике.