Полярная система координат

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой декартовой, или прямоугольной, системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
Полярная система координат задаётся лучом, который называют нулевым лучом, или полярной осью. Точка, из которой выходит этот луч, называется началом координат, или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается ) соответствует расстоянию от точки до начала координат. Угловая координата также называется полярным углом, или азимутом, и обозначается , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку[1].
Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.
История[править | править код]
Понятие угла и радиуса были известны ещё в первом тысячелетии до нашей эры. Греческий астроном Гиппарх (190—120 до н. э.) создал таблицу, в которой для разных углов приводились длины хорд. Существуют свидетельства применения им полярных координат для определения положения небесных тел[2]. Архимед в своём сочинении «Спирали» описывает так называемую спираль Архимеда, функцию, радиус которой зависит от угла. Работы греческих исследователей, однако, не развились в целостное определение системы координат.
В IX веке персидский математик Хаббаш аль-Хасиб (аль-Марвази́) применял методы картографических проекций и сферической тригонометрии для преобразования полярных координат в другую систему координат с центром в некоторой точке на сфере, в этом случае, для определения Киблы — направления на Мекку[3]. Персидский астроном Абу Райхан Бируни (973—1048) выдвинул идеи, которые выглядят как описание полярной системы координат. Он был первым, кто, примерно в 1025 году, описал полярную экви-азимутальную равнопромежуточную проекцию небесной сферы[4].
Существуют разные версии о введении полярных координат в качестве формальной системы координат. Полная история возникновения и исследования описана в работе профессора из Гарварда Джулиан Лоувел Кулидж «Происхождение полярных координат»[5]. Грегуар де Сен-Венсан и Бонавентура Кавальери независимо друг от друга пришли к похожей концепции в середине XVII века. Сен-Венсан описал полярную систему в личных заметках в 1625 году, напечатав свои труды в 1647; а Кавальери напечатал свои труды в 1635 году, и исправленную версию в 1653 году. Кавальери применял полярные координаты для вычисления площади, ограниченной спиралью Архимеда. Блез Паскаль впоследствии использовал полярные координаты для вычисления длин параболических дуг.
В книге «Метод флюксий» (англ. Method of Fluxions, написана в 1671 году, напечатана в 1736 году) сэр Исаак Ньютон исследовал преобразование между полярными координатами, которые он обозначал как «Седьмой способ; Для спиралей» («англ. Seventh Manner; For Spirals»), и девятью другими системами координат[6]. В статье, опубликованной в 1691 году в журнале Acta eruditorum, Якоб Бернулли использовал систему с точкой на прямой, которые он назвал полюсом и полярной осью соответственно. Координаты задавались как расстояние от полюса и угол от полярной оси. Работа Бернулли была посвящена проблеме нахождения радиуса кривизны кривых, определённых в этой системе координат.
Введение термина «полярные координаты» приписывают Грегорио Фонтана. В XVIII веке он входил в лексикон итальянских авторов. В английский язык термин попал через перевод трактата Сильвестра Лакруа «Дифференциальное и интегральное исчисление», выполненного в 1816 году Джорджем Пикоком[7][8] Для трёхмерного пространства полярные координаты впервые предложил Алекси Клеро, а Леонард Эйлер был первым, кто разработал соответствующую систему[5].
Графическое представление[править | править код]

Каждая точка в полярной системе координат может быть определена двумя полярными координатами, что обычно называются (радиальная координата, встречается вариант обозначения ) и (угловая координата, полярный угол, фазовый угол, азимут, позиционный угол, иногда пишут или ). Координата соответствует расстоянию от точки до центра, или полюса системы координат, а координата равна углу, отсчитываемому в направлении против часовой стрелки от луча через 0° (иногда называемого полярной осью системы координат)[1].
Полярный радиус определён для любой точки плоскости и всегда принимает неотрицательные значения . Полярный угол определён для любой точки плоскости, за исключением полюса , и принимает значения . Полярный угол измеряется в радианах и отсчитывается от полярной оси:
- в положительном направлении (против направления движения часовой стрелки), если значение угла положительное;
- в отрицательном направлении (по направлению движения часовой стрелки), если значение угла отрицательное.
Например, точка с координатами будет выглядеть на графике как точка на луче, который лежит под углом 60° к полярной оси, на расстоянии 3 единиц от полюса. Точка с координатами будет нарисована на том же месте.
Одной из важных особенностей полярной системы координат является то, что одна и та же точка может быть представлена бесконечным количеством способов. Это происходит потому, что для определения азимута точки нужно повернуть полярную ось так, чтобы она указывала на точку. Но направление на точку не изменится, если осуществить произвольное число дополнительных полных оборотов. В общем случае точка может быть представлена в виде или , где — произвольное целое число[9].
Для обозначения полюса используют координаты . Независимо от координаты точка с нулевым расстоянием от полюса всегда находится на нём[10]. Для получения однозначных координат точки, обычно следует ограничить значение расстояния до неотрицательных значений , а угол к интервалу или (в радианах или )[11].
Углы в полярных координатах задаются либо в градусах, либо в радианах, при этом . Выбор, как правило, зависит от области применения. В навигации традиционно используют градусы, в то время как в некоторых разделах физики и почти во всех разделах математики используют радианы[12].
Связь между декартовыми и полярными координатами[править | править код]
Пару полярных координат и можно перевести в Декартовы координаты и путём применения тригонометрических функций синуса и косинуса (при этом предполагается, что нулевой луч полярной системы координат совпадает с осью декартовой системы):
в то время как две декартовы координаты и могут быть переведены в полярную координату :
- (по теореме Пифагора).
Для определения угловой координаты следует принять во внимание два следующих соображения:
- Для , может быть произвольным действительным числом.
- Для , чтобы получить уникальное значение , следует ограничиться интервалом в . Обычно выбирают интервал или .
Для вычисления в интервале , можно воспользоваться такими уравнениями ( обозначает обратную функцию к тангенсу):
- .
Для вычисления в интервале , можно воспользоваться такими уравнениями:[13]
- .
Учитывая, что для вычисления полярного угла недостаточно знать отношение к , а ещё нужны знаки одного из этих чисел, многие из современных языков программирования имеют среди своих функций помимо функции atan, определяющей арктангенс числа, ещё и дополнительную функцию atan2, которая имеет отдельные аргументы для числителя и знаменателя. В языках программирования, поддерживающих необязательные аргументы (например, в Common Lisp), функция atan может получать значение координаты . Однако можно заметить, что независимо от знаков декартовых координат, частные производные угла по ним вычисляются довольно просто, благодаря чему получаем удобные матрицы Якоби:
Уравнение кривых в полярных координатах[править | править код]
Благодаря радиальной природе полярной системы координат, некоторые кривые могут быть достаточно просто описаны полярным уравнением, тогда как уравнение в прямоугольной системе координат было бы намного сложнее. Среди самых известных кривых: полярная роза, архимедова спираль, Лемниската, улитка Паскаля и кардиоида.
Окружность[править | править код]

Общее уравнение окружности с центром в () и радиусом имеет вид:
Это уравнение может быть упрощено для частных случаев, например
является уравнением, определяющим окружность с центром в полюсе и радиусом [14].
Прямая[править | править код]
Радиальные прямые (те, которые проходят через полюс) определяются уравнением
- ,
где — угол, на который прямая отклоняется от полярной оси, то есть, , где — наклон прямой в прямоугольной системе координат. Нерадиальная прямая, перпендикулярно пересекает радиальную прямую в точке определяется уравнением
Полярная роза[править | править код]

Полярная роза — известная математическая кривая, похожая на цветок с лепестками. Она может быть определена простым уравнением в полярных координатах:
для произвольной постоянной (включая 0). Если — целое число, то это уравнение будет определять розу с лепестками для нечётных , либо с лепестками для чётных . Если — рациональное, но не целое, график, заданный уравнением, образует фигуру, подобную розе, но лепестки будут перекрываться. Если — иррациональное, то роза состоит из бесконечного множества частично накладывающихся друг на друга лепестков. Розы с 2, 6, 10, 14 и т. д. лепестками этим уравнением определить невозможно. Переменная определяет длину лепестков.
Если считать, что радиус не может быть отрицательным, то при любом натуральном мы будем иметь -лепестковую розу. Таким образом, уравнение будет определять розу с двумя лепестками. С геометрической точки зрения радиус — это расстояние от полюса до точки и он не может быть отрицательным.
Спираль Архимеда[править | править код]

Архимедова спираль названа в честь её изобретателя, древнегреческого математика Архимеда. Эту спираль можно определить с помощью простого полярного уравнения:
Изменения параметра приводят к повороту спирали, а параметра — расстояния между витками, которое является константой для конкретной спирали. Спираль Архимеда имеет две ветви, одну для а другую для . Две ветви плавно соединяются в полюсе. Зеркальное отображение одной ветви относительно прямой, проходящей через угол 90°/270°, даст другую ветвь. Эта кривая интересна тем, что была описана в математической литературе одной из первых, после конического сечения, и лучше других определяется именно полярным уравнением.
Конические сечения[править | править код]

Коническое сечение, один из фокусов которого находится в полюсе, а другой где-то на полярной оси (так, что большая полуось лежит вдоль полярной оси) задаётся уравнением:
- ,
где — эксцентриситет, а — фокальный параметр. Если , это уравнение определяет гиперболу; если , то параболу; если , то эллипс. Отдельным случаем является , определяющее окружность с радиусом .
Комплексные числа[править | править код]


Каждое комплексное число может быть представлено точкой на комплексной плоскости, и, соответственно, эта точка может определяться в декартовых координатах (прямоугольная или декартова форма), либо в полярных координатах (полярная форма). Комплексное число может быть записано в прямоугольной форме так:
- ,
где — мнимая единица, или в полярной (см. формулы преобразования между системами координат выше):
и отсюда:
- ,
где — число Эйлера. Благодаря формуле Эйлера, оба представления эквивалентны[15] (В этой формуле, подобно остальным формулам, содержащим возведения в степень углов, угол задан в радианах)
Для перехода между прямоугольным и полярным представлением комплексных чисел, могут использоваться указанные выше формулы преобразования между системами координат.
Операции умножения, деления и возведения в степень с комплексными числами, как правило, проще проводить в полярной форме. Согласно правилам возведения в степень:
- Умножение:
- Деление:
- Возведение в степень (формула Муавра):
В математическом анализе[править | править код]
Операции математического анализа тоже можно сформулировать, используя полярные координаты[16][17].
Дифференциальное исчисление[править | править код]
Справедливы следующие формулы:
Чтобы найти тангенс угла наклона касательной к любой данной точке полярной кривой в декартовых координатах, выразим их через систему уравнений в параметрическом виде:
Дифференцируя оба уравнения по получим:
Разделив эти уравнения (второе на первое), получим искомый тангенс угла наклона касательной в декартовой системе координат в точке :
Интегральное исчисление[править | править код]

Пусть — область, которую образуют полярная кривая и лучи и , где . Тогда площадь этой области находится определённым интегралом:

Такой результат можно получить следующим образом. Сначала разобьём интервал на произвольное число подынтервалов . Таким образом, длина такого подынтервала равна (полная длина интервала), разделённая на (число подынтервалов). Пусть для каждого подынтервала — средняя точка. Построим секторы с центром в полюсе, радиусами , центральными углами и длиной дуги . Поэтому площадь каждого такого сектора будет . Отсюда, полная площадь всех секторов:
Если число подынтервалов увеличивать, то погрешность такого приближенного выражения будет уменьшаться. Положив , полученная сумма станет интегральной. Предел этой суммы при определяет вышеописанный интеграл:
Обобщение[править | править код]
Используя декартовы координаты, площадь бесконечно малого элемента может быть вычислена как . При переходе к другой системе координат в многократных интегралах необходимо использовать определитель Якоби:
Для полярной системы координат, определитель матрицы Якоби равен :
Следовательно, площадь элемента в полярных координатах можно записать так:
Теперь, функция, записанная в полярных координатах, может быть интегрирована следующим образом:
Здесь область , как и в предыдущем разделе, такая, которую образуют полярная кривая и лучи и .
Формула для вычисления площади, описанная в предыдущем разделе, получена в случае . Интересным результатом применения формулы для многократных интегралов является Интеграл Эйлера — Пуассона:
Векторный анализ[править | править код]
Для полярных координат можно применить элементы векторного анализа. Любое векторное поле на двумерном пространстве (плоскости) можно записать в полярной системе координат, используя единичные векторы:
в направлении , и
Связь между декартовыми компонентами поля и и его компонентами в полярной системе координат задаётся уравнениями:
Соответствующим образом в полярной системе координат определяются операторы векторного анализа. Например, градиент скалярного поля записывается:
Всё это работает за исключением одной особой точки — полюса, для которой не определено, и векторный базис, описанный выше, построить таким образом в данной точке нельзя. Это надо иметь в виду, хотя на практике векторные поля, исследуемые с помощью полярных координат, часто или сами имеют особенность в этой точке, или равны в ней нулю, что несколько облегчает дело. Кроме того, использование полярных координат никак не затрудняет выражение произвольного векторного поля сколь угодно близко к этой точке.
Трёхмерное расширение[править | править код]
Полярная система координат распространяется в третье измерение двумя системами: цилиндрической и сферической, обе содержат двумерную полярную систему координат как подмножество. По сути, цилиндрическая система расширяет полярную добавлением ещё одной координаты расстояния, а сферическая — ещё одной угловой координаты.
Цилиндрические координаты[править | править код]

Цилиндрическая система координат, грубо говоря, расширяет плоскую полярную систему добавлением третьей линейной координаты, называемой «высотой» и равной высоте точки над нулевой плоскостью подобно тому, как декартова система расширяется на случай трёх измерений. Третья координата обычно обозначается как , образуя тройку координат .
Тройку цилиндрических координат можно перевести в декартову систему следующими преобразованиями:
Сферические координаты[править | править код]
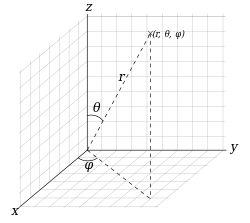
Также полярные координаты можно расширить на случай трёх измерений путём добавления угловой координаты , равным углу поворота от вертикальной оси (называется зенитом или широтой, значения находятся в интервале от 0 до 180°). То есть, сферические координаты, это тройка , где — расстояние от центра координат, — угол от оси (как и в плоских полярных координатах), — широта. Сферическая система координат подобна географической системе координат для определения места на поверхности Земли, где начало координат совпадает с центром Земли, широта является дополнением и равна , а долгота вычисляется по формуле [18].
Тройку сферических координат можно перевести в декартову систему следующими преобразованиями:
Обобщение на n измерений[править | править код]
Полярную систему координат можно расширить на случай -мерного пространства. Пусть , — координатные векторы -мерной прямоугольной системе координат. Необходимые координаты в -мерный полярной системе можно вводить как угол отклонения вектора от координатной оси .
Для перевода обобщённых -мерных полярных координат в декартовы можно воспользоваться следующими формулами:
Как можно показать, случай соответствует обычной полярной системе координат на плоскости, а — обычной сферической системе координат.
Якобиан преобразования полярных координат в декартовы даётся формулой:
- ,
где -мерный элемент объёма имеет вид:
Применение[править | править код]
Полярная система координат двумерная и поэтому может применяться только в тех случаях, когда местонахождение точки определяется на плоскости, или для случая однородности свойств системы в третьем измерении, например, при рассмотрении течения в круглой трубе. Лучшим контекстом применения полярных координат являются случаи, тесно связанные с направлением и расстоянием от некоторого центра. Например, в приведённых выше примерах видно, что простых уравнений в полярных координатах достаточно для определения таких кривых как спираль Архимеда, уравнения которых в прямоугольной системе координат гораздо сложнее. Кроме того, многие физические системы — такие, которые содержат тела, движущиеся вокруг центра, либо явления, распространяющиеся из некоторого центра — гораздо проще моделировать в полярных координатах. Поводом создания полярной системы координат было исследование орбитального и движения по кругу, впоследствии оказалось, что она крайне удобна иногда и для исследования некругового движения (см. Кеплерова задача).
Позиционирование и навигация[править | править код]
Полярную систему координат часто применяют в навигации, поскольку пункт назначения можно задать как расстояние и направление движения от отправной точки. Например, в авиации, для навигации применяют несколько изменённую версию полярных координат. В этой системе, обычно используемой для навигации, луч 0° называют направлением 360, а углы отсчитываются в направлении по часовой стрелке. Направление 360 соответствует магнитному северу, а направления 90, 180, и 270 соответствуют магнитным востоку, югу и западу[19]. Так, самолёт, летящий 5 морских миль на восток можно описать как самолёт, летящий 5 единиц в направлении 90 (центр управления полётами назовёт его найн-зиро)[20].
Применение в физике[править | править код]

Системы с радиальной симметрией очень хорошо подходят для описания в радиальных координатах, где полюс системы координат совпадает с центром симметрии. В качестве примера можно привести уравнение тока грунтовых вод в случае радиально симметричных колодцев. Системы с центральными силами также подходят для моделирования в полярных координатах. К таким системам относятся гравитационные поля, подчиняющиеся закону обратно-квадратичной зависимости, и вообще центральные силы. Также существенное удобство полярные координаты предоставляют при работе с системами, имеющими точечные (или приближенно точечные) источники энергии, такие как радиоантенны — при исследовании их излучения на сравнительно больших расстояниях от антенны, распространение звука или света — в особенности (но не обязательно) сферически- или цилиндрически-симметричное. В определённых задачах, в том числе из числа упомянутых выше, использование сферических или цилиндрических координат (являющихся для этих задач естественными) по сути сводится к использованию просто двумерных полярных координат.
Полярные координаты как для вычислений, так и для наглядного изображения их результатов, бывают достаточно полезны не только в случаях, когда симметрия задачи близка в целом к осевой или сферической, но и в случаях, когда симметрия явно далека от таковой, например, для вычисления поля диполя. В этом случае применение полярных координат имеет мотивировку в малом размере источника поля (заряды диполя расположены очень близко друг к другу), к тому же поле каждого такого заряда просто выражается в полярных координатах, особенно если поместить полюс в один из этих зарядов (поле второго будет отличаться, кроме знака, лишь на малую поправку).
В квантовой механике и химии полярные координаты (наряду со сферическими для более сложных случаев) используются для изображения угловой зависимости волновой функции электрона в атоме, в том числе в целях качественного анализа и наглядности при преподавании.
Применение в прикладных целях, диаграммы направленности[править | править код]


В разных прикладных областях, полярные координаты применяются как способами, близкими к применяемым в соответствующих областям фундаментальной физики, так и самостоятельным образом.
Трёхмерное моделирование звука динамиков может использоваться для прогнозирования их эффективности. Необходимо сделать несколько диаграмм в полярных координатах для широкого диапазона частот, поскольку фронт существенно меняется в зависимости от частоты звука. Полярные диаграммы помогают увидеть, что многие громкоговорители с понижением частоты звука теряют направленность. В случае излучателя, имеющего строгую осевую симметрию или слабо от неё отклоняющегося, достаточно использовать не сферические, а обычные (двумерные) полярные координаты, так как во всех плоскостях, проходящих через ось симметрии, зависимость будет одинаковой или почти одинаковой. Если такой симметрии нет, то какое-то представление о звуковом потоке в разных направлениях может дать пара (для каждой частоты) полярных диаграмм в перпендикулярных плоскостях, для эллиптического или прямоугольного излучателя — связанного с его главными осями.
В полярных координатах также принято представлять характеристику направленности микрофонов, определяемую отношением чувствительности при падении звуковой волны под углом относительно акустической оси микрофона к его осевой чувствительности.
В принципе, полярные диаграммы могут использоваться для представления практически любых зависимостей. Но на практике обычно этот вид представления выбирается в случаях, когда речь идет от зависимости от реального геометрического направления (см. например Роза ветров, Диаграмма рассеяния, зависимость отраженного светового потока от угла в фотометрии, диаграмма направленности антенн, светодиодов и других светоизлучателей, фотодатчиков, акустических систем итп). Также довольно нередко можно встретиться с применением полярных координат в случаях, когда одна из переменных имеет циклический характер (в полярных координатах её довольно естественно представлять углом).
Могут применяться и областях, не связанных прямо с физикой (хотя иногда можно проследить более или менее прямую аналогию в этом плане), например, можно использовать полярные диаграммы, аналогичные розе ветров, например, для изучения направлений миграций животных. Такое использование достаточно удобно и наглядно.
См. также[править | править код]
Примечания[править | править код]
- ↑ 1 2 Brown, Richard G. Advanced Mathematics: Precalculus with Discrete Mathematics and Data Analysis (англ.) / Andrew M. Gleason. — Evanston, Illinois: McDougal Littell[англ.], 1997. — ISBN 0-395-77114-5.
- ↑ Friendly, Michael Milestones in the History of Thematic Cartography, Statistical Graphics, and Data Visualization. Дата обращения: 10 сентября 2006. Архивировано из оригинала 26 апреля 2001 года.
- ↑ T. Koetsier, L. Bergmans (2005), Mathematics and the Divine, Elsevier, p. 169, ISBN 0444503285
- ↑ David A. King (1996), «Astronomy and Islamic society: Qibla, gnomics and timekeeping», in Roshdi Rashed (ed.), Encyclopedia of the History of Arabic Science, Vol. 1, pp. 128—184 [153], Routledge, London and New York
- ↑ 1 2 Coolidge, Julian[англ.]. The Origin of Polar Coordinates (англ.) // American Mathematical Monthly : journal. — 1952. — Vol. 59. — P. 78—85. — doi:10.2307/2307104. Архивировано 1 июня 2006 года.
- ↑ Boyer, C. B. Newton as an Originator of Polar Coordinates (англ.) // American Mathematical Monthly : journal. — 1949. — Vol. 56. — P. 73—78. — doi:10.2307/2306162.
- ↑ Miller, Jeff Earliest Known Uses of Some of the Words of Mathematics. Дата обращения: 10 сентября 2006. Архивировано 15 февраля 2012 года.
- ↑ Smith, David Eugene. History of Mathematics, Vol II (неопр.). — Boston: Ginn and Co., 1925. — С. 324.
- ↑ Polar Coordinates and Graphing (PDF) (13 апреля 2006). Дата обращения: 22 сентября 2006. Архивировано из оригинала 15 февраля 2012 года.
- ↑ Lee, Theodore; David Cohen, David Sklar. Precalculus: With Unit-Circle Trigonometry (англ.). — Fourth Edition. — Thomson Brooks/Cole, 2005. — ISBN 0534402305.
- ↑ Stewart, Ian; David Tall. Complex Analysis (the Hitchhiker's Guide to the Plane) (англ.). — Cambridge University Press, 1983. — ISBN 0521287634.
- ↑ Serway, Raymond A.; Jewett, Jr., John W. Principles of Physics (неопр.). — Brooks/Cole—Thomson Learning, 2005. — ISBN 0-534-49143-X.
- ↑ Torrence, Bruce Follett; Eve Torrence. The Student's Introduction to Mathematica® (англ.). — Cambridge University Press, 1999. — ISBN 0521594618.
- ↑ Claeys, Johan Polar coordinates. Дата обращения: 25 мая 2006. Архивировано из оригинала 15 февраля 2012 года.
- ↑ Smith, Julius O. Euler's Identity // Mathematics of the Discrete Fourier Transform (DFT) (англ.). — W3K Publishing, 2003. — ISBN 0-9745607-0-7.
- ↑ Husch, Lawrence S. Areas Bounded by Polar Curves. Дата обращения: 25 ноября 2006. Архивировано из оригинала 11 октября 2014 года.
- ↑ Lawrence S. Husch. Tangent Lines to Polar Graphs. Дата обращения: 25 ноября 2006. Архивировано из оригинала 2 июля 2015 года.
- ↑ Wattenberg, Frank Spherical Coordinates (1997). Дата обращения: 16 сентября 2006. Архивировано из оригинала 15 февраля 2012 года.
- ↑ Santhi, Sumrit Aircraft Navigation System. Дата обращения: 26 ноября 2006. Архивировано из оригинала 15 февраля 2012 года.
- ↑ Emergency Procedures (PDF). Дата обращения: 15 января 2007. Архивировано 15 февраля 2012 года.
Литература[править | править код]
- Гельфанд И. М., Глаголева Е. Г., Кириллов А. А. Метод координат. (недоступная ссылка) Издание пятое, стереотипное. Серия: Библиотечка физико-математической школы. Математика. Выпуск 1. М.: Наука, 1973, стр. 47-50.
Ссылки[править | править код]
- Программы для рисования графиков в каталоге ссылок Curlie (dmoz)
















![{\displaystyle (-180^{\circ },\;180^{\circ }]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/535196b36d3271ec1d81408cf666971e69c412a8)

![{\displaystyle (-\pi ,\;\pi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68d42d585d0cc7e452cd100efa4127cc28bedceb)





































































![{\displaystyle {\frac {1}{2}}\int \limits _{a}^{b}[r(\varphi )]^{2}\,d\varphi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/266e820a4d162bf3999f98de23e8237ad757c5ee)

![{\displaystyle [a,\;b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e682a8a7d3222e237401e57d673fd362523662cd)










![{\displaystyle \lim _{\Delta \varphi \to 0}\sum _{i=1}^{\infty }{\frac {1}{2}}r(\varphi _{i})^{2}\,\Delta \varphi ={\frac {1}{2}}\int \limits _{a}^{b}[r(\varphi )]^{2}\,d\varphi .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9889d1586d04c6f806776f20f2e9e4f0407d694c)




































