Распределение Бернулли Функция вероятности Функция распределения
Параметры
p
∈
(
0
,
1
)
{\displaystyle p\in (0,1)}
q
≡
1
−
p
{\displaystyle q\equiv 1-p}
Носитель
k
=
{
0
,
1
}
{\displaystyle k=\{0,1\}}
Функция вероятности
q
k
=
0
p
k
=
1
{\displaystyle {\begin{matrix}q&k=0\\p~~&k=1\end{matrix}}}
Функция распределения
0
k
<
0
q
0
≤
k
<
1
1
k
≥
1
{\displaystyle {\begin{matrix}0&k<0\\q&0\leq k<1\\1&k\geq 1\end{matrix}}}
Математическое ожидание
p
{\displaystyle p}
Мода
{
0
,
q
>
p
0
,
1
,
q
=
p
1
,
q
<
p
{\displaystyle {\begin{cases}0,&q>p\\0,1,&q=p\\1,&q<p\end{cases}}}
Дисперсия
p
q
{\displaystyle pq}
Коэффициент асимметрии
q
−
p
p
q
{\displaystyle {\frac {q-p}{\sqrt {pq}}}}
Коэффициент эксцесса
6
p
2
−
6
p
+
1
p
(
1
−
p
)
{\displaystyle {\frac {6p^{2}-6p+1}{p(1-p)}}}
Дифференциальная энтропия
−
q
ln
q
−
p
ln
p
{\displaystyle -q\ln q-p\ln p}
Производящая функция моментов
q
+
p
e
t
{\displaystyle q+pe^{t}}
Характеристическая функция
q
+
p
e
i
t
{\displaystyle q+pe^{it}}
Распределе́ние Берну́лли в теории вероятностей и математической статистике — дискретное распределение вероятностей , моделирующее случайный эксперимент произвольной природы, при заранее известной вероятности успеха или неудачи.
Случайная величина
X
{\displaystyle X}
1
{\displaystyle 1}
0
{\displaystyle 0}
p
{\displaystyle p}
q
≡
1
−
p
{\displaystyle q\equiv 1-p}
P
(
X
=
1
)
=
p
{\displaystyle \mathbb {P} (X=1)=p}
P
(
X
=
0
)
=
q
{\displaystyle \mathbb {P} (X=0)=q}
Принято говорить, что событие
{
X
=
1
}
{\displaystyle \{X=1\}}
{
X
=
0
}
{\displaystyle \{X=0\}}
Предельное свойство описывается теоремой Пуассона :
Пусть есть последовательность серий испытаний Бернулли, где
p
n
{\displaystyle p_{n}}
μ
n
{\displaystyle \mu _{n}}
Тогда если
lim
n
→
∞
p
n
=
0
;
{\displaystyle \lim _{n\to \infty }p_{n}=0;}
lim
n
→
∞
n
p
n
=
λ
;
{\displaystyle \lim _{n\to \infty }np_{n}=\lambda ;}
λ
>
0
,
{\displaystyle \lambda >0,}
то
lim
n
→
∞
P
(
ω
:
μ
n
(
ω
)
=
m
)
=
e
−
λ
λ
m
m
!
.
{\displaystyle \lim _{n\to \infty }P(\omega :\mu _{n}(\omega )=m)=e^{-\lambda }{\cfrac {\lambda ^{m}}{m!}}.}
E
[
X
]
=
p
{\displaystyle \mathbb {E} [X]=p}
D
[
X
]
=
p
(
1
−
p
)
=
p
q
{\displaystyle \operatorname {D} [X]=p(1-p)=pq}
E
X
2
−
(
E
X
)
2
=
p
−
p
2
=
p
⋅
(
1
−
p
)
=
p
q
{\displaystyle \operatorname {E} X^{2}-\left(\operatorname {E} X\right)^{2}=p-p^{2}=p\cdot (1-p)=pq}
Вообще, легко видеть, что
E
[
X
n
]
=
Pr
(
X
=
1
)
⋅
1
n
+
Pr
(
X
=
0
)
⋅
0
n
=
p
⋅
1
n
+
q
⋅
0
n
=
p
=
E
[
X
]
,
∀
n
∈
N
{\displaystyle \mathbb {E} \left[X^{n}\right]=\Pr(X=1)\cdot 1^{n}+\Pr(X=0)\cdot 0^{n}=p\cdot 1^{n}+q\cdot 0^{n}=p=\mathbb {E} [X],\forall n\in \mathbb {N} }
Если независимые случайные величины
X
1
,
…
,
X
n
{\displaystyle X_{1},\ldots ,X_{n}}
p
{\displaystyle p}
Y
=
∑
i
=
1
n
X
i
{\displaystyle Y=\sum \limits _{i=1}^{n}X_{i}}
имеет биномиальное распределение с
n
{\displaystyle n}
Hazewinkel, Michiel, ed. (2001), "Binomial distribution", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 Дискретные Абсолютно
 Функция вероятности
Функция вероятности 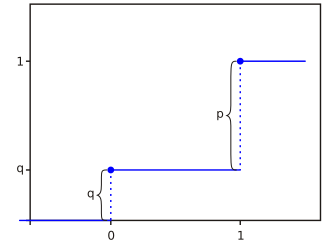 Функция распределения
Функция распределения 

























![{\displaystyle \mathbb {E} [X]=p}](https://wikimedia.org/api/rest_v1/media/math/render/svg/41bff53623cf28729d4da4500f0618fd24380b0b)
![{\displaystyle \operatorname {D} [X]=p(1-p)=pq}](https://wikimedia.org/api/rest_v1/media/math/render/svg/676350236a16d3c5d5d603eaf93da7b006fc3454)

![{\displaystyle \mathbb {E} \left[X^{n}\right]=\Pr(X=1)\cdot 1^{n}+\Pr(X=0)\cdot 0^{n}=p\cdot 1^{n}+q\cdot 0^{n}=p=\mathbb {E} [X],\forall n\in \mathbb {N} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9798a45d24eee884b4c9b48c1b79129d8132b4fc)


