Знакочередующийся ряд натуральных чисел

Первые 15000 частичных сумм ряда 0 + 1 − 2 + 3 − 4 + …

Знакочередующийся ряд натуральных чисел — знакочередующийся ряд, слагаемые которого по модулю представляют собой последовательные натуральные числа и имеют чередующийся знак: 1 − 2 + 3 − 4 + …. Частичная сумма с номером m этого ряда описывается выражением:

$\sum _{n=1}^{m}n(-1)^{n-1}$.

Такой числовой ряд расходится, то есть частичные суммы ряда не стремятся ни к какому конечному пределу. Тем не менее, в середине XVIII века Леонард Эйлер предложил выражение, которое он охарактеризовал как «парадоксальное»:

$1-2+3-4+\cdots ={\frac {1}{4}}.$

Математический аппарат, позволяющий интерпретировать это выражение, был разработан гораздо позже. Начиная с 1890 года Чезаро, Борель и другие математики строго сформулировали методы получения обобщённых сумм расходящихся рядов, а также дополнили идеи Эйлера новыми интерпретациями. Многие из этих методов для суммы ряда дают результат, равный 1⁄4. Суммирование по Чезаро является одним из немногих методов, который не позволяет определить сумму 1 − 2 + 3 − 4 + ... Таким образом, чтобы получить конечную сумму обобщенным методом суммирования для этого ряда, требуется иной подход, например применение суммирования методом Абеля.

Знакочередующийся натуральный ряд тесно связан с рядом Гранди (1 − 1 + 1 − 1 + …). Эйлер трактовал эти ряды как два частных случая ряда 1 − 2ⁿ + 3ⁿ − 4ⁿ + …, который он изучал для произвольного n, работая над Базельской проблемой, и получил функциональные уравнения для функций, известных ныне как эта-функция Дирихле и дзета-функция Римана.

Расходимость

Члены последовательности (1, −2, 3, −4, …) не стремятся к нулю, поэтому согласно необходимому условию сходимости ряд расходится:

1 = 1,

1 − 2 = −1,

1 − 2 + 3 = 2,

1 − 2 + 3 − 4 = −2,

1 − 2 + 3 − 4 + 5 = 3,

1 − 2 + 3 − 4 + 5 − 6 = −3,

…

$\sum _{n=1}^{m}(-1)^{n-1}n\;\;={\frac {(-1)^{m-1}(2m+1)+1}{4}}$

Эта последовательность примечательна тем, что в ней присутствует каждое целое число — даже ноль, если учитывать пустую частичную сумму — и таким образом множество значений членов этой последовательности счётно. Эта последовательность частичных сумм показывает, что ряд не сходится ни к какому конкретному числу (для любого x можно найти член, после которого все последующие частичные суммы будут находиться вне интервала $[x-1,x+1]$), и поэтому знакочередующийся натуральный ряд расходится.

Эвристика для суммирования

Стабильность и линейность

Поскольку члены 1, −2, 3, −4, 5, −6, … подчиняются простой закономерности, знакочередующийся натуральный ряд можно преобразовать сдвигом и почленным сложением с целью приписать ему некоторое числовое значение. Если выражение s = 1 − 2 + 3 − 4 + … для какого-то обычного числа s имеет смысл, то следующее формальное преобразование позволяет утверждать, что его значение в некотором смысле равно s = 1⁄4:.

${\begin{array}{rclllll}4s&=&&(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )&{}+(1-2+3-4+\cdots )\\&=&&(1-2+3-4+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}+1+(-2+3-4+5+\cdots )&{}-1+(3-4+5-6\cdots )\\&=&1+[&(1-2-2+3)&{}+(-2+3+3-4)&{}+(3-4-4+5)&{}+(-4+5+5-6)+\cdots ]\\&=&1+[&0+0+0+0+\cdots ]\\4s&=&1\end{array}}$

При сложении четырёх копий 1 − 2 + 3 − 4 + …,, используя только сдвиги и почленное сложение, единица.

Поэтому $s={\frac {1}{4}}$. Справа этот вывод проиллюстрирован графически.

Несмотря на то, что знакочередующийся натуральный ряд расходится и не имеет суммы в обычном смысле, выражение s = 1 − 2 + 3 − 4 + … = 1⁄4 даёт естественный ответ, если такая сумма может быть определена. Обобщённое определение «суммы» расходящегося ряда называется методом суммирования, который позволяет находить суммы для некоторого подмножества всех последовательностей. Существует множество методов обобщенного суммирования рядов (некоторые из них описаны ниже), которые обладают некоторыми свойствами обычного суммирования рядов. Выше было доказано следующее: если применить любой метод обобщенного суммирования, являющийся линейным и стабильным, который позволит получить сумму ряда 1 − 2 + 3 − 4 + …, то эта сумма составит 1⁄4. Более того, поскольку:

${\begin{array}{rcllll}2s&=&&(1-2+3-4+\cdots )&+&(1-2+3-4+\cdots )\\&=&1+&(-2+3-4+\cdots )&{}+1-2&+(3-4+5\cdots )\\&=&0+&(-2+3)+(3-4)+(-4+5)+\cdots \\2s&=&&1-1+1-1\cdots \end{array}}$

такой метод даст и сумму для ряда Гранди, которая будет равна 1 − 1 + 1 − 1 + … = 1⁄2.

Произведение Коши

В 1891 году Эрнесто Чезаро выразил надежду, что анализ расходящихся рядов выльется в самостоятельное исчисление, указывая: «Уже пишут

${(1-1+1-1+\dots )}^{2}=1-2+3-4+\ldots$

и утверждают, что обе стороны равны $1/4$.». Для Чезаро это выражение было применением теоремы, опубликованной им годом ранее, и которую можно считать первой теоремой в истории суммируемых расходящихся рядов. Детали этого метода суммирования изложены ниже; основная идея состоит в том, что $1-2+3-4+\ldots$ является произведением Коши $1-1+1-1+\ldots$ на $1-1+1-1+\ldots$.

Произведение Коши для двух бесконечных последовательностей определено, даже если они обе расходятся. В случае, когда

$\sum {a_{n}}=\sum {b_{n}}=\sum {{(-1)}^{n}},$

члены произведения Коши получаются из конечной диагональной суммы:

${\begin{array}{rcl}c_{n}&=&\displaystyle \sum _{k=0}^{n}a_{k}b_{n-k}=\sum _{k=0}^{n}(-1)^{k}(-1)^{n-k}\\[1em]&=&\displaystyle \sum _{k=0}^{n}(-1)^{n}=(-1)^{n}(n+1).\end{array}}$

И тогда результирующая последовательность: $\sum _{n=0}^{\infty }(-1)^{n}(n+1)=1-2+3-4+\ldots .$

Поэтому метод суммирования, который сохраняет произведение Коши, и даёт сумму

$1-1+1-1+\ldots ={\frac {1}{2}},$

также даст сумму

$1-2+3-4+\ldots ={\frac {1}{4}}.$

С использованием результатов, полученных в предыдущей секции, из этого вытекает эквивалентность суммируемости $1-1+1-1+\ldots$ и $1-2+3-4+\ldots$ при использовании методов суммирования, являющихся линейными, стабильными и сохраняющих произведение Коши.

Теорема Чезаро — это только пример. Ряд

$1-1+1-1+\ldots$

является суммируемым по Чезаро в слабом смысле, и называется $(C,\;1)$-суммируемым, в то время как

$1-2+3-4+\ldots$

требует более сильной формы теоремы Чезаро и называется $(C,2)$-суммируемым. Поскольку все формы метода суммирования по Чезаро являются линейными и стабильными, значения сумм соответствуют вычисленным выше.

Частные методы

Метод Чезаро и Гёльдера

Data about the (H, 2) sum of 1⁄4

Чтобы найти сумму по Чезаро (C, 1) для 1 − 2 + 3 − 4 + …, если она существует, нужно вычислить среднее арифметическое частичных сумм ряда. Частичные суммы таковы:

1, −1, 2, −2, 3, −3, …,

и их среднее арифметическое составляет:

1, 0, 2⁄3, 0, 3⁄5, 0, 4⁄7, ….

Последовательность не сходится, поэтому 1 − 2 + 3 − 4 + … не является суммируемой по Чезаро.

Есть два широко известных обобщения суммирования методом Чезаро: концептуально более простое среди них является последовательностью методов (H, n) для натуральных чисел n, где сумма (H, 1) — это сумма по Чезаро, а высшие методы получаются многократным применением метода суммирования по Чезаро. В примере выше, чётные средние сходятся к 1⁄2, в то время как нечётные равны нулю, поэтому среднее арифметическое средних арифметических сходится к среднему между нулём и 1⁄2, что составляет1⁄4 Поэтому 1 − 2 + 3 − 4 + … является (H, 2), дающим сумму 1⁄4.

«H» — это сокращение от фамилии Отто Гёльдера, который в 1882 году доказал первым то, что сейчас математики расценивают как связь между суммированием методом Абеля и суммированием(H, n); ряд 1 − 2 + 3 − 4 + … использовался им в качестве первого примера. Тот факт, что 1⁄4 является суммой (H, 2) последовательности 1 − 2 + 3 − 4 + … гарантирует, что это также и абелева сумма; это будет непосредственно доказано ниже.

Другое часто формулируемое обобщение суммирования методом Чезаро — это последовательность методов (C, n). Было доказано, что суммирование (C, n) и (H, n) дают одинаковые результаты, но имеют разную историю. В 1887 году Чезаро близко подошёл к тому, чтобы дать определение суммированию (C, n), но ограничился приведением нескольких примеров. В частности, он получил сумму 1⁄4 для 1 − 2 + 3 − 4 + …, методом, который может быть переформулирован как (C, n), но не воспринимался таковым в своё время. Он формально определил методы (C, n) в 1890 году, для формулирования своей теоремы, гласящей что произведение Коши (C, n)-суммируемого и (C, m)-суммируемого рядов являются (C, m + n + 1)-суммируемыми.

Суммирование по Абелю

Некоторые значения 1−2x+3x²+…; 1/(1 + x)²; и пределы при стремлении к единице

В отчёте 1749 года Эйлер признавал, что ряд расходится, но всё равно планировал найти его сумму:

…когда было сказано, что сумма ряда 1−2+3−4+5−6 и т. д. составляет 1⁄4, это должно было показаться парадоксальным. Складывая 100 членов этого ряда, мы получаем −50, однако сумма 101 члена даёт +51, что очень сильно отличается от 1⁄4 и отличается ещё сильнее с увеличением числа членов. Но я уже раньше замечал, что необходимо дать слову sum более широкое значение….

Эйлер предлагал обобщение понятия «сумма ряда» несколько раз. В случае для 1 − 2 + 3 − 4 + …, его идеи похожи на то, что сейчас называется методом суммирования Абеля:

…более нет сомнений, что сумма ряда 1−2+3−4+5 + и т. д. — 1⁄4; поскольку это вытекает из раскрытия формулы 1⁄(1+1)², значение которой, несомненно, 1⁄4. Идея становится понятнее при рассмотрении обобщённого ряда 1 − 2x + 3x² − 4x³ + 5x⁴ − 6x⁵ + &c. возникающего при раскрытии выражения 1⁄(1+x)², которому этот ряд будет эквивалентен после того как мы присвоим x = 1.

Есть много способов увидеть, что как минимум для абсолютных значений |x| < 1, Эйлер прав в том, что

$1-2x+3x^{2}-4x^{3}+\cdots ={\frac {1}{(1+x)^{2}}}.$

Можно раскрыть правую часть по Тейлору, либо применить формальный процесс деления многочленов столбиком. Начиная с левой части, можно использовать общую эвристику, приведённую выше, и перемножить (1+x) на себя, или возвести в квадрат ряд 1 − x + x² − …. Эйлер, по-видимому, также предложил почленно продифференцировать этот ряд.

С современной точки зрения, последовательность 1 − 2x + 3x² − 4x³ + … не определяет функцию в точке x = 1, поэтому это значение не может быть просто подставлено в результирующее выражение. Поскольку функция определена для всех |x| < 1, можно вычислять предел при стремлении x к единице, и это будет определением абелевой суммы:

$\lim _{x\rightarrow 1-0}\sum _{n=1}^{\infty }n(-x)^{n-1}=\lim _{x\rightarrow 1-0}{\frac {1}{(1+x)^{2}}}={\frac {1}{4}}.$

Эйлер и Борель

Суммирование по Эйлеру 1⁄2 − 1⁄4

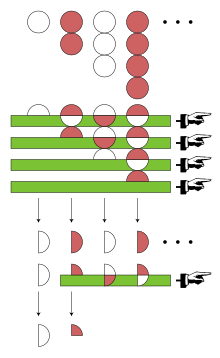
Эйлер применил к последовательностям другой подход: преобразование Эйлера, одно из своих изобретений. Чтобы вычислить преобразование Эйлера, начинают с последовательности положительных членов — в данном случае 1, 2, 3, 4, …. Первый член этой последовательности обозначен a₀.

Далее нужно получить последовательность конечных разностей среди 1, 2, 3, 4, …; это просто 1, 1, 1, 1, …. Первый элемент этой новой последовательности обозначается Δa₀. Преобразование Эйлера также зависит от разности разностей и более высоких итераций, но все разности среди 1, 1, 1, 1, ... равны 0. В таком случае преобразование Эйлера для 1 − 2 + 3 − 4 + … определяется следующим образом:

${\frac {1}{2}}a_{0}-{\frac {1}{4}}\Delta a_{0}+{\frac {1}{8}}\Delta ^{2}a_{0}-\cdots ={\frac {1}{2}}-{\frac {1}{4}}.$

В современной терминологии, 1 − 2 + 3 − 4 + … называется суммируемым по Эйлеру, с суммой равной 1⁄4.

Суммируемость по Эйлеру также предполагает ещё один вид суммируемости. Представляя 1 − 2 + 3 − 4 + … как

$\sum _{k=0}^{\infty }a_{k}=\sum _{k=0}^{\infty }(-1)^{k}(k+1),$

получается сходящийся в каждой точке ряд:

$a(x)=\sum _{k=0}^{\infty }{\frac {(-1)^{k}(k+1)x^{k}}{k!}}=e^{-x}(1-x).$

Таким образом, борелева сумма ряда 1 − 2 + 3 − 4 + … составляет:

$\int _{0}^{\infty }e^{-x}a(x)\,dx=\int _{0}^{\infty }e^{-2x}(1-x)\,dx={\frac {1}{2}}-{\frac {1}{4}}.$

Разделение шкал

Саичев и Войчыньский пришли к значению 1 − 2 + 3 − 4 + … = 1⁄4, применяя два физических принципа: отбрасывание бесконечно малых и разделение шкал. Точнее, эти принципы помогли им сформулировать широкое семейство «методов φ-суммирования», все из которых дают сумму 1⁄4:

• Если φ(x) — это функция, первая и вторая производная которой непрерывно интегрируема на (0, ∞), такая что φ(0) = 1 и пределы φ(x) и xφ(x) при стремлении к +∞ оба равны нулю, то:

$\lim _{\delta \rightarrow 0}\sum _{m=0}^{\infty }(-1)^{m}(m+1)\varphi (\delta m)={\frac {1}{4}}.$

Этот результат является обобщением абелева суммирования которое получается заменой φ(x) = exp(−x). Общее утверждение может быть доказано при помощи группирования по парам членов ряда по m и преобразовывая выражение в интеграл Римана. Относительно последнего шага, в соответствующем доказательстве для 1 − 1 + 1 − 1 + … применяется теорема Лагранжа о среднем значении, но здесь требуется более сильная форма Лагранжа теоремы Тейлора.

Обобщения ряда

Выдержки из стр.233 работы E212 — Institutiones calculi differentialis cum eius usu in analysi finitorum ac doctrina serierum. Эйлер суммирует ряды подобного типа, около 1755.

Трёхкратное произведение Коши для ряда 1 − 1 + 1 − 1 + … даёт ряд 1 − 3 + 6 − 10 + …, — знакочередующийся ряд из треугольных чисел, его абелева и эйлерова суммы равны 1⁄8. Четырёхкратное произведение Коши ряда 1 − 1 + 1 − 1 + … даёт ряд 1 − 4 + 10 − 20 + …, — знакочередующийся ряд из тетраэдральных чисел, абелева сумма которого равна 1⁄16.

Другое обобщение ряда 1 − 2 + 3 − 4 + … возможно в несколько другом направлении: это семейство рядов 1 − 2ⁿ + 3ⁿ − 4ⁿ + … для других значений n. При положительных n подобный ряд имеет следующую абелеву сумму:

$1-2^{n}+3^{n}-\cdots ={\frac {2^{n+1}-1}{n+1}}B_{n+1}$

где B_n — числа Бернулли. Для чётных n это сводится к

$1-2^{2k}+3^{2k}-\cdots =0.$

Последняя сумма стала объектом насмешек со стороны Нильса Абеля в 1826:

«Расходящиеся ряды — это всецело работа дьявола, и стыд тому, кто пытается найти какие-либо доказательства относительно них. Можно получить из них, что захочешь, и это они породили так много горя и парадоксов. Можно ли представить что-либо более ужасное, чем сказать, что

0 = 1 − 2ⁿ + 3ⁿ − 4ⁿ + и т. д.

где n — положительное число. Здесь есть над чем посмеяться, друзья.»

Учитель Чезаро, Эжен Каталан, также пренебрежительно относился к расходящимся рядам. Под влиянием Каталана Чезаро изначально характеризовал «условные формулы» для ряда 1 − 2ⁿ + 3ⁿ − 4ⁿ + ... как «абсурдные выражения», и в 1883 Чезаро выражал общепринятый взгляд, что эти формулы ошибочны, но могут в чём-то быть формально полезны. Наконец, в своей работе Sur la multiplication des séries 1890 года Чезаро пришёл к современному подходу, начиная с определений.

Ряды были также исследованы для нецелых значений n; они дают эта-функцию Дирихле. Отчасти мотивацией Эйлера к изучению рядов, связанных с рядом 1 − 2 + 3 − 4 + …, стало функциональное уравнение для эта-функции, которое непосредственно ведёт к функциональному уравнению для дзета-функции Римана. Эйлер уже был знаменит нахождением значений этих функций для положительных чётных целых чисел (включая решение базельской проблемы), и попытался найти значения и для положительных нечётных целых чисел (включая постоянную Апери) — эта проблема не разрешена по сей день. Работать методами Эйлера с эта-функцией несколько проще, потому что её ряды Дирихле везде суммируемы по Абелю; ряды Дирихле дзета-функции гораздо сложнее суммировать там, где они расходятся. К примеру, 1 − 2 + 3 − 4 + … в дзета-функции соответствует знакопостоянный ряд 1 + 2 + 3 + 4 + …, который используется в современной физике, но требует гораздо более сильных методов суммирования.