Фигурные числа

Фигурные числа — числа, которые можно представить с помощью геометрических фигур. Это историческое понятие восходит к пифагорейцам, которые развивали алгебру на геометрической основе и представляли любое положительное целое число в виде набора точек на плоскости[1]. Отголоском этого подхода остались выражения «возвести число в квадрат» или «в куб»[2].
Традиционно различают два основных класса фигурных чисел[3]:
- плоские многоугольные числа — числа, связанные с определённым многоугольником. Они делятся на классические и центрированные;
- пространственные многогранные числа — числа, связанные с определённым многогранником.
В свою очередь, каждый класс фигурных чисел делится на разновидности, каждая из которых связана с определённой геометрической фигурой: треугольником, квадратом, тетраэдром и т. д.
Существуют также обобщения фигурных чисел на многомерные пространства. В древности, когда арифметика не отделялась от геометрии, рассматривались ещё несколько видов фигурных чисел, в настоящее время не используемых.
В теории чисел и комбинаторике фигурные числа связаны с многими другими классами целых чисел — биномиальными коэффициентами, совершенными числами, числами Мерсенна, Ферма, Фибоначчи, Люка и другими[4].
Классические многоугольные числа[править | править код]
Для краткости в этом разделе классические многоугольные числа называются просто «многоугольными числами».
Геометрическое определение[править | править код]

Многоугольные числа — это последовательность, указывающая число точек, построенную согласно правилам, которые проиллюстрируем на примере семиугольника. Ряд семиугольных чисел начинается с 1 (базовая точка), затем следует 7, потому что 7 точек образуют правильный семиугольник, 6 точек добавились. Третье число соответствует семиугольнику, у которого стороны содержат уже не по две, а по три точки, причём все точки, построенные на предыдущих шагах, также учитываются. Из рисунка видно, что третья фигура содержит 18 точек, прибавка (Пифагор называл её «гномон») составила 11 точек. Нетрудно видеть, что прибавки образуют арифметическую прогрессию, в которой каждый член на 5 больше, чем предыдущий[5].
Переходя к общему -угольнику, можно заключить, что на каждом шаге число точек, соответствующее фигурному числу, увеличивается как сумма арифметической прогрессии[5] с первым членом 1 и разностью
Алгебраическое определение[править | править код]
Общее определение k-угольного числа для любого следует из представленного выше геометрического построения. Его можно сформулировать следующим образом[6]:
|
-е по порядку k-угольное число есть сумма первых членов арифметической прогрессии, у которой первый член равен 1, а разность равна |
Например, треугольные числа получаются как частичные суммы ряда , а четырёхугольным (квадратным) числам соответствует ряд
Последовательность k-угольных чисел имеет вид[7]:
Общую формулу для явного подсчёта -го по порядку k-угольного числа можно получить, представив его как сумму арифметической прогрессии[8]:
| . | (ОКФ) |
В некоторых источниках последовательность фигурных чисел начинают с нуля (например, в A000217):
В этом случае в общей формуле для допускается В данной статье фигурные числа нумеруются начиная с единицы, а расширенный ряд оговаривается особо.
Существует также рекуррентная формула для вычисления многоугольного числа[8]:
- .
При увеличении числа сторон на единицу соответствующие фигурные числа изменяются согласно формуле Никомаха[9]:
| , где . | (Никомах) |
Поскольку линейно зависит от справедлива формула:
- , где .
Другими словами, каждое многоугольное число есть среднее арифметическое для равноотстоящих от него по многоугольных чисел с тем же номером.
Если — простое число, то второе -угольное число, равное , также простое; это единственная ситуация, когда многоугольное число является простым, к чему можно прийти, записав общую формулу в следующем виде:
- .
Доказательство: пусть Если чётно, то фигурное число делится на , а если нечётно, то делится на . В обоих случаях фигурное число оказывается составным[10].
Ряды из обратных многоугольных чисел
сходятся. Их сумма может быть представлена в виде где — постоянная Эйлера — Маскерони, — дигамма-функция[11].
Исторический очерк[править | править код]
Фигурные числа, по мнению пифагорейцев, играют важную роль в структуре мироздания. Поэтому их изучением занимались многие видные математики античности: Эратосфен, Гипсикл, Диофант Александрийский, Теон Смирнский и другие. Гипсикл (II век до н. э.) дал общее определение -угольного числа как суммы членов арифметической прогрессии, у которой первый член есть , а разность равна . Диофант написал большое исследование «О многоугольных числах» (III век н. э.), фрагменты которого дошли до наших дней. Определение Гипсикла приводится в книге Диофанта в следующем виде[12][13]:
Если взять сколько-нибудь чисел, начиная с единицы, имеющих одинаковые разности, то сумма их, если разность единица, будет треугольником, если же двойка, то четырёхугольником, а если тройка — пятиугольником. Количество углов определяется разностью, увеличенной на двойку, а сторона — количеством взятых чисел, считая и единицу.
О фигурных числах много говорится в пифагорейских учебниках арифметики, созданных Никомахом Геразским и Теоном Смирнским (II век), которые установили ряд зависимостей между фигурными числами разных размерностей. Большой интерес к фигурным числам проявили индийские математики и первые математики средневековой Европы (Фибоначчи, Пачоли, Кардано и др.)[14][4].
В Новое время многоугольными числами занимались Ферма, Валлис, Эйлер, Лагранж, Гаусс и другие. В сентябре 1636 года[15] Ферма сформулировал в письме Мерсенну теорему, которая сегодня называется теоремой Ферма о многоугольных числах[14]:
Я первым открыл очень красивую и совершенно общую теорему о том, что каждое число является либо треугольным, либо суммой двух или трёх треугольных чисел; каждое число или квадратное, или является суммой двух, трёх или четырёх квадратов; или пятиугольное, или является суммой двух, трёх, четырёх или пяти пятиугольных чисел, и т. д. до бесконечности, будь то для шестиугольных, семиугольных или любых многоугольных чисел. Я не могу дать здесь доказательство, которое зависит от многочисленных и запутанных тайн чисел, ибо я намерен посвятить этой теме целую книгу и получить в этой части арифметики удивительные достижения по сравнению с ранее известными пределами.
Вопреки обещанию, Ферма так и не опубликовал доказательство этой теоремы, которую в письме Паскалю (1654) назвал своим главным достижением в математике[15]. Проблемой занимались многие выдающиеся математики — в 1770 году Лагранж доказал теорему для квадратных чисел (теорема Лагранжа о сумме четырёх квадратов), в 1796 году Гаусс дал доказательство для треугольных. Полное доказательство теоремы сумел дать Коши в 1813 году[16][17].
Разновидности классических многоугольных чисел[править | править код]
Треугольные числа[править | править код]
Последовательность треугольных чисел:
- 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210 …, … (последовательность A000217 в OEIS)
Свойства[18]:
Чётность элемента последовательности меняется с периодом 4: нечётное, нечётное, чётное, чётное. Никакое треугольное число не может (в десятичной записи) оканчиваться цифрами 2, 4, 7, 9[19].
Обозначим для краткости -е треугольное число: Тогда справедливы рекуррентные формулы:
- ;
- .
Формула Баше де Мезириака: общую формулу многоугольного числа можно преобразовать так, что она покажет выражение любого многоугольного числа через треугольные:
| . | (Баше) |

Сумма двух последовательных треугольных чисел даёт полный квадрат (квадратное число):
- .
Из теоремы Ферма о многоугольных числах следует, что любое натуральное число представимо в виде суммы не более трёх треугольных чисел.
Сумма конечного ряда треугольных чисел вычисляется по формуле:
- .
Ряд из чисел, обратных треугольным (телескопический ряд), сходится[20]:
- .
Удвоенные треугольные числа дают последовательность (определённых ниже) прямоугольных чисел.
Натуральное число является треугольным тогда и только тогда, когда число является квадратным[21].
Известное в мистике «число зверя» (666) является 36-м треугольным. Оно является наименьшим треугольным числом, которое представимо в виде суммы квадратов треугольных чисел[22]: .
Треугольные числа образуют третью диагональную линию треугольника Паскаля.
Квадратные числа[править | править код]

|

| ||
Квадратные числа представляют собой произведение двух одинаковых натуральных чисел, то есть являются полными квадратами:
- 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400 …, … (последовательность A000290 в OEIS).
Каждое квадратное число, кроме единицы, есть сумма двух последовательных треугольных чисел[23]:
- . Примеры: и т. д.
Сумма квадратного числа с предшествующим ему по номеру треугольным числом даёт пятиугольное число:
- .
Эта теорема была впервые опубликована Никомахом («Введение в арифметику», II век)[24].
Сумма квадратов первых натуральных чисел вычисляется по формуле[25]:
- .
Ряд обратных квадратных чисел сходится[26]:
- .
Каждое натуральное число может быть представлено как сумма не более четырёх квадратов (теорема Лагранжа о сумме четырёх квадратов).
Тождество Брахмагупты — Фибоначчи: произведение суммы двух квадратных чисел на любую другую сумму двух квадратных чисел само представимо в виде суммы двух квадратных чисел.
Поскольку второе слагаемое справа может быть равно нулю, здесь следует рассматривать расширенный ряд квадратных чисел, начинающийся не с 1, а с нуля (см. A000290).
Пример:
- .
Пятиугольные числа[править | править код]
Последовательность пятиугольных чисел имеет вид:
- 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590 …, … (последовательность A000326 в OEIS).
Пятиугольные числа тесно связаны с треугольными[24]:
- .
Как уже упоминалось выше, пятиугольное число, начиная со 2-го номера, можно представить как сумму квадратного и треугольного числа:
- .
Если в формуле указать для более общую последовательность:
- .
то получатся обобщённые пятиугольные числа:
- 0, 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92, 100, 117, 126, 145, 155… (последовательность A001318 в OEIS).
Леонард Эйлер обнаружил обобщённые пятиугольные числа в следующем тождестве:
- .
Степени в правой части тождества образуют последовательность обобщённых пятиугольных чисел[27].
Шестиугольные числа[править | править код]
- 1, 6, 15, 28, 45, 66, 91, 120, 153, 190, 231, 276, 325, 378, 435, 496, 561, 630, 703, 780 …, … (последовательность A000384 в OEIS).
Последовательность шестиугольных чисел получается из последовательности треугольных чисел вычёркиванием элементов с чётными номерами[28]: .
Натуральное число является шестиугольным тогда и только тогда, когда число является натуральным.
Семиугольные числа[править | править код]
Восьмиугольные числа[править | править код]
Двенадцатиугольные числа[править | править код]
Двенадцатиугольные числа вычисляются по формуле :
- 1, 12, 33, 64, 105, 156, 217, 288, 369, 460, 561, 672, 793, 924, 1065, 1216, 1377, 1548, 1729, 1920 … (последовательность A051624 в OEIS).
В десятичной системе -ое двенадцатиугольное число заканчивается на ту же цифру, что и само число . Это следует из очевидного сравнения: откуда получаем: ■.
Определение, является ли заданное число многоугольным[править | править код]
Задача 1 (задача Диофанта): дано натуральное число . Определить, является ли оно многоугольным числом и если да, то для каких и . Диофант сформулировал эту проблему так: «выяснить, сколько раз данное число встречается среди всевозможных многоугольных чисел»[29].
Решение задачи сводится к решению «диофантова уравнения» (см. общую формулу):
- или: .
Перепишем полученное уравнение в виде: .
Знаменатели дробей справа взаимно просты; сумма или разность таких дробей может быть целым числом только если каждая дробь есть целое число[30], поэтому кратно , а кратно .
В результате алгоритм решения приобретает следующую форму[29]:
- Выписать все натуральные делители числа (включая и само ).
- Выписать все натуральные делители числа .
- Отобрать из первого набора те числа, которые на больше какого-либо числа из второго набора. Эти числа соответствуют .
- Для каждого отобранного подсчитать .
- Вычеркнуть пары , в которых .
Тогда все соответствующие оставшимся парам числа равны .
Пример[29]. Пусть .
- Делители .
- Делители .
- Отбор .
- Соответственно . Последнее значение следует отбросить.
Ответ: может быть представлено как , то есть как 2-е 105-угольное, 3-е 36-угольное, 5-е 12-угольное и 14-е 14-угольное число.
Задача 2: дано натуральное число требуется определить, является ли оно -угольным числом . В отличие от задачи 1, здесь задано.
Для решения можно использовать тождество Диофанта[31]:
Это тождество получается из приведённой выше общей формулы для и равносильно ей. Из тождества вытекает решение: если есть -угольное число, то есть для некоторого то есть некоторое квадратное число , и обратно. При этом номер находится по формуле[31]:
- .
Пример[31]. Определим, является ли число 10-угольным. Значение здесь равно поэтому ответ утвердительный. следовательно, является 20-м 10-угольным числом.
Производящая функция[править | править код]
Степенной ряд, коэффициенты которого — -угольные числа, сходится при :
- .
Выражение справа является производящей функцией для последовательности -угольных чисел[32].
Аппарат производящих функций позволяет применять в теории чисел и комбинаторике методы математического анализа. Приведённая формула также объясняет появление -угольных чисел среди коэффициентов ряда Тэйлора для различных рациональных дробей. Примеры:
- При : ;
- При : ;
- При :
и т. д.
Для некоторых классов многоугольных чисел существуют свои, специфические производящие функции. Например, для квадратных треугольных чисел производящая функция имеет следующий вид[33]:
- ; ряд сходится при .
Классические многоугольные числа из более чем одной разновидности[править | править код]
Существует бесконечное количество «многофигурных» (или «мультимногоугольных»)[34] чисел, то есть чисел, которые относятся одновременно к нескольким различным разновидностям фигурных чисел. Например, существуют треугольные числа, которые одновременно являются квадратными («квадратные треугольные числа»)[35]:
Треугольное число может также быть одновременно
- 1, 210, 40755, 7906276, 1533776805, 297544793910, 57722156241751, 11197800766105800, 2172315626468283465…;
- шестиугольным (все треугольные числа с нечётным номером);
- семиугольным (последовательность A046194 в OEIS):
- 1, 21, 11781, 203841, 113123361, 1957283461, 1086210502741, 18793835590881, 10429793134197921, 180458407386358101…
и т. д. Неизвестно, существуют ли числа, одновременно треугольные, квадратные и пятиугольные; проверка на компьютере чисел, меньших не обнаружила ни одного подобного числа, однако не доказано, что таковых не существует[34].
Квадратное число может быть одновременно
- 1, 9801, 94109401, 903638458801, 8676736387298001, 83314021887196947001, 799981229484128697805801…,
- 1, 1225, 1413721, 1631432881, 1882672131025, 2172602007770041, 2507180834294496361, 2893284510173841030625…,
- 1, 81, 5929, 2307361, 168662169, 12328771225, 4797839017609, 350709705290025, 25635978392186449…
и т. д.
Пятиугольное число может одновременно быть:
- 1, 40755, 1533776805, 57722156241751, 2172315626468283465, 81752926228785223683195, 3076689623521787481625080301…,
- 1, 4347, 16701685, 64167869935, 246532939589097, 947179489733441251, 3639063353022941697757…
и т. д.
Шестиугольное число обязательно является также треугольным; оно также может одновременно быть семиугольным (последовательность A48903 в OEIS):
- 1, 121771, 12625478965, 1309034909945503, 135723357520344181225, 14072069153115290487843091…
Возможны и другие сочетания трёх и более разновидностей фигурных чисел. Например, как доказано выше, число входит в четыре разновидности: Полный список таких сочетаний от треугольных до 16-угольных чисел — см. последовательность A062712 в OEIS.
Сводная таблица[править | править код]
| k | Разновидность фигурных чисел |
Общая формула | n | Сумма обратных значений[36] | Номер OEIS | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||||
| 3 | треугольное | 1/2(n2 + n) | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 | 55 | 2 | A000217 |
| 4 | квадратное | 1/2(2n2 − 0n) = n2 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 2/6 | A000290 |
| 5 | пятиугольное | 1/2(3n2 − n) | 1 | 5 | 12 | 22 | 35 | 51 | 70 | 92 | 117 | 145 | A000326 | |
| 6 | шестиугольное | 1/2(4n2 − 2n) | 1 | 6 | 15 | 28 | 45 | 66 | 91 | 120 | 153 | 190 | 2 ln 2 | A000384 |
| 7 | семиугольное | 1/2(5n2 − 3n) | 1 | 7 | 18 | 34 | 55 | 81 | 112 | 148 | 189 | 235 | A000566 | |
| 8 | восьмиугольное | 1/2(6n2 − 4n) | 1 | 8 | 21 | 40 | 65 | 96 | 133 | 176 | 225 | 280 | 3/4 ln 3 + √3/12 | A000567 |
| 9 | девятиугольное | 1/2(7n2 − 5n) | 1 | 9 | 24 | 46 | 75 | 111 | 154 | 204 | 261 | 325 | |
A001106 A244646 |
| 10 | десятиугольное | 1/2(8n2 − 6n) | 1 | 10 | 27 | 52 | 85 | 126 | 175 | 232 | 297 | 370 | ln 2 + /6 | A001107 |
| 11 | 11-угольное | 1/2(9n2 − 7n) | 1 | 11 | 30 | 58 | 95 | 141 | 196 | 260 | 333 | 415 | A051682 | |
| 12 | 12-угольное | 1/2(10n2 − 8n) | 1 | 12 | 33 | 64 | 105 | 156 | 217 | 288 | 369 | 460 | A051624 | |
| 13 | 13-угольное | 1/2(11n2 − 9n) | 1 | 13 | 36 | 70 | 115 | 171 | 238 | 316 | 405 | 505 | A051865 | |
| 14 | 14-угольное | 1/2(12n2 − 10n) | 1 | 14 | 39 | 76 | 125 | 186 | 259 | 344 | 441 | 550 | 2/5 ln 2 + 3/10 ln 3 + √3/10 | A051866 |
| 15 | 15-угольное | 1/2(13n2 − 11n) | 1 | 15 | 42 | 82 | 135 | 201 | 280 | 372 | 477 | 595 | A051867 | |
| 16 | 16-угольное | 1/2(14n2 − 12n) | 1 | 16 | 45 | 88 | 145 | 216 | 301 | 400 | 513 | 640 | A051868 | |
| 17 | 17-угольное | 1/2(15n2 − 13n) | 1 | 17 | 48 | 94 | 155 | 231 | 322 | 428 | 549 | 685 | A051869 | |
| 18 | 18-угольное | 1/2(16n2 − 14n) | 1 | 18 | 51 | 100 | 165 | 246 | 343 | 456 | 585 | 730 | 4/7 ln 2 − √2/14 ln (3 − 2√2) + (1 + √2)/14 | A051870 |
| 19 | 19-угольное | 1/2(17n2 − 15n) | 1 | 19 | 54 | 106 | 175 | 261 | 364 | 484 | 621 | 775 | A051871 | |
| 20 | двадцатиугольное | 1/2(18n2 − 16n) | 1 | 20 | 57 | 112 | 185 | 276 | 385 | 512 | 657 | 820 | A051872 | |
| 21 | 21-угольное | 1/2(19n2 − 17n) | 1 | 21 | 60 | 118 | 195 | 291 | 406 | 540 | 693 | 865 | A051873 | |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 1000 | 1000-угольное | 1/2(998n2 − 996n) | 1 | 1000 | 2997 | 5992 | 9985 | 14976 | 20965 | 27952 | 35937 | 44920 | A195163 | |
| 10000 | 10000-угольное | 1/2(9998n2 − 9996n) | 1 | 10000 | 29997 | 59992 | 99985 | 149976 | 209965 | 279952 | 359937 | 449920 | A167149 | |
Центрированные многоугольные числа[править | править код]
Определение[править | править код]
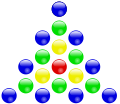
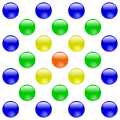
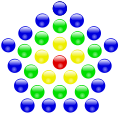
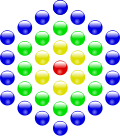
Центрированные -угольные числа () — это класс фигурных чисел, получаемый следующим геометрическим построением. Сначала на плоскости фиксируется некоторая центральная точка. Затем вокруг неё строится правильный k-угольник с точками вершин, каждая сторона содержит две точки (см. рисунок). Далее снаружи строятся новые слои -угольников, причём каждая их сторона на новом слое содержит на одну точку больше, чем в предыдущем слое, то есть начиная со второго слоя каждый следующий слой содержит на больше точек, чем предыдущий. Общее число точек внутри каждого слоя и принимается в качестве центрированного многоугольного числа (точка в центре считается начальным слоем)[37].
Примеры построения центрированных многоугольных чисел:
| Треугольные | Квадратные | Пятиугольные | Шестиугольные |
|---|---|---|---|
|
|
|
|
Из построения видно, что центрированные многоугольные числа получаются как частичные суммы следующего ряда: (например, центрированные квадратные числа, для которых образуют последовательность: ) Этот ряд можно записать как , откуда видно, что в скобках — порождающий ряд для классических треугольных чисел (см. выше). Следовательно, каждая последовательность центрированных -угольных чисел, начиная со 2-го элемента, может быть представлена как , где — последовательность треугольных чисел. Например, центрированные квадратные числа — это учетверённые треугольные числа плюс , порождающий ряд для них имеет вид: [38]
Из приведённой выше формулы для треугольных чисел можно выразить общую формулу для -го центрированного -угольного числа [38]:
| (ОЦФ) |
Производящая функция для центрированных многоугольных чисел имеет вид[39]:
- .
Разновидности центрированных многоугольных чисел[править | править код]
Центрированные треугольные числа[править | править код]

-е по порядку центрированное треугольное число задаётся формулой:
- .
Следствие (при ): .
Первые элементы последовательности центрированных треугольных чисел:
- 1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, 199, 235, 274, 316, 361, 409, 460, 514, 571 …, (последовательность A005448 в OEIS).
- Некоторые свойства[40]
- Каждое центрированное треугольное число, начиная с 10, является суммой трёх последовательных классических треугольных чисел:
- Из следствия общей формулы видно, что каждое центрированное треугольное число при делении на 3 даёт остаток 1, а частное (если оно положительно), есть классическое треугольное число .
- Некоторые центрированные треугольные числа являются простыми[10]: 19, 31, 109, 199, 409 … (последовательность A125602 в OEIS).
Центрированные квадратные числа[править | править код]
| 1 | 5 | 13 | 25 | |||
|---|---|---|---|---|---|---|
-е по порядку центрированное 4-угольное (квадратное) число задаётся формулой:
- .
Первые элементы последовательности центрированных квадратных чисел:
- 1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, 265, 313, 365, 421, 481, 545, 613, 685, 761 …, (последовательность A001844 в OEIS).
- Некоторые свойства[41]
- Как видно из общей формулы, центрированное квадратное число есть сумма двух последовательных квадратов.
- Все центрированные квадратные числа нечётны, и последняя цифра в их десятичном представлении меняется в цикле: 1-5-3-5-1.
- Все центрированные квадратные числа и их делители дают остаток 1 при делении на 4, а при делении на 6, 8 или 12 дают остаток 1 или 5.
- Все центрированные квадратные числа, за исключением 1, представляют длину гипотенузы в одной из пифагоровых троек (например, 3-4-5, 5-12-13). Таким образом, каждое центрированное квадратное число равно числу точек внутри данного расстояния в кварталах от центральной точки на квадратной решётке.
- Разность между двумя последовательными классическими восьмиугольными числами есть центрированное квадратное число.
- Некоторые центрированные квадратные числа являются простыми (как показано выше, классические квадратные числа, начиная с третьего по порядку, заведомо составные). Примеры простых центрированных квадратных чисел:
Центрированные пятиугольные числа[править | править код]

-е по порядку центрированное пятиугольное число задаётся формулой:
- .
Несколько первых центрированных пятиугольных чисел:
- 1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331, 391, 456, 526, 601, 681, 766, 856, 951 …, … (последовательность A005891 в OEIS)
Чётность центрированных пятиугольных чисел меняется по правилу: чётное-чётное-нечётное-нечётное, и последняя десятичная цифра меняется в цикле: 6-6-1-1.
Некоторые центрированные пятиугольные числа являются простыми[10]: 31, 181, 331, 391, 601 . . . (последовательность A145838 в OEIS).
Центрированные шестиугольные числа[править | править код]

-е по порядку центрированное шестиугольное число задаётся формулой:
- .
Несколько первых центрированных шестиугольных чисел:
- 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, 469, 547, 631, 721, 817, 919 … … (последовательность A003215 в OEIS).
- Некоторые свойства[42]
- Последний десятичный знак центрированных шестиугольных чисел меняется в цикле 1-7-9-7-1.
- Сумма первых n центрированных шестиугольных чисел равна «кубическому числу» .
- Справедливо рекуррентное равенство: .
- Некоторые центрированные шестиугольные числа являются простыми[10]: 7, 19, 37, 61, 127 … (последовательность A002407 в OEIS).
Центрированные семиугольные числа[править | править код]

-е по порядку центрированное семиугольное число задаётся формулой . Его можно также вычислить умножением треугольного числа на 7 с добавлением 1.
Несколько первых центрированных семиугольных чисел:
- 1, 8, 22, 43, 71, 106, 148, 197, 253, 316, 386, 463, 547, 638, 736, 841, 953 …, … (последовательность A069099 в OEIS).
Чётность центрированных семиугольных чисел меняется в цикле нечётный-чётный-чётный-нечётный.
Некоторые центрированные семиугольные числа являются простыми[10]:
Существуют также центрированные семиугольные числа, входящие в пары простых чисел-близнецов:
- 43, 71, 197, 463, 1933, 5741, 8233, 9283, 11173, 14561, 34651 … (последовательность A144975 в OEIS).
Центрированные восьмиугольные числа[править | править код]
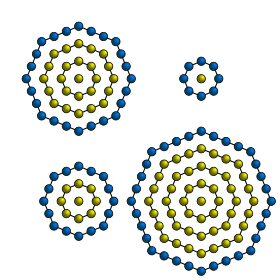
-е по порядку центрированное восьмиугольное число задаётся формулой .
Несколько первых центрированных восьмиугольных чисел:
- 1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, 625, 729, 841, 961, 1089.
- Некоторые свойства[43]
- Все центрированные восьмиугольные числа нечётны, и их последняя десятичная цифра меняется в цикле 1-9-5-9-1.
- Центрированное восьмиугольное число совпадает с классическим квадратным числом с нечётным номером: Другими словами, нечётное число является центрированным восьмиугольным числом тогда и только тогда, когда оно является квадратом целого числа.
- Из предыдущего свойства следует, что все центрированные восьмиугольные числа, кроме 1, составные.
Центрированные девятиугольные числа[править | править код]
-е по порядку центрированное девятиугольное число определяется общей формулой .
Умножая -ое треугольное число на 9 и добавляя 1, получим -ое центрированное девятиугольное число, но имеется и более простая связь с треугольными числами — каждое третье треугольное число (1-е, 4-е, 7-е и т. д.) также является центрированным девятиугольным числом, и так можно получить все центрированные девятиугольные числа. Формальная запись: .
Первые центрированные девятиугольные числа:
- 1, 10, 28, 55, 91, 136, 190, 253, 325, 406, 496, 595, 703, 820, 946 … (последовательность A060544 в OEIS).
За исключением 6, все чётные совершенные числа являются также центрированными девятиугольными числами. В 1850-м году математик-любитель Фредерик Поллок высказал предположение, которое до сих пор не доказано и не опровергнуто, что любое натуральное число есть сумма максимум одиннадцати центрированных девятиугольных чисел[44].
Из общей формулы следует, что все центрированные девятиугольные числа, кроме 1, составные.
Центрированные десятиугольные числа[править | править код]

-е по порядку центрированное десятиугольное число задаётся формулой .
Первые представители центрированных десятиугольных чисел:
- 1, 11, 31, 61, 101, 151, 211, 281, 361, 451, 551, 661, 781, 911, 1051 … (последовательность A062786 в OEIS).
Подобно другим k-угольным числам, -ое центрированное десятиугольное число можно вычислить, умножая -ое треугольное число на , в нашем случае 10, затем добавляя 1. Как следствие, центрированные десятиугольные числа могут быть получены просто добавлением 1 к десятичному представлению числа. Таким образом, все центрированные десятиугольные числа нечётны и всегда оканчиваются на 1 в десятичном представлении.
Часть центрированных десятиугольных чисел являются простыми, например:
- 11, 31, 61, 101, 151, 211, 281, 661, 911, 1051, 1201, 1361, 1531, 1901, 2311, 2531, 3001, 3251, 3511, 4651, 5281… (последовательность A090562 в OEIS).
Многоугольные числа, одновременно классические и центрированные[править | править код]
Некоторые центрированные многоугольные числа совпадают с классическими, например: ; для краткости будем называть такие многоугольные числа двойными.
- 1. Двойные числа с общим параметром (число углов): имеет место тождество[45]:
- .
- 2. Двойные треугольные числа с разными Пример: (последовательность A128862 в OEIS). Для их нахождения надо решить диофантово уравнение:
- 3. Классические квадратные, являющиеся центрированными треугольными числами. Их определяет диофантово уравнение:
- 4. Классические треугольные, являющиеся центрированными шестиугольными числами. Первые такие числа: (последовательность A006244 в OEIS). Их определяет диофантово уравнение:
- 5. Классические квадратные, являющиеся центрированными шестиугольными числами. Первые такие числа: (последовательность A006051 в OEIS). Их определяет диофантово уравнение:
Пространственные фигурные числа[править | править код]
Наряду с рассмотренными выше фигурными числами для плоских фигур, можно определить пространственные или даже многомерные их аналоги. Уже античные математики исследовали тетраэдральные и квадратные пирамидальные числа. Несложно определить числа, связанные с пирамидами, в основании которых лежит любой другой многоугольник, например:
- Пятиугольное пирамидальное число.
- Шестиугольное пирамидальное число.
- Семиугольное пирамидальное число.
Другие разновидности пространственных фигурных чисел связаны с классическими многогранниками.
Пирамидальные числа[править | править код]

Пирамидальные числа определяются следующим образом:
|
-е по порядку k-угольное пирамидальное число есть сумма первых плоских фигурных чисел с тем же числом углов :
|
Геометрически пирамидальное число можно представить как пирамиду из слоёв (см. рисунок), каждый из которых содержит от 1 (верхний слой) до (нижний) шаров.
По индукции нетрудно доказать общую формулу для пирамидального числа, известную ещё Архимеду[46]:
| . | (ОПФ) |
Правую часть этой формулы можно также выразить через плоские многоугольные числа:
- .
Существует трёхмерный аналог формулы Никомаха для пирамидальных чисел[47]:
- .
Производящая функция пирамидальных чисел имеет вид[48]:
- .
Треугольные пирамидальные (тетраэдральные) числа[править | править код]

Треугольные пирамидальные числа, называемые также тетраэдральными — это фигурные числа, которые представляют тетраэдр, то есть пирамиду, в основании которой лежит треугольник. Согласно приведенному выше общему определению пирамидальных чисел, е по порядку тетраэдральное число определяется как сумма первых треугольных чисел:
Общая формула для тетраэдрального числа: .
Несколько первых тетраэдральных чисел:
- 1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364, 455, 560, 680, 816, 969 … (последовательность A000292 в OEIS).
Интересно, что пятое число равно сумме всех предыдущих.
Существует трёхмерный аналог формулы Баше де Мезириака, а именно разложение произвольного пирамидального числа по тетраэдральным[47]:
- .
Пять тетраэдральных чисел одновременно являются треугольными (последовательность A027568 в OEIS):
- 1, 10, 120, 1540, 7140.
Только три тетраэдральных числа являются квадратными числами (последовательность A003556 в OEIS):
- , , .
Одна из «гипотез Поллока» (1850 год): каждое натуральное число представимо как сумма не более пяти тетраэдральных чисел. До сих пор не доказана, хотя проверена для всех чисел, меньших 10 миллиардов[49][50].
Квадратные пирамидальные числа[править | править код]
Квадратные пирамидальные числа часто кратко называют просто пирамидальными. Для них пирамида имеет квадратное основание. Начальная последовательность:
Общая формула для квадратного пирамидального числа: .
Квадратное пирамидальное число также выражает общее количество квадратов[51] в квадратной сетке .
Между квадратными и треугольными пирамидальными числами существует следующая зависимость[52]:
- .
Выше было отмечено, что сумма последовательных треугольных чисел есть квадратное число; аналогично сумма последовательных тетраэдральных чисел есть квадратное пирамидальное число[52]: .
Многогранные числа[править | править код]
По аналогии с квадратными можно ввести «кубические числа» а также числа, соответствующие другим правильным и неправильным многогранникам — например, платоновым телам:
Предусмотрены также их центрированные варианты.
Кубические числа[править | править код]
Кубические числа представляют собой произведение трёх одинаковых натуральных чисел и имеют общий вид Начальные значения:
Кубическое число можно выразить как разность квадратов последовательных треугольных чисел[53]:
- , .
Следствие: сумма первых кубических чисел равна квадрату -го треугольного числа:
- .
Разность между двумя соседними кубическими числами есть центрированное шестиугольное число. Следствие: сумма первых центрированных шестиугольных чисел есть кубическое число [53].
Выражение кубического числа через тетраэдральные[53]:
- , где .
Одна из «гипотез Поллока» (1850 год): каждое натуральное число представимо как сумма не более девяти кубических чисел. Доказана в начале XX века. Обычно достаточно семи кубов, но 15 чисел требуют восьми (15, 22, 50, 114, 167, 175, 186, 212, 231, 238, 303, 364, 420, 428, 454, последовательность A018889 в OEIS), а двум числам нужны все девять: 23 и 239. Если, кроме сложения, допускать вычитание, то достаточно и пяти кубов (возможно, что даже четырёх, но это пока не доказано)[54].
Производящая функция кубических чисел имеет вид[53]:
- ; .
Октаэдральные числа[править | править код]
Додекаэдральные числа[править | править код]
Икосаэдральные числа[править | править код]
Многомерные обобщения[править | править код]
Описанные выше трёхмерные конструкции можно обобщить на четыре и более измерений. Аналогом тетраэдральных чисел в -мерном пространстве служат «симплексные числа», называемые также гипертетраэдральными[55]:
- .
Их частным случаем выступают:
Другие разновидности многомерных чисел — гиперкубические: . Четырёхмерные гиперкубические числа называются биквадратными[55].
Числа из более чем одной разновидности[править | править код]
Некоторые фигурные числа могут принадлежать более чем одной разновидности плоских и/или многомерных чисел, примеры для плоских чисел уже приводились выше. Для многомерных чисел это довольно редкая ситуация[56].
- Пять чисел (и только они) одновременно треугольные и тетраэдральные (последовательность A027568 в OEIS).
- Четыре числа одновременно треугольные и квадратные пирамидальные (последовательность A039596 в OEIS).
- Три числа одновременно плоские квадратные и тетраэдральные (последовательность A003556 в OEIS).
- Два числа одновременно квадратные плоские и квадратные пирамидальные. Это утверждение получило известность как «гипотеза Люка» или «задача о пушечных ядрах» (1875 год). Полное решение дал в 1918 году Джордж Невилл Ватсон[57].
Никакое натуральное число, кроме 1, не может быть одновременно[58][56]:
- треугольным и кубическим;
- треугольным и биквадратным[59];
- треугольным и пятой степенью целого числа[58];
- центрированным шестиугольным и кубическим.
В 1988 году Ф. Бейкерс и Дж. Топ доказали, что никакое число, кроме 1, не может быть одновременно тетраэдральным и квадратным пирамидальным[60]. Доказано также, что не существует чисел, которые одновременно[56]:
- тетраэдральные и кубические;
- квадратные пирамидальные и кубические;
- тетраэдральные и биквадратные;
- квадратные пирамидальные и биквадратные.
Архаичные виды фигурных чисел[править | править код]
В античные времена, когда арифметика не отделялась от геометрии, пифагорейцы (VI век до н. э.) различали ещё несколько видов фигурных чисел[61].
- Линейные числа — числа, «измеряемые только единицей», то есть, в современной терминологии, простые числа (у Евклида используется термин «первые числа», др.-греч. πρώτοι αριθμοί).
- Плоские (или плоскостные) числа — числа, представимые в виде произведения двух сомножителей, бо́льших единицы, то есть составные.
- Частным случаем являются прямоугольные числа (в источниках иногда называются «продолговатыми», англ. oblong), представляющие собой произведение двух последовательных целых чисел[62], то есть имеющие вид
- Телесные числа — числа, представимые произведением трёх сомножителей, бо́льших единицы.
Комментатор Евклида Д. Д. Мордухай-Болтовской поясняет[63]:
Термины «плоскостное» и «телесное» число являются, вероятно, пережитком более раннего периода математической мысли, когда число и геометрический образ были ещё теснее связаны, когда произведение числа предметов на абстрактное число мыслилось как расположение этих предметов в рядах по предметов в каждом, с заполнением площади прямоугольника. То же следует сказать и о произведении трёх чисел, являющемся, согласно евклидовской терминологии, телесным числом.
В настоящее время простые числа не относят к фигурным, а термины «плоское число» и «телесное число» вышли из употребления[63].
Роль в теории чисел[править | править код]
Треугольник Паскаля[править | править код]
Числа из треугольника Паскаля обнаруживают связь со многими разновидностями фигурных чисел.
На третьей линии в треугольнике Паскаля находятся треугольные числа, а на четвёртой — тетраэдральные числа (см. рисунок). Это объясняется тем, что -е тетраэдральное число есть сумма первых треугольных чисел, которые расположены на третьей линии. Аналогично на пятой линии расположены четырёхмерные пентатопные числа и т. д. Все они, как и прочие числа внутри треугольника Паскаля, являются биномиальными коэффициентами.
Таким образом, все внутренние элементы треугольника Паскаля являются фигурными числами, причём представлены различные их разновидности. Вдоль каждой строки, слева направо, идут гипертетраэдральные числа возрастающей размерности. Известно, что сумма всех чисел -й строки равна отсюда следует, что сумма всех чисел первых строк равна числу Мерсенна Следовательно, число Мерсенна можно представить как сумму гипертетраэдральных чисел[64].
Другие применения[править | править код]
Многие теоремы теории чисел допускают формулировку в терминах фигурных чисел. Например, гипотеза Каталана утверждает, что среди гиперкубических чисел произвольных размерностей только одна пара отличается на 1: (доказано в 2002 году)[65].
Всякое чётное совершенное число является треугольным[66] (и одновременно шестиугольным, причём номер шестиугольного числа есть степень двойки). Такое число не может одновременно быть квадратным, кубическим или иным гиперкубическим числом[67].
Гипотеза Лежандра (1808 год, она же третья проблема Эдмунда Ландау): между последовательными квадратными числами всегда найдётся простое число. До сих пор не доказана.
Сумма первых центрированных треугольных чисел есть «магическая константа» для магического квадрата размерности . Другие способы получить эту же константу — через треугольное число , или сложить все натуральные числа от до включительно[68].
Число Мерсенна, большее 1, не может быть квадратным, кубическим или иным гиперкубическим, но может быть треугольным. Треугольных чисел Мерсенна всего четыре: , их поиск эквивалентен решению в натуральных числах уравнения Рамануджана — Нагеля: . Как оказалось, решение этого уравнения существует только при (последовательность A060728 в OEIS), и при соответствующее число Мерсенна будет тогда треугольным[64].

Число Ферма также не может быть квадратным, кубическим или иным гиперкубическим, но в единственном случае может быть треугольным: . Число Ферма также не может быть тетраэдральным и гипертетраэдральным любой размерности выше 2-й[64].
Среди чисел Фибоначчи имеются только три квадратных числа (0, 1 и 144) и четыре треугольных (1, 3, 21, 55, последовательность A039595 в OEIS). Если повернуть треугольник Паскаля, как показано на рисунке, то числа Фибоначчи можно получить как суммы вдоль восходящих диагоналей; этот факт даёт разложение числа Фибоначчи по гипертетраэдральным числам[69].
Среди чисел Люка квадратных чисел два (1 и 4), а треугольных три (1, 3, 5778)[69].
Числа Каталана выражаются через гипертетраэдральные числа следующим образом[70]:
- .
Ещё один класс чисел, тесно связанных с фигурными — числа Стирлинга второго рода . Этот класс включает все треугольные числа: , а выражение равно 2-му по порядку -мерному гиперкубическому числу . Наконец, всякое -мерное гиперкубическое число разлагается по следующим образом[70]:
- .
Примечания[править | править код]
- ↑ Деза Е., Деза М., 2016, с. 9.
- ↑ История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 68. — 352 с.
- ↑ Фигурные числа // Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 607. — 847 с.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 10.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 12—13.
- ↑ Ожигова Е. П. Что такое теория чисел. — М.: Знание, 1970. — С. 56—57.
- ↑ Арифметический ряд // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 1. Архивировано 13 ноября 2013 года.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 15.
- ↑ За страницами учебника математики, 1996, с. 50.
- ↑ 1 2 3 4 5 Деза Е., Деза М., 2016, с. 217.
- ↑ Sameen Ahmed Khan. Sums of the powers ofreciprocals of polygonal numbers (формула 23)
- ↑ Деза Е., Деза М., 2016, с. 14.
- ↑ Диофант Александрийский. Арифметика и Книга о многоугольных числах / Пер. И. Н. Веселовского; Ред. и коммент. И. Г. Башмаковой. — М.: Наука, 1974. — С. 48. — 328 с. Архивировано 24 апреля 2007 года.
- ↑ 1 2 Матвиевская Г. П. Учение о числе на средневековом Ближнем и Среднем Востоке. — Ташкент: ФАН, 1967. — С. 22—23. — 344 с. Вопреки названию, книга прослеживает историю понятия числа с самых древних времён.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 237.
- ↑ Виленкин Н. Я. Популярная комбинаторика. — М.: Наука, 1975. — С. 10—11. — 208 с. Архивировано 5 июня 2016 года.
- ↑ Деза Е., Деза М., 2016, с. 10.
- ↑ Деза Е., Деза М., 2016, с. 19—24.
- ↑ Dickson, 2005, p. 27.
- ↑ Weisstein, Eric W. Telescoping Sum (англ.) на сайте Wolfram MathWorld.
- ↑ Dickson, 2005, p. 3.
- ↑ Деза Е., Деза М., 2016, с. 225.
- ↑ Деза Е., Деза М., 2016, с. 19.
- ↑ 1 2 Dickson, 2005, p. 2.
- ↑ Некоторые конечные числовые ряды. Math24.ru. Дата обращения: 14 июня 2019. Архивировано 14 июня 2019 года.
- ↑ Кохась К. П. Сумма обратных квадратов // Математическое просвещение. — 2004. — Вып. 8. — С. 142—163.
- ↑ Вайнштейн Ф. В. Разбиение чисел. : [арх. 9 августа 2019] // Журнал «Квант». — 1988. — № 11.
- ↑ Деза Е., Деза М., 2016, с. 22.
- ↑ 1 2 3 Деза Е., Деза М., 2016, с. 37—38.
- ↑ В самом деле, пусть (все числа целые) есть целое , причём , — взаимно просты. Умножая обе части на , получим: . Справа — целое число, поэтому делит , и, согласно обобщённой лемме Евклида, делит .
- ↑ 1 2 3 Деза Е., Деза М., 2016, с. 38—39.
- ↑ Деза Е., Деза М., 2016, с. 17—19.
- ↑ Деза Е., Деза М., 2016, с. 33.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 34—37.
- ↑ Деза Е., Деза М., 2016, с. 25—34.
- ↑ Lawrence Downey, Boon W. Ong. Beyond the Basel Problem: Sums ofReciprocals of Figurate Numbers Архивная копия от 29 декабря 2019 на Wayback Machine
- ↑ Деза Е., Деза М., 2016, с. 39—40.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 40—41.
- ↑ Деза Е., Деза М., 2016, с. 42.
- ↑ Деза Е., Деза М., 2016, с. 43.
- ↑ Деза Е., Деза М., 2016, с. 44—46.
- ↑ Деза Е., Деза М., 2016, с. 45—46.
- ↑ Деза Е., Деза М., 2016, с. 46.
- ↑ Dickson, 2005, p. 23.
- ↑ Деза Е., Деза М., 2016, с. 48.
- ↑ Деза Е., Деза М., 2016, с. 70—71.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 76.
- ↑ Деза Е., Деза М., 2016, с. 74—75.
- ↑ Деза Е., Деза М., 2016, с. 239.
- ↑ Frederick Pollock. On the extension of the principle of Fermat's theorem on the polygonal numbers to the higher order of series whose ultimate differences are constant. With a new theorem proposed, applicable to all the orders (англ.) // Abstracts of the Papers Communicated to the Royal Society of London : journal. — 1850. — Vol. 5. — P. 922—924. — .
- ↑ Robitaille, David F. Mathematics and chess // The Arithmetic Teacher. — 1974. — Vol. 21, no. 5 (май). — P. 396—400. — .
- ↑ 1 2 Деза Е., Деза М., 2016, с. 75.
- ↑ 1 2 3 4 Деза Е., Деза М., 2016, с. 78—81.
- ↑ Деза Е., Деза М., 2016, с. 231—232.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 126—134.
- ↑ 1 2 3 Деза Е., Деза М., 2016, с. 77—78.
- ↑ Watson G. N. The Problem of the Square Pyramid // Messenger. Math. 1918. Vol. 48. P. 1-16.
- ↑ 1 2 The Penguin Dictionary of Curious and Interesting Numbers (англ.). Дата обращения: 9 марта 2021.
- ↑ Dickson, 2005, p. 8.
- ↑ Beukers F., Top J. On oranges and integral points on certain plane cubic curves // Nieuw Archief voor Wiskunde (4). — 1988. — Vol. 6, no. 3. — P. 203—210.
- ↑ Гайденко П. П. Эволюция понятия науки (становление и развитие первых научных программ) Архивная копия от 19 августа 2014 на Wayback Machine, глава 1. М.: Наука, 1980.
- ↑ Ben-Menahem, Ari. Historical Encyclopedia of Natural and Mathematical Sciences, Volume 1 : [арх. 11 ноября 2021]. — Springer-Verlag, 2009. — С. 161. — (Springer reference). — ISBN 9783540688310.
- ↑ 1 2 Начала Евклида / Перевод с греческого и комментарии Д. Д. Мордухай-Болтовского при редакционном участии М. Я. Выгодского и И. Н. Веселовского. — М.—Л.: ГТТИ, 1948. — Т. 2. — С. 10, 268—270. — (Классики естествознания).
- ↑ 1 2 3 Деза Е., Деза М., 2016, с. 203—205.
- ↑ Деза Е., Деза М., 2016, с. 196—197.
- ↑ За страницами учебника математики, 1996, с. 51.
- ↑ Деза Е., Деза М., 2016, с. 200—201.
- ↑ Деза Е., Деза М., 2016, с. 222—223.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 208.
- ↑ 1 2 Деза Е., Деза М., 2016, с. 214—215.
Литература[править | править код]
- Виленкин Н. Я., Шибасов Л. П. Шибасова 3. Ф. За страницами учебника математики: Арифметика. Алгебра. Геометрия. — М.: Просвещение, 1996. — С. 48—52. — 320 с. — ISBN 5-09-006575-6.
- Глейзер Г. И. История математики в школе (4—6 классы). — М.: Просвещение, 1964. — С. 84—86. — 376 с.
- Деза Е. Специальные числа натурального ряда: Учебное пособие.. — М.: Книжный дом «ЛИБРОКОМ», 2011. — 240 с. — ISBN 978-5-397-01750-3.
- Деза Е., Деза М. Фигурные числа. — М.: МЦНМО, 2016. — 349 с. — ISBN 978-5-4439-2400-7.
- Депман И. Я. История арифметики. Пособие для учителей. — Изд. второе. — М.: Просвещение, 1965. — С. 150—155.
- Матвиевская Г. П. Заметки о многоугольных числах в записных книжках Эйлера // Историко-математические исследования. — М.: Наука, 1983. — № 27. — С. 27—49.
- Серпинский В. Пифагоровы треугольники. — М.: Учпедгиз, 1959. — 111 с.
- Стиллвелл Д. Глава 3. Греческая теория чисел // Математика и её история. — Москва-Ижевск: Институт компьютерных исследований, 2004.
- Dickson L. E. Polygonal. pyramidal and figurate numbers // History of the Theory of Numbers. — New York : Dover, 2005. — Vol. 2: Diophantine Analysis. — P. 22—23.
Ссылки[править | править код]
- Фигурные числа. Издательская группа ОСНОВА. Дата обращения: 10 февраля 2021.
- Weisstein, Eric W. Figurate Number (англ.) на сайте Wolfram MathWorld.
- Weisstein, Eric W. Centered Polygonal Numbe (англ.) на сайте Wolfram MathWorld.
Эта статья входит в число избранных статей русскоязычного раздела Википедии. |





































































































































































































![{\displaystyle S_{n}^{[d]}={\frac {(n-1+d)!}{(n-1)!\ d!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28a47962c7f0baec91883adc82aeda56e4695839)
![{\displaystyle S_{n}^{[2]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75baa5e8e4f48950b9f95e7ea0835c86332aead5)
![{\displaystyle S_{n}^{[3]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f84359e60c6739fcab45e20313d1a9c15fb08fd1)
![{\displaystyle S_{n}^{[4]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d44ef89cadef001a85fd17138679ec391a436e2d)
![{\displaystyle Q_{n}^{[d]}=n^{d}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/994da48a0b29edfff10ede51a2387ff370b62a11)






















![{\displaystyle Cat_{n}=S_{n+1}^{[n]}-S_{n+2}^{[n-1]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e303a9fc2b2d32f4a8e53599babb6e2ada6ef0e9)



![{\displaystyle Q_{2}^{[n]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8afaed0172274299d068445d247c03a3c1c16c9a)
![{\displaystyle Q_{n}^{[d]}=\sum _{m=0}^{d}{S(d,m)n(n-1)\dots (n-m+1)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/52d9f9637833e09aa2d6a5d27d278891ea9a0ee9)





