Ряд (математика)

Ряд (бесконе́чная су́мма) в математике — одно из центральных понятий математического анализа, математическая концепция, представляющая собой сумму бесконечного числа слагаемых, упорядоченных в определённой последовательности. В простейшем случае ряд записывается как бесконечная сумма чисел[1][2]:
- Краткая запись:
- (иногда нумерацию слагаемых начинают не с 1, а с нуля).
Слагаемые тогда представляют собой последовательность вещественных или комплексных чисел. Обрывая бесконечный ряд на -м члене, получаем частичные суммы:
Если для последовательности частичных сумм определён конечный предел: то значение называется суммой данного ряда, а сам ряд называется сходящимся (в противном случае — расходящимся)[3].
При более общем подходе ряд понимается как последовательность элементов (членов данного ряда) некоторого топологического векторного пространства, рассматриваемая вместе с множеством частичных сумм членов ряда (частичные суммы определяются так же, как и в числовых рядах). Например, если в качестве элементов ряда используются функции, то говорят о функциональных рядах.
Числовые ряды и их обобщения используются повсеместно в математическом анализе для вычислений, анализа поведения разнообразных функций, в частности при решении алгебраических или дифференциальных уравнений. Разложение функции в ряд можно рассматривать как обобщение задания вектора координатами, эта операция позволяет свести исследование сложной функции к анализу элементарных функций и облегчает численные расчёты[4].
Ряды — незаменимый инструмент исследования не только в математике, но и в физике, информатике, статистике и других науках[4][2][5]. Широкое использование аппарата рядов характерно, например, для небесной механики[6], оптики, теории упругости[7], теории теплопроводности (именно для этого раздела физики были первоначально разработаны ряды Фурье), в теории электромагнетизма[8], в ядерной физике[9], в экономике[10].
Эпизодическое использование бесконечных рядов (в основном прогрессий) отмечается с античных времён. Основы систематической теории разложения функций в ряды разработал Ньютон в конце XVII века, для него она стала основным инструментом работы с неэлементарными и неявно заданными функциями. С помощью рядов Ньютон выполнял, в частности, интегрирование функций и решение дифференциальных уравнений. В дальнейшем большой вклад в тематику внесли Эйлер, Коши, Фурье и другие математики[11].
Числовые ряды[править | править код]
Сходимость и сумма ряда[править | править код]
Чтобы присвоить числовому ряду:
значение суммы, необходимо рассмотреть последовательность «частичных сумм», которые получаются, если оборвать бесконечную сумму на каком-то члене:
Если последовательность частичных сумм имеет предел (конечный или бесконечный), то говорят, что сумма ряда равна При этом, если предел конечен, то говорят, что ряд сходится. Если предел не существует или бесконечен, то говорят, что ряд расходится[1].
Для выяснения ключевого в анализе вопроса, сходится или нет заданный ряд, предложены многочисленные признаки сходимости.
Примеры[править | править код]
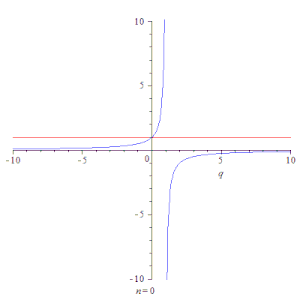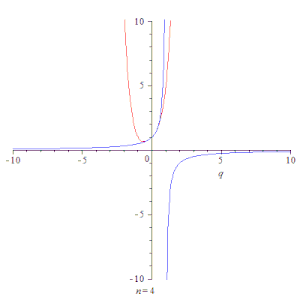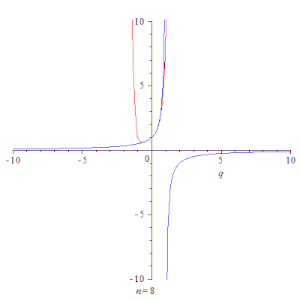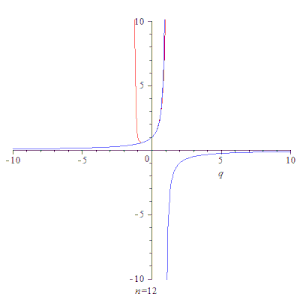
Простейшим примером сходящегося ряда является сумма членов бесконечной геометрической прогрессии[12] со знаменателем :
Частичная сумма Предел этого выражения это и есть сумма бесконечной геометрической прогрессии[1]. Например, при получается ряд, сумма которого равна 2:
Десятичную дробь с бесконечной дробной частью можно рассматривать как сумму ряда[12]; например, число есть сумма следующего ряда:
Более сложным примером является ряд обратных квадратов, сумму которого лучшие математики Европы не могли найти более 100 лет[13]:
Ряд расходится, сумма его бесконечна. Расходится и гармонический ряд: «Ряд Гранди» расходится, его частичные суммы колеблются от 1 до 0, поэтому предела частичных сумм не существует, суммы у этого ряда нет[14].
Классификация[править | править код]
Положительный ряд[15] — вещественный ряд, все члены которого неотрицательны. У положительных рядов сумма всегда существует, но может быть бесконечна[16].
Знакочередующийся ряд — вещественный ряд, в котором знаки членов чередуются: плюс, минус, плюс, минус и т. д. Для таких рядов существует простой признак сходимости Лейбница. Знакочередующийся вариант приведенного выше гармонического ряда, в отличие от последнего, сходится[17]:
Абсолютная и условная сходимость[править | править код]
Говорят, что вещественный или комплексный ряд сходится абсолютно, если сходится ряд из модулей (абсолютных величин) его членов[17]:
Абсолютно сходящийся ряд сходится и в обычном смысле этого понятия. При этом всякий такой ряд обладает важным свойством переместительности: при любой перестановке членов абсолютно сходящегося ряда получается сходящийся ряд с той же суммой[18]. В частности, у положительных сходящихся рядов можно как угодно переставлять члены ряда, на сходимость и на сумму это не влияет[19].
Если числовой ряд сходится, но не абсолютно, он называется условно сходящимся. Пример:
- Сам ряд сходится, но ряд его абсолютных величин (гармонический ряд) расходится[17].
Свойства условно сходящихся рядов[17].
- Если ряд сходится условно, то как ряд из его положительных членов, так и ряд из его отрицательных членов расходятся.
- Следствие (критерий абсолютной сходимости): ряд из вещественных чисел сходится абсолютно тогда и только тогда, когда сходятся как ряд из положительных его членов, так и ряд из отрицательных членов.
- (теорема Римана): Перестановкой членов условно-сходящегося ряда можно получить ряд с любой заданной вещественной суммой.
Операции над рядами[править | править код]
Пусть заданы сходящиеся ряды и . Тогда:
- Их суммой называется ряд разностью — ряд
- Если оба ряда сходятся к и соответственно, то их сумма и разность также сходятся. Сумма сходящегося и расходящегося рядов всегда расходится[20]:
- ,
- Если оба ряда сходятся абсолютно, то сумма и разность этих рядов также сходятся абсолютно[21].
- Их произведением Коши называется ряд , где:
- Если хотя бы один из исходных рядов сходится абсолютно, то произведение рядов сходится[22].
Необходимый признак сходимости числового ряда[править | править код]
Ряд может сходиться лишь в том случае, когда член (общий член ряда) с возрастанием его номера стремится к нулю[23]:
Это необходимый признак сходимости ряда, но он не является достаточным — у гармонического ряда, например, общий член с ростом номера неограниченно уменьшается, тем не менее ряд расходится. Если же общий член ряда не стремится к нулю, то ряд заведомо расходится[23].
Сходящиеся ряды[править | править код]
Свойство 1. Если ряд
- (1.1)
сходится и его сумма равна , то ряд
- (1.2)
где — произвольное число, также сходится и его сумма равна . Если же ряд (1.1) расходится и , то ряд (1.2) расходится.
Свойство 2 (ассоциативный закон). В сходящемся ряде можно произвольно объединять соседние члены в группы без нарушения их порядка[24].
Этим свойством можно воспользоваться для доказательства расходимости ряда: если после указанной группировки получается расходящийся ряд, то и исходный ряд также расходится.
Нерешённые проблемы[править | править код]
До сих пор неизвестно, сходится ли «ряд Флинт Хиллз» (Flint Hills Series)[25]:
Если удастся доказать, что этот ряд сходится, то как следствие получится важный факт: мера иррациональности числа меньше, чем 2,5.
Известно, что сумма ряда обратных квадратов и суммы других рядов с обратными чётными степенями выражаются через степени числа но мало что известно про сумму обратных кубов («константу Апери»):
- .
Никто пока не сумел связать это значение с классическими константами или элементарными функциями[26].
Ряды с нечисловыми членами[править | править код]
Понятие бесконечного ряда и его суммы можно ввести не только для чисел, но и для других математических объектов, для которых определены сложение и понятие близости, позволяющее определить предел. При таком подходе ряд понимается как последовательность элементов (членов данного ряда) некоторого топологического векторного пространства, рассматриваемая вместе с множеством частичных сумм членов ряда (частичные суммы определяются так же, как и в числовых рядах)[3].
Например, в анализе широко используются ряды из функций: степенные ряды, ряды Фурье, ряды Лорана. Членами ряда могут быть также векторы, матрицы и др. Такие ряды всегда можно почленно складывать или вычитать, причём сумма и разность сходящихся рядов также сходятся. Если члены рядов берутся из кольца или поля, то ряды сами образуют кольцо относительно сложения и произведения Коши[3].
Функциональные ряды[править | править код]
Определение и свойства[править | править код]
Ряд называется функциональным, если все его члены — функции, определённые на некотором множестве[4]:
- краткая запись:
Частичные суммы в этом случае также являются функциями, заданными на том же множестве. Ряд называется сходящимся на множестве , если при любом фиксированном сходится числовой ряд[4]:
Множество называется областью сходимости ряда[4]. Сумма ряда, очевидно, также является функцией на
Пример — разложение в ряд рациональной дроби:
Этот ряд сходится в интервале .
Среди основных типов функциональных рядов[4]:
- степенные ряды (в частности, ряды Тейлора);
- тригонометрические ряды; в частности, ряды Фурье;
- ряды Лорана.
Кроме определённой выше «поточечной» сходимости, в разных пространствах могут быть использованы и другие нормы близости, от которых зависит существование предела частичных сумм. Например, можно определить «чебышёвскую норму»[27].
Равномерная сходимость[править | править код]
Вообще говоря, свойства суммы могут отличаться от свойств членов ряда — например, сумма ряда непрерывных функций может не быть непрерывной[28].
Говорят, что сходящийся на множестве функциональный ряд равномерно сходится (на этом множестве)[29], если последовательность частичных сумм ряда равномерно сходится на .
Существуют несколько признаков, позволяющих убедиться в равномерной сходимости ряда[29]:
Важность понятия равномерной сходимости ряда показывают следующие теоремы (все функции считаются вещественными).
- Сумма ряда из функций, непрерывных в некоторой точке , будет и сама непрерывна в этой точке при условии, что функциональный ряд в точке сходится равномерно. В частности, сумма равномерно сходящегося ряда вещественных функций, непрерывных на отрезке также будет непрерывна на этом отрезке[30].
- Если функции непрерывно дифференцируемы на отрезке и оба ряда:
- сходятся на , причём ряд производных сходится равномерно, то сумма ряда имеет производную, и дифференцировать ряд можно почленно[31]:
- Если функции непрерывны на отрезке и ряд сходится на равномерно к функции то интегрировать ряд можно почленно[32]:
- Условие равномерной сходимости гарантирует, что ряд справа сходится.
- Если функции интегрируемы по Риману на отрезке и ряд сходится на равномерно к функции то сумма ряда также будет интегрируема по Риману[32].
Пример неравномерно сходящегося степенного ряда — геометрическая прогрессия В промежутке она сходится к функции но не равномерно (о чём свидетельствует бесконечный скачок суммы при приближении к 1)[33].
Ряды матриц[править | править код]
В кольце числовых квадратных матриц фиксированного порядка назовём -окрестностью матрицы множество матриц, все компоненты которых отличаются от соответствующих компонент меньше, чем на Опираясь на такую топологию, предел последовательности матриц определяется покомпонентно[34], то есть матрица является пределом последовательности матриц , если каждая её компонента является пределом соответствующей последовательности
Теперь можно определить по общим правилам ряды из числовых матриц, понятие сходимости ряда (в том числе абсолютной сходимости) и суммы сходящегося ряда. Другими словами, ряд матриц порядка сходится, если сходятся рядов его компонент, и суммой будет матрица, содержащая соответствующие пределы этих рядов[34].
Степенной ряд для матриц имеет вид[34]:
где — заданные числовые коэффициенты, — единичная матрица, — матрица неизвестных. Этот ряд равносилен системе из числовых рядов. Для оценки его сходимости составим обычный степенной ряд из комплексных чисел:
Пусть радиус сходимости этого ряда равен Тогда верны следующие теоремы[34]:
- Матричный степенной ряд абсолютно сходится для всех матриц, находящихся в - окрестности нулевой матрицы, где
- Если матричный степенной ряд сходится в области где — матрица с положительными компонентами, — матрица модулей неизвестных, то он в этой области сходится абсолютно.
Пример степенного ряда из матриц см. в статье Экспонента матрицы. С помощью рядов можно определить стандартные функции для квадратных матриц (например, синус).
Вариации и обобщения[править | править код]
Обобщением понятия ряда является понятие двойного ряда, члены которого нумеруются не одним, а двумя индексами[35].
Обобщением понятия суммы ряда является понятие суммирующей функции ряда, выбор которой делает понятие суммы расходящегося (в классическом смысле) ряда приемлемым. Предложено множество вариантов такого обобщения: сходимость по Пуассону — Абелю, Борелю, Чезаро, Эйлеру, Ламберту и другие[36].
История[править | править код]
Античный период[править | править код]

Античные математики, в соответствии с пифагорейской идеологией, отвергали все актуально бесконечные понятия, в том числе и бесконечные ряды. Тем не менее некоторые ограниченные применения понятия ряда имели место. Например, Архимед для вычисления площади сегмента параболы фактически нашёл сумму бесконечной геометрической прогрессии[37]:
Ван дер Варден пишет об этом: «Архимед не говорит о сумме бесконечно убывающей геометрической прогрессии, ему ещё не известно выражение „сумма бесконечного ряда“, однако он прекрасно владеет сущностью этого понятия». В нескольких решённых Архимедом задачах на вычисление площади или объёма он использует, в современной терминологии, верхние и нижние интегральные суммы с неограниченно возрастающим числом членов. Из-за отсутствия понятия предела для обоснования результата использовался громоздкий метод исчерпывания[37].
Керальская школа[править | править код]
Математики Индии, не связанные пифагорейскими ограничениями, существенно продвинули теорию рядов и успешно её применяли. Наибольшего успеха в XV—XVI веках добилась Керальская школа астрономии и математики (южная Индия). Для астрономических вычислений керальцы смогли впервые в истории найти разложение тригонометрических и иных функций в бесконечные ряды[38]:
Общей теории таких разложений у них, впрочем, не было, для получения этих формул было проведено спрямление дуги окружности[39][40].
Из ряда для арктангенса керальцы получили хорошее приближение для числа с десятью знаками[39]:
В Европе достижения керальской школы долгое время оставались неизвестными и были переоткрыты независимо. Ряд для арктангенса впервые опубликовал Джеймс Грегори в 1671 году, а ряды для синуса и косинуса — Исаак Ньютон в 1666 году[39].
XVII век[править | править код]
До примерно XVII века бесконечные ряды в трудах европейских математиков появлялись редко. Заслуживает упоминания труд английского математика XIV века Ричарда Суайнсхеда, который просуммировал ряд[41]:
В XVII веке бесконечные ряды уже вызывают общий интерес и начинают использоваться при решении многих практических задач — приближённые вычисления, интерполирование, теория логарифмов и др.

В 1647 году Грегуар де Сен-Венсан обнаружил связь логарифма и площади под гиперболой (см. рисунок). В 1650 году, исходя из геометрических соображений, итальянский математик Пьетро Менголи опубликовал в трактате «Новые арифметические квадратуры» разложение в бесконечный ряд[42]:
Менголи исследовал также другие ряды и доказал, что гармонический ряд расходится; Он также показал, что ряд обратных квадратов сходится, хотя не смог найти его сумму[42].
В 1668 году немецкий математик Николас Меркатор (Кауфман), проживавший тогда в Лондоне, в трактате «Logarithmotechnia» впервые рассмотрел разложение в ряд не числа, а функции, тем самым положив начало теории степенных рядов[42]:
Как универсальный инструмент исследования функций и численных расчётов бесконечные ряды использовали Исаак Ньютон и Готфрид Вильгельм Лейбниц, создатели математического анализа. Ещё в середине XVII века Ньютон и Грегори открыли биномиальное разложение для любого, не только целого показателя степени (впервые опубликован в «Алгебре» Валлиса, 1685 год)[43]:
Ряд сходится при С помощью этой формулы Ньютон сумел впервые выполнить вычисление дуги эллипса в виде ряда (в современной терминологии, он вычислил эллиптический интеграл)[44]. Ньютон также показал, как с помощью рядов решать уравнения, включая дифференциальные уравнения первого порядка, и исследовать интегралы, не выражающиеся через элементарные функции[45].
К концу XVII века стали известны разложения в ряды всех элементарных функций. Лейбниц и Грегори открыли (1674) первое в Европе разложение числа (ряд Лейбница)[46]:
На рубеже веков (1689—1704) ученик Лейбница Якоб Бернулли опубликовал первую монографию в пяти томах под заголовком «Арифметические предложения о бесконечных рядах и их конечных суммах» (Propositiones arithmeticae de seriebus infinitis carumque summa finita). Он показал применение рядов для решения самых разнообразных задач[47].
XVIII—XIX века[править | править код]
В 1715 году Брук Тейлор опубликовал фундаментальный ряд Тейлора (давно известный, впрочем, Грегори и Ньютону)[48].
Огромный вклад в теорию рядов внёс Леонард Эйлер. Он первым сумел найти сумму ряда обратных квадратов, разработал методы улучшения сходимости рядов, начал исследование тригонометрических рядов, предложил понятие обобщённой суммы ряда, пригодное для расходящихся рядов. Само понятие «аналитической функции» было связано с возможностью её представления в виде степенного ряда[49].
В XIX веке Коши и Вейерштрасс построили строгие основания анализа и, в частности, строгую теорию рядов. Было введено важное понятие равномерной сходимости, сформулированы разнообразные признаки сходимости[50].
Бурное развитие получили теория тригонометрических рядов. Ещё Даниил Бернулли высказал убеждение, что любую (непрерывную) функцию на заданном промежутке можно представить тригонометрическим рядом[51]. Дискуссии на эту тему продолжались до 1807 года, когда Фурье опубликовал теорию представления произвольных кусочно-аналитических функций тригонометрическими рядами (окончательный вариант содержится в его «Аналитической теории тепла», 1822). Для разложения функции в ряд Фурье привёл интегральные формулы расчёта коэффициентов. Изложение Фурье не было строгим в современном понимании, но уже содержало исследование сходимости большинства полученных им рядов[52]. В 1868 году Бернхард Риман использовал ряды для строгого определения определённого интеграла[53].
Одновременно широкое развитие и применение в XIX веке получили ряды в комплексном анализе, в том числе ряды Лорана[54][55].
В XX веке понятие ряда было распространено на широкий класс математических объектов, не обязательно числовых, в том числе векторы и квадратные матрицы[34][56].
Примечания[править | править код]
- ↑ 1 2 3 Фихтенгольц, 1966, с. 257—258.
- ↑ 1 2 БРЭ.
- ↑ 1 2 3 Математическая энциклопедия, 1984, с. 1063.
- ↑ 1 2 3 4 5 6 Математическая энциклопедия, 1984, с. 1068—1070.
- ↑ Пучков Н. П., Жуковская Т. В. и др. Интегральное исчисление. Ряды. Дифференциальные уравнения // Применение математических знаний в профессиональной деятельности. Тамбовский государственный технический университет. Дата обращения: 22 июля 2023. Архивировано 22 июля 2023 года.
- ↑ Дубошин Г. Н. Небесная механика. Основные задачи и методы. — 2-е изд. — М.: Наука, 1968. — С. 150. — 800 с.
- ↑ Воробьёв, 1979, с. 361—407.
- ↑ Погребысский И. Б. От Лагранжа к Эйнштейну. Классическая механика XIX ст.. — М.: Наука, 1966. — С. 274. — 328 с.
- ↑ Очерки по истории развития ядерной физики в СССР. — Киев: Наукова думка, 1982. — С. 81. — 332 с.
- ↑ T. Arens, Fr. Hettich, Ch. Karpfinger, U. Kockelhorn, K. Lichtenegger, H. Stachel. Mathematik. — 5-е изд. — Berlin / Heidelberg, 2022. — P. 290.
- ↑ МЭС, 1988, с. 536—537.
- ↑ 1 2 Фихтенгольц, 1966, с. 258—259.
- ↑ Воробьёв, 1979, с. 52, 178.
- ↑ Воробьёв, 1979, с. 32—33, 52—53.
- ↑ Выгодский, 1977, с. 540.
- ↑ Воробьёв, 1979, с. 50—71.
- ↑ 1 2 3 4 Воробьёв, 1979, с. 72—85.
- ↑ Фихтенгольц, 1966, с. 315.
- ↑ Виленкин и др., 1982, с. 55.
- ↑ Виленкин и др., 1982, с. 15.
- ↑ Виленкин и др., 1982, с. 67, упр. 56.
- ↑ Rudin, Walter. Principles of Mathematical Analysis. — McGraw-Hill, 1976. — P. 74.
- ↑ 1 2 Воробьёв, 1979, с. 38—39.
- ↑ Воробьёв, 1979, с. 40—41.
- ↑ Flint Hills Series. Дата обращения: 11 мая 2019. Архивировано 11 мая 2019 года.
- ↑ Weisstein, Eric W. Apéry's constant (англ.) на сайте Wolfram MathWorld.
- ↑ Виленкин и др., 1982, с. 80—82.
- ↑ Виленкин и др., 1982, с. 86, упр. 70.
- ↑ 1 2 Фихтенгольц, 1966, с. 428—432.
- ↑ Фихтенгольц, 1966, с. 430—432.
- ↑ Фихтенгольц, 1966, с. 438—439.
- ↑ 1 2 Фихтенгольц, 1966, с. 436—438.
- ↑ Фихтенгольц, 1966, с. 424.
- ↑ 1 2 3 4 5 Смирнов В. И. Курс высшей математики. — 10-е изд.. — СПб.: БХВ-Петербург, 2010. — Т. 3 часть 2. — С. 369—374. — 816 с. — ISBN 978-5-9775-0087-6.
- ↑ Воробьёв, 1979, с. 233—258.
- ↑ Воробьёв, 1979, с. 281—306.
- ↑ 1 2 Ван дер Варден. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. — М.: Наука, 1959. — С. 302—303, 309—310. — 456 с.
- ↑ История математики, том I, 1970, с. 202—203.
- ↑ 1 2 3 История математики, том I, 1970, с. 202—203.
- ↑ Паплаускас А. Б. Доньютоновский период развития бесконечных рядов. Часть I // Историко-математические исследования. — М.: Наука, 1973. — Вып. XVIII. — С. 104—131.
- ↑ История математики, том I, 1970, с. 275.
- ↑ 1 2 3 История математики, том II, 1970, с. 158—166.
- ↑ История математики, том II, 1970, с. 228.
- ↑ История математики, том II, 1970, с. 231.
- ↑ История математики, том II, 1970, с. 246—247.
- ↑ Фихтенгольц, 1966, с. 368.
- ↑ Вилейтнер Г. История математики от Декарта до середины XIX столетия. — М.: ГИФМЛ, 1960. — С. 133. — 468 с.
- ↑ История математики, том III, 1972, с. 294—296.
- ↑ Отрадных Ф. П. Математика XVIII века и академик Леонард Эйлер. — М.: Советская наука, 1954. — 39 с.
- ↑ Математика XIX века. Том II, 1981, с. 173—174, 207.
- ↑ Паплаускас А. Б. Тригонометрические ряды. От Эйлера до Лебега. — М.: Наука, 1966. — С. 26—27. — 277 с.
- ↑ Тригонометрический ряд // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 5.
- ↑ Риман Б. О возможности выражения функции при помощи тригонометрического ряда // Разложение функций в тригонометрические ряды / Лежен-Дирикле, Риманн, Липшиц; Пер. Г. А. Грузинцева и С. Н. Бернштейна. — Харьков: Харьковское математическое общество, 1914. — (Харьковская математическая библиотека. Серия В; № 2).
- ↑ Rodriguez, Rubi; Kra, Irwin; Gilman, Jane P. (2012), Complex Analysis: In the Spirit of Lipman Bers, Graduate Texts in Mathematics, vol. 245, Springer, p. 12—13, ISBN 9781441973238.
- ↑ Математика XIX века. Том II: Геометрия. Теория аналитических функций / Под ред. Колмогорова А. Н., Юшкевича А. П.. — М.: Наука, 1981. — С. 145, 247—254. — 270 с.
- ↑ Шклярский Д. О. Условно сходящиеся ряды векторов // Успехи математических наук. — 1944. — № 10. — С. 51—59.
Литература[править | править код]
- Виленкин Н. Я., Цукерман В. В., Доброхотова М. А., Сафонов А. Н. Ряды. — М.: Просвещение, 1982. — 160 с.
- Воробьев Н. Н. Теория рядов. — 4-е изд. — М.: Наука, 1979. — 408 с.
- Выгодский М. Я. Справочник по высшей математике. — 12-е изд.. — М.: Наука, 1977. — 872 с.
- Зорич В. А.. Глава III. Предел. § 1. Предел последовательности // Математический анализ, часть I. — М.: Наука, 1981. — С. 104—114. — 544 с.
- История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I.
- Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II.
- Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III.
- Математика XIX века. Том II: Геометрия. Теория аналитических функций / Под ред. Колмогорова А. Н., Юшкевича А. П.. — М.: Наука, 1981. — 270 с.
- Письменный Д. Т. Часть 2 // Конспект лекций по высшей математике. — 6-е изд. — М.: Айрис-пресс, 2008.
- Ряд // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1984. — Т. 4. — С. 1063—1070.
- Ряд // Математический энциклопедический словарь. — М.: Советская энциклопедия, 1988. — С. 533—537. — 847 с.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления, в трёх томах. — 6-е изд.. — М.: Наука, 1966. — Т. 2. — 680 с.
Ссылки[править | править код]
- Ряд / Кудрявцев Л. Д., Юшкевич А. П. // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
- Савельева Р. Ю. Высшая математика. Теория рядов.
- Weisstein, Eric W. Series (англ.) на сайте Wolfram MathWorld.
Эта статья входит в число хороших статей русскоязычного раздела Википедии. |




























































![{\displaystyle [a,b],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d493b840f8326ba81ff9d95b4edf1effd5f2842)

![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)











































