Специальная теория относительности
Специа́льная тео́рия относи́тельности (СТО; также ча́стная тео́рия относи́тельности) — теория, описывающая движение, законы механики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света (в рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей). Фактически СТО описывает геометрию четырёхмерного пространства-времени и основана на плоском (то есть неискривлённом) пространстве Минковского. Обобщение СТО для сильных гравитационных полей называется общей теорией относительности.
Основным отличием СТО от классической механики является зависимость (наблюдаемых) пространственных и временных характеристик от скорости. Описываемые специальной теорией относительности отклонения в протекании физических процессов от предсказаний классической механики называют релятивистскими эффектами, а скорости, при которых такие эффекты становятся существенными, — релятивистскими скоростями.
Центральное место в специальной теории относительности занимают преобразования Лоренца, позволяющие преобразовывать пространственно-временные координаты событий при переходе от одной инерциальной системы отсчёта к другой, когда одна из них движется относительно другой с определенной скоростью.
Специальная теория относительности была создана Альбертом Эйнштейном в работе 1905 года «К электродинамике движущихся тел». Математический аппарат преобразований координат и времени между различными системами отсчёта (с целью сохранения уравнений электромагнитного поля) был ранее сформулирован французским математиком А. Пуанкаре (который и предложил их назвать «преобразованиями Лоренца»: сам Лоренц вывел до этого только приближённые формулы[К. 1]). А. Пуанкаре также первым показал, что эти преобразования можно геометрически представить как повороты в четырёхмерном пространстве-времени (опередив Г. Минковского), и показал, что преобразования Лоренца образуют группу (см. о роли Пуанкаре в создании теории относительности подробнее).
Непосредственно термин «теория относительности» был предложен М. Планком. В дальнейшем, после разработки А. Эйнштейном теории гравитации — общей теории относительности — к первоначальной теории начал применяться термин «специальная» или «частная» теория относительности (от нем. Spezielle Relativitätstheorie).
Создание СТО[править | править код]
Предпосылкой к созданию теории относительности явилось развитие в XIX веке электродинамики[1]. Результатом обобщения и теоретического осмысления экспериментальных фактов и закономерностей в областях электричества и магнетизма стали уравнения Максвелла, описывающие свойства электромагнитного поля и его взаимодействие с зарядами и токами. В электродинамике Максвелла скорость распространения электромагнитных волн в вакууме не зависит от скоростей движения как источника этих волн, так и наблюдателя, и равна скорости света. Таким образом, уравнения Максвелла оказались неинвариантными относительно преобразований Галилея, что противоречило классической механике.
Специальная теория относительности была разработана в начале XX века усилиями Г. А. Лоренца, А. Пуанкаре, А. Эйнштейна и других учёных [2] (см. История теории относительности). Экспериментальной основой для создания СТО послужил опыт Майкельсона. Результаты оказались неожиданными для классической физики того времени: скорость света не зависит от направления (изотропность) и орбитального движения Земли вокруг Солнца. Попытка интерпретировать полученные данные вылилась в пересмотр классических представлений и привела к созданию специальной теории относительности.
При движении со скоростями, всё более приближающимися к скорости света, отклонение от законов классической динамики становится всё более существенным. Второй закон Ньютона, связывающий силу и ускорение, должен быть модифицирован в соответствии с принципами СТО. Также импульс и кинетическая энергия тела сложнее зависят от скорости, чем в нерелятивистском случае.
Специальная теория относительности получила многочисленные подтверждения на опыте и является верной теорией в своей области применимости[3] (см. Экспериментальные основания СТО). По меткому замечанию Л. Пэйджа, «в наш век электричества вращающийся якорь каждого генератора и каждого электромотора неустанно провозглашает справедливость теории относительности — нужно лишь уметь слушать»[4].
Основные понятия и постулаты СТО[править | править код]
Специальная теория относительности, как и любая другая физическая теория, может быть сформулирована на базе из основных понятий и постулатов (аксиом) и правил соответствия её физическим объектам.
Основные понятия[править | править код]
Система отсчёта представляет собой некоторое материальное тело, выбираемое в качестве начала этой системы, способ определения положения объектов относительно начала системы отсчёта и способ измерения времени. Обычно различают системы отсчёта и системы координат. Добавление процедуры измерения времени к системе координат «превращает» её в систему отсчёта.
Инерциальная система отсчёта (ИСО) — такая система, относительно которой объект, не подверженный внешним воздействиям, движется равномерно и прямолинейно. Постулируется, что ИСО существуют, и любая система отсчёта, движущаяся относительно данной инерциальной системы равномерно и прямолинейно, также является ИСО.
Событием называется любой физический процесс, который может быть локализован в пространстве, и имеющий при этом очень малую длительность. Другими словами, событие полностью характеризуется координатами (x, y, z) и моментом времени t. Примерами событий являются: вспышка света, положение материальной точки в данный момент времени и т. п.
Обычно рассматриваются две инерциальные системы S и S'. Время и координаты некоторого события, измеренные в системе S, обозначаются как (t, x, y, z), а координаты и время этого же события, измеренные в системе S', как (t', x', y', z'). Удобно считать, что координатные оси систем параллельны друг другу, и система S' движется вдоль оси x системы S со скоростью v. Одной из задач СТО является поиск соотношений, связывающих (t', x', y', z') и (t, x, y, z), которые называются преобразованиями Лоренца.
Синхронизация времени[править | править код]
В СТО постулируется возможность определения единого времени в рамках данной инерциальной системы отсчёта процедурой синхронизации двух часов, находящихся в произвольных точках ИСО[5].
Пусть от первых часов в момент времени ко вторым посылается сигнал (не обязательно световой) с постоянной скоростью . Сразу по достижении вторых часов сигнал отправляется обратно с той же постоянной скоростью и достигает первых часов в момент времени . Часы считаются синхронизированными, если выполняется соотношение , где — показание вторых часов в момент прихода к ним сигнала от первых часов.
Предполагается, что такая процедура в данной инерциальной системе отсчёта может быть проведена для любых двух часов, так что справедливо свойство транзитивности: если часы A синхронизированы с часами B, а часы B синхронизированы с часами C, то часы A и C также окажутся синхронизированными.
В отличие от классической механики, единое время можно ввести только в рамках данной системы отсчёта. В СТО не предполагается, что время является общим для различных систем. В этом состоит основное отличие аксиоматики СТО от классической механики, в которой постулируется существование единого (абсолютного) времени для всех систем отсчёта.
Согласование единиц измерения[править | править код]
Чтобы измерения, выполненные в различных ИСО, можно было между собой сравнивать, необходимо провести согласование единиц измерения между системами отсчёта. Так, единицы длины могут быть согласованы при помощи сравнения эталонов длины в перпендикулярном направлении к относительному движению инерциальных систем отсчёта[6]. Например, это может быть кратчайшее расстояние между траекториями двух частиц, движущихся параллельно осям x и x' и имеющих различные, но постоянные координаты (y, z) и (y',z'). Для согласования единиц измерения времени можно использовать идентично устроенные часы, например, атомные.
Постулаты СТО[править | править код]
В первую очередь в СТО, как и в классической механике, предполагается, что пространство и время однородны, а пространство также изотропно[7]. Если быть более точным (современный подход), инерциальные системы отсчёта собственно и определяются как такие системы отсчёта, в которых пространство однородно и изотропно, а время однородно. По сути существование таких систем отсчёта постулируется.
Постулат 1 (принцип относительности Эйнштейна). Законы природы одинаковы во всех системах координат, движущихся прямолинейно и равномерно друг относительно друга[8]. Это означает, что форма зависимости физических законов от пространственно-временных координат должна быть одинаковой во всех ИСО, то есть законы инвариантны относительно переходов между ИСО. Принцип относительности устанавливает равноправие всех ИСО.
Учитывая второй закон Ньютона (или уравнения Эйлера-Лагранжа в лагранжевой механике), можно утверждать, что если скорость некоторого тела в данной ИСО постоянна (ускорение равно нулю), то она должна быть постоянна и во всех остальных ИСО. Иногда это и принимают за определение инерциальных систем отсчёта.
Формально, принцип относительности Эйнштейна распространяет классический принцип относительности (Галилея) с механических на все физические явления. Однако, если учесть, что во времена Галилея физика заключалась собственно в механике, то и классический принцип тоже можно было считать распространяющимся на все физические явления. В том числе он должен распространяться и на электромагнитные явления, описываемые уравнениями Максвелла, которые выведены из эмпирически выявленных закономерностей. Однако, согласно последним, скорость распространения света является определённой величиной, не зависящей от скорости источника (по крайней мере в одной системе отсчёта). Из принципа относительности следует, что она не должна зависеть от скорости источника во всех ИСО в силу их равноправности. А значит, она должна быть постоянной во всех ИСО. В этом заключается суть второго постулата:
Постулат 2 (принцип постоянства скорости света). Скорость света в вакууме одинакова во всех системах координат, движущихся прямолинейно и равномерно друг относительно друга[8].
Принцип постоянства скорости света противоречит классической механике, а конкретно — закону сложения скоростей. При выводе последнего используется только принцип относительности Галилея и неявное допущение одинаковости времени во всех ИСО. Таким образом, из справедливости второго постулата следует, что время должно быть относительным — неодинаковым в разных ИСО. Необходимым образом отсюда следует и то, что «расстояния» также должны быть относительны. В самом деле, если свет проходит расстояние между двумя точками за некоторое время, а в другой системе — за другое время и притом с той же скоростью, то отсюда следует, что и расстояние в этой системе должно отличаться.
Световые сигналы не требуются при обосновании СТО. Хотя неинвариантность уравнений Максвелла относительно преобразований Галилея привела к построению СТО, последняя имеет более общий характер и применима ко всем видам взаимодействий и физических процессов. Фундаментальная константа , возникающая в преобразованиях Лоренца, имеет смысл предельной скорости движения материальных тел. Численно она совпадает со скоростью света, однако этот факт, согласно современной квантовой теории поля (уравнения которой изначально строятся как релятивистски инвариантные) связан с безмассовостью электромагнитного поля (фотона). Даже если бы фотон имел отличную от нуля массу, преобразования Лоренца от этого бы не изменились. Поэтому имеет смысл различать фундаментальную константу — скорость и скорость света [9]. Первая константа отражает общие свойства пространства и времени, тогда как вторая связана со свойствами конкретного взаимодействия.
Также используется постулат причинности: любое событие может оказывать влияние только на события, происходящие позже него, и не может оказывать влияние на события, произошедшие раньше него[10][11][12]. Из постулата причинности и независимости скорости света от выбора системы отсчёта следует, что скорость любого сигнала не может превышать скорость света[13][14][12].
Альтернативные аксиоматики[править | править код]
После построения Эйнштейном СТО на основе вышеуказанных постулатов многие исследователи пытались отказаться от второго постулата вообще. Спустя 5 лет после известной статьи Эйнштейна 1905 года, благодаря работам Игнатовского[15], Ф.Франка и Г.Роте[16] (см. исторический очерк) стал известен способ получения общего вида (с точностью до неопределённой константы) преобразований Лоренца без использования второго постулата. При «правильном» знаке неопределённого параметра эти преобразования совпадают с преобразованиями Лоренца. Из этого следует наличие максимальной скорости, одинаковой во всех ИСО. Тем не менее, знак этой константы из предложенных аксиом никак не следует. Предлагается оценивать значение параметра экспериментально. Чтобы измерить этот параметр, а значит, и фундаментальную скорость , нет необходимости проводить электродинамические эксперименты. Можно, например, на основе измерений скорости одного и того же объекта в разных ИСО воспользоваться законом сложения скоростей с неопределённым параметром[17]. Экспериментальное «вычисление» знака неопределённой константы фактически эквивалентно предположению о наличии максимальной скорости, то есть по существу второму постулату.
Тем не менее, попытки аксиоматизации, в том числе без второго постулата, предпринимались позднее и другими исследователями. Существуют также аксиоматики, которые не используют принцип относительности — а только принцип постоянства скорости света. Более подробно с ними можно ознакомиться в статье А. К. Гуца[18].
Преобразования Лоренца[править | править код]
Пусть координатные оси двух инерциальных систем отсчёта и параллельны друг другу, — время и координаты некоторого события, наблюдаемого в системе отсчёта , а — время и координаты того же события в системе .
Общий вид преобразований Лоренца в векторном виде[19], когда скорость систем отсчёта имеет произвольное направление:
где — фактор Лоренца, и — радиус-векторы события в системе и .
Если сориентировать координатные оси по направлению относительного движения инерциальных систем (то есть в общие формулы подставить ) и выбрать это направление в качестве оси (то есть так, чтобы система двигалась равномерно и прямолинейно со скоростью относительно вдоль оси ), то преобразования Лоренца примут следующий вид:
где — скорость света. При скоростях много меньше скорости света () преобразования Лоренца переходят в преобразования Галилея:
Подобный предельный переход является отражением принципа соответствия, согласно которому более общая теория (СТО) имеет своим предельным случаем менее общую теорию (в данном случае — классическую механику).
Вывод преобразований Лоренца[править | править код]
Существует множество способов вывода преобразований Лоренца. Рассмотрим один из вариантов.
Пусть начало координат системы (в силу однородности пространства это может быть любая покоящаяся в этой системе точка) движется относительно системы со скоростью . Соответственно, начало координат (покоящаяся точка) системы движется в со скоростью . В целях упрощения изложения будем предполагать совпадение начал отсчёта обеих ИСО (, когда ) и одинаковой ориентированности координатных осей. Пусть скорость системы () направлена по оси (против оси ).
При относительном движении систем вдоль оси x можно считать, что . Будем исследовать преобразования для одномерного пространства и рассматривать векторы двумерного пространства — времени .
Линейность преобразований[править | править код]
В силу однородности пространства и времени, изотропности пространства и принципа относительности преобразования от одной ИСО к другой должны быть линейными[20][21]. Линейность преобразований можно также вывести, предполагая, что если два объекта имеют одинаковые скорости относительно одной ИСО, то их скорости будут равны и в любой другой ИСО[22], (при этом необходимо использовать также слабые предположения о дифференцируемости и взаимной однозначности функций преобразования). Если использовать только «определение» ИСО: если некоторое тело имеет постоянную скорость относительно одной инерциальной системы отсчёта, то его скорость будет постоянна и относительно любой другой ИСО, то можно показать только, что преобразования между двумя ИСО должны быть дробно-линейными функциями координат и времени с одинаковым знаменателем[16][23].
Таким образом, если — пространственно-временной вектор в системе , то будем предполагать, что , где— матрица искомого линейного преобразования, зависящая только от относительной скорости рассматриваемых ИСО, то есть . Тогда линейное преобразование и закон сложения скоростей имеют следующий общий вид (структуру):
Рассмотрим движение точки из начала координат относительно системы с постоянной скоростью . Тогда для компонент столбцов и матрицы линейного преобразования выполнены равенства:
Подставив из второго равенства в первое, получим закон сложения скоростей в следующем виде:
По определению начало координат системы отсчёта движется относительно системы со скоростью , а значит, начало координат системы отсчёта движется относительно со скоростью ; если , то , а если , то . Учитывая это, получим
- .
Обозначив , получим
- .
Введём также обозначение . Отсюда получаем вид преобразования
- ,
и закона сложения скоростей
Отметим, что если дополнительно предположить , то можно сразу получить классический закон сложения скоростей и преобразования Галилея. Однако это предположение противоречит второму постулату.
Уже на этой стадии можно получить окончательный вид функции , используя второй постулат.
Другой способ состоит в рассмотрении свойств матрицы преобразования, которые следуют из принципа относительности и изотропности пространства. Эти свойства позволяют получить окончательный вид обеих функций и [22][24]. Далее приводится этот способ.
Свойства матрицы преобразования[править | править код]
Очевидно, если , то . Поскольку преобразования должны быть одинаковыми для всех ИСО (принцип относительности), то , так как если система движется относительно со скоростью , то это означает, что система движется относительно со скоростью . Таким образом
Подставив в это соотношение общий вид искомой матрицы , получим
где — нечётная функция.
В самом деле:
Поскольку левая часть есть единичная матрица, то из этого следует, что (нечётность) и . Следовательно
В силу изотропности пространства, смена координатных осей в противоположную сторону не должна влиять на вид зависимости между координатами в разных системах.
Выбрав произвольный вектор , в другой системе отсчёта получим . Поменяв координатную ось на противоположную в обеих системах, получим . В силу изотропности пространства, изменение направления не изменяет зависимость между координатами. Поэтому — чётная функция. Следовательно, . Поскольку при преобразование должно быть тождественным, то . В силу чётности вещественная функция неотрицательна в окрестности точки (границы окрестности определяются из равенства ). Следовательно, при взятии квадратного корня необходимо использовать только положительный знак: .
Тем самым остаётся только уточнить функцию . Это можно сделать сразу, воспользовавшись вторым постулатом. Однако из принципа относительности следует, что эта функция должна иметь вид , где — параметр, не зависящий от .
В самом деле, из принципа относительности следует, что преобразование координат от системы к системе , а затем к эквивалентно преобразованию от непосредственно к , причем законы преобразования одинаковы и зависят только от относительных скоростей этих систем. То есть
Подставим в это выражение полученный вид матрицы A:
Учитывая, что в первой матрице диагональные элементы одинаковы, то они должны быть одинаковы и в последней матрице, откуда следует, что . Следовательно,
для произвольных скоростей и . Это означает, что — постоянная величина, не зависящая от скорости .
Следовательно, матрица преобразования и закон сложения скоростей имеют следующий вид (с точностью до неопределённого параметра ):
- и закон сложения скоростей
Численное значение параметра и её знак невозможно вывести из вышеуказанных предположений[25]. Для этого необходимо либо дополнительное предположение (из которого будет следовать знак ), либо обращение к эксперименту (последнее необходимо в любом случае для установления конкретного значения ). Если , то получим классические преобразования Галилея; если , то получаем искомые преобразования Лоренца (введя обозначение ). Из дальнейшего будет ясно, что в этом случае константа имеет смысл максимальной скорости движения любого объекта.
Использование второго постулата[править | править код]
Из второго постулата и закона сложения скоростей следует, что и если , то .
Согласно второму постулату если , то . Поэтому из закона сложения скоростей следует, что , следовательно:
Откуда, .
Подставляя значения , получим
- ,
то есть зависит от скорости , что противоречит доказанной в предыдущем пункте независимости параметра от скорости.
Следовательно, если свет распространяется в направлении оси относительно системы отсчёта , движущейся относительно системы по оси , то и относительно системы отсчёта по оси свет распространяется в том же направлении.
Таким образом, окончательно получаем матрицу преобразования координатно-временного вектора и формулу преобразования скорости (закон сложения скоростей) при переходе от системы отсчёта к системе :
- ,
Для получения обратных преобразований (от к ) достаточно вместо скорости подставить и поменять местами и .
Интервал[править | править код]
Интервалом между произвольными событиями называется квадратный корень следующей величины:
где — являются разностями времён и координат двух событий.
Непосредственной подстановкой преобразований Лоренца можно убедиться, что интервал оказывается одинаковым во всех ИСО. Этот факт, однако, можно показать и без использования полученных преобразований Лоренца, а используя только постулаты СТО[26] (включая однородность и изотропность пространства и однородность времени).
Если интервал между событиями равен нулю в одной ИСО, то это означает, что период времени — это время (в данной ИСО) прохождения световым сигналом пути между пространственными координатами данных точек. В другой ИСО он проходит путь между этими точками (длина этого пути равна ) за некоторый другой период времени , поэтому скорость, умноженная на также должна быть равна . Однако согласно второму постулату скорость светового сигнала одинакова во всех ИСО, поэтому и во второй ИСО интервал будет равен нулю. Таким образом, непосредственно из второго постулата следует утверждение:
- если то и в любой другой ИСО
Для бесконечно близких событий имеем и Пусть В частности, если то и В силу однородности пространства и времени не может зависеть от пространственно-временных координат, а может зависеть только от относительной скорости систем отсчёта. Она не должна также зависеть от направления относительного движения в силу изотропности пространства. В силу принципа относительности функция зависимости от относительной скорости должна быть универсальной, то есть одинаковой для всех ИСО. Рассмотрим три системы отсчёта , где векторы скорости движения и в системе равны и Рассмотрим некоторый интервал в этих трёх системах отсчёта:
Отсюда Однако зависит не только и но и от направления этих векторов, поэтому это соотношение возможно, только если функция от вообще не зависит, то есть является некоторой константой. Из этого же соотношения следует, что a = 1. Это означает, что всегда выполнено соотношение
Отсюда следует, что — значение интервала во всех ИСО одинаково, то есть интервал является инвариантом при переходе от одной ИСО к другой.
Если , то говорят, что события разделены времениподобным интервалом; если , то пространственноподобным интервалом. Наконец, если то такие интервалы называются светоподобными.
Инвариантность интервала означает, что он имеет одинаковое значение в любых инерциальных системах отсчёта:
Про события, интервал между которыми времениподобен или светоподобен, всегда можно сказать, что одно событие произошло до другого (то есть эти события можно упорядочить во времени, и их последовательность будет одинаковой в любой ИСО). Эти события могут быть связаны причинно-следственными связями.
В событиях, интервал между которыми пространственноподобен, нет определённой последовательности: если в одной системе отсчёта два события произошли в моменты времени то можно найти другую инерциальную систему отсчёта (двигающуюся относительно первой с определённой скоростью ), в которой события произошли в моменты времени в другом порядке: Такие события не могут быть связаны причинно-следственными связями.
Светоподобный интервал соответствует событиям, которые могут быть связаны сигналом, распространяющимся со скоростью света. Уравнение для светоподобного интервала записанное в виде задаёт конус, называемый световым конусом данного события; на световом конусе находятся все точки в прошлом и будущем, которые можно связать световым сигналом с данным событием.
Перечисленные свойства можно вывести из преобразований Лоренца, если записать их в виде:
Знак интервала, вообще говоря, можно выбрать произвольно. В первоначальной версии интервал записывался с обратным знаком (то есть пространственные координаты со знаком «+», а временная — «−»). В современной литературе чаще используют вышеприведённую формулу.
Сами преобразования Лоренца можно получить из их линейности и требования инвариантности интервала.
Рассмотрим для простоты также случай одномерного пространства. Инвариантность интервала означает, что Подставим в это выражение линейные преобразования:
Получим
Поскольку и произвольны, то коэффициенты левой и правой частей должны быть тождественно равны. Следовательно,
Из последнего равенства следует, что Обозначим указанное отношение Кроме этого, обозначим Тогда и первые два соотношения можно записать как
Отсюда следует, что, во-первых, во-вторых, откуда можно записать Наконец, введя для удобства обозначение получим:
причём знаки в матрице либо положительные, либо отрицательные одновременно. Знак в формуле для необходимо выбрать положительный, поскольку при нулевой относительной скорости систем матрица A должна быть единичной (системы в этом случае идентичны и преобразования тождественные). Но если бы коэффициент в γ был бы отрицательным, это было бы невозможно (верхний диагональный элемент был бы равен −1, а должен быть равен +1). Поэтому однозначно можно утверждать, что — положительное число.
Что касается знаков внутри матрицы и собственно значения то их можно установить, если взять начало координат системы — вектор — и преобразовать его к системе и использовать соглашение о скорости движения :
Разделив первое уравнение этой системы на второе, получим Что касается знака, то ввиду положительности времени из второго уравнения следует, что знак должен быть положительным. Таким образом, окончательно имеем:
Геометрический подход[править | править код]
Четырёхмерное пространство-время[править | править код]

По своей форме интервал (особенно в первоначальной записи) напоминает расстояние в евклидовом пространстве, однако он имеет различный знак у пространственных и временных составляющих события. Следуя Минковскому и более ранней работе Пуанкаре, можно постулировать существование единого метрического четырёхмерного пространства-времени с 4-координатами . В простейшем случае плоского пространства метрика, определяющая расстояние между двумя бесконечно близкими точками, может быть евклидовой или псевдоевклидовой. Последний случай соответствует специальной теории относительности. Говорят, что интервал задаёт расстояние в псевдоевклидовом четырёхмерном пространстве-времени. Его также называют пространством-временем Минковского.
Наиболее «простой» способ понимания и вывода преобразований Лоренца при таком подходе может быть получен, если записать интервал (с обратным знаком), используя «мнимую» координату времени :
Тогда интервал выглядит как обычное евклидово расстояние между точками в четырёхмерном пространстве. Как было показано, интервал должен сохраняться при переходе между ИСО, следовательно, это могут быть либо параллельные переносы и инверсии (что не интересно), либо повороты в этом пространстве. Преобразования Лоренца играют роль поворотов в таком пространстве. Вращения базиса в четырёхмерном пространстве-времени, смешивающие временную и пространственные координаты 4-векторов, выглядят как переход в движущуюся систему отсчёта и похожи на вращения в обычном трёхмерном пространстве. При этом естественно изменяются проекции четырёхмерных интервалов между определёнными событиями на временную и пространственные оси системы отсчёта, что и порождает релятивистские эффекты изменения временных и пространственных интервалов. Именно инвариантная структура этого пространства, задаваемая постулатами СТО, не меняется при переходе от одной инерциальной системы отсчёта к другой. Используя только две пространственные координаты (x, y), четырёхмерное пространство можно изобразить в координатах (t, x, y). События, связанные с событием начала координат (t=0, x=y=0) световым сигналом (светоподобный интервал), лежат на так называемом световом конусе (см. рисунок справа).
В первоначальной версии Минковского (с мнимым временем) формулы преобразований Лоренца выводятся довольно просто — они следуют из известных формул поворотов в евклидовом пространстве.
Для этого достаточно понять, что тангенс угла между лучом, исходящим из начала координат (изображающий равномерное и прямолинейное движение), и осью равен:
Уже из этого можно вывести закон сложения скоростей, используя формулу тангенса суммы углов (тангенс угла между двумя лучами, выражающими движения с некоторыми скоростями в данной системе, и выражает их относительную скорость движения). Если угол между системами равен , а угол между лучом движущегося тела и лучом системы равен , тогда для скорости тела u относительно системы S имеем:
Сократив , получим закон сложения скоростей (заметим, что без i - в знаменателе получился бы "-").
Также несложно вывести выражения для косинуса и синуса угла:
Учитывая общую формулу поворотов в плоскости в евклидовом пространстве, получим:
Разделив последнее на , получим
Однако современный подход заключается во введении четырёхмерного пространства-времени (с вещественной осью времени ) с псевдометрикой. В таком пространстве формулы поворотов имеют аналогичный вид, однако вместо тригонометрических функций нужно использовать гиперболические.
В таком пространстве . Закон сложения скоростей:
Сократив скорость света, получим искомый закон сложения скоростей.
Повороты в этом пространстве в плоскости описываются следующим образом
Учитывая, что и , получим искомые преобразования Лоренца.
Геометрический подход Минковского и Пуанкаре был развит в 1914 году А. Роббом, который положил в основу аксиоматического построения СТО понятие о следовании событий. Данный подход был в дальнейшем развит А. Д. Александровым в работах 50-х—70-х годов. Базовая аксиоматика предполагает[18], что пространство-время является, во-первых, четырёхмерным связным односвязным локально-компактным хаусдорфовым топологическим пространством с определённой на нём группой параллельных переносов (формально — транзитивной коммутативной группой гомеоморфизмов пространства на себя). Это означает, что оно является аффинным пространством с этой группой переносов. Во-вторых — и это самый принципиальный момент — каждой точке пространства-времени сопоставлены подмножества (содержащие, кроме этой точки, также и другие) так называемые «области воздействия» (или следования, последующих событий) точки — такие, что для любой другой точки области воздействия её область воздействия входит в область воздействия данной точки. Данное предположение вводит отношение частичного порядка в пространстве времени — отношение следования или причинности. Данное отношение позволяет ввести понятие ограниченного множества (в смысле этого отношения порядка). Формально-математическим аналогом второго постулата СТО (ограниченности скорости передачи воздействия) в данном случае будет предположение об ограниченности пересечения «последующего» множества данной точки и «предшествующего» множества любой «последующей» точки. Эти предположения являются базовыми. Тем не менее, этих предположений оказывается недостаточно для получения преобразований Лоренца. Приходится делать дополнительные предположения о существовании группы взаимно-однозначных отображений, обладающих определёнными свойствами по отношению к «областям воздействия». Вместе с этими дополнительными аксиомами указанная группа отображений фактически является группой Лоренца и тем самым могут быть введены декартовы координаты, псевдометрика и собственно явный вид преобразований Лоренца.
Геометрическая интерпретация пространства-времени позволяет формулировать СТО в ковариантной форме (см. ниже) на основе тензорного анализа. Именно геометрическая интерпретация является основой для обобщения теории относительности (общая теория относительности).
Пространство скоростей[править | править код]
Возможен ещё один подход, в котором постулируется геометрическая структура пространства скоростей. Каждая точка такого пространства соответствует некоторой инерциальной системе отсчёта, а расстояние между двумя точками — модулю относительной скорости между ИСО. В силу принципа относительности все точки такого пространства должны быть равноправными, а, следовательно, пространство скоростей является однородным и изотропным. Если его свойства задаются римановой геометрией, то существует три и только три возможности: плоское пространство, пространство постоянной положительной и отрицательной кривизны. Первый случай соответствует классическому правилу сложения скоростей. Пространство постоянной отрицательной кривизны (пространство Лобачевского) соответствует релятивистскому правилу сложения скоростей и специальной теории относительности.
Групповой подход[править | править код]
Преобразования от одной системы отсчёта к другой можно построить на аксиоматической основе, без уточнения структуры пространства-времени[18]. Для этого вводят понятие множества «событий» . Инерциальные системы отсчёта представляют собой некоторые отображения (взаимно-однозначные) «событий» в — в четырёхмерное арифметическое пространство. Первые три числа — пространственные компоненты, последняя — время. Среди подмножеств выделяются инерциальные движения , которые определяются как подмножества, которые отображаются (при отображении ) в векторы, пространственные компоненты которого связаны с временной следующим образом , где коэффициенты — константы. В частности, если все , то имеем покоящееся «инерциальное движение» (покоящееся тело). Собственно сами преобразования от системы к представляют собой композицию .
Далее необходимо формализовать понятие движения одной ИСО относительно другой. Говорят, что покоится относительно S, если «покоящееся тело» в также покоится и в . В противном случае говорят, что движется относительно . В первую очередь предполагается, что существуют ИСО, движущиеся относительно друг друга (аксиома 1).
Далее определим линейное преобразование в , пространственная часть матрицы которой представляет собой ортогональное преобразование, а из временной (четвёртая строка и четвёртый столбец) диагональный элемент равен 1, остальные нулю. Назовём это преобразование «пространственным поворотом» (чем он по сути и является). Предполагается (аксиома 2а), что для всякой системы отсчёта существует система , преобразование к которой представляет собой некоторый пространственный поворот , в частности (аксиома 2б), если покоится относительно некоторой системы , то соответствующее преобразование является некоторым пространственным поворотом. Кроме этого, предполагается (аксиома 3), что для всякого инерциального движения существует другое инерциальное движение , которое отображается в данной системе отсчёта одинаково с точностью до некоторого пространственного поворота.
Наконец ещё одно предположение (аксиома 4) заключается в том, что для всякого преобразования между некоторыми инерциальными системами и для произвольной системы найдётся такая система отсчёта , что преобразование от к тождественно преобразованию .
Оказывается, такая система аксиом приводит к тому что группа преобразований может быть либо галилеевой, либо имеет вещественный параметр , что совпадает с неоднородной группой Лоренца.
Следствия преобразований Лоренца[править | править код]
Сложение скоростей[править | править код]
Непосредственным следствием преобразований Лоренца является релятивистское правило сложения скоростей. Если некоторый объект имеет компоненты скорости относительно системы и — относительно , то они связаны равенствами:
Повороты в пространстве-времени с вещественной осью ct плоскости описываются так
Учитывая, что и и
получим
Умножая на скорость света, получим закон сложения скоростей.
В этих соотношениях относительная скорость движения системы отсчёта направлена вдоль оси .
Если объект движется со скоростью света вдоль оси x относительно системы , то такая же скорость у него будет и относительно : . Это означает, что скорость является инвариантной (одинаковой) во всех ИСО.
Релятивистское сложение скоростей, как и преобразования Лоренца, при малых скоростях () переходит в классический закон сложения скоростей.
Замедление времени[править | править код]
Если часы неподвижны в системе , то для двух последовательных событий, фиксируемых в некоторой точке системы , имеет место . Из преобразования Лоренца следует, что такие часы перемещаются относительно системы по закону . Поэтому из преобразования для интервалов времени, измеряемых наблюдателями в системах и , следует соотношение
В этой формуле интервал времени (интервал собственного времени) измеряется часами, покоящимися в системе , которая движется относительно системы . Он сравнивается с интервалом нескольких различных, синхронно идущих часов, расположенных в системе . Поскольку при , то это означает, что часы в системе отсчёта , движущиеся относительно системы со скоростью , идут медленнее часов в . С этим эффектом связан так называемый парадокс близнецов.
Если часы движутся с переменной скоростью относительно инерциальной системы отсчёта, то время, измеряемое ими в сопутствующей системе отсчёта, где часы покоятся (собственное время), может быть вычислено по формуле:
где суммируются интервалы времени в локально инерциальных системах отсчёта.
Относительность одновременности[править | править код]
Если два разнесённых в пространстве события (например, вспышки света) происходят одновременно в движущейся со скоростью системе отсчёта , то они будут неодновременными относительно «неподвижной» системы . При из преобразований Лоренца следует
Если , то и . Это означает что, с точки зрения неподвижного наблюдателя в системе , левое событие в точке происходит раньше правого в точке . Относительность одновременности приводит к невозможности синхронизации часов в различных инерциальных системах отсчёта во всём пространстве.
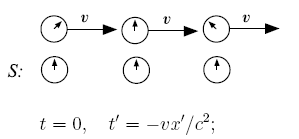
Пусть в каждой из систем отсчёта и вдоль осей и расположены синхронизированные между собой часы, и пусть «центральные» часы в момент, когда они находятся напротив друг друга, имеют координаты и показывают одинаковое время (левый и правый рисунки). В этот момент с точки зрения наблюдателя в системе (левый рисунок), часы в движущейся системе отсчёта не синхронизированы: они показывают различное время. Часы в , находящиеся от «центральных» по ходу движения системы (), отстают от них (), а часы, находящиеся от «центральных» против хода движения (), опережают «центральные» часы. И чем часы в дальше от «центральных» по ходу движения, тем больше они отстают от «центральных» (опережают «центральные», если находятся от них против движения).
Аналогичная ситуация для наблюдателей в системе (правый рисунок).
Сокращение линейных размеров[править | править код]
Если размеры движущегося вместе с системой объекта определять в неподвижной системе отсчёта при помощи одновременной фиксации координат его границ, то из преобразования Лоренца следует, что длина тела , измеренная в системе отсчёта , сокращается вдоль направления его движения по сравнению с длиной , измеренной в том же направлении в системе отсчёта , связанной с телом (собственной длиной тела):
В неподвижной системы отсчёта сокращаются все размеры вдоль направления движения тел, движущихся вместе с системой отсчёта — как самих тел, так и пустоты между ними. Поперечные размеры не изменяются.
Продольное сокращение размеров называют лоренцевым сокращением. Яркий пример — парадокс шеста и сарая, где длинный шест в полёте за счёт укорочения длины помещается в более короткий сарай.
При визуальном наблюдении движущихся тел дополнительно к лоренцевому сокращению необходимо учитывать время распространения светового сигнала от поверхности тела. В результате быстро движущееся тело выглядит наклонённым, а не сжатым в направлении движения.
Эффект Доплера[править | править код]
Пусть источник, движущийся со скоростью , излучает электромагнитный сигнал, имеющий частоту , измеренную наблюдателем в системе отсчёта , связанной с источником (собственная частота). Если этот же сигнал регистрируется «неподвижным» наблюдателем в системе , то его частота будет отличаться от собственной частоты:
где — угол между направлением на источник и его скоростью.
Различают продольный и поперечный эффект Доплера. В первом случае , то есть источник и приёмник находятся на одной прямой. Если источник движется от приёмника, то его частота уменьшается (красное смещение), а если приближается, то частота увеличивается (синее смещение):
Поперечный эффект возникает, когда , то есть приёмник направлен перпендикулярно скорости источника (например, источник «пролетает над» приёмником). В этом случае , где интервалы и равны периоду колебаний в собственной системе отсчета и движущейся относительно неё системе отсчета . Эффект замедления хода часов проявляется в уменьшении частоты в системе отсчета по сравнению с собственной частотой :
Аналога поперечного эффекта в классической физике нет, и это чисто релятивистский эффект. В отличие от этого, продольный эффект Доплера обусловлен как релятивистским эффектом замедления времени, так и классической составляющей.
Аберрация[править | править код]
Аберрация света является видимым смещением объекта при относительном движении наблюдателя и этого объекта. Пусть в системе отсчёта источник света неподвижен, и находится под углом к оси . Тогда в системе , относительно которой система движется вдоль оси со скоростью , направление на этот источник света составит угол . В соответствии с релятивистским правилом сложения скоростей, эти два угла связаны следующим образом:
где .
Релятивистская динамика[править | править код]
Релятивистский лагранжиан[править | править код]
В классической механике законы движения можно вывести из вида лагранжиана механической системы на основе принципа наименьшего действия. Действие должно быть инвариантом относительно преобразований ИСО. Таким свойством обладает интервал. Следовательно, общий вид действия в релятивистской механике
Соответственно, лагранжиан должен быть равен:
Параметр необходимо определить из соображений совпадения (с точностью до константы) с лагранжианом свободной частицы классической механикой при малых скоростях (который равен просто кинетической энергии). Исходя из этого, можно показать, что лагранжиан свободной релятивистской частицы имеет вид:
На основе этого лагранжиана можно вывести динамику релятивистской частицы, исходя из классических определений понятий через лагранжиан и уравнений Эйлера-Лагранжа.
Энергия и импульс[править | править код]

Если частица с массой (покоя) движется со скоростью , то её энергия и импульс имеют следующую зависимость от скорости:
Эти соотношения обобщают классические выражения для энергии и импульса, которые получаются при разложении в ряд по :
При нулевой скорости энергия частицы называется энергией покоя: .
В современной физической литературе принято, что m — масса частицы — не зависит от скорости, являясь инвариантом относительно преобразований Лоренца, и является величиной неаддитивной (то есть масса тела, состоящего из нескольких частей, в отличие от классической механики, не равна сумме масс этих частей). Понятие «релятивистской массы», зависящей от скорости , не используется[27], хотя оно и встречается в ранних работах по теории относительности. Историческая причина введения этого понятия была связана с попытками сохранить для релятивистского импульса классическую форму: .
При приближении скорости тела к скорости света его энергия и импульс стремятся к бесконечности. Это одна из причин, по которой «обычные» объекты не способны двигаться быстрее скорости света. Для частицы с ненулевой массой даже достижение скорости света потребует затраты бесконечной энергии. Заметные отклонения от классических выражений для энергии и импульса происходят при скоростях, близких к скорости света. Если скорости относительно невелики, то отклонения от классической динамики незначительны. Например, при скорости относительная разница релятивистского и классического импульса составляет всего 3 %.
Между релятивистской энергией и импульсом существуют следующие связи:
Эти формулы остаются справедливыми и для объектов, движущихся со скоростью света. В этом случае их масса покоя должна быть равна нулю .
Преобразования энергии и импульса[править | править код]
Аналогично преобразованиям Лоренца для времени и координат релятивистские энергия и импульс, измеренные относительно различных инерциальных систем отсчёта, связаны аналогичными соотношениями:
где компоненты вектора импульса равны . Относительная скорость и ориентация инерциальных систем отсчёта S, S' определены так же, как и в преобразованиях Лоренца.
Уравнения движения[править | править код]
Действующая на тело сила изменяет его импульс. Поэтому второй закон Ньютона в форме
остаётся справедливым также и в теории относительности. Однако производная по времени берётся от релятивистского импульса, а не от классического. Это приводит к тому, что связь силы и ускорения существенно отличается от классической:
Первое слагаемое содержит «релятивистскую массу», равную отношению силы к ускорению, если сила действует перпендикулярно скорости. В ранних работах по теории относительности её называли «поперечной массой». Именно её «рост» наблюдается в экспериментах по отклонению электронов магнитным полем. Второе слагаемое содержит «продольную массу», равную отношению силы к ускорению, если сила действует параллельно скорости:
Как было отмечено выше, эти понятия являются устаревшими и связаны с попыткой сохранить классическое уравнение движения Ньютона .
Скорость изменения энергии равна скалярному произведению силы на скорость тела:
Это приводит к тому, что, как и в классической механике, составляющая силы, перпендикулярная к скорости частицы, не изменяет её энергию (например, магнитная составляющая в силе Лоренца).
Ковариантная формулировка[править | править код]
Метрический тензор[править | править код]
Расстояние между двумя бесконечно близкими событиями можно записать при помощи метрического тензора в тензорном виде:
где , а по повторяющимся индексам подразумевается суммирование от 0 до 3. В инерциальных системах отсчёта с декартовыми координатами метрический тензор имеет следующий вид:
Кратко эта диагональная матрица обозначается таким образом: .
Выбор недекартовой системы координат (например, переход к сферическим координатам) или рассмотрение неинерциальных систем отсчёта приводит к изменению значений компонент метрического тензора, однако его сигнатура остаётся неизменной. В рамках специальной теории относительности всегда существует глобальное преобразование координат и времени, которое делает метрический тензор диагональным с компонентами . Эта физическая ситуация соответствует переходу в инерциальную систему отсчёта с декартовыми координатами. Другими словами, четырёхмерное пространство-время специальной теории относительности является плоским (псевдоевклидовым). В отличие от этого, общая теория относительности (ОТО) рассматривает искривлённые пространства, в которых метрический тензор никаким преобразованием координат нельзя привести к псевдоевклидовому виду во всём пространстве, но сигнатура тензора сохраняется такой же.
4-вектор[править | править код]
Соотношения СТО могут быть записаны в тензорном виде при помощи введения вектора с четырьмя компонентами (цифра или индекс вверху компоненты является её номером, а не степенью!), которые при переходе от одной инерциальной системы к другой преобразуются аналогично преобразованиям Лоренца. Нулевую компоненту 4-вектора называют временно́й, а компоненты с индексами 1,2,3 — пространственными. Они соответствуют компонентам обычного трёхмерного вектора, поэтому 4-вектор обозначается также следующим образом: .
Компоненты 4-вектора, измеренные в двух инерциальных системах отсчёта, одна из которых движется со скоростью в направлении относительно второй, связаны друг с другом следующим образом:
Примерами 4-векторов являются:
4-координаты — точка в псевдоевклидовом пространстве-времени:
4-скорость:
4-импульс (энергия-импульс):
Аналогичным образом можно определить 4-ускорение: и 4-силу: .
При помощи метрического тензора можно ввести т. н. ковекторы, которые обозначаются той же буквой, но с нижним индексом:
Для диагонального метрического тензора с сигнатурой , ковектор отличается от 4-вектора знаком перед пространственными компонентами. Так, если , то .
Свёртка вектора и ковектора является инвариантом — имеет одинаковое значение во всех инерциальных системах отсчёта:
Для 4-координат инвариантом является интервал, для 4-скорости — квадрат скорости света, для 4-импульса (энергии-импульса) — это величина, пропорциональная квадрату массы (покоя):
Вводятся также 4-векторные дифференциальные операторы, например 4-градиент
Экспериментальные основания СТО[править | править код]
Теория относительности является логически непротиворечивой теорией[источник не указан 980 дней]. Это означает, что из её исходных положений нельзя логически вывести некоторое утверждение одновременно с его отрицанием. Поэтому множество так называемых парадоксов (подобных парадоксу близнецов) являются кажущимися. Они возникают в результате некорректного применения теории к тем или иным задачам, а не в силу логической противоречивости СТО.
Справедливость теории относительности, как и любой другой физической теории, в конечном счёте, проверяется эмпирически[28][29]. Экспериментальную проверку теории относительности существенно облегчает логическая эквивалентность двух постулатов СТО требованию лоренц-инвариантности физических законов в одной системе отсчёта[28].
Специальная теория относительности лежит в основе всей современной физики. Поэтому какого-либо отдельного эксперимента, «доказывающего» СТО, нет. Вся совокупность экспериментальных данных в физике высоких энергий, ядерной физике, спектроскопии, астрофизике, электродинамике и других областях физики согласуется с теорией относительности в пределах точности эксперимента. Например, в квантовой электродинамике (объединение СТО, квантовой теории и уравнений Максвелла) значение аномального магнитного момента электрона совпадает с теоретическим предсказанием с относительной точностью [30]. Фактически СТО является инженерной наукой. Её формулы используются при расчёте ускорителей элементарных частиц. Обработка огромных массивов данных по столкновению частиц, двигающихся с релятивистскими скоростями в электромагнитных полях, основана на законах релятивистской динамики, отклонения от которых обнаружено не было. Поправки, следующие из СТО и ОТО, используются в системах спутниковой навигации (GPS, ГЛОНАСС). СТО лежит в основе ядерной энергетики и т. д.
Всё это не означает, что СТО не имеет пределов применимости. Напротив, как и в любой другой теории, они существуют, и их выявление является важной задачей экспериментальной физики. Например, в теории гравитации Эйнштейна (ОТО) рассматривается обобщение псевдоевклидового пространства СТО на случай пространства-времени, обладающего кривизной, что позволяет объяснить большую часть астрофизических и космологических наблюдаемых данных. Существуют попытки обнаружить анизотропию пространства и другие эффекты, которые могут изменить соотношения СТО[31]. Однако необходимо понимать, что если они будут обнаружены, то приведут к более общим теориям, предельным случаем которых снова будет СТО. Точно так же при малых скоростях верной остаётся классическая механика, являющаяся частным случаем теории относительности. Вообще, в силу принципа соответствия, теория, получившая многочисленные экспериментальные подтверждения, не может оказаться неверной, хотя область её применимости может быть ограничена.
Ниже приведены только некоторые эксперименты, иллюстрирующие справедливость СТО и её отдельных положений.
Релятивистское замедление времени[править | править код]
Тот факт, что время движущихся объектов течёт медленнее, получает постоянное подтверждение в экспериментах, проводимых в физике высоких энергий. Например, время жизни мюонов в кольцевом ускорителе в CERN[32] с точностью увеличивается в соответствии с релятивистской формулой. В данном эксперименте скорость мюонов была равна 0,9994 от скорости света, в результате чего время их жизни увеличилось в 29 раз. Этот эксперимент важен также тем, что при 7-метровом радиусе кольца ускорение мюонов достигало значений от ускорения свободного падения. Это, в свою очередь, свидетельствует о том, что эффект замедления времени обусловлен только скоростью объекта и не зависит от его ускорения. В настоящее время (2017 год) экспериментальная проверка формулы релятивистского замедления времени осуществлена с точностью до нескольких миллиардных долей[33].
Измерение величины замедления времени проводилось также с макроскопическими объектами. Например, в эксперименте Хафеле — Китинга проводилось сравнение показаний неподвижных атомных часов и атомных часов, летавших на самолёте. Эффект релятивистского замедления времени учитывается в бортовых часах спутниковых навигационных систем (GPS-Navstar, «ГЛОНАСС», «Бэйдоу», «Галилео» и т. д.), поэтому корректная работа таких систем является его экспериментальным подтверждением.
Независимость скорости света от движения источника[править | править код]
На заре возникновения теории относительности определённую популярность получили идеи Вальтера Ритца о том, что отрицательный результат опыта Майкельсона может быть объяснён при помощи баллистической теории[21]. В этой теории предполагалось, что свет со скоростью излучается относительно источника, и происходит сложение скорости света и скорости источника в соответствии с классическим правилом сложения скоростей. Естественно, эта теория противоречит СТО.
Астрофизические наблюдения являются убедительным опровержением подобной идеи. Например, при наблюдении двойных звёзд, вращающихся относительно общего центра масс, в соответствии с теорией Ритца происходили бы эффекты, которые на самом деле не наблюдаются (аргумент де Ситтера). Действительно, скорость света («изображения») от звезды, приближающейся к Земле, была бы выше скорости света от удаляющейся при вращении звезды. При большом расстоянии от двойной системы более быстрое «изображение» существенно обогнало бы более медленное. В результате видимое движение двойных звёзд выглядело бы достаточно странным, что не наблюдается.
Иногда встречается возражение, что гипотеза Ритца «на самом деле» верна, но свет при движении сквозь межзвёздное пространство переизлучается атомами водорода, имеющими в среднем нулевую скорость относительно Земли, и достаточно быстро приобретает скорость .
Однако, если бы это было так, возникала бы существенная разница в изображении двойных звёзд в различных диапазонах спектра, так как эффект «увлечения» средой света существенно зависит от его частоты[34].
В опытах Томашека (1923 г.) при помощи интерферометра сравнивались интерференционные картины от земных и внеземных источников (Солнце, Луна, Юпитер, звёзды Сириус и Арктур). Все эти объекты имели различную скорость относительно Земли, однако смещения интерференционных полос, ожидаемых в модели Ритца, обнаружено не было. Эти эксперименты в дальнейшем неоднократно повторялись. Например, в эксперименте Бонч-Бруевича А. М. и Молчанова В. А. (1956 г.) измерялась скорость света от различных краёв вращающегося Солнца. Результаты этих экспериментов также противоречат гипотезе Ритца[35].
Независимость скорости света от скорости источника регистрируется и в наземных экспериментах. Например, проводилось измерение скорости пары фотонов, возникающих при аннигиляции электрона и позитрона, центр масс которых двигался со скоростью, равной половине скорости света. С экспериментальной точностью 10 % сложение скорости света и скорости источника обнаружено не было[36][37][38].
Исторический очерк[править | править код]
Связь с другими теориями[править | править код]
Гравитация[править | править код]
Закон всемирного тяготения Ньютона совместим с классической механикой, но несовместим со специальной теорией относительности. Так как со СТО несовместим закон Кулона (аналогичный закону тяготения Ньютона), но совместимы уравнения электромагнетизма Максвелла, то возникла идея поиска аналогичных уравнений гравитационного поля (гравитомагнетизм), отличающихся только знаками и постоянными множителями.
Возможно, одним из первых, кто подал идею об аналогии между гравитацией и уравнениями Максвелла, был Оливер Хевисайд в 1893 году[39][40][41].
На основе принципа относительности, Анри Пуанкаре (1905, 1906)[42][43], Рихард Ганс(1905)[44], Герман Минковский (1908)[45][46], Арнольд Зоммерфельд (1910)[47] и Хендрик Лоренц (1910)[48] опубликовали несколько вариантов видоизменённой теории гравитации Ньютона, совместимой со специальной теорией относительности. Для инвариантности относительно преобразований Лоренца скорость распространения гравитации была принята равной скорости света. Все эти теории оказались неудачными — в частности, отсутствовало уравнение гравитационного поля и предсказывалось недостаточное смещение перигелия Меркурия (примерно в 6 раз меньше, чем наблюдалось)[49][50].
В 1922 году Феликс Коттлер[51] вывел ряд соотношений лоренц-инвариантной теории гравитации через векторную и тензорную алгебру, получив полное выражение для гравитационной силы и гравитационного 4-потенциала.
Теория гравитации, математически повторяющая теорию электромагнетизма Максвелла, не является единственно возможной теорией гравитации, совместимой со СТО; существуют и другие лоренц-инвариантные теории[52]. К ним, в частности, относятся две теории Нордстрёма, созданные в 1912 и в 1913 годах, которые, однако, предсказывали не только неверную величину аномального смещения перигелия Меркурия, но даже неверный знак смещения[53].
Для описания гравитации Эйнштейн разработал расширение СТО (общую теорию относительности), в котором источником гравитации является кривизна пространства-времени. Тем не менее, динамика даже в рамках СТО может включать гравитационное взаимодействие, пока потенциал гравитационного поля много меньше .
Специальная теория относительности перестаёт работать в масштабах всей Вселенной, требуя замены на ОТО.
Классическая механика[править | править код]
Теория относительности входит в существенное противоречие с некоторыми аспектами классической механики. Например, парадокс Эренфеста показывает несовместимость СТО с понятием абсолютно твёрдого тела. Даже в классической физике предполагается: механическое воздействие на твёрдое тело распространяется со скоростью звука, а отнюдь не с бесконечной (как должно быть в воображаемой абсолютно твёрдой среде).
Квантовая механика[править | править код]
Специальная теория относительности (в отличие от общей) полностью совместима с квантовой механикой. Их синтезом является релятивистская квантовая теория поля. Однако обе теории вполне независимы друг от друга. Возможно построение как квантовой механики, основанной на нерелятивистском принципе относительности Галилея (см. уравнение Шрёдингера), так и теорий на основе СТО, полностью игнорирующих квантовые эффекты. Например, квантовая теория поля может быть сформулирована как нерелятивистская теория[54]. В то же время такое квантовомеханическое явление, как спин, последовательно не может быть описано без привлечения теории относительности (см. Уравнение Дирака).
Развитие квантовой теории всё ещё продолжается, и многие физики считают, что будущая теория всего ответит на все вопросы, имеющие физический смысл, и даст в пределах как СТО в сочетании с квантовой теорией поля, так и ОТО. Скорее всего, СТО ожидает такая же судьба, как и механику Ньютона — будут точно очерчены пределы её применимости. В то же время такая максимально общая теория пока является отдалённой перспективой.
Парадоксы специальной теории относительности[править | править код]
- Парадокс Белла: разорвётся ли струна, соединяющая релятивистские объекты?
- ГЗК-парадокс: наблюдаемые высокоэнергетичные космические лучи, похоже, нарушают предел Грайзена — Зацепина — Кузьмина, который является следствием СТО.
- Парадокс лестницы (или шеста и сарая): Может ли лестница за счёт релятивистского сокращения длины поместиться в меньший по размеру гараж?
- Парадокс близнецов: когда близнец-путешественник вернулся, он стал моложе или старше, чем его брат, который оставался на Земле?
- Парадокс субмарины: сила Архимеда на релятивистский объект (типа пули) изменяется при переходе от системы отсчёта, в которой покоится пуля, в систему отсчёта, в которой покоится жидкость.
- Парадокс Эренфеста о кинематике абсолютно твёрдого вращающегося диска.
См. также[править | править код]
Примечания[править | править код]
- Комментарии
- ↑ Впервые такие преобразования пространственно-временных координат получены В. Фогтом в 1887 году при исследовании эффекта Доплера (для света) как преобразования, сохраняющие уравнение колебаний упругой среды — светоносного эфира. Данная работа осталась незамеченной. Даже сам Фогт не использовал эти выводы в своей последующей статье того же года. Лоренц в 1892 и 1895 гг. формально вводит понятие «местное время», которое примерно сохраняет неизменными Уравнения Максвелла в движущейся системе отсчёта. В 1900 году Дж. Лармор в работе «Эфир и материя» опубликовал преобразования, сохраняющие уравнения Максвелла. Эти же преобразования уже в 1904 году переоткрыл Лоренц. «Преобразованиями Лоренца» их назвал впервые Пуанкаре, и это название закрепилось за ними.
- Источники
- ↑ Гинзбург В. Л. Как и кто создал теорию относительности? в Эйнштейновский сборник, 1974. — М.: Наука, 1976. — С. 351—385. — 400 с. — 9200 экз.
- ↑ Гинзбург В. Л. Как и кто создал теорию относительности? в Эйнштейновский сборник, 1966. — М.: Наука, 1966. — С. 366—378. — 375 с. — 16 000 экз.
- ↑ Сацункевич И. С. Экспериментальные корни специальной теории относительности. — 2-е изд. — М.: УРСС, 2003. — 176 с. — ISBN 5-354-00497-7.
- ↑ Мизнер Ч., Торн К., Уилер Дж. Гравитация. — М.: Мир, 1977. — Т. 1. — С. 109. — 474 с.
- ↑ Einstein A. Zur Elektrodynamik bewegter Korper — Ann Phys — 1905 — Bd 17 — S. 891.
перевод: Эйнштейн А. К электродинамике движущегося тела // Собрание научных трудов. — С. 7—35. - ↑ Киттель Ч., Наит У., Рудерман М. Берклеевский курс физики. — Издание 3-е, исправленное. — М.: Наука, 1986. — Т. I. Механика. — С. 373,374. — 481 с.
- ↑ Начала теоретической физики, 2007, с. 157.
- ↑ 1 2 Эволюция физики, 1948, с. 167.
- ↑ «Принцип параметрической неполноты» Архивная копия от 7 августа 2010 на Wayback Machine в книге «Релятивистский мир» Архивная копия от 23 августа 2021 на Wayback Machine
- ↑ Начала теоретической физики, 2007, с. 169.
- ↑ Неванлинна, 1966, с. 122.
- ↑ 1 2 Чудинов Э. М. Теория относительности и философия.— М.: Политиздат, 1974. — С. 222—227.
- ↑ Начала теоретической физики, 2007, с. 170.
- ↑ Неванлинна, 1966, с. 184.
- ↑ von W. v. Ignatowsky «Einige allgemeine Bemerkungen zum Relativitätsprinzip» Verh. d. Deutsch. Phys. Ges. 12, 788—96, 1910 (русский перевод Архивная копия от 2 июля 2017 на Wayback Machine)
- ↑ 1 2 von Philipp Frank und Hermann Rothe «Über die Transformation der Raumzeitkoordinaten von ruhenden auf bewegte Systeme» Ann. der Physik, Ser. 4, Vol. 34, No. 5, 1911, pp. 825—855 (русский перевод Архивная копия от 29 августа 2014 на Wayback Machine)
- ↑ Мермин Н. Д. Теория относительности без постулата о постоянстве скорости света // Физика за рубежом. Серия Б. (1986)
Перевод работы
Mermin N. D. Relativity without light // Am. J. Phys., Vol. 52, No. 2 (1984) p. 119—124. - ↑ 1 2 3 А. К. Гуц, «Аксиоматическая теория относительности», УМН, 37:2(224) (1982), с. 39—79.
- ↑ Паули В. Теория Относительности. — М.: Наука, Издание 3-е, исправленное. — С. 26. — 328 с. — 17 700 экз. — ISBN 5-02-014346-4.
- ↑ Матвеев А. Н. Механика и теория относительности. — Издание 2-е, переработанное. — М.: Высш. шк., 1986. — С. 78—80. — 320 с. — 28 000 экз.
- ↑ 1 2 Паули В. Теория Относительности. — М.: Наука, Издание 3-е, исправленное. — 328 с. — 17 700 экз. — ISBN 5-02-014346-4.
- ↑ 1 2 «Преобразования Лоренца» Архивная копия от 25 августа 2021 на Wayback Machine в книге «Релятивистский мир» Архивная копия от 23 августа 2021 на Wayback Machine.
- ↑ Фок В. А. Теория пространства времени и тяготения. — Издание 2-е, дополненное. — М.: Гос.изд. физ.-мат. лит., 1961. — С. 510—518. — 568 с. — 10 000 экз.
- ↑ Терлецкий Я. П. Парадоксы теории относительности. — М.: Наука, 1966. — С. 23—31. — 120 с. — 16 500 экз.
- ↑ Паули В. Теория Относительности. — М.: Наука, Издание 3-е, исправленное. — С. 27. — 328 с. — 17 700 экз. — ISBN 5-02-014346-4.
- ↑ Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.
- ↑ Окунь Л. Б. «Понятие массы», УФН, 1989, Выпуск 7. стр. 511—530. (статья Архивная копия от 7 сентября 2011 на Wayback Machine)
- ↑ 1 2 Анисович К. В. К экспериментальным основаниям специальной теории относительности // Эйнштейновский сборник 1973. — М., Наука, 1974. — c.360—395
- ↑ Вавилов С. И. Экспериментальные основания теории относительности // Собрание сочинений, т. 4. — М., АН СССР, 1956
- ↑ Бродский С., Дрелл С. Современный статус квантовой электродинамики. — УФН, 1972. — Т. 107, В.1. — С. 57—98.
- ↑ Эфир возвращается? Дата обращения: 18 декабря 2008. Архивировано 7 января 2008 года.
- ↑ Bailey J. et al. Measurements of relativistic time dilatation for positive and negative muons in a circular orbit (англ.) // Nature. — 1977. — Vol. 268. — Iss. 5618. — P. 301—305. — doi:10.1038/268301a0.
- ↑ Botermann B. et al. Test of Time Dilation Using Stored Li+ Ions as Clocks at Relativistic Speed (англ.) // Physical Review Letters. — 2014. — Vol. 113. — Iss. 12. — P. 120405. — doi:10.1103/PhysRevLett.113.120405. — arXiv:1409.7951.
- ↑ Сацункевич И. С. Экспериментальные корни специальной теории относительности. — 2-е изд. — М.: УРСС, 2003. — С. 128—130. — 176 с. — ISBN 5-354-00497-7.
- ↑ Сацункевич И. С. Экспериментальные корни специальной теории относительности. — 2-е изд. — М.: УРСС, 2003. — С. 122—123. — 176 с. — ISBN 5-354-00497-7.
- ↑ Sadeh D. Experimental Evidence for the Constancy of the Velocity of Gamma Rays, Using Annihilation in Flight. — Phys. Rev. Lett. 10, 1963. — P. 271—273.
- ↑ Сивухин Д. В. § 103. Независимость скорости света от движения источника // Общий курс физики. — М.: Наука, 1980. — Т. IV. Оптика. — 768 с.
- ↑ Франкфурт У. И., Френк А. М. глава: Независимость скорости света от скорости источника // Оптика движущихся тел. — М.: Наука, 1972.
- ↑ Oliver Heaviside. A Gravitational and Electromagnetic Analogy, Архивная копия от 2 июня 2021 на Wayback Machine Part I, The Electrician,31, 281—282 (1893).
- ↑ Oliver Heaviside. A Gravitational and Electromagnetic Analogy, Part II, The Electrician,31, 359 (1893).
- ↑ O. Heaviside, Electromagnetic Theory, The Electrician Printing and Publishing Co., London, 1894, Vol. I, Appendix B.
- ↑ Poincaré H. «Sur la dynamique de l’electron», Rendicenti del Circolo Matematico di Palermo, 1906, v.XXI, p. 129, Received for publication in July 23, 1905).
- ↑ Lorentz-Poincaré relativity and a scalar theory of gravitation. Дата обращения: 2 июня 2021. Архивировано 12 июля 2015 года.
- ↑ Gans, Richard. 1905. «Gravitation und Elektromagnetismus». Jahresbericht der deutschen Mathematiker-Vereinigung 14: 578—581.
- ↑ Minkowski, Hermann. 1908. «Die Grundgleichungen fur die electromagnetischen Vorgange in bewegten Korpern». Nachrichten von der Koniglichen Gesellschaft der Wissenschaften zu Gottingen, 53-111. (English translation of the appendix «Mechanics and the Relativity Postulate» in this volume.).
- ↑ Minkowski, Hermann. 1909. «Raum und Zeit». Jahresbericht der deutschen Mathematiker-Vereinigung 18: 75-88.
- ↑ Sommerfeld, Arnold. 1910. «Zur Relativitatstheorie, II: Vierdimensionale Vektoranalysis». Annalen der Physik 33: 649—689.
- ↑ Lorentz H.A. «Alte und neue Fragen der Physik», Physikalische Zeitschrift, 1910,11, 1234—1257.
- ↑ Визгин В. П., 1981, с. 60—63, 69—93.
- ↑ Walter, S. (2007). Renn, J. (ed.). "Breaking in the 4-vectors: the four-dimensional movement in gravitation, 1905–1910" (PDF). The Genesis of General Relativity. Berlin. 3: 193—252. Bibcode:2007ggr..conf..193W. Архивировано (PDF) из оригинала 2 июня 2021. Дата обращения: 2 июня 2021.
- ↑ Kottler, Felix. 1922. «Gravitation und Relativitatstheorie». In Karl Schwarzschild, Samuel Oppenheim, and Walther von Dyck (eds.), Astronomie, 2 vols, 2: 159—237. Encyklopadie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen 6. Leipzig: Teubner.
- ↑ Edward G. Harris. Class of Lorentz‐invariant theories of gravitation. American Journal of Physics 49, 1051 (1981); https://doi.org/10.1119/1.12581
- ↑ Визгин В. П., 1981, с. 166—189.
- ↑ Шварц А. С. Математические основы квантовой теории поля. М.: Атомиздат, 1975.
Литература[править | править код]
- Общее
- Визгин В. П. Релятивистская теория тяготения. Истоки и формирование. 1900—1915. — М. : Наука, 1981. — 352 с.
- Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.
- Паули В. Теория относительности. Изд. 2-е, испр. и доп. Перев. с нем. — М.: Наука, 1983. — 336 с.
- Спасский Б. И.. История физики. Том 2, часть 2-я. М.: Высшая школа, 1977.
- Уиттекер Э. История теории эфира и электричества. Современные теории 1900—1926. Пер с англ. Москва, Ижевск: ИКИ, 2004. 464с. ISBN 5-93972-304-7 (Глава 2)
- Работы основоположников
- Принцип относительности. Сб. работ по специальной теории относительности. М.: Атомиздат, 1973.
- Г. А. Лоренц. Интерференционный опыт Майкельсона. Из книги "Versucheiner Theoriederelektrischenundoptischen Erscheinungeninbewegten Korpern. Leiden, 1895, параграфы 89…92.
- Г. А. Лоренц.Электромагнитные явления в системе, движущейся с любой скоростью, меньшей скорости света. Proc Acad., Amsterdam, 1904, v 6, p. 809.
- А. Пуанкаре. Измерение времени. «Revuede Metaphysiqueetde Morale», 1898, t. 6, p. 1…13.
- А. Пуанкаре. Оптические явления в движущихся телах. ElectriciteetOptique, G. CarreetC. Naud, Paris, 1901, p. 535…536.
- А. Пуанкаре. О принципе относительности пространства и движения. Главы 5…7 из книги «Наука и гипотеза»(H. Poinrare. Scienceand Hypothesis. Paris, 1902.)
- А. Пуанкаре. Настоящее и будущее математической физики. Доклад, напечатанный в журнале «Bulletindes Sciences Mathematiques», 1904, v. 28, ser. 2, p. 302.
- А. Пуанкаре. О динамике электрона. Rendicontidel Circolo Matematicodi Palermo, 1906.
- А. Эйнштейн. К электродинамике движущихся тел. Ann. d. Phys.,1905 (рукопись поступила 30 июня 1905 г.), b. 17, s. 89.
- Эйнштейн А. Собрание научных трудов в четырёх томах. Том 1. Работы по теории относительности 1905—1920. М.: Наука, 1965.
- Эйнштейн А. Сущность теории относительности. — М.: Изд. ин. лит., 1955. — 157 с.
- А. Эйнштейн, Л. Инфельд. Эволюция физики. — М.: ОГИЗ, 1948. — 267 с.
- Дополнительная литература
- Угаров В. А. Специальная теория относительности. 2-е изд. М.: Наука, 1977.
- Тоннела М. А. Основы электромагнетизма и теории относительности. М.: ИЛ, 1962.
- Толмен Р. Относительность, термодинамика и космология. М.: Наука, 1974.
- Физическая энциклопедия, т.2 — М.: Большая Российская Энциклопедия. Физическая энциклопедия.
- Медведев Б. В. Начала теоретической физики. — М.: Физматлит, 2007. — 600 с.
- Неванлинна Р. Пространство, время и относительность. — М.: Мир, 1966. — 229 с.
Ссылки[править | править код]
- Релятивистский мир — лекции по теории относительности, гравитации и космологии
- Общая и специальная теория относительности на сайте «Мир математических уравнений» EqWorld
- Работы, описывающие структуру СТО и относительности синхронизации часов в ней: arxiv: gr-qc/0510024; arxiv: gr-qc/0510017; arxiv: gr-qc/0205039
- Статья о вкладе А. Пуанкаре в создание СТО: T. Damour: Poincare, Relativity, Billiards and Symmetry