Умножение
| Умножение | |
|---|---|
 | |
| Изображается на | знак умножения |
| Обозначение | знак умножения |
| Нейтральный элемент | 1 |
| Противоположно | деление |

Умноже́ние — одна из основных математических операций над двумя аргументами, которые называются множителями или сомножителями (иногда первый аргумент называют множимым, а второй множителем). Результат умножения называется их произведением[1].
Для натуральных чисел умножение определяется как многократное сложение[1] — чтобы умножить число на число , надо сложить чисел (умножение далее обозначено приподнятой точкой между сомножителями):
- .
Умножение для других типов чисел — целых, рациональных, вещественных, комплексных — определяется не через многократное сложение, а путём систематического обобщения.
Умножение чисел является коммутативной операцией, то есть порядок записи чисел-множителей не влияет на результат их умножения. Например, умножение чисел и может быть записано как , так и (произносится также «пятью три», «трижды пять»), и результатом в любом случае является число . Проверка через сложение:
- ,
- .
Умножение определяется не только для чисел, но и для различных нечисловых математических объектов[2] (например, матриц, векторов, множеств, кватернионов и т. д.), для каждого из которых имеет различный смысл, различные определения и свойства. Например, операция умножения для нечисловых объектов не всегда является коммутативной операцией.
При умножении физических величин важную роль играет их размерность, которая равноправно участвует в умножении.
Изучение общих свойств операции умножения входит в задачи общей алгебры, в частности теории групп и колец[2].
Формы записи и терминология[править | править код]
Умножение записывается с использованием знака умножения (∙, ×, ∗) между аргументами, такая форма записи называется инфиксной нотацией. В данном контексте знак умножения является бинарным оператором. Знак умножения не имеет специального названия, тогда как, например, знак сложения называется «плюс».
Самый старый из используемых символов — косой крестик (×). Впервые его использовал английский математик Уильям Отред в своём труде «Clavis Mathematicae» 1631 г. Немецкий математик Лейбниц предпочитал знак в виде приподнятой точки (∙). Этот символ он использовал в письме 1698 года. Йоханн Ран ввёл звёздочку (∗) в качестве знака умножения, она появилась в его книге «Teutsche Algebra» 1659 г.
В российских учебниках математики в основном используется знак в виде приподнятой точки (∙). Звёздочка (∗) используется, как правило, в текстах компьютерных программ.
Результат записывается с использованием знака равенства «», например:
- («шесть умножить на три равно восемнадцать» или «шестью три — восемнадцать»).
Часто в математических выражениях знак умножения опускается (не записывается), если это не вызывает неоднозначного прочтения. Например вместо пишется . Как правило, знак умножения опускают, если одним из множителей является однобуквенная переменная, функция или выражение в скобках: , , .
Традиционно при записи произведения нескольких множителей числа записывают перед переменными, а переменные перед функциями. Так, выражение будет записано как . Выражения в скобках традиционно записывают последними, то есть выражение будет записано как .
Свойства[править | править код]
Далее описаны основные свойства операции умножения на числовых множествах .
- Умножение коммутативно, то есть от перемены мест множителей произведение не меняется. Свойство также известно как переместительный закон умножения[3]:
- Умножение ассоциативно, то есть при последовательном выполнении умножения трёх или более чисел последовательность выполнения операций не имеет значения. Свойство также известно как сочетательный закон умножения[3]:
- Умножение дистрибутивно, это свойство согласованности двух бинарных операций, определённых на одном и том же множестве. Свойство также известно как распределительный закон[3]:
- Относительно умножения в множестве существует единственный нейтральный элемент — (число «один»). Умножение любого числа на (нейтральный элемент) даёт число, равное исходному:
- Умножение на идемпотентно, то есть повторное применение операции к объекту даёт тот же результат, что и одинарное:
- Умножение на (нулевой элемент) даёт (нуль):
- Нулевой элемент:
Операция умножения чисел, определённых на множествах , даёт произведение, принадлежащее этому же множеству. Следовательно, операция умножения относится к замкнутым операциям, то есть множества чисел образуют кольца относительно операции умножения.
На языке общей алгебры вышеперечисленные свойства сложения говорят о том, что являются абелевыми группами относительно операции умножения.
В математических выражениях операция умножения имеет более высокий приоритет по отношению к операциям сложения и вычитания, то есть она выполняется перед ними, но менее высокий приоритет, чем операция возведения в степень.
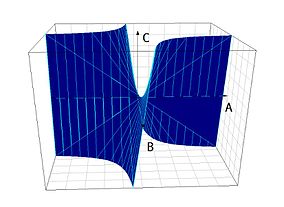
На множестве вещественных чисел область значений функции умножения графически имеет вид поверхности проходящей через начало координат и изогнутой с двух сторон в виде параболы.
Выполнение умножения[править | править код]
При практическом решении задачи умножения двух чисел необходимо свести её к последовательности более простых операций: «простое умножение», сложение, сравнение и др. Для этого разработаны различные методы умножения, например для чисел, дробей, векторов и др. На множестве натуральных чисел в настоящее время используется алгоритм поразрядного умножения. При этом следует рассматривать умножение как процедуру (в отличие от операции).
Процедура достаточно сложная, состоит из относительно большого числа шагов и при умножении больших чисел может занять продолжительное время.

«Простое умножение» в данном контексте обозначает операцию умножения одноразрядных чисел, которая может быть легко сведена к сложению. Является гипероператором сложения:
где — последовательное сложение элементов.
Чтобы упростить и ускорить процесс умножения используют табличный метод «простого умножения», для этого заранее вычисляют все комбинации произведений чисел от 0 до 9 и берут готовый результат из этой таблицы[4]:
| * | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 3 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| 4 | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
| 5 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 6 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
| 7 | 0 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
| 8 | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 |
| 9 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
Данная процедура применима к умножению натуральных и целых (с учётом знака) чисел. Для других чисел используются более сложные алгоритмы.
Умножение чисел[править | править код]
Натуральные числа[править | править код]
- Первый вариант определения
Умножением натуральных чисел называется такое соответствие, которое с каждой парой натуральных чисел и сопоставляет одно и только одно натуральное число , обладающее следующими свойствами[5]:
- 1)
- 2) .
- Второй вариант определения
Воспользуемся определением натуральных чисел как классов эквивалентности конечных множеств. Обозначим классы эквивалентности конечных множеств порождённых биекциями, с помощью скобок: . Тогда арифметическая операция «умножение» определяется следующим образом:
где: прямое произведение множеств — множество , элементами которого являются упорядоченные пары для всевозможных . Данная операция на классах введена корректно, то есть не зависит от выбора элементов классов, и совпадает с индуктивным определением.
Взаимно однозначное отображение конечного множества на отрезок можно понимать как нумерацию элементов множества .
Для умножения натуральных чисел в позиционной системе обозначения чисел применяется поразрядный алгоритм умножения. Если даны два натуральных числа и такие, что:
где ;
- — количество цифр в числе ;
- — порядковый номером разряда (позиции), ;
- — основание системы счисления;
- множество числовых знаков (цифр), конкретной системы счисления:
- ,
- ,
- ; тогда:
умножая поразрядно, получаем промежуточных результатов:
где: — значение переноса, — функция нахождения остатка от деления, — функция нахождения неполного частного.
Затем полученные промежуточных результатов складываем:
Таким образом операция умножения сводится к процедуре последовательного простого умножения одноразрядных чисел , с формированием переноса при необходимости, которое производится либо табличным методом, либо последовательным сложением. И далее к сложению.
Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и в десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами. При этом нужно пользоваться таблицей умножения, соответствующей данному основанию системы счисления.
Пример умножения натуральных чисел в двоичной, десятичной и шестнадцатеричной системах счисления, для удобства числа записываются друг под другом соответственно разрядам, перенос пишется сверху:
Целые числа[править | править код]
Множество целых чисел — расширение множества натуральных чисел , получаемое добавлением отрицательных чисел [6] вида . Множество целых чисел обозначается Арифметические операции над целыми числами определяются как непрерывное продолжение соответствующих операций над натуральными числами.

Отличие от натуральных чисел состоит в том, что отрицательные числа на числовой прямой направлены в противоположную сторону, это несколько меняет процедуру умножения. Необходимо учитывать взаимное направление чисел, здесь возможны несколько случаев:
- Если оба аргумента положительные, тогда:
- Если один из аргументов отрицателен, тогда: либо
- Если оба аргумента отрицательны, тогда:
Здесь и далее также используется алгоритм поразрядного умножения. Например, рассмотрим выражение: ; так как у чисел и разные знаки, то выносим минус за скобки: , вычисляя далее получим ответ: .
Рациональные числа[править | править код]
Множество рациональных чисел обозначается (от англ. quotient «частное») и может быть записано в таком виде:
Для умножения рациональных чисел в виде обыкновенных (или простых) дробей вида: , следует числители и знаменатели дробей умножить друг на друга.
Если даны два рациональных числа и такие, что: (дроби не сокращаемые), тогда[7]:
Пример умножения:
Арифметическая операция «умножение» над рациональными числами относится к замкнутым операциям.
Вещественные числа[править | править код]
Арифметические операции над вещественными числами представимых бесконечными десятичными дробями определяются как непрерывное продолжение[8] соответствующих операций над рациональными числами.
Если даны два вещественных числа, представимые бесконечными десятичными дробями:
определённые соответственно фундаментальными последовательностями рациональных чисел (удовлетворяющие условию Коши), обозначенные как: и , то их произведением называют число , определённое произведением последовательностей и :
вещественное число , удовлетворяет следующему условию:
Таким образом произведением двух вещественных чисел и является такое вещественное число которое содержится между всеми произведениями вида с одной стороны и всеми произведениями вида с другой стороны[9].
На практике для того, чтобы умножить два числа и , необходимо заменить их с требуемой точностью приближёнными рациональными числами и . За приближенное значение произведения чисел берут произведение указанных рациональных чисел . При этом не важно, с какой стороны (по недостатку или по избытку) взятые рациональные числа приближают и . Умножение производится по алгоритму поразрядного умножения.
Абсолютная погрешность произведения приближённых чисел: , абсолютная погрешность числа принимается равной половине последнего знака этого числа. Относительная погрешность произведения равна сумме относительных погрешностей аргументов: . Полученный результат округляют до первой верной значащей цифры, значащая цифра приближенного числа является верной, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.
Пример умножения , с точностью до 3-го знака после запятой:
- Округляем данные числа до 4-го знака после запятой (для повышения точности вычислений);
- Получаем: ;
- Поразрядно умножаем: ;
- Округляем до 3-го знака после запятой: .
График[править | править код]
На множестве пар вещественных чисел график функции умножения является проходящим через начало координат гиперболическим параболоидом.
Комплексные числа[править | править код]

Множество комплексных чисел с арифметическими операциями является полем и обычно обозначается символом .
Произведением двух комплексных чисел в алгебраической форме записи, называется комплексное число, равное:
где: , — мнимая единица.
Для того, чтобы перемножить два комплексных числа в тригонометрической форме записи, нужно перемножить их модули, а аргументы сложить:
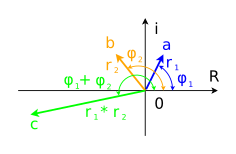
где: модуль и аргумент комплексного числа.
Умножение комплексного числа в показательной форме, на комплексное число сводится к повороту вектора, соответствующего числу , на угол и изменению его длины в раз. Для произведения комплексных чисел в показательной форме верно равенство:
где: — число e.
Экспоненциальная запись[править | править код]
В экспоненциальной записи числа записываются в виде , где — мантисса, — характеристика числа, — основание системы счисления, . Для умножения двух чисел, которые записаны в экспоненциальной форме необходимо умножить мантиссы и характеристики:
Например:
Умножение произвольных чисел[править | править код]
При умножении чисел, принадлежащих разным множествам, например , необходимо произвести преобразование (приведение) одного из множителей к типу второго (если существует такая возможность). Для этого число из множества с меньшей мощностью «расширяется» в сторону числа из множества с большей мощностью: . В данном примере следует воспользоваться тем, что натуральные числа являются подмножеством рациональных и трактовать натуральное число как рациональное число . Исходное выражение превращается в умножение двух рациональных чисел: .
Умножение физических величин[править | править код]
Единица измерения физической величины имеет определенное наименование (размерность), например, для длины — метр (м), для времени — секунда (с), для массы — грамм (г) и так далее. Результат измерения той или иной величины представляет собой не просто число, а число с размерностью[10], например, 10 м, 145 с, 500 г. Размерность представляет собой самостоятельный объект, который равноправно участвует в операции умножения. При умножении физических величин умножаются как сами числовые значения, так и их размерности, порождая новое число с новой размерностью. Например, прямоугольник со сторонами 5 м и 3 м обладает площадью, получаемой умножением длин сторон:
- 5 м · 3 м = 5 · 3 м·м= 15 м·м, или 15 м².
Таким образом, умножение физических величин надо рассматривать как нахождение новой физической величины, отличающейся от величин, которые мы умножаем. Если физически возможно создание такого произведения, например, при нахождении работы, скорости или других величин, то эта величина образует множество, отличное от начальных. В этом случае композиции этих величин присваивается новое обозначение (новый термин), например: плотность, ускорение, мощность и прочее[11].
Например, если умножить скорость равномерно и прямолинейно движущегося тела, равную 5 м/с, на время, равное 3 с, то получится именованное число (физическая величина), которая называется «длина», или «расстояние» и измеряется в метрах:
- 5 м/с · 3 с = 15 (м/с) · с = 15 м.
Помимо размерных физических величин существуют безразмерные величины. Безразмерные величины либо просто определяют некоторое количество (измеряются «штуками», «разами» и тому подобное), либо являются отношениями физических величин одной и той же размерности, например, относительная плотность является отношением плотности тела к эталонной плотности (обычно, плотности воды). При умножении величины с размерностью на безразмерную величину результат сохраняет исходную размерность. Например, если взять 5-метровые рейки в количестве 3 штуки, то в результате умножения получим общую длину реек 15 метров:
- 5 м · 3 = 15 м.
Количество реек (безразмерная величина) здесь не зависит ни от способа их подсчёта, ни от единицы измерения их длины. Например, если измерить длину не в метрах, а в футах, то длина той же рейки составит 16,4 фута, а общая длина трёх реек:
- 16,4 фута · 3 = 49,2 фута.
Умножение последовательностей[править | править код]
Произведение элементов последовательности может быть компактно записано с помощью специального символа умножения, восходящего к заглавной букве Π (пи) греческого алфавита, как показано в примере:
Снизу записывается символ свободной переменной (в данном случае ), называемой «индексом умножения», вместе с начальным значением (в данном случае 1). Сверху записывается конечное значение (в данном случае 4) в виде числа или переменной, либо символ бесконечности , если предполагается бесконечное произведение. Такую запись можно «развернуть» в выражение, в котором последовательно подставляются значения индекса умножения от начального до конечного значения:
где m и n есть целые числа или выражения, которые вычисляются в целочисленные значения.
Такая запись обладает следующим свойством[5]:104:
Если значения индекса заданы некоторым множеством, то многократное произведение может быть записано с его помощью, например
- .
Такая запись означает, что переменная «пробегает» все значения, принадлежащие множеству .
См. также[править | править код]
Примечания[править | править код]
- ↑ 1 2 Математическая энциклопедия, 1985.
- ↑ 1 2 Умножение // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- ↑ 1 2 3 Так это свойство обычно называется в школьных учебниках
- ↑ Истомина, 2005, с. 165.
- ↑ 1 2 Энциклопедия элементарной математики. Книга 1 (арифметика) Архивная копия от 17 декабря 2021 на Wayback Machine / Под ред. П. С. Александров, А. И. Маркушевич, А. Я. Хинчин. — М.-Л., ГТТИ, 1951. 448 с.
- ↑ Выгодский, 2003, с. 116—117.
- ↑ Гусев, 1988, с. 20.
- ↑ Поскольку на множестве вещественных чисел уже введено отношение линейного порядка, то мы можем определить топологию числовой прямой: в качестве открытых множеств возьмём всевозможные объединения интервалов вида
- ↑ Ильин, 1985, с. 46.
- ↑ Волинская Н. И. Интегрированный урок по физике и математике, Измерение физических величин и их единицы, СШ 7 г. Бреста. brestschool7.iatp.by. Дата обращения: 18 апреля 2016. Архивировано из оригинала 7 августа 2016 года.
- ↑ Макаров Владимир Петрович. О «размерности» физических величин. lithology.ru, Литология.РФ. Дата обращения: 18 апреля 2016. Архивировано 6 мая 2016 года.
Литература[править | править код]
- Барсуков А. Н. Алгебра. Учебник для 6-8 классов.. — Просвещение, 1966. — 296 с.
- Выгодский М. Я. Справочник по элементарной математике. — М.: АСТ, 2003. — ISBN 5-17-009554-6.
- Гусев В. А., Мордкович А. Г. Математика. Справочные материалы, книга для учащихся.. — Просвещение, 1988. — 416 с.
- Ильин В. А. и др. Математический анализ. Начальный курс.. — МГУ, 1985. — 662 с.
- Эндертон Г. Элементы теории множеств = Elements of Set Theory. — Gulf Professional Publishing, 1977. — 279 с. — ISBN 0-12-238440-7.
- Иванова О. А. Умножение чисел // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1985. — Т. 5. — С. 495—496. — 1248 с.
- Истомина Н. Б. Методика обучения математике в начальной школе: Развивающее обучение.. — Ассоциация XXI век, 2005. — 272 с. — ISBN 5-89308-193-5.












































![{\displaystyle [C],[A],[B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2b1513ee6a676b6711304946e6b007a239058aa)
![{\displaystyle [C]=[A]\cdot [B]=[A\times B];}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14f1d027d312b22fe9c0f0e7454dabce822ca53b)















































![{\displaystyle \alpha =[a_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c222a30a9a92c2e3eef762e7c2c43dceb2bb4d8c)
![{\displaystyle \beta =[b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a26985ffa366493195dac10ceda47058558cd721)
![{\displaystyle \gamma =[c_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34668f3552cf8e843401e133627da1ff0651fa03)


![{\displaystyle \gamma =\alpha \cdot \beta {\overset {\text{def}}{=}}[a_{n}]\cdot [b_{n}]=[a_{n}\times b_{n}];}](https://wikimedia.org/api/rest_v1/media/math/render/svg/747c6083d44ae3081ade2fcc5ac51517af1e9454)










































