Математика и изобразительное искусство: различия между версиями

Материал из Википедии — свободной энциклопедии
Перейти к навигации Перейти к поиску
Интерактивная навигация по истории
[отпатрулированная версия][отпатрулированная версия]
← Предыдущая правкаСледующая правка →
Содержимое удалено Содержимое добавлено
ВизуальныйВики-текст
Строка 137: Строка 137:


=== От математики к искусству ===
=== От математики к искусству ===
[[Файл:Les Demoiselles d'Avignon.jpg|thumb|upright|Протокубизм: при написании «[[Авиньонские девицы|Авиньонских девиц]]» (1907) [[Пабло Пикассо]] использовал проекцию [[Четвёртое измерение в изобразительном искусстве|четвёртого измерения]], чтобы показать и фас, и профиль одновременно<ref>{{cite book |last1=Cucker |first1=Felix |title=Manifold Mirrors: The Crossing Paths of the Arts and Mathematics |date=2013 |publisher=Cambridge University Press |isbn=978-0-521-72876-8 |pages=315–317}}</ref>]]

Известно, что книгу «Наука и гипотеза» (1902) математика и [[Теоретическая физика|физика]] [[Пуанкаре, Анри|Анри Пуанкаре]] читали многие [[Кубизм|кубисты]], в том числе [[Пабло Пикассо]] и [[Метценже, Жан|Жан Метценже]]<ref name="Miller"/><ref>{{cite book |author=Miller, Arthur I. |title=Insights of Genius: Imagery and Creativity in Science and Art |publisher=Springer |year=2012 |isbn=1-4612-2388-1}}</ref>. Пуанкаре видел в [[Евклидова геометрия|евклидовой геометрии]] не объективную истину, но всего лишь одну из многих возможных геометрических конфигураций. Возможное существование [[Четвёртое измерение в изобразительном искусстве|четвёртого измерения]]вдохновляло художников на вызов классической перспективе ренессанса, и они обратились к [[Неевклидова геометрия|неевклидовым геометриям]]<ref name=Henderson>{{cite book |author=Henderson, Linda D. |title=The Fourth Dimension and Non-Euclidean geometry in Modern Art |publisher=Princeton University Press |year=1983}}</ref><ref>{{cite book|url=http://eres.lndproxy.org/edoc/AH317Antliff-09.pdf |author1=Antliff, Mark |author2=Leighten, Patricia Dee |title=Cubism and Culture |publisher=Thames & Hudson |year=2001 }}{{dead link|date=June 2017 |bot=InternetArchiveBot |fix-attempted=yes }}</ref><ref>{{cite book |last=Everdell |first=William R. |authorlink=William Everdell |title=The First Moderns: Profiles in the Origins of Twentieth-Century Thought |year=1997 |publisher=University of Chicago Press |isbn=0-226-22480-5 |page=312}}</ref>. Одной из предпосылок кубизма стала идея о математическом — в цвете и форме — выражении сюжета. С кубизма начинается история [[абстракционизм]]а<ref>{{cite book |author=Green, Christopher |title=Cubism and its Enemies, Modern Movements and Reaction in French Art, 1916–1928 |publisher=Yale University Press |year=1987 |pages=13–47}}</ref>. В 1910 году Метценже писал: «[Пикассо] создаёт свободную, подвижную перспективу, из которой тот изобретательный математик Морис Принсе вывел целую геометрию»<ref>{{cite journal |last=Metzinger |first=Jean |authorlink=Jean Metzinger |date=October–November 1910 |title=Note sur la peinture |journal=Pan |page=60}} in {{cite book |last=Miller |title=Einstein, Picasso |publisher=Basic Books |page=167}}</ref>. В своих мемуарах Метценже вспоминал:

<blockquote>Морис Принсе часто навещал нас;... он осмыслял математику словно художник, словно эстет он взывал к ''n''-мерным континуумам. Ему нравилось прививать художникам интерес к [[Диаграмма Шлегеля|новым взглядам на пространство]], которые открыл [[Шлегель, Станислав Фердинанд Виктор|Шлегель]] и некоторые другие. В этом он преуспевал.»<ref>{{cite book |last=Metzinger |first=Jean |authorlink=Jean Metzinger |title=Le cubisme était né |year=1972 |publisher=Éditions Présence |pages=43–44}} in {{cite book |last=Ferry |first=Luc |authorlink=Luc Ferry |others=Robert De Loaiza, trans. |title=Homo Aestheticus: The Invention of Taste in the Democratic Age |year=1993 |publisher=University of Chicago Press |isbn=0-226-24459-8 |page=215}}</ref></blockquote>

Моделирование математических форм в исследовательских или преподавательских целях неизбежно ведёт к появлению причудливых или красивых фигур. Их влияние испытали [[Дадаизм|дадаисты]] [[Ман Рэй]]<ref>{{cite web |title=Man Ray–Human Equations A Journey from Mathematics to Shakespeare. February 7 – May 10, 2015 |url=http://www.phillipscollection.org/events/2015-02-07-exhibition-man-ray-human-equations |publisher=Phillips Collection|accessdate=5 September 2015}}</ref>, [[Дюшан, Марсель|Марсель Дюшан]]<ref>{{cite journal |last1=Adcock |first1=Craig |title=Duchamp's Eroticism: A Mathematical Analysis |journal=Iowa Research Online |date=1987 |volume=16 |issue=1 |pages=149–167 |url=http://ir.uiowa.edu/cgi/viewcontent.cgi?article=1208&context=dadasur}}</ref> и [[Эрнст, Макс|Макс Эрнст]]<ref name="Elder2013">{{cite book |last=Elder |first=R. Bruce |title=DADA, Surrealism, and the Cinematic Effect |url=https://books.google.com/books?id=mhXaAgAAQBAJ&pg=PA602 |year=2013 |publisher=Wilfrid Laurier University Press |isbn=978-1-55458-641-7 |page=602}}</ref><ref>{{cite book |author=Tubbs, Robert |title=Mathematics in Twentieth-Century Literature and Art: Content, Form, Meaning |url=https://books.google.com/books?id=h1vBAwAAQBAJ&pg=PA118 |year=2014 |publisher=JHU Press |page=118 |isbn=978-1-4214-1402-7}}</ref>, а также [[Сугимото, Хироси|Хироси Сугимото]]<ref>{{cite web|title=Hiroshi Sugimoto Conceptual Forms and Mathematical Models February 7 – May 10, 2015 |url=http://www.phillipscollection.org/events/2015-02-07-exhibition-hiroshi-sugimoto |publisher=Phillips Collection |accessdate=5 September 2015}}</ref>.

{{Заготовка раздела}}
{{Заготовка раздела}}


Версия от 20:14, 7 июня 2017

Математика в искусстве: резцовая гравюра на меди «Меланхолия» Альбрехта Дюрера, 1514 год. Видны следующие отсылки к математике: циркуль, магический квадрат и усечённый ромбоэдр. Также мы можем наблюдать весы и песочные часы[1]
Изучение вазы как тела вращения. Паоло Уччелло, XV век

Математика и искусство связаны друг с другом множеством способов. Математика сама по себе может считаться видом искусства, поскольку в ней обнаруживается своеобразная красота. Следы математического мышления проявляются в музыке, танце, живописи, архитектуре, скульптуре и тканном искусстве. Данная статья посвящена связи математики с изобразительным искусством.

Математика и искусство имеют длительную историю взаимоотношений. Художники прибегали к математическим концептам с IV века до н. э., когда греческий скульптор Поликлет Старший написал свой «Канон», где рекомендовал пропорцию 1:√2 для изображения нагого мужчины. Античные мыслители неотступно призывали художников и архитекторов применять в своей работе золотое сечение, однако никакого математического обоснования они не предлагали. Итальянский математик Лука Пачоли, важная фигура итальянского Возрождения, написал трактат «О божественной пропорции» (итал. De divina proportione), иллюстрированный ксилографиями Леонардо да Винчи. Другой итальянский художник Пьеро делла Франческа развил идеи Евклида о перспективе, написав трактат «О перспективе в живописи» (итал. De Prospectiva Pingendi). Гравёр Альбрехт Дюрер неоднократно делал математические ссылки в своей «Меланхолии». График XX века М. К. Эшер, консультируемый математиком Гарольдом Коксетером, широко применял образы паркета и гиперболической геометрии. Художники движения «Де Стейл» во главе с Тео ван Дусбургом и Питом Мондрианом явным образом использовали геометрические мотивы. Математика оказала влияние на различные формы вязания, вышивки, плетения и ковроделия. Для исламского искусства характерны симметрии, присутствующие в персидских и марокканских кладках, перфорированных каменных ширмах Великих Моголов, распространённых сотовых сводах.

Именно математика снабдила художников такими инструментами, как линейная перспектива, анализ симметрий и передала их всевозможные геометрические объекты, например, многогранники или ленту Мёбиуса. Преподавательская практика вдохновила Магнус Веннинджер на создание разноцветных звёздчатых многогранников. В картинах Рене Магритта и гравюрах Эшера используются рекурсии и логические парадоксы. Компьютерным формам искусства доступна фрактальная графика, в частности, визуалиазация множества Мандельброта. В некоторых работах иллюстрируются клеточные автоматы. Художник Дэвид Хокни высказал горячо оспариваемую гипотезу о применении его коллегами камеры-люциды ещё со времён Возрождения — она помогала точно изобразить место действия. Архитектор Филип Стедмэн утверждает, что Ян Вермеер задействовал камеру-обскуру.

Связь между математикой и искусством выражается и во многом другом. Предметы искусства подвергаются алгоритмическому анализу с помощью рентгенофлуоресцентной спектроскопии. Было установлено, что традиционный батик со всех уголков Явы имеют фрактальную размерность от 1 до 2. Наконец, искусство дало толчок некоторым математическим исследованиям. Филиппо Брунеллески сформулировал теорию перспективы, делая архитектурные чертежи, а позже Жерар Дезарг развил её, заложив основы проективной геометрии. Пифагорейская идея о Боге-геометре созвучна принципам сакральной геометрии, которая также нашла отражение в искусстве. Характерный пример — «Ветхий денми» Уильяма Блейка.

Истоки: от Древней Греции до Возрождения

Поликлетовы «Канон» и «симметрия»

Римская мраморная копия «Дорифора», оригинал выполнен Поликлетом в бронзе

Поликлет Старший (ок. 450—420 до н. э.) — греческий скульптор аргосской школы, современник Фидия. Его работы — в большинстве изображения атлетов — исполнялись преимущественно в бронзе. Согласно философу и математику Ксенократу, создатель «Дорифора» и статуи Геры в аргосском Герайоне считался одним из крупнейших скульпторов античности ].[2]. Хотя его произведения и уступали в известности скульптурам Фидия, они получили широкое признание среди ценителей. В своём трактате «Канон» Поликлет излагает математический подход к ваянию человеческого тела. По замыслу автора «Канон» должен был установить стандарт идеальных анатомических пропорций в изображении мужской наготы[2].

Все измерения человеческого тела он соотносит с дистальной фалангой мизинца[3]. Чтобы рассчитать длину средних фаланг Поликлет умножает длину дистальной на квадратный корень из двух (√2). Проделав эту операцию ещё раз, он определяет идеальную длину проксимальной фаланги. Затем он умножает длину пальца на √2 и получает длину ладони от основания пальца до локтевой кости. Данный геометрический ряд продолжается, и Поликлет рассчитывает измерения руки, груди, туловища и т. д.[4]

Влияние «Канона» распространилось на скульптуру Древней Грации, Древнего Рима и Возрождения. Ни одна из работ Поликлета не дошла до наших дней, однако существуют математически точные римские копии. Некоторые исследователи утверждают, что Поликлет в свою очередь испытал влияние пифагорейства[5]. «Канон» оперирует основными концепциями древнегреческой геометрии: отношением, пропорцией и симметрией. Система «Канона» позволяет описать человеческую фигуру посредством непрерывных геометрических прогрессий[3].

Перспектива и пропорция

Эксперимент Брунеллески с линейной перспективой

В античный период художники не прибегали к линейной перспективе. Размер объектов был обусловлен не их отдалённостью, но тематической важностью. Некоторые художники Средневековья использовали обратную перспективу для привлечения внимания к особо значимым фигурам. В 1021 году исламский математик Ибн аль-Хайсам сформулировал теорию оптики, однако к предметам искусства её не применял[6]. Эпоха Возрождения связана с реставрацией древнегреческой и древнеримской культурных традиций. Возродилась и идеи о применении математики для изучения природы и искусства. Художники позднего Средневековья и Ренессанса интересовались математикой по двум причинам. Во-первых, живописцы желали знать, как верно изображать трёхмерные объекта на двумерной поверхности холста. Во-вторых, деятели искусств, как и некоторые философы, верили в математику как истинную суть физического мира; изобразительное искусство как часть этой Вселенной подчинено законам геометрии[7].

Зачатки перспективы наблюдаются у Джотто (1266 – 1337), который писал отдалённые объекты, алгебраически определяя положение линий в перспективе. В 1415 году архитектор Филиппо Брунеллески вместе с другом Леоном Баттистой Альберти представили во Флоренции геометрический метод создания перспективы. Применяя подобные треугольники Евклида, они высчитывали видимую высоту отдалённых объектов[8][9]. Картины с перспективой самого Брунеллески утрачены, однако «Троица» Мазаччо позволяет увидеть принцип в действии[6][10][11].

Паоло Уччелло новаторски использовал перспективу в своей «Битве при Сан-Романо» (ок. 1435–1460)

Итальянский живописец Паоло Уччелло (1397–1475) был потрясён новой техникой. В «Битве при Сан-Романо» он разместил сломанные копья между линиями перспективы[12][13].

Творчество Пьеро делла Франческа (ок. 1415–1492) служит примером перехода итальянского Ренессанса к новой идеологии. Будучи крупным математиком и, в частности, геометром, он писал труды по стереометрии и теории перспективы. В их числе «О перспективе в живописи» (итал. De Prospectiva Pingendi), «Трактат о счётах» (итал. Trattato d'Abaco) и «О правильных многогранниках» (итал. De corporibus regularibus)[14][15][16]. Историк Джорджо Вазари в «Жизнеописаниях» называет Пьеро «величайшим геометром своего времени, а, может, и всех времён»[17]. Интерес Пьеро к перспективе виден в его работах «Полиптих святого Антония»[18], «Алтарь святого Августина» и «Бичевание Иисуса Христа». Его геометрические изыскания повлияли на следующие поколения математиков и художников, среди которых были Лука Пачоли и Леонардо да Винчи. Известно, что Пьеро изучал работы древних математиков, в том числе Архимеда[19]. Пьеро обучался коммерческой арифметике в «школе абака»; его трактаты оформлены в том же стиле, что и учебники «школы»[20]. Возможно, Пьеро был знаком с «Книгой Абака» (1202) Фибоначчи. Линейная перспектива постепенно проникала в мир искусства. В трактате «О живописи» (итал. De pictura, 1435) Альберти писал: «лучи света идут от точек на картине к глазу вдоль прямой линии, формируя пирамиду, где глаз есть вершина». Картина, написанная по принципу линейной перспективы есть разрез этой пирамиды[21].

В труде «О перспективе в живописи» Пьеро преобразует свои эмпирические наблюдения о перспективе в математические выражения и доказательства. Следуя Евклиду, он определяет точку как «мельчайший уловимый глазу объект» (итал. una cosa tanto picholina quanto e possible ad ochio comprendere)[7].Пьеро подводит читателя к представлению трёхмерных тел на двумерной поверхности с помощью дедуктивных умозаключений[22].

Современный художник Дэвид Хокни утверждает, что с 1420-х годов его коллеги применяли камеру-люциду, что привело к резкому повышению точности и реалистичности картин. Он считает, что этим приспособлением пользовались и Энгр, и ван Эйк, и Караваджо[23]. Мнение экспертов по этому вопросу расходится[24][25]. Архитектор Филип Стедмэн озвучил ещё одну спорную гипотезу[26] об использовании Вермеером камеры-обскуры[27].

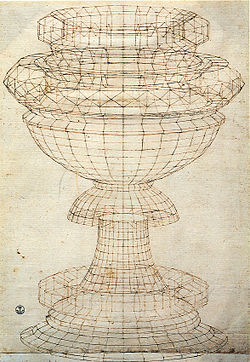
В 1509 году Лука (ок. 1447–1517) опубликовал трактат «О божественной пропорции», посвящённый математическому и художественному аспектам пропорции, в том числе и человеческого лица. Леонардо да Винчи (1452–1519), учившийся у Пачоли в 1490-х годах, иллюстрировал его текст ксилографиями правильных многогранников. Каркасные изображения многогранников, сделанные да Винчи, – первые дошедшие до нас иллюстрации такого характера[28]. Одним из первых он изобразил многогранники (в их числе ромбокубооктаэдр), построенные на гранях других фигур – так Леонардо демонстрировал перспективу. Сам трактат посвящён описанию перспективы в работах Пьеро делла Франческа, Мелоццо да Форли и Марко Пальмеццано[29]. Да Винчи изучил «Сумму» Пачоли, скопировав оттуда таблицы с пропорциями[30]. И «Джоконда», и «Тайная вечеря» выстроены по принципу линейной перспективы с исчезающей точкой, которая придаёт картине видимую глубину[31]. «Тайная вечеря» использует пропорции 12:6:4:3 – они же присутствуют в «Афинской школе» Рафаэля. Изображённый на ней Пифагор держит таблицу идеальных пропорций, которым пифагорейцы придавали сакральный смысл[32][33]. Витрувианский человек Леонардо отражает идеи римского архитектора Витрувия; две наложенные мужские фигуры вписаны и в круг, и в квадрат[34].

Уже в XV веке живописцы, интересовавшиеся визуальными искажениями, применяли криволинейную перспективу. На «Портрете четы Арнольфини» (1343) Яна ван Эйка есть выпуклое зеркало, отражающее фигуры героев[35]. «Автопортрет в выпуклом зеркале» (ок. 1523–1524) Пармиджанино изображает практически неискажённое лицо художника и сильно изогнутые задний план и руку, расположенную на краю[36].

Трёхмерные объекты можно вполне убедительно изобразить, не прибегая к перспективе. Наклонные проекции, в том числе кавалерская перспектива (использовалась французскими баталистами в XVIII веке для написания фортификаций), непрерывно и повсеместно наблюдается у китайских художников с I-II по XVIII века. К китайцам эта традиция пришла из Индии, туда же – из Древнего Рима. Наклонная проекция наблюдается в японском искусстве, например, на картинах Тории Киёнаги в стиле укиё-э[37].

Золотое сечвние

Золотое сечение, приблизительно равное 1,618, было известно ещё Евклиду[38]. Многие современники утверждают[39][40][41][42], что оно применялось в искусстве и архитектуре Древнего Египта, Древней Греции, однако достоверных подтверждений этому нет[43]. Возникновение этого предположения может быть вызвано путаницей между золотым сечением и «золотой серединой», которой греки называли «отсутствие излишка во всяком из направлений»[43]. Пирамидологи с XIX века говорят о применении золотого сечения при проектировании пирамид, аргументируя позицию сомнительными математическими доводами[43][44][45]. Скорее всего пирамиды были построены либо на основе треугольника со сторонами 3–4–5 (угол наклона — 53°8'), который упомянут в папирусе Ахмеса, либо на основе треугольника с косинусом π/4 (угол наклона — 51°50')[46]. Фасад и пол Парфенона, построенного в V веке до н.э. в Афинах, якобы спроектированы на основе золотого сечения[47][48][49]. Это утверждение также опровергается реальными измерениями[43]. Считается, что золотое сечение применялось и при проектировании Великой мечети Кайруана в Тунисе[50]. Тем не менее, данная величина не обнаруживается в оригинальном проекте мечети[51]. В Историк архитектуры Фредерик Макоди Лунд в 1919 году заявлял, что Шартрский собор (XII век), ланский (1157–1205) и парижский собор Нотр-Дам (1160) спроектированы в соответствии с принципом золотого сечения[52]. Некоторые исследователи утверждают, что до выхода труда Пачоли в 1509 году сечение не было известно ни художникам, ни архитекторам[53]. Например, высота и ширина фасада ланского собора Нотр-Дам имеют отношение 8/5 или 1.6, но не 1,618. Подобная пропорция является одним из отношений Фибоначчи, которые трудно отличить от золотого сечения, поскольку они сходятся к 1,618[54]. Золотое сечение наблюдается у последователей Пачоли, в том числе в «Джоконде» Леонардо[55].

Плоскостные симметрии

Плоскостные симметрии на протяжении нескольких тысяч лет наблюдаются в ковроткачестве, мощении, тканном искусстве и создании решётчатых объектов[56][57][58][59].

Многие традиционные ковры, будь то ворсистые или килимы (плоскотканые), включают центральную часть и её обрамление. Оба объекта могут содержать симметричные элементы, при этом на коврах ручной работы симметрия часто нарушается авторскими деталями, вариацией узора и цвета[56]. Анатолийские килимы часто используют мотивы, сами по себе обладающие симметрией. Стандартный план ковра часто подразумевает наличие полос, в том числе с перемежающимися мотивами, а также подобий шестиугольных форм.

Искусные индийские решётки джали, создаваемые из мрамора, украшают дворцы и гробницы[57]. Китайские решётки, всегда наделённые некой симметрией, — часто зеркальной, двойной зеркальной или вращательной — представлены в 14 из 17 групп обоев. Некоторые обладают центральным медальоном, некоторые — краем, принадлежащем группе бордюров[60]. Многие китайские решётки были математически проанализированы Дэниелом С. Даем. Ему удалось установить, что центром данного искусства является провинция Сычуань[61].

Персидская мозаика гирих

Симметрии распространены в таких тканных искусствах, как стёжка[58], вязание[62], вязание крючком[63], вышивка[64][65], вышивка крестом и ткачество[66]. Примечательно, что симметрия на ткани может быть чисто декоративной или символизировать статус обладателя[67]. Вращательная симметрия имеет место в циркулярных объектах. Многие купола украшены симметричными узорами внутри и снаружи как, например, мечеть Шейха Лютфуллы (1619) в Исфахане[68]. Рефлексивные и вращательные симметрии характерны для вышитых и кружевных элементов скатертей и настольных ковриков, созданных при помощи катушек или техникой фриволите. Эти объекты также подвергаются математическому изучению[69].

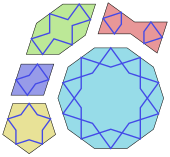
Исламское искусство демонстрирует симметрии во многих формах, в особенности это свойственно персидской мозаике гирих. Она создаётся пятью плиточными формами: правильным десятиугольником, правильным пятиугольником, вытянутым десятиугольником, ромбом и фигурой, напоминающей галстук-бабочку. Все стороны этих фигур равны, все их углы кратны 36° (π/5 радиан), что даёт пяти- и десятикратные симметрии. Плитка украшена переплетающимся орнаментом (собственно гирих), который обычно более заметен, чем края плитки. В 2007 году физики Питер Лу и Пол Стейнхардт отметили сходство гирих с квазикристаллическими плитками Пенроуза[70]. Геометрически выверенная плитка зулляйдж является характерным элеменом марокканской архитектуры[59]. Сотовые саоды или мукарнасы трёхмерны, однако проектировались они — путём рисования геометрических ячеек — в двух измерениях[71].

Многогранники

Первая печатная иллюстрация ромбокубооктаэдра. Леонардо да Винчи, «О божественной пропорции», 1509

Правильные многогранники — один из распространённых сюжетов западного искусства. Малый звёздчатый додекаэдр, например, встречается в мраморной мозаике Собора Святого Марка в Венеции; авторство приписывают Паоло Уччелло[12]. Правильные многогранники да Винчи иллюстрируют труд «О божественной пропорции» Луки Пачоли[12]. Стеклянный ромбокубооктаэдр встречается на портрете Пачоли (1495), написанном Якопо де Барбари[12]. Усечённый многогранник и многие другие связанные с математикой объекты присутствуют на гравюре Дюрера «Меланхолия»[12]. «Тайная вечеря» Сальвадора Дали изображает Христа и его учеников внутри гигантского додекаэдра.

Альбрехт Дюрер (1471–1528), гравёр и график немецкого Ренессанса, внёс свой вклад в теорию, выпустив в 1525 году книгу «Руководство к измерению» (нем. Underweysung der Messung). Труд посвящён линейной перспективе, геометрии в архитектуре, правильным многогранникам и многоугольникам. Вероятно, Дюрер вдохновился работами Пачоли и Пьеро делла Франческа во время путешествий по Италии[72]. Образцы перспективы в «Руководстве к измерению» не до конца проработаны и неточны, однако многогранники Дюрер осветил в полной мере. Именно в этом тексте впервые упомянута развёртка многогранника, то есть разворачивание (например, бумажного) многогранника в плоскую фигуру, которую можно напечатать[73]. Ещё одна влиятельный труд Дюрера — «Четырёх книг о человеческих пропорциях» (нем. Vier Bücher von Menschlicher Proportion, 1528)[74].

Известная гравюра Дюрера «Меланхолия» изображает опечаленного мыслителя, сидящего у усечённого треугольного трапецоэдра и магического квадрата[1]. Два этих объекта и гравюра в целом представляют для современных исследователей наибольший во всём творчестве Дюрера интерес[1][75][76]. Петер-Клаус Шустер выпустил о «Меланхолии» двухтомную книгу[77], в то время как Эрвин Панофский дискутирует о произведении в своей монографии[1][78]. «Гиперкубическое тело» Сальвадора Дали содержит трёхмерную развёртку гиперкуба — четырёхмерного правильного многогранника[79].

Фрактальные размерности

Яванский батик из Суракарты, узор паранг клитик. Подобные узоры имеют фрактальную размерность от 1.2 до 1.5

Традиционная индонезийская роспись на ткани батик использует в качестве резерва воск. Её мотивы могут соответствовать элементам окружающего мира (например, растениям) или же быть абстрактными, даже хаотическими. Резерв может наноситься неточно, крекинг (растрескивание) воска усиливает эффект случайности. Роспись имеет фрактальную размерность от 1 до 2, в зависимости от региона происхождения. Например, батик из Чиребона имеет размерность 1,1, размерность батика из Джокьякарты и Суракарты (центральная Ява) — от 1,2 до 1,5; ласемский (северная Ява) и тасикмалайский (западная Ява) обладают размерностью от 1,5 до 1,7[80].

Работы современного художника Джексона Поллока в капельной технике дриппинг также примечательны своей фрактальной размерностью: Картина «Номер 14» (англ. Number 14, 1948) имеет размерность 1,45. Его последующие работы характеризуются более высокой размерностью, что свидетельствует о лучшей проработке закономерностей. Одна из последних картин Поллока «Синие столбы» (англ. Blue Poles) имеет размерность 1,72, а её написание заняло шесть месяцев[81].

Сложные взаимосвязи

Астроном Галилео Галилей в трактате «Пробирных дел мастер» писал, что вселенная написана на языке математики, и что символы этого языка есть треугольники, круги и иные геометрические фигуры[82]. По мнению Галилея, жаждущие познать природу художники должны в первую очередь понимать математику. Математики же пытались анализировать изобразительной искусство через призму геометрии и рациональности (в математическом смысле слова). Математик Фелипе Кукер предположил, что эта наука и в особенности геометрия служат сводом правил для «закономерного художественного созидания» (англ. "rule-driven artistic creation"), хотя и не единственным[83]. Некоторые особо примечательные образцы этой сложной взаимосвязи описаны ниже[84].

Математик Г. Х. Харди определил набор критериев, соответствие которым свидетельствует о математической красоте

Математика как искусство

Математик Джерри П. Кинг пишет о математике как о искусстве, утверждая, что ключами к ней являются красота и элегантность, а вовсе не скучный формализм. Кинг считает, что именно красота мотивирует исследователей в этой области[85]. Он цитирует эссе «Апология математика» (1940) другого математика Г. Х. Харди, где тот признаётся в любви к двум античным теоремам: доказательству бесконечности простых чисел Евклида и доказательству иррациональности квадратного корня из двух. Последнюю Кинг оценивает по выработанным Харди критериям красоты в математике: серьёзности, глубине, общности, неожиданности, неизбежности и экономии (курсив Кинга) и заключает, что доказательство «эстетически привлекательно»[86]. Венгерский математик Пал Эрдёш также говорит о красоте математики, не всякое измерение которой можно выразить словами: «Почему числа красивы? Равнозначно было бы спросить, почему красива Девятая симфония Бетховена. Если вы этого не видите, никто не сможет вам объяснить. Я ‘’знаю’’, что числа красивы.» [87][88]

Математический инструментарий искусства

Следы математики различимы во многих видах искусства: музыке, танце[89], живописи, архитектуре, скульптуре. Получаемые взаимосвязи весьма разнообразны[90]. В контексте изобразительных искусств математика даёт творцу множество инструментов наподобие линейной перспективы, описанной Бруком Тейлором и Иоганном Ламбертом, или начертательной геометрии, наблюдаемой ещё у Альбрехта Дюрера и Гаспара Монжа, а ныне применяемой для программного моделирования трёхмерных объектов[91]. Начиная со Средневековья (Пачоли) и Возрождения (да Винчи и Дюрер) художники применяли достижения математики в творческих целях[90][92]. За вычетом зачатков перспективы в древнегреческой архитектуре её широкое использование началось в XIII веке, среди пионеров был Джотто. Правило исчезающей точки сформулировал Брунеллески в 1413 году[6]. Его открытие вдохновило не только да Винчи и Дюрера, но и Исаака Ньютона, исследовавшего оптический спектр, Гёте, написавшего книгу «К теории цвета», а затем и новые поколения художников, среди которых были Филипп Отто Рунге, Уильям Тёрнер[93], прерафаэлиты и Василий Кандинский[94][95]. Также художники исследуют симметрии, присутствующие в композиции[96]. Математический инструментарий может применяться учёными, изучающими предметы искусства, или самими мастерами как в случае графика М. К. Эшера (при участии Гарольда Коксетера) или архитектора Фрэнка Гери. Последний утверждает, что системы автоматизированного проектирования дали ему совершенно новые пути самовыражения[97].

Художник Ричард Райт считает, что визуальные модели математических объектов служат либо для симуляции некого явления, либо являются предметами компьютерного искусства. Райт иллюстрирует свою позицию изображением множества Мандельброта, созданным клеточным автоматом и компьютерным рендером; ссылаясь на тест Тьюринга, он рассуждает, могут ли продукты алгоритмов считаться искусством[98]. Тот же подход наблюдается и у Сашо Калайдзевского, который рассматривает визуализируемые математические объекты: паркет, фракталы, фигуры гиперболической геометрии[99].

Одним из пионеров компьютерного искусства был Десмонд Пол Генри, создавший «Рисовальную машину 1». Аналоговый вычислительный механизм на базе компьютера бомбового прицела был представлен публике в 1962 году[100][101]. Машина могла создавать сложные, абстрактные, асимметричные, криволинейные, но повторяющиеся рисунки[100][102]. Хамид Надери Йеганех создаёт фигуры рыб, птиц и иных объектов реального мира, используя семейства кривых[103][104][105]. Современные художники, в том числе Микаэль Х. Кристенсен, работают в жанре алгоритмического искусства, создавая сценарии для программного обеспечения. Ведомая художником система применяет математические операции к заданному массиву данных[106][107].

  • Математическая скульптура Батшебы Гроссмана, 2007
    Математическая скульптура Батшебы Гроссмана, 2007
  • Фрактальная скульптура: 3D Fraktal 03/H/dd Хартмута Скербиша, 2003
    Фрактальная скульптура: 3D Fraktal 03/H/dd Хартмута Скербиша, 2003
  • Слово Фибоначчи: деталь произведения Самюэля Моннье, 2009
    Слово Фибоначчи: деталь произведения Самюэля Моннье, 2009
  • Предмет компьютерного искусства, созданный «Рисовальной машиной 1» Десмонда П. Генри, 1962
    Предмет компьютерного искусства, созданный «Рисовальной машиной 1» Десмонда П. Генри, 1962
  • «Летящая птица» Хамида Надери Йеганеха образована семейством кривых
    «Летящая птица» Хамида Надери Йеганеха образована семейством кривых

От математики к искусству

Файл:Les Demoiselles d'Avignon.jpg
Протокубизм: при написании «Авиньонских девиц» (1907) Пабло Пикассо использовал проекцию четвёртого измерения, чтобы показать и фас, и профиль одновременно[108]

Известно, что книгу «Наука и гипотеза» (1902) математика и физика Анри Пуанкаре читали многие кубисты, в том числе Пабло Пикассо и Жан Метценже[109][110]. Пуанкаре видел в евклидовой геометрии не объективную истину, но всего лишь одну из многих возможных геометрических конфигураций. Возможное существование четвёртого измерениявдохновляло художников на вызов классической перспективе ренессанса, и они обратились к неевклидовым геометриям[111][112][113]. Одной из предпосылок кубизма стала идея о математическом — в цвете и форме — выражении сюжета. С кубизма начинается история абстракционизма[114]. В 1910 году Метценже писал: «[Пикассо] создаёт свободную, подвижную перспективу, из которой тот изобретательный математик Морис Принсе вывел целую геометрию»[115]. В своих мемуарах Метценже вспоминал:

Морис Принсе часто навещал нас;... он осмыслял математику словно художник, словно эстет он взывал к n-мерным континуумам. Ему нравилось прививать художникам интерес к новым взглядам на пространство, которые открыл Шлегель и некоторые другие. В этом он преуспевал.»[116]

Моделирование математических форм в исследовательских или преподавательских целях неизбежно ведёт к появлению причудливых или красивых фигур. Их влияние испытали дадаисты Ман Рэй[117], Марсель Дюшан[118] и Макс Эрнст[119][120], а также Хироси Сугимото[121].

Примечания

  1. ↑ 1 2 3 4 Ziegler, Günter M. Dürer's polyhedron: 5 theories that explain Melencolia's crazy cube. The Guardian (3 декабря 2014). Дата обращения: 27 октября 2015.
  2. ↑ 1 2 Stewart, Andrew (November 1978). "Polykleitos of Argos," One Hundred Greek Sculptors: Their Careers and Extant Works". Journal of Hellenic Studies. 98: 122—131. doi:10.2307/630196. JSTOR 630196.
  3. ↑ 1 2 Tobin, Richard (October 1975). "The Canon of Polykleitos". American Journal of Archaeology. 79 (4): 307—321. doi:10.2307/503064.
  4. ↑ Lawton, Arthur J. (2013). "Pattern, Tradition and Innovation in Vernacular Architecture". Past. 36. Дата обращения: 25 июня 2015. The base figure is a square the length and width of the distal phalange of the little finger. Its diagonals rotated to one side transform the square to a 1 : √2 root rectangle. In Figure 5 this rectangular figure marks the width and length of the adjacent medial phalange. Rotating the medial diagonal proportions the proximal phalange and similarly from there to the wrist, from wrist to elbow and from elbow to shoulder top. Each new step advances the diagonal's pivot point.
  5. ↑ Raven, J. E. (1951). "Polyclitus and Pythagoreanism". Classical Quarterly. 1 (3—4): 147–. doi:10.1017/s0009838800004122.
  6. ↑ 1 2 3 O'Connor, J. J.; Robertson, E. F. Mathematics and art – perspective. University of St Andrews (январь 2003). Дата обращения: 1 сентября 2015.
  7. ↑ 1 2 The Visual Mind II / Emmer, Michelle. — MIT Press, 2005. — ISBN 978-0-262-05048-7.
  8. ↑ Vasari, Giorgio. Lives of the Artists. — Torrentino, 1550. — P. Chapter on Brunelleschi.
  9. ↑ Alberti, Leon Battista. On Painting / Leon Battista Alberti, John R. Spencer. — Yale University Press, 1956.
  10. ↑ Field, J. V. The Invention of Infinity: Mathematics and Art in the Renaissance. — Oxford University Press, 1997. — ISBN 978-0-19-852394-9.
  11. ↑ Witcombe, Christopher L. C. E. Art History Resources. Дата обращения: 5 сентября 2015.
  12. ↑ 1 2 3 4 5 Hart, George W. Polyhedra in Art. Дата обращения: 24 июня 2015.
  13. ↑ Cunningham, Lawrence. Culture and Values: A Survey of the Western Humanities / Lawrence Cunningham, John Reich, Lois Fichner-Rathus. — Cengage Learning, 1 January 2014. — P. 375. — «which illustrate Uccello's fascination with perspective. The jousting combatants engage on a battlefield littered with broken lances that have fallen in a near-grid pattern and are aimed toward a vanishing point somewhere in the distance.». — ISBN 978-1-285-44932-6.
  14. ↑ della Francesca, Piero. De Prospectiva Pingendi / G. Nicco Fasola. — Florence, 1942.
  15. ↑ della Francesca, Piero. Trattato d'Abaco / G. Arrighi. — Pisa, 1970.
  16. ↑ della Francesca, Piero. L'opera "De corporibus regularibus" di Pietro Franceschi detto della Francesca usurpata da Fra Luca Pacioli / G. Mancini. — 1916.
  17. ↑ Vasari, G. Le Opere, volume 2 / G. Milanesi. — 1878. — P. 490.
  18. ↑ Zuffi, Stefano. Piero della Francesca. — L'Unità – Mondadori Arte, 1991. — P. 53.
  19. ↑ Heath, T.L. The Thirteen Books of Euclid's Elements. — Cambridge University Press, 1908. — P. 97.
  20. ↑ Grendler, P. What Piero Learned in School: Fifteenth-Century Vernacular Education / M.A. Lavin. — University Press of New England, 1995. — P. 161–176.
  21. ↑ Alberti, Leon Battista. On Painting / Alberti, Leon Battista, Grayson, Cecil (trans.). — Penguin Classics, 1991.
  22. ↑ Peterson, Mark. The Geometry of Piero della Francesca. — «In Book I, after some elementary constructions to introduce the idea of the apparent size of an object being actually its angle subtended at the eye, and referring to Euclid's Elements Books I and VI, and Euclid's Optics, he turns, in Proposition 13, to the representation of a square lying flat on the ground in front of the viewer. What should the artist actually draw? After this, objects are constructed in the square (tilings, for example, to represent a tiled floor), and corresponding objects are constructed in perspective; in Book II prisms are erected over these planar objects, to represent houses, columns, etc.; but the basis of the method is the original square, from which everything else follows.»
  23. ↑ Hockney, David. Secret Knowledge: Rediscovering the Lost Techniques of the Old Masters. — Thames and Hudson, 2006. — ISBN 978-0-500-28638-8.
  24. ↑ Van Riper, Frank Hockney's 'Lucid' Bomb At the Art Establishment. The Washington Post. Дата обращения: 4 сентября 2015.
  25. ↑ Marr, Andrew What the eye didn't see. The Guardian (7 октября 2001). Дата обращения: 4 сентября 2015.
  26. ↑ Janson, Jonathan An Interview with Philip Steadman. Essential Vermeer (25 апреля 2003). Дата обращения: 5 сентября 2015.
  27. ↑ Steadman, Philip. Vermeer's Camera: Uncovering the Truth Behind the Masterpieces. — Oxford, 2002. — ISBN 978-0-19-280302-3.
  28. ↑ Hart, George. Luca Pacioli's Polyhedra. Дата обращения: 13 августа 2009.
  29. ↑ Morris, Roderick Conway Palmezzano's Renaissance:From shadows, painter emerges. New York Times (27 января 2006). Дата обращения: 22 июля 2015.
  30. ↑ Calter, Paul. Geometry and Art Unit 1. Dartmouth College. Дата обращения: 13 августа 2009.
  31. ↑ Brizio, Anna Maria. Leonardo the Artist. — McGraw-Hill, 1980.
  32. ↑ Ladwein, Michael. Leonardo Da Vinci, the Last Supper: A Cosmic Drama and an Act of Redemption. — Temple Lodge Publishing, 2006. — P. 61–62. — ISBN 978-1-902636-75-7.
  33. ↑ Turner, Richard A. Inventing Leonardo. — Alfred A. Knopf, 1992.
  34. ↑ Wolchover, Natalie Did Leonardo da Vinci copy his famous 'Vitruvian Man'? NBC News (31 января 2012). Дата обращения: 27 октября 2015.
  35. ↑ Criminisi, A.; Kempz, M.; Kang, S. B. (2004). "Reflections of Reality in Jan van Eyck and Robert Campin" (PDF). Historical Methods. 37 (3): 109—121. doi:10.3200/hmts.37.3.109-122.
  36. ↑ Cucker, Felix. Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. — Cambridge University Press, 2013. — P. 299–300, 306–307. — ISBN 978-0-521-72876-8.
  37. ↑ Cucker, Felix. Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. — Cambridge University Press, 2013. — P. 269–278. — ISBN 978-0-521-72876-8.
  38. ↑ Joyce, David E. Euclid's Elements, Book II, Proposition 11. Clark University (1996). Дата обращения: 24 сентября 2015.
  39. ↑ Seghers, M. J.; Longacre, J. J.; Destefano, G. A. (1964). "The Golden Proportion and Beauty". Plastic and Reconstructive Surgery. 34 (4): 382—386. doi:10.1097/00006534-196410000-00007.
  40. ↑ Mainzer, Klaus. Symmetries of Nature: A Handbook for Philosophy of Nature and Science. — Walter de Gruyter, 1996. — P. 118.
  41. ↑ Mathematical properties in ancient theatres and amphitheatres. Дата обращения: 29 января 2014.
  42. ↑ Architecture: Ellipse? The-Colosseum.net. Дата обращения: 29 января 2014.
  43. ↑ 1 2 3 4 Markowsky, George (January 1992). "Misconceptions about the Golden Ratio" (PDF). The College Mathematics Journal. 23 (1): 2—19. doi:10.2307/2686193.
  44. ↑ Taseos, Socrates G. Back in Time 3104 B.C. to the Great Pyramid. — SOC Publishers, 1990.
  45. ↑ Отношение наклонной высоты к половине длины основания составляет 1,619, что менее чем на 1% отличается от золотого сечения (1,618). Подразумевается использование треугольника Кеплера (угол наклона — 51°49').
  46. ↑ Gazale, Midhat. Gnomon: From Pharaohs to Fractals. — Princeton University Press, 1999. — ISBN 978-0-691-00514-0.
  47. ↑ Huntley, H.E. The Divine Proportion. — Dover, 1970.
  48. ↑ Hemenway, Priya. Divine Proportion: Phi In Art, Nature, and Science. — Sterling, 2005. — P. 96.
  49. ↑ Usvat, Liliana Mathematics of the Parthenon. Mathematics Magazine. Дата обращения: 24 июня 2015.
  50. ↑ Boussora, Kenza; Mazouz, Said (Spring 2004). "The Use of the Golden Section in the Great Mosque of Kairouan". Nexus Network Journal. 6 (1): 7—16. doi:10.1007/s00004-004-0002-y. The geometric technique of construction of the golden section seems to have determined the major decisions of the spatial organisation. The golden section appears repeatedly in some part of the building measurements. It is found in the overall proportion of the plan and in the dimensioning of the prayer space, the court and the minaret. The existence of the golden section in some parts of Kairouan mosque indicates that the elements designed and generated with this principle may have been realised at the same period.
  51. ↑ Brinkworth, Peter; Scott, Paul (2001). "The Place of Mathematics". Australian Mathematics Teacher. 57 (3): 2.
  52. ↑ Chanfón Olmos, Carlos. Curso sobre Proporción. Procedimientos reguladors en construcción. — Convenio de intercambio Unam–Uady. México – Mérica, 1991.
  53. ↑ Livio, Mario. The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. — Broadway Books, 2002.
  54. ↑ Smith, Norman A. F. (2001). "Cathedral Studies: Engineering or History" (PDF). Transactions of the Newcomen Society. 73: 95—137. doi:10.1179/tns.2001.005.
  55. ↑ McVeigh, Karen Why golden ratio pleases the eye: US academic says he knows art secret. The Guardian (28 декабря 2009). Дата обращения: 27 октября 2015.
  56. ↑ 1 2 Cucker, Felix. Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. — Cambridge University Press, 2013. — P. 89–102. — ISBN 978-0-521-72876-8.
  57. ↑ 1 2 Lerner, Martin. The flame and the lotus : Indian and Southeast Asian art from the Kronos collections. — Exhibition Catalogue. — Metropolitan Museum of Art, 1984.
  58. ↑ 1 2 Ellison, Elaine. Mathematical Quilts: No Sewing Required / Elaine Ellison, Diana Venters. — Key Curriculum, 1999.
  59. ↑ 1 2 Castera, Jean Marc. Arabesques. Decorative Art in Morocco / Jean Marc Castera, Francoise Peuriot. — Art Creation Realisation, 1999. — ISBN 978-2-86770-124-5.
  60. ↑ Cucker, Felix. Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. — Cambridge University Press, 2013. — P. 103–106. — ISBN 978-0-521-72876-8.
  61. ↑ Dye, Daniel S. Chinese Lattice Designs. — Dover, 1974. — P. 30–39.
  62. ↑ belcastro, sarah-marie (2013). "Adventures in Mathematical Knitting". American Scientist. 101 (2): 124. doi:10.1511/2013.101.124.
  63. ↑ Taimina, Daina. Crocheting Adventures with Hyperbolic Planes. — A K Peters, 2009. — ISBN 1-56881-452-6.
  64. ↑ Snook, Barbara. Florentine Embroidery. Scribner, Second edition 1967.
  65. ↑ Williams, Elsa S. Bargello: Florentine Canvas Work. Van Nostrand Reinhold, 1967.
  66. ↑ Grünbaum, Branko; Shephard, Geoffrey C. (May 1980). "Satins and Twills: An Introduction to the Geometry of Fabrics". Mathematics Magazine. 53 (3): 139—161. doi:10.2307/2690105. JSTOR 2690105.
  67. ↑ 1 2 Gamwell, Lynn. Mathematics and Art: A Cultural History. — Princeton University Press, 2015. — P. 423. — ISBN 978-0-691-16528-8.
  68. ↑ Baker, Patricia L. Iran / Patricia L. Baker, Hilary Smith. — 3. — Bradt Travel Guides, 2009. — P. 107. — ISBN 1-84162-289-3.
  69. ↑ Irvine, Veronika; Ruskey, Frank (2014). "Developing a Mathematical Model for Bobbin Lace". Journal of Mathematics and the Arts. 8 (3—4): 95—110. arXiv:1406.1532. doi:10.1080/17513472.2014.982938.
  70. ↑ Lu, Peter J.; Steinhardt, Paul J. (2007). "Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture". Science. 315 (5815): 1106—1110. Bibcode:2007Sci...315.1106L. doi:10.1126/science.1135491. PMID 17322056.
  71. ↑ van den Hoeven, Saskia, van der Veen, Maartje. Muqarnas-Mathematics in Islamic Arts. Дата обращения: 15 января 2016. Архивировано 27 сентября 2013 года.
  72. ↑ Panofsky, E. The Life and Art of Albrecht Durer. — Princeton, 1955.
  73. ↑ Hart, George W. Dürer's Polyhedra. Дата обращения: 13 августа 2009.
  74. ↑ Dürer, Albrecht. Hierinn sind begriffen vier Bucher von menschlicher Proportion. — Nurenberg : Archive.org, 1528.
  75. ↑ Schreiber, P. (1999). "A New Hypothesis on Durer's Enigmatic Polyhedron in His Copper Engraving 'Melencolia I'". Historia Mathematica. 26: 369—377. doi:10.1006/hmat.1999.2245.
  76. ↑ Dodgson, Campbell. Albrecht Dürer. — London : Medici Society, 1926. — P. 94.
  77. ↑ Schuster, Peter-Klaus. Melencolia I: Dürers Denkbild. — Berlin : Gebr. Mann Verlag, 1991. — P. 17–83.
  78. ↑ Panofsky, Erwin. Saturn and melancholy / Erwin Panofsky, Raymond Klibansky, Fritz Saxl. — Basic Books, 1964.
  79. ↑ Ошибка в сносках?: Неверный тег <ref>; для сносок CorpusHypercubus не указан текст
  80. ↑ Lukman, Muhamad; Hariadi, Yun; Destiarmand, Achmad Haldani (2007). "Batik Fractal : Traditional Art to Modern Complexity" (PDF). Proceeding Generative Art X, Milan, Italy. Дата обращения: 26 сентября 2016.
  81. ↑ Ouellette, Jennifer (November 2001). "Pollock's Fractals". Discover Magazine. Дата обращения: 26 сентября 2016.
  82. ↑ Galilei, Galileo. The Assayer. — 1623., as translated in Drake, Stillman. Discoveries and Opinions of Galileo. — Doubleday, 1957. — P. 237–238. — ISBN 0-385-09239-3.
  83. ↑ Cucker, Felix. Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. — Cambridge University Press, 2013. — P. 381. — ISBN 978-0-521-72876-8.
  84. ↑ Cucker, Felix. Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. — Cambridge University Press, 2013. — P. 10. — ISBN 978-0-521-72876-8.
  85. ↑ King, Jerry P. The Art of Mathematics. — Fawcett Columbine, 1992. — P. 8–9. — ISBN 0-449-90835-6.
  86. ↑ King, Jerry P. The Art of Mathematics. — Fawcett Columbine, 1992. — P. 135–139. — ISBN 0-449-90835-6.
  87. ↑ Devlin, Keith. Do Mathematicians Have Different Brains? // The Math Gene: How Mathematical Thinking Evolved And Why Numbers Are Like Gossip. — Basic Books, 2000. — P. 140. — ISBN 978-0-465-01619-8.
  88. ↑ англ. "Why are numbers beautiful? It's like asking why is Beethoven's Ninth Symphony beautiful. If you don't see why, someone can't tell you. I know numbers are beautiful."
  89. ↑ Wasilewska, Katarzyna Mathematics in the World of Dance. Bridges (2012). Дата обращения: 1 сентября 2015.
  90. ↑ 1 2 Malkevitch, Joseph Mathematics and Art. American Mathematical Society. Дата обращения: 1 сентября 2015.
  91. ↑ Malkevitch, Joseph Mathematics and Art. 2. Mathematical tools for artists. American Mathematical Society. Дата обращения: 1 сентября 2015.
  92. ↑ Math and Art: The Good, the Bad, and the Pretty. Mathematical Association of America. Дата обращения: 2 сентября 2015.
  93. ↑ Cohen, Louise How to spin the colour wheel, by Turner, Malevich and more. Tate Gallery (1 июля 2014). Дата обращения: 4 сентября 2015.
  94. ↑ Kemp, Martin. The Science of Art: Optical Themes in Western Art from Brunelleschi to Seurat. — Yale University Press, 1992. — ISBN 978-968-867-185-6.
  95. ↑ Gage, John. Color and Culture: Practice and Meaning from Antiquity to Abstraction. — University of California Press, 1999. — P. 207. — ISBN 978-0-520-22225-0.
  96. ↑ Malkevitch, Joseph Mathematics and Art. 3. Symmetry. American Mathematical Society. Дата обращения: 1 сентября 2015.
  97. ↑ Malkevitch, Joseph Mathematics and Art. 4. Mathematical artists and artist mathematicians. American Mathematical Society. Дата обращения: 1 сентября 2015.
  98. ↑ Wright, Richard (1988). "Some Issues in the Development of Computer Art as a Mathematical Art Form". Leonardo. 1 (Electronic Art, supplemental issue): 103—110. doi:10.2307/1557919. JSTOR 1557919.
  99. ↑ Kalajdzievski, Sasho. Math and Art: An Introduction to Visual Mathematics. — Chapman and Hall, 2008. — ISBN 978-1-58488-913-7.
  100. ↑ 1 2 Beddard, Honor Computer art at the V&A. Victoria and Albert Museum. Дата обращения: 22 сентября 2015.
  101. ↑ "Computer Does Drawings: Thousands of lines in each". The Guardian. 17 September 1962. in Beddard, 2015.
  102. ↑ O'Hanrahan, Elaine. Drawing Machines: The machine produced drawings of Dr. D. P. Henry in relation to conceptual and technological developments in machine-generated art (UK 1960–1968). Unpublished MPhil. Thesis.. — John Moores University, Liverpool, 2005. in Beddard, 2015.
  103. ↑ Bellos, Alex (24 February 2015). "Catch of the day: mathematician nets weird, complex fish". The Guardian. Дата обращения: 25 сентября 2015.
  104. ↑ "A Bird in Flight (2016)," by Hamid Naderi Yeganeh. American Mathematical Society (23 марта 2016). Дата обращения: 6 апреля 2017.
  105. ↑ Chung, Stephy (September 18, 2015). "Next da Vinci? Math genius using formulas to create fantastical works of art". CNN.
  106. ↑ Levin, Golan Generative Artists. CMUEMS (2013). Дата обращения: 27 октября 2015. This includes a link to Hvidtfeldts Syntopia.
  107. ↑ Verostko, Roman The Algorists. Дата обращения: 27 октября 2015.
  108. ↑ Cucker, Felix. Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. — Cambridge University Press, 2013. — P. 315–317. — ISBN 978-0-521-72876-8.
  109. ↑ Ошибка в сносках?: Неверный тег <ref>; для сносок Miller не указан текст
  110. ↑ Miller, Arthur I. Insights of Genius: Imagery and Creativity in Science and Art. — Springer, 2012. — ISBN 1-4612-2388-1.
  111. ↑ Henderson, Linda D. The Fourth Dimension and Non-Euclidean geometry in Modern Art. — Princeton University Press, 1983.
  112. ↑ Antliff, Mark. Cubism and Culture / Antliff, Mark, Leighten, Patricia Dee. — Thames & Hudson, 2001. (недоступная ссылка)
  113. ↑ Everdell, William R. The First Moderns: Profiles in the Origins of Twentieth-Century Thought. — University of Chicago Press, 1997. — P. 312. — ISBN 0-226-22480-5.
  114. ↑ Green, Christopher. Cubism and its Enemies, Modern Movements and Reaction in French Art, 1916–1928. — Yale University Press, 1987. — P. 13–47.
  115. ↑ Metzinger, Jean (October-November 1910). "Note sur la peinture". Pan: 60.{{cite journal}}: Википедия:Обслуживание CS1 (формат даты) (ссылка) in Miller. Einstein, Picasso. — Basic Books. — P. 167.
  116. ↑ Metzinger, Jean. Le cubisme était né. — Éditions Présence, 1972. — P. 43–44. in Ferry, Luc. Homo Aestheticus: The Invention of Taste in the Democratic Age. — University of Chicago Press, 1993. — P. 215. — ISBN 0-226-24459-8.
  117. ↑ Man Ray–Human Equations A Journey from Mathematics to Shakespeare. February 7 – May 10, 2015. Phillips Collection. Дата обращения: 5 сентября 2015.
  118. ↑ Adcock, Craig (1987). "Duchamp's Eroticism: A Mathematical Analysis". Iowa Research Online. 16 (1): 149—167.
  119. ↑ Elder, R. Bruce. DADA, Surrealism, and the Cinematic Effect. — Wilfrid Laurier University Press, 2013. — P. 602. — ISBN 978-1-55458-641-7.
  120. ↑ Tubbs, Robert. Mathematics in Twentieth-Century Literature and Art: Content, Form, Meaning. — JHU Press, 2014. — P. 118. — ISBN 978-1-4214-1402-7.
  121. ↑ Hiroshi Sugimoto Conceptual Forms and Mathematical Models February 7 – May 10, 2015. Phillips Collection. Дата обращения: 5 сентября 2015.
Источник — https://ru.wikipedia.org/w/index.php?title=Математика_и_изобразительное_искусство&oldid=85849773