Логнормальное распределение

Логнормальное
μ=0Плотность вероятности
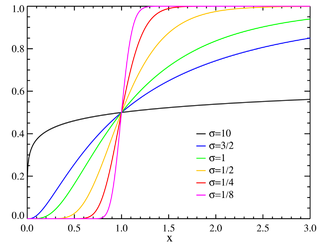μ=0Функция распределения
Обозначение	$\ln N(\mu ,\sigma ^{2})$, $LN(\mu ,\sigma ^{2})$
Параметры	$\sigma >0$ $-\infty <\mu <\infty$
Носитель	$x\in (0;+\infty )$
Плотность вероятности	$\exp \left(-\left.\left[{\frac {\ln(x)-\mu }{\sigma }}\right]^{2}\right/2\right)\left/\left(x\sigma {\sqrt {2\pi }}\right)\right.$
Функция распределения	${\frac {1}{2}}+{\frac {1}{2}}\mathrm {erf} \left[{\frac {\ln(x)-\mu }{\sigma {\sqrt {2}}}}\right]$
Математическое ожидание	$e^{\mu +\sigma ^{2}/2}$
Медиана	$e^{\mu }$
Мода	$e^{\mu -\sigma ^{2}}$
Дисперсия	$(e^{\sigma ^{2}}\!\!-1)e^{2\mu +\sigma ^{2}}$
Коэффициент асимметрии	$(e^{\sigma ^{2}}\!\!+2){\sqrt {e^{\sigma ^{2}}\!\!-1}}$
Коэффициент эксцесса	$e^{4\sigma ^{2}}\!\!+2e^{3\sigma ^{2}}\!\!+3e^{2\sigma ^{2}}\!\!-6$
Дифференциальная энтропия	${\frac {1}{2}}+{\frac {1}{2}}\ln(2\pi \sigma ^{2})+\mu$
Производящая функция моментов	$\operatorname {E} [X^{s}]=e^{s\mu +{\tfrac {1}{2}}s^{2}\sigma ^{2}}.$
Характеристическая функция	$\sum _{n=0}^{\infty }{\frac {(it)^{n}}{n!}}e^{n\mu +n^{2}\sigma ^{2}/2}$

Логнорма́льное распределе́ние (логарифмически-нормальное) в теории вероятностей — это двухпараметрическое семейство абсолютно непрерывных распределений. Если случайная величина имеет логнормальное распределение, то её логарифм имеет нормальное распределение.

Определение

Пусть распределение случайной величины $X$ задаётся плотностью вероятности, имеющей вид:

$$f_{X}(x)={\frac {1}{x\sigma {\sqrt {2\pi }}}}e^{-(\ln x-\mu )^{2}/2\sigma ^{2}},$$

где $x>0,\;\sigma >0,\;\mu \in \mathbb {R}$. Тогда говорят, что $X$ имеет логнормальное распределение с параметрами $\mu$ и $\sigma$. Пишут: $X\sim \mathrm {LogN} (\mu ,\sigma ^{2})\$.

Моменты

Формула для $k$-го момента логнормальной случайной величины $X$ имеет вид:

$\mathbb {E} \left[X^{k}\right]=e^{k\mu +{\frac {k^{2}\sigma ^{2}}{2}}},\;k\in \mathbb {N} ,$

откуда, в частности:

• $\mathbb {E} [X]=e^{\mu +{\sigma ^{2} \over 2}}$ — математическое ожидание,
• $\mathrm {D} [X]=\left(e^{\sigma ^{2}}-1\right)e^{2\mu +\sigma ^{2}}$ — дисперсия,
• Асимметрия всегда положительна.

Любые нецентральные моменты n-мерного совместного логнормального распределения могут быть вычислены по простой формуле:

$\alpha _{n}=e^{(\mu ,n)+{\frac {1}{2}}(n,\Sigma n)}$, где $\mu$ и $\Sigma$ — параметры многомерного совместного распределения. $n$ — вектор, компоненты которого задают порядок момента. (Например, в двухмерном случае, $n=(2,0)$ — второй нецентральный момент первой компоненты, $n=(1,1)$ — смешанный второй момент). Круглые скобки обозначают скалярное произведение.

Свойства логнормального распределения

• Если $X_{1},\ldots ,X_{n}$ — независимые логнормальные случайные величины, такие что $X_{i}\sim \mathrm {LogN} (\mu ,\sigma _{i}^{2})$, то их произведение также логнормально:

  $Y=\prod \limits _{i=1}^{n}X_{i}\sim \mathrm {LogN} \left(n\mu ,\sum \limits _{i=1}^{n}\sigma _{i}^{2}\right)$.

Связь с другими распределениями

• Если $X\sim \mathrm {LogN} (\mu ,\sigma ^{2})\$, то $Y=\ln(X)\sim \mathrm {N} (\mu ,\sigma ^{2})\$.

И наоборот, если $Y\sim \mathrm {N} (\mu ,\sigma ^{2})\$, то $X=\exp(Y)\sim \mathrm {LogN} (\mu ,\sigma ^{2})\$.

Моделирование логнормальных случайных величин

Для моделирования обычно используется связь с нормальным распределением. Поэтому, достаточно сгенерировать нормально распределённую случайную величину, например, используя преобразование Бокса — Мюллера, и вычислить её экспоненту.

Вариации и обобщения

Одним из возможных обобщений является усечённое логнормальное распределение, описываемое плотностью вероятности:

$f_{X}(x)={\frac {1}{(x-\gamma )\sigma {\sqrt {2\pi }}}}e^{-(\ln(x-\gamma )-\mu )^{2}/2\sigma ^{2}},$

где $0<\gamma <x$.

Приложения

Логнормальное распределение часто возникает в природе и широко используется для описания разных параметров в различных дисциплинах. Например, в медицине его могут применять для инкубационных периодов случаев какого-либо заболевания, в геологии — для концентрации редких элементов в горных породах, в лингвистике — для количества слов в предложениях. Распределение частиц по размерам в разных системах также часто оказывается близко к логнормальному. Однако здесь есть исключения, например, распределение астероидов по размерам в Солнечной системе подчиняется степенному закону.

Литература

• Crow, Edwin L.; Shimizu, Kunio (1988), Lognormal Distributions, Theory and Applications, Statistics: Textbooks and Monographs, vol. 88, New York: Marcel Dekker, Inc., pp. xvi+387, ISBN 0-8247-7803-0, MR 0939191, Zbl 0644.62014
• Aitchison, J. and Brown, J.A.C. (1957) The Lognormal Distribution, Cambridge University Press.
• Eric W. Weisstein et al. Log Normal Distribution at MathWorld. Electronic document, retrieved October 26, 2006.
• Holgate, P. The lognormal characteristic function (неопр.) // Communications in Statistics - Theory and Methods. — 1989. — Т. 18, № 12. — С. 4539—4548. — doi:10.1080/03610928908830173.
• Brooks, Robert; Corson, Jon; Donal, Wales The Pricing of Index Options When the Underlying Assets All Follow a Lognormal Diffusion (англ.) // Advances in Futures and Options Research : journal. — 1994. — Vol. 7.