Распределение Стьюдента
| Распределение Стьюдента | |
|---|---|
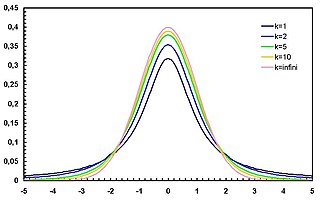 Плотность вероятности Плотность вероятности | |
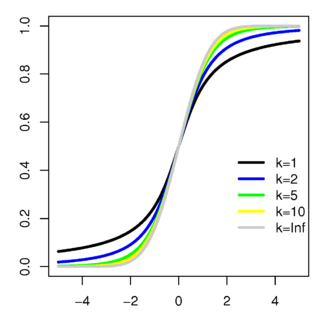 Функция распределения Функция распределения | |
| Обозначение | |
| Параметры | — число степеней свободы |
| Носитель | |
| Плотность вероятности | |
| Функция распределения | где — гипергеометрическая функция |
| Математическое ожидание | , если |
| Медиана | |
| Мода | |
| Дисперсия | , если |
| Коэффициент асимметрии | , если |
| Коэффициент эксцесса | , если |
| Дифференциальная энтропия |
|
| Производящая функция моментов | не определена |
Распределе́ние Стью́дента (-распределение) в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений. Уильям Сили Госсет (1876—1937) первым опубликовал работы, посвящённые этому распределению, под псевдонимом «Стьюдент».
Распределение Стьюдента играет важную роль в статистическом анализе и используется, например, в t-критерии Стьюдента для оценки статистической значимости разности двух выборочных средних, при построении доверительного интервала для математического ожидания нормальной совокупности при неизвестной дисперсии, а также в линейном регрессионном анализе. Распределение Стьюдента также появляется в байесовском анализе данных, распределённых по нормальному закону.
График плотности распределения Стьюдента, как и нормального распределения, является симметричным и имеет вид колокола, но с более «тяжёлыми» хвостами, то есть реализациям случайной величины, имеющей распределение Стьюдента, более свойственно сильно отличаться от математического ожидания. Это делает его важным для понимания статистического поведения определённых типов отношений случайных величин, в которых отклонение в знаменателе увеличено и может производить отдалённые величины, когда знаменатель соотношения близок к нулю.
Распределение Стьюдента — частный случай обобщённого гиперболического распределения.
История и этимология
[править | править код]В статистике t-распределение было впервые получено как апостериорное распределение в 1876 году Фридрихом Гельмертом[1][2][3] и Якобом Люротом[англ.][4][5][6].
В англоязычной литературе распределение берёт название из статьи Уильяма Госсета в журнале Пирсона «Биометрика», опубликованной под псевдонимом «Стьюдент»[7][8].
Госсет работал в пивоварне Гиннесс в Дублине, Ирландия, и применял свои знания в области статистики как при варке пива, так и на полях — для выведения самого урожайного сорта ячменя. Исследования были обращены к нуждам пивоваренной компании и проводились на малом количестве наблюдений, что послужило толчком для развития методов, работающих на малых выборках.
Госсету пришлось скрывать свою личность при публикации из-за того, что ранее другой исследователь, работавший на Гиннесс, опубликовал в своих материалах сведения, составлявшие коммерческую тайну компании, после чего Гиннесс запретил своим работникам публикацию любых материалов, независимо от содержавшейся в них информации.
Статья Госсета описывает распределение как «Частотное распределение стандартных отклонений выборок, извлечённых из генеральной совокупности». Оно стало известным благодаря работе Роналда Фишера, который называл распределение «распределением Стьюдента», а величину — буквой t[9].
Определение
[править | править код]Пусть — независимые стандартные нормальные случайные величины, такие что . Тогда распределение случайной величины , где
называется распределением Стьюдента с степенями свободы .
Это распределение абсолютно непрерывно с плотностью:
- ,
где — гамма-функция Эйлера. Таким образом:
- для чётных
и соответственно
- для нечётных .
Также плотность распределения Стьюдента можно выразить воспользовавшись бета-функцией Эйлера :
- .
График функции плотности t-распределения симметричен, а его форма напоминает форму колокола, как у стандартного нормального распределения, но он ниже и шире.
Следующие графики отражают плотность t-распределения при увеличении числа степеней свободы. Можно наблюдать как по мере возрастания , кривая функции плотности все больше напоминает стандартное нормальное распределение.
Функция распределения
[править | править код]Функция распределения может быть выражена через регуляризованную неполную бета-функцию . Для ,
- где [10]
Для значения можно получить в силу симметричности распределения.
Другая формула верна для [10]:
- ,
где 2F1 является частным случаем гипергеометрической функции.
Частные случаи
[править | править код]- Распределение Стьюдента с одной степенью свободы () это стандартное распределение Коши.
- Функция распределения:
- Плотность вероятности:
- Распределение Стьюдента с двумя степенями свободы ():
- Функция распределения:
- Плотность вероятности: ;
- Распределение Стьюдента с тремя степенями свободы ():
- Плотность вероятности:
- Распределение Стьюдента с бесконечным числом степеней свободы ():
- Плотность вероятности
совпадает с плотностью вероятности стандартного нормального распределения.
Свойства распределения Стьюдента
[править | править код]- Распределение Стьюдента симметрично. В частности если , то .
- Существуют только моменты порядка , и не существуют моменты порядка . При этом все существующие моменты нечетного порядка равны нулю.
- , если нечётно;
- , если чётно. В частности,
- Математическое ожидание , если .
- Дисперсия , если .
Характеристики
[править | править код]Распределение Стьюдента с степенями свободы может быть определено как распределение случайной величины [10][11]
- ,
где
- Z — случайная величина, имеющая стандартное нормальное распределение ;
- V — случайная величина, имеющая распределение хи-квадрат с степенями свободы;
- Z и V — независимые случайные величины .
Пусть, , независимые случайные величины, имеющие нормальное распределение ,
— выборочное среднее,
- — несмещённая оценка дисперсии.
Тогда случайная величина
имеет распределение хи-квадрат с степенями свободы[12].
Случайная величина имеет стандартное нормальное распределение, , так как выборочное среднее имеет нормальное распределение . Более того, можно показать, что эти две случайные величины (нормальная и хи-квадрат ) независимы.
Подставим получившиеся величины в величину
- ,
которая имеет распределение Стьюдента и отличается от тем, что стандартное отклонение заменено случайной величиной , . Заметим, что неизвестная дисперсия не появляется в , так как она была и в числителе, и в знаменателе. Госсет интуитивно получил плотность вероятности, установленную выше, где соответствует ; Фишер доказал это в 1925 году[9].
Распределение статистики критерия , зависит от , но не зависит от μ или σ2, что и делает распределение важным как в теории, так и на практике.
Как возникает t-распределение
[править | править код]Выборочная дисперсия
[править | править код]Распределение Стьюдента возникает в связи с распределением выборочной дисперсии. Пусть независимые случайные величины, такие что . Обозначим выборочное среднее этой выборки, а её выборочную дисперсию. Тогда
- .
С этим фактом связано использование распределения Стьюдента в статистике для точечного оценивания, построения доверительных интервалов и тестирования гипотез, касающихся неизвестного среднего выборки из нормального распределения.
Байесовская статистика
[править | править код]В байесовской статистике, нецентральное t-распределение встречается как маргинальное распределение коэффициента нормального распределения .
Зависимость неизвестной дисперсии выражается через:
где — это данные {xi}, а представляет собой любую другую информацию, которая могла быть использована для создания модели.
Когда данные неинформативны из теоремы Байеса следует
нормальное распределение и масштабированное обратное хи-квадрат распределение, где
- .
Маргинализованный интеграл в таком случае имеет вид
после замены , где ,
получим
и оценку
теперь стандартный Гамма интеграл, который оценивается константой
это нестандартизированное t-распределение.
С помощью замены получаем стандартизированное t-распределение.
Дифференцирование выше было представлено для случая неинформативной априорной вероятности для и ; но очевидно, что любая априорная вероятность, ведет к смешению нормального распределения и масштабированного обратного хи-квадрат распределение, что нецентральному t-распределению с масштабированием и смещением на , параметр масштабирования будет в находиться под влиянием априорной информации и данных, а не только данных, как в примере выше.
Обобщения распределения Стьюдента
[править | править код]Нестандартизированное распределение Стьюдента
[править | править код]Распределение Стьюдента можно обобщить до семейства функций с тремя параметрами, включающими коэффициент сдвига и коэффициент масштаба , через отношение
или
- ,
где классическое распределение Стьюдента с степенями свободы.
Плотность нестандартизированного распределения Стьюдента представляет собой репараметризованное распределение Пирсона типа VII и определяется следующим выражением[13]
Здесь не является стандартным отклонением, как в нормальном распределении, это, вообще говоря, другой параметр масштаба. Однако при плотность распределения Пирсона типа VII стремится к плотности нормального распределения со стандартным отклонением .
В байесовском выводе предельное распределение неизвестного среднего значения выше чем , и соответствует , где
для ,
для
Такое распределение является результатом комбинации распределения Гаусса (нормального распределения) со средним значением и неизвестной дисперсией, с обратным гамма-распределением, с дисперсией, имеющей параметры и . Другими словами, предполагается, что случайная величина X обладает нормальным распределением с неизвестной дисперсией, распределенной как обратная гамма, а затем дисперсия исключается. Такое свойство полезно из-за того, что обратное гамма-распределение — это сопряженное априорное распределение дисперсии распределения Гаусса, именно поэтому нестандартизированное распределение Стьюдента естественным образом возникает во многих байесовских задачах.
Эквивалентно, это распределение является результатом комбинации распределения Гаусса с масштабированным обратным хи-квадрат распределением с параметрами and . Масштабированное обратное хи-квадрат распределение — точно то же самое распределение, что и обратное гамма-распределение, но с другой параметризацией, а именно .
Альтернативная параметризация на основании обратного параметра масштабирования λ[14] (аналогично тому, как мера точности обратна дисперсии), определенная отношением ,
тогда плотность определяется как
Свойства:
для ,
для
Это распределение является результатом комбинации распределения Гаусса со средним и неизвестной мерой точности (обратной дисперсии), с гамма-распределением с параметрами and . Другими словами, предполагается, что случайная величина X обладает нормальным распределением с неизвестной гамма-распределённой мерой точности.
Нецентральное распределение Стьюдента
[править | править код]Нецентральное распределение Стьюдента, это один способов обобщения стандартного распределения Стьюдента, включающий дополнительный коэффициент сдвига (параметр нецентральности) .
В нецентральном распределении Стьюдента медиана не совпадает с модой, то есть оно не симметрично (в отличие от нестандартизированного).
Это распределение важно для изучения статистической мощности t-критерия Стьюдента.
Дискретное распределение Стьюдента
[править | править код]Дискретное распределение Стьюдента имеет следующую функцию распределения с r пропорциональным:[15]
Где a, b, и k — параметры. Такое распределение возникает при работе с системами из дискретных распределений, таких как распределение Пирсона.[16]
Связь с другими распределениями
[править | править код]- Распределение Стьюдента является распределением Пирсона типа VII[17].
- Распределение Стьюдента с одной степенью свободы () это стандартное распределение Коши: .
- Распределение Стьюдента сходится к стандартному нормальному при . Пусть дана последовательность случайных величин , где . Тогда: по распределению при .
- Квадрат случайной величины, имеющей распределение Стьюдента, также имеет распределение Фишера. Пусть . Тогда: .
Обобщение распределения Гаусса
[править | править код]Мы можем получить выборку с t-распределением, взяв отношение величин из нормального распределения и квадратный корень из распределения хи-квадрат.
где — независимые стандартные нормальные случайные величины, такие что
Если мы вместо нормального распределения, возьмём например, Ирвин-Холл, получится симметричное распределение с 4 параметрами, которое включает в себя нормальное, равномерное, треугольное, а также распределения Стьюдента и Коши; таким образом, это обобщение более гибкое, чем многие другие симметричные обобщения распределения Гаусса.
Применение распределения Стьюдента
[править | править код]Проверка гипотезы
[править | править код]Некоторые статистики могут иметь распределение Стьюдента на выборках небольшого размера, поэтому распределение Стьюдента формирует основу критериев значимости. Например, тест ранговой корреляции Спирмена ρ, в нулевом случае (нулевая корреляция) хорошо аппроксимируется распределением Стьюдента при размере выборки больше 20.
Построение доверительного интервала
[править | править код]Распределение Стьюдента может быть использовано для оценки того, насколько вероятно, что истинное среднее находится в каком-либо заданном диапазоне.
Предположим, что число A выбрано так, что
.
Тогда T имеет t-распределение с n-1 степенями свободы. В силу симметрии распределения, это равноценно утверждению, что А удовлетворяет
или , тогда
что эквивалентно
таким образом, интервал с доверительным пределом в точках — это 90 % доверительный интервал для μ. Следовательно, если мы находим среднее множества наблюдений (нормально распределённых), мы можем использовать распределение Стьюдента, чтобы определить, включают ли доверительные пределы по этому среднему какое-либо теоретически предсказанное значение, например, значение, предсказанное, исходя из нулевой гипотезы.
Такой подход применяется в t-критерии Стьюдента: если разность между средними значениями выборок из двух нормальных распределений сама может быть нормально распределена, распределение Стьюдента может быть использовано для исследования того, можно ли с большой долей вероятности полагать эту разность равной нулю.
Для нормально распределённых выборок односторонний (1−a) верхний доверительный предел (UCL) среднего значения равен
.
Полученный в результате верхний доверительный предел будет наибольшим средним значением для данного доверительного интервала и размера выборки. Другими словами, если среднее значение множества наблюдений, вероятность того, что среднее значение распределения уступает равна уровню значимости 1-a.
Построение интервала-предиктора
[править | править код]Распределение Стьюдента может быть использовано для получения интервала-предиктора для ненаблюдаемой выборки из нормального распределения с неизвестным средним и дисперсией.
В байесовской статистике
[править | править код]Распределение Стьюдента, особенно нецентральное, часто возникает в байесовской статистике как результат связи с нормальным распределением.
Действительно, если нам неизвестна дисперсия нормально распределенной случайной величины, но известно сопряженное априорное распределение, можно будет подобрать такое гамма-распределение, что полученные в результате величины будут обладать распределением Стьюдента.
Эквивалентные конструкции с теми же результатами включают сопряжённое масштабированное обратное хи-квадратное распределение. Если некорректное априорное распределение, пропорциональное , расположено над дисперсией, то также возникает распределение Стьюдента. Это происходит независимо от того, известно ли среднее нормально распределенной величины, распределённое с сопряжённым априорным распределением, или нет.
Параметрическое моделирование, устойчивое к нарушениям исходных предпосылок
[править | править код]Распределение Стьюдента часто используется в качестве альтернативы нормальному распределению для модели данных.[18] Это происходит из-за того, что довольно часто настоящие данные имеют более тяжелые хвосты, чем позволяет нормальное распределение. Классический подход заключается в определении выбросов и их исключении (или понижении их веса). Однако не всегда легко определить выброс (особенно в задачах с большой размерностью), и распределение Стьюдента является естественным выбором, обеспечивающим параметрический подход к робастной статистике.
Ланж и другие исследовали использование распределения Стьюдента для робастного (устойчивого к нарушениям исходных предпосылок) моделирования данных. Байесовский расчет обнаруживается у Гельмана и др.
Количество степеней свободы контролирует эксцесс распределения и коррелируется с параметром масштабирования.
Некоторые другие свойства распределения Стьюдента
[править | править код]Пусть, — интеграл функции плотности вероятности Стьюдента, — вероятность того, что значение t, меньше, чем значение, рассчитанное по данным наблюдений.
Функция может быть использована для тестировании того, является ли разница между средними значениями двух наборов данных взятых из одной совокупности, статистически значимой, это достигается путём вычисления соответствующего значения t и вероятности его возникновения.
Это используется например, в T-критерии Стьюдента. Для t-распределения с степенями свободы, — вероятность того, что t будет меньше наблюдаемого значения, если два средних значения были одинаковыми. Его можно легко вычислить из кумулятивной функции распределения распределения Стьюдента:
где Ix — регуляризированная неполная бета функция (a, b).
При статистической проверки гипотез эта функция используется для построения р-значения.
Выборка по методу Монте-Карло
[править | править код]Есть разные подходы к получению случайных величин из распределения Стьюдента. Всё зависит от того, требуются независимые выборки, или они могут быть построены путём применения обратной функции распределения над выборкой с однородным распределением.
В случае с независимой выборкой легко применить расширение метода Бокса-Мюллера в его полярной (тригонометрической) форме[19]. Преимущество этого метода в том, что он одинаково относится ко всем положительным степеням свободы , в то время как многие другие методы не будут работать, если близка к нулю.[19]
Плотность распределения Стьюдента через решение дифференциального уравнения
[править | править код]Плотность распределения Стьюдента можно получить, решив следующее дифференциальное уравнение:
Процентили
[править | править код]Таблицы значений
[править | править код]Многие учебники по статистике включают в себя таблицы распределения Стьюдента.
В наши дни лучший способ узнать полностью точное критическое значение t или кумулятивную вероятность — это использование статистической функции, встроенной в электронные таблицы (Office Excel, OpenOffice Calc и т. д.), или интерактивного веб-калькулятора. Нужные функции электронных таблиц — TDIST и TINV.
Таблица ниже включает в себя значения некоторых значений для распределений Стьюдента с v степенями свободы для ряда односторонних или двусторонних критических областей.
В качестве примера того, как читать эту таблицу, возьмём четвёртый ряд, который начинается с 4; это означает, что v, количество степеней свободы, равно 4 (и если мы работаем, как это показано выше, с n величин с фиксированной суммой, то n = 5). Возьмём пятое значение в колонке 95 % для односторонних(90 % для двусторонних). Значение это равно «2.132». Значит, вероятность, что T меньше 2.132 равна 95 % или Pr(−∞ <T< 2.132) = 0.95; это также означает, что Pr(−2.132 <T< 2.132) = 0.9.
Это может быть вычислено по симметрии распределения,
- Pr(T < −2.132) = 1 − Pr(T > −2.132) = 1 − 0.95 = 0.05,
получаем
- Pr(−2.132 < T < 2.132) = 1 − 2(0.05) = 0.9.
Обратите внимание, что последний ряд также даёт критические точки: распределение Стьюдента с бесконечным количеством степеней — это нормальное распределение.
Первая колонка отображает число степеней свободы.
| односторонний | 75 % | 80 % | 85 % | 90 % | 95 % | 97.5 % | 99 % | 99.5 % | 99.75 % | 99.9 % | 99.95 % |
|---|---|---|---|---|---|---|---|---|---|---|---|
| двусторонний | 50 % | 60 % | 70 % | 80 % | 90 % | 95 % | 98 % | 99 % | 99.5 % | 99.8 % | 99.9 % |
| 1 | 1.000 | 1.376 | 1.963 | 3.078 | 6.314 | 12.71 | 31.82 | 63.66 | 127.3 | 318.3 | 636.6 |
| 2 | 0.816 | 1.080 | 1.386 | 1.886 | 2.920 | 4.303 | 6.965 | 9.925 | 14.09 | 22.33 | 31.60 |
| 3 | 0.765 | 0.978 | 1.250 | 1.638 | 2.353 | 3.182 | 4.541 | 5.841 | 7.453 | 10.21 | 12.92 |
| 4 | 0.741 | 0.941 | 1.190 | 1.533 | 2.132 | 2.776 | 3.747 | 4.604 | 5.598 | 7.173 | 8.610 |
| 5 | 0.727 | 0.920 | 1.156 | 1.476 | 2.015 | 2.571 | 3.365 | 4.032 | 4.773 | 5.893 | 6.869 |
| 6 | 0.718 | 0.906 | 1.134 | 1.440 | 1.943 | 2.447 | 3.143 | 3.707 | 4.317 | 5.208 | 5.959 |
| 7 | 0.711 | 0.896 | 1.119 | 1.415 | 1.895 | 2.365 | 2.998 | 3.499 | 4.029 | 4.785 | 5.408 |
| 8 | 0.706 | 0.889 | 1.108 | 1.397 | 1.860 | 2.306 | 2.896 | 3.355 | 3.833 | 4.501 | 5.041 |
| 9 | 0.703 | 0.883 | 1.100 | 1.383 | 1.833 | 2.262 | 2.821 | 3.250 | 3.690 | 4.297 | 4.781 |
| 10 | 0.700 | 0.879 | 1.093 | 1.372 | 1.812 | 2.228 | 2.764 | 3.169 | 3.581 | 4.144 | 4.587 |
| 11 | 0.697 | 0.876 | 1.088 | 1.363 | 1.796 | 2.201 | 2.718 | 3.106 | 3.497 | 4.025 | 4.437 |
| 12 | 0.695 | 0.873 | 1.083 | 1.356 | 1.782 | 2.179 | 2.681 | 3.055 | 3.428 | 3.930 | 4.318 |
| 13 | 0.694 | 0.870 | 1.079 | 1.350 | 1.771 | 2.160 | 2.650 | 3.012 | 3.372 | 3.852 | 4.221 |
| 14 | 0.692 | 0.868 | 1.076 | 1.345 | 1.761 | 2.145 | 2.624 | 2.977 | 3.326 | 3.787 | 4.140 |
| 15 | 0.691 | 0.866 | 1.074 | 1.341 | 1.753 | 2.131 | 2.602 | 2.947 | 3.286 | 3.733 | 4.073 |
| 16 | 0.690 | 0.865 | 1.071 | 1.337 | 1.746 | 2.120 | 2.583 | 2.921 | 3.252 | 3.686 | 4.015 |
| 17 | 0.689 | 0.863 | 1.069 | 1.333 | 1.740 | 2.110 | 2.567 | 2.898 | 3.222 | 3.646 | 3.965 |
| 18 | 0.688 | 0.862 | 1.067 | 1.330 | 1.734 | 2.101 | 2.552 | 2.878 | 3.197 | 3.610 | 3.922 |
| 19 | 0.688 | 0.861 | 1.066 | 1.328 | 1.729 | 2.093 | 2.539 | 2.861 | 3.174 | 3.579 | 3.883 |
| 20 | 0.687 | 0.860 | 1.064 | 1.325 | 1.725 | 2.086 | 2.528 | 2.845 | 3.153 | 3.552 | 3.850 |
| 21 | 0.686 | 0.859 | 1.063 | 1.323 | 1.721 | 2.080 | 2.518 | 2.831 | 3.135 | 3.527 | 3.819 |
| 22 | 0.686 | 0.858 | 1.061 | 1.321 | 1.717 | 2.074 | 2.508 | 2.819 | 3.119 | 3.505 | 3.792 |
| 23 | 0.685 | 0.858 | 1.060 | 1.319 | 1.714 | 2.069 | 2.500 | 2.807 | 3.104 | 3.485 | 3.767 |
| 24 | 0.685 | 0.857 | 1.059 | 1.318 | 1.711 | 2.064 | 2.492 | 2.797 | 3.091 | 3.467 | 3.745 |
| 25 | 0.684 | 0.856 | 1.058 | 1.316 | 1.708 | 2.060 | 2.485 | 2.787 | 3.078 | 3.450 | 3.725 |
| 26 | 0.684 | 0.856 | 1.058 | 1.315 | 1.706 | 2.056 | 2.479 | 2.779 | 3.067 | 3.435 | 3.707 |
| 27 | 0.684 | 0.855 | 1.057 | 1.314 | 1.703 | 2.052 | 2.473 | 2.771 | 3.057 | 3.421 | 3.690 |
| 28 | 0.683 | 0.855 | 1.056 | 1.313 | 1.701 | 2.048 | 2.467 | 2.763 | 3.047 | 3.408 | 3.674 |
| 29 | 0.683 | 0.854 | 1.055 | 1.311 | 1.699 | 2.045 | 2.462 | 2.756 | 3.038 | 3.396 | 3.659 |
| 30 | 0.683 | 0.854 | 1.055 | 1.310 | 1.697 | 2.042 | 2.457 | 2.750 | 3.030 | 3.385 | 3.646 |
| 40 | 0.681 | 0.851 | 1.050 | 1.303 | 1.684 | 2.021 | 2.423 | 2.704 | 2.971 | 3.307 | 3.551 |
| 50 | 0.679 | 0.849 | 1.047 | 1.299 | 1.676 | 2.009 | 2.403 | 2.678 | 2.937 | 3.261 | 3.496 |
| 60 | 0.679 | 0.848 | 1.045 | 1.296 | 1.671 | 2.000 | 2.390 | 2.660 | 2.915 | 3.232 | 3.460 |
| 80 | 0.678 | 0.846 | 1.043 | 1.292 | 1.664 | 1.990 | 2.374 | 2.639 | 2.887 | 3.195 | 3.416 |
| 100 | 0.677 | 0.845 | 1.042 | 1.290 | 1.660 | 1.984 | 2.364 | 2.626 | 2.871 | 3.174 | 3.390 |
| 120 | 0.677 | 0.845 | 1.041 | 1.289 | 1.658 | 1.980 | 2.358 | 2.617 | 2.860 | 3.160 | 3.373 |
| ∞ | 0.674 | 0.842 | 1.036 | 1.282 | 1.645 | 1.960 | 2.326 | 2.576 | 2.807 | 3.090 | 3.291 |
Например, если нам дана выборка с выборочной дисперсией 2 и выборочным средним 10, взятая из выборочного набора 11 (10 степеней свободы), используя формулу
Мы можем определить с 90 % уровнем доверия, что истинное среднее таково:
(то есть, в среднем, в 90 % случаев верхний предел превышает истинное среднее)
и, всё также с 90 % уверенностью, мы находим истинное среднее значение, превышающее
(В среднем, в 90 % случаев нижний предел меньше истинного среднего)
Так что с 80 % уверенностью (1-2*(1-90 %) = 80 %), мы находим истинное значение, лежащее в интервале
Другими словами, в 80 % случаев истинное среднее ниже верхнего предела и выше нижнего предела.
Это не эквивалентно утверждению, что с 80 % вероятностью истинное среднее лежит между определенной парой верхних и нижних пределов.
Обобщение
[править | править код]Обобщением распределения Стьюдента является обобщённое гиперболическое распределение.
Примечания
[править | править код]- ↑ Helmert, F. R. (1875). "Über die Bestimmung des wahrscheinlichen Fehlers aus einer endlichen Anzahl wahrer Beobachtungsfehler". Z. Math. Phys., 20, 300–3.
- ↑ Helmert, F. R. (1876a). "Über die Wahrscheinlichkeit der Potenzsummen der Beobachtungsfehler und uber einige damit in Zusammenhang stehende Fragen". Z. Math. Phys., 21, 192–218.
- ↑ Helmert, F. R. (1876b). "Die Genauigkeit der Formel von Peters zur Berechnung des wahrscheinlichen Beobachtungsfehlers directer Beobachtungen gleicher Genauigkeit", Astron. Nachr., 88, 113–32.
- ↑ Lüroth, J. Vergleichung von zwei Werten des wahrscheinlichen Fehlers (нем.) // Astron. Nachr. : magazin. — 1876. — Bd. 87, Nr. 14. — S. 209—220. — doi:10.1002/asna.18760871402. — .
- ↑ Pfanzagl, J.; Sheynin, O. A forerunner of the t-distribution (Studies in the history of probability and statistics XLIV) (англ.) // Biometrika : journal. — 1996. — Vol. 83, no. 4. — P. 891—898. — doi:10.1093/biomet/83.4.891.
- ↑ Sheynin, O. Helmert’s work in the theory of errors (англ.) // Arch. Hist. Exact Sci. : journal. — 1995. — Vol. 49. — P. 73—104. — doi:10.1007/BF00374700.
- ↑ “Student” [ William Sealy Gosset ]. The probable error of a mean (англ.) // Biometrika : journal. — 1908. — March (vol. 6, no. 1). — P. 1—25. — doi:10.1093/biomet/6.1.1. Архивировано 8 марта 2008 года.
- ↑ «Student» (William Sealy Gosset), original Biometrika paper as a scan Архивная копия от 5 марта 2016 на Wayback Machine
- ↑ 1 2 Рональд Фишер. Applications of “Student’s” distribution (англ.) // metron. — 1925. — Vol. 5. — P. 90—104. Архивировано 5 марта 2016 года.
- ↑ 1 2 3 Johnson, N.L., Kotz, S., Balakrishnan, N. глава 28 // Continuous Univariate Distributions, Volume 2, 2nd Edition.. — 1995. — ISBN 0-471-58494-0.
- ↑ Hogg & Craig (1978, Sections 4.4 and 4.8.)
- ↑ W. G. Cochran. The distribution of quadratic forms in a normal system, with applications to the analysis of covariance // Mathematical Proceedings of the Cambridge Philosophical Society. — 1934-04-01. — Т. 30, вып. 02. — С. 178—191. — ISSN 1469-8064. — doi:10.1017/S0305004100016595.
- ↑ Simon Jackman. Bayesian Analysis for the Social Sciences. — Wiley. — 2009. — С. 507.
- ↑ Bishop C.M. Pattern recognition and machine learning. — Springer. — 2006.
- ↑ Ord, J.K. (1972) Families of Frequency Distributions, Griffin. ISBN 0-85264-137-0 (Table 5.1)
- ↑ Ord, J.K. (1972) Families of Frequency Distributions, Griffin. ISBN 0-85264-137-0 (Chapter 5)
- ↑ Королюк, 1985, с. 134.
- ↑ Kenneth L. Lange, Roderick J. A. Little, Jeremy M. G. Taylor. Robust Statistical Modeling Using the t Distribution // Journal of the American Statistical Association. — 1989-12-01. — Т. 84, вып. 408. — С. 881—896. — ISSN 0162-1459. — doi:10.1080/01621459.1989.10478852.
- ↑ 1 2 Ralph W. Bailey. Polar Generation of Random Variates with the t-Distribution // Mathematics of Computation. — 1994-01-01. — Т. 62, вып. 206. — С. 779—781. — doi:10.2307/2153537. Архивировано 3 апреля 2016 года.
Литература
[править | править код]- Королюк В. С., Портенко Н. И., Скороход А. В., Турбин А. Ф. Справочник по теории вероятностей и математической статистике. — М.: Наука, 1985. — 640 с.














![{\displaystyle {\begin{matrix}{\frac {n+1}{2}}\left[\psi ({\frac {1+n}{2}})-\psi ({\frac {n}{2}})\right]\\[0.5em]+\log {\left[{\sqrt {n}}B({\frac {n}{2}},{\frac {1}{2}})\right]}\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1cd3fdc61973f68042141bd52ef3b36cd233e8a0)








































![{\displaystyle \mathbb {E} \left[t^{k}\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/03e22470d6afaa3397555bea76f3fecd20968fad)

![{\displaystyle \mathbb {E} \left[t^{k}\right]={\frac {1}{{\sqrt {\pi }}\Gamma \left({\frac {n}{2}}\right)}}\left[\Gamma \left({\frac {k+1}{2}}\right)\Gamma \left({\frac {n-k}{2}}\right)n^{\frac {k}{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aecd6a751df7ace0449d2eddecbfbf244c13405b)
![{\displaystyle \mathbb {E} [t]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54727cc7483a5fe221c117e0335061ac1a90b873)
![{\displaystyle \mathrm {D} [t]={n \over n-2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/952484d862cbb423bc5bed11fe1c6969ca26de01)























































































