Биномиальное распределение

Материал из Википедии — свободной энциклопедии

**Биномиальное распределение**
Функция вероятности
Функция распределения
Параметры	$n \geq 0$ — число «испытаний» $0\leq p \leq 1$ — вероятность «успеха»
Носитель	$k \in \{0,\dots,n\}\!$
Функция вероятности	$\binom{n}{k}\, p^k q^{n-k} \!$
Функция распределения	$I_{1-p}(n-\lfloor k\rfloor, 1+\lfloor k\rfloor) \!$
Математическое ожидание	$np\!$
Медиана	одно из $\{\lfloor np\rfloor-1, \lfloor np\rfloor, \lfloor np\rfloor+1\}$
Мода	$\lfloor (n+1)\,p\rfloor\!$
Дисперсия	$npq\!$
Коэффициент асимметрии	$\frac{1-2p}{\sqrt{npq}}\!$
Коэффициент эксцесса	$\frac{1-6pq}{npq}\!$
Информационная энтропия
Производящая функция моментов	$(q + pe^t)^n \!$
Характеристическая функция	$(q + pe^{it})^n \!$

Биномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из $n$ независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна $p$ .

[править] Определение

Пусть $X_1 ,\ldots, X_n$ — конечная последовательность независимых случайных величин с распределением Бернулли, то есть

$X_i = \left\{ \begin{matrix} 1, & p \\ 0, & q \equiv 1-p \end{matrix} \right.,\; i=1,\ldots, n.$

Построим случайную величину $Y$ :

$Y = \sum\limits_{i=1}^n X_i$ .

Тогда $Y$ , число единиц (успехов) в последовательности $X_1,\ldots, X_n$ , имеет биномиальное распределение с $n$ степенями свободы и вероятностью «успеха» $p$ . Пишем: $Y \sim \mathrm{Bin}(n,p)$ . Её функция плотности вероятности задаётся формулой:

$p_Y(k) \equiv \mathbb{P}(Y = k) = \binom{n}{k}\, p^k q^{n-k},\; k=0,\ldots, n,$

где $\binom{n}{k} = \frac{n!}{(n-k)! \, k!}$ — биномиальный коэффициент.

[править] Функция распределения

Функция распределения биномиального распределения может быть записана в виде суммы:

$F_Y(y) \equiv \mathbb{P}(Y \leq y) = \sum\limits_{k=0}^{\lfloor y \rfloor} \binom{n}{k}\, p^k q^{n-k},\; y \in\mathbb{R}$ ,

где $\lfloor y \rfloor$ обозначает наибольшее целое, не превосходящее число $y$ , или в виде неполной бета-функции:

$F_Y(k) \equiv \mathbb{P}(Y \le k ) = I_{1-p}(n-k,k+1)$ .

[править] Моменты

Производящая функция моментов биномиального распределения имеет вид:

$M_Y(t) = \left( pe^t + q\right)^n$ ,

откуда

$\mathbb{E}[Y] = np$ ,

$\mathbb{E}\left[Y^2\right] = np ( q + np )$ ,

а дисперсия случайной величины.

$\mathbb{D}[Y] = npq$ .

[править] Свойства биномиального распределения

Пусть $Y_1 \sim \mathrm{Bin}(n,p)$ и $Y 2 ˜Bin(n,1 - p)$ . Тогда $p_{Y_1}(k) = p_{Y_2}(n-k)$ .
Пусть $Y_1 \sim \mathrm{Bin}(n_1,p)$ и $Y_2 \sim \mathrm{Bin}(n_2,p)$ . Тогда $Y_1 + Y_2 \sim \mathrm{Bin}(n_1+n_2, p)$ .

[править] Связь с другими распределениями

Если $n = 1$ , то, очевидно, получаем распределение Бернулли.
Если $n$ большое, то в силу центральной предельной теоремы $\mathrm{Bin}(n,p) \approx N( np, npq )$ , где $N (n p, n p q)$ — нормальное распределение с математическим ожиданием $n p$ и дисперсией $n p q$ .
Если $n$ большое, а $λ$ — фиксированное число, то $\mathrm{Bin}(n, \lambda / n) \approx \mathrm{P}(\lambda)$ , где $P(λ)$ — распределение Пуассона с параметром $λ$ .

[править] См. также

	п·о·р Вероятностные распределения
	Одномерные	Многомерные
Дискретные:	Бернулли \| биномиальное \| геометрическое \| гипергеометрическое \| логарифмическое \| отрицательное биномиальное \| Пуассона \| равномерное	мультиномиальное
Абсолютно непрерывные:	Бета \| Вейбулла \| Гамма \| Колмогорова \| Коши \| Лапласа \| логнормальное \| Лоренца \| нормальное (Гаусса) \| Парето \| равномерное \| Стьюдента \| Фишера \| хи-квадрат \| экспоненциальное \| Эрланга	многомерное нормальное

Биномиальное распределение

Материал из Википедии — свободной энциклопедии

Содержание

[править] Определение

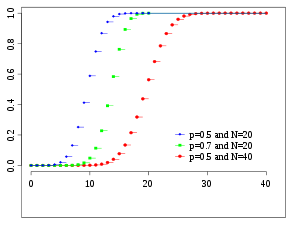[править] Функция распределения

[править] Моменты

[править] Свойства биномиального распределения

[править] Связь с другими распределениями

[править] См. также

Просмотры

Личные инструменты

Навигация

Поиск

Участие

Инструменты

На других языках