Разность множеств
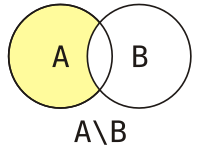
Ра́зность двух мно́жеств — теоретико-множественная операция, результатом которой является множество, в которое входят все элементы первого множества, не входящие во второе множество. Обычно разность множеств и обозначается как , но иногда можно встретить обозначение и .
Пусть и — два указанных в определении множества, тогда их разность определяется (на теоретико-множественном языке):
Когда , множество часто называют дополнением множества до множества .
Обычно предполагается, что рассматриваются подмножества одного и того же множества, которое, в этом случае называют универсумом, скажем, . Тогда можно рассматривать вместе с каждым множеством и его дополнение до множества — множество , при обозначении которого часто опускается значок универсума: [источник не указан 2832 дня]; при этом говорится, что — (просто) дополнение множества (без указания, дополнением до чего является данное множество).
С учётом данного замечания, оказывается, что , то есть дополнение множества до множества есть пересечение множества и дополнения множества .
Также применяется и операторная запись вида , или (если опустить универсальное множество) , , .
Операция разности множеств не является по определению симметричной по отношению ко входящим в неё множествам. Симметричный вариант теоретико-множественной разности двух множеств описывается понятием симметрической разности.
Примеры[править | править код]
- Пусть . Тогда
- Пусть — множество всех вещественных чисел, — множество рациональных чисел, а — множество целых чисел. Тогда — множество всех иррациональных чисел, а — дробных.
Свойства[править | править код]
Пусть — произвольные множества.
- Вычитание множества из самого себя даёт в результате пустое множество:
- Свойства пустого множества относительно разности:
- Разность двух множеств содержится в уменьшаемом:
- . Из этой формулы следует, что операция разности не является обратной операции суммы (то есть объединению).
- Разность не пересекается с вычитаемым:
- Разность множеств равна пустому множеству тогда и только тогда, когда уменьшаемое содержится в вычитаемом:
- Законы де Моргана в алгебре множеств формулируются следующим образом:
- , если .
- Если и , то
- Если , то для любого выполняется . Это соотношение имеет свой аналог в арифметике: если , то для любого справедливо .
Компьютерные реализации[править | править код]
В пакете Mathematica операция реализована с помощью функции Complement. В пакете MATLAB она же реализована с помощью функции setdiff.
В языке программирования Pascal (а также в его объектном расширении Object Pascal) операция разности множеств представлена оператором «−», обоими операндами и результатом выполнения которого являются значения типа set.
В языке программирования Python операция реализована с помощью метода diff над объектом типа set.
Дополнение множества[править | править код]
Определение[править | править код]
Если из контекста следует, что все рассматриваемые множества являются подмножествами некоторого фиксированного универсума , то определяется операция дополнения:
Свойства[править | править код]
- Операция дополнения является унарной операцией на булеане .
- Законы дополнения:[1]
- В частности, если оба и непусты, то является разбиением .
- Операция дополнения является инволюцией:
- Законы разности множеств:
Кодировка[править | править код]
| Графема | Название | Юникод | HTML | LaTeX |
|---|---|---|---|---|
| ∁ | COMPLEMENT | U+2201 | ∁
|
\complement
|
См. также[править | править код]
Литература[править | править код]
- Лавров И. А., Максимова Л. Л. Задачи по теории множеств, математической логике и теории алгоритмов. — М.: Физматлит, 2004. — 256 с.
- Куратовский К., Мостовский А. Теория множеств / Пер. с англ. М. И. Кратко, под ред. А. Д. Тайманова. — М.: Мир, 1970. — С. 16, 20—22.
Примечания[править | править код]
- ↑ Ильин В. А., Садовничий В. А., Сендов Бл. Х.. Глава 2. Вещественные числа // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 66. — 672 с. — ISBN 5-482-00445-7. Архивировано 23 июня 2015 года.






























































