Участник:Jumpow/Песочница: различия между версиями
Jumpow (обсуждение | вклад) Нет описания правки |
Jumpow (обсуждение | вклад) Нет описания правки |
||
| Строка 1: | Строка 1: | ||
[[Файл:30 St Mary Axe from Leadenhall Street.jpg|thumb|upright=1.3|«Корнишон»{{sfn|Freiberger|2007}}, [[Небоскрёб Мэри-Экс]], Лондон, completed 2003, с использованием {{не переведено 5|Параметрическое проектирование|параметрического проектирования||parametric design}} [[Тела вращения|solid of revolution]].]] |
|||
[[Файл:Samarkand Shah-i Zinda Tuman Aqa complex cropped2.jpg|thumb|upright=1.3|Орнамент гирих с инкрустированноым растительным украшением в ансамбле мавзолеев [[Шахи Зинда]] в [[Самарканд]]е, [[Узбекистан]]]] |
|||
[[Файл:Kandariya mahadeva temple.jpg|thumb|[[Кандарья-Махадева]], {{не переведено 5|Группа храмов Кхаджурахо|||Khajuraho}}, Индия, is an example of religious архитектуры with a [[Фрактал]]-like structure which has many parts that resemble the whole. c. 1030{{sfn|Rian, Park, Ahn, Chang|2007|с=4093–4107}}]] |
|||
'''Гирих''' ({{lang-fa|[[wikt:گره#Persian|گره]]}}, «узел»), а также {{lang|fa|گره سازی}} («завязывание узлов») — это вид [[Исламское искусство|исламского декоративного искусства]] в [[Архитектура|архитектуре]] и [[Народные художественные промыслы|художественных ремёслах]] (обложки книг, ковры, небольшие металлические объекты), состоящее из {{не переведено 5|Исламские геометрические орнаменты|геометрических линий||Islamic geometric patterns}}, образующих {{не переведено 5|Переплетение (искусство)|переплетённые||Interlace (art)}} {{не переведено 5|Переплетающийся орнамент|декоративные орнаменты||strapwork}}. В [[Персидская архитектура|персидской архитектуре]] орнаменты с узлами можно видеть в кирпичной кладке {{не переведено 5|банна’и|||banna'i}}, в изделиях из [[стукко]] и [[Мозаика|мозаичных]] [[фаянсовых]] работах{{sfn|Milwright|2001}}. Гирих определяется как «геометрические (часто в виде звёзд и многоугольников) рисунки, определяемые массивом точек, в которых (прямые) линии пересекаются»{{sfn|Allen|2004}}. |
|||
''Математика и архитектура''' are related, since, [[Математика и изобразительное искусство|as with other arts]], [[архитектор]]ы use [[Математика|математика]] for several reasons. Apart from the Математика needed when engineering [[Здание|здания]], архитекторы use [[Геометрия|геометрию]]: to define the spatial form of a building; from the [[Пифагореизм|Pythagoreans]] of the sixth century BC onwards, to create forms considered harmonious, and thus to lay out buildings and their surroundings according to mathematical, [[Эстетика|aesthetic]] and sometimes religious principles; to decorate buildings with mathematical objects such as [[Паркет (геометрия)|замощений]]; and to meet environmental goals, such as to minimise wind speeds around the bases of tall buildings. |
|||
В гирих используются симметричные узоры из прямолинейных отрезков. Гирих обычно состоит из переплетений, которые образуют 6-, 8-, 10- или 12-угольные звёзды, разделённые [[многоугольник]]ами и лентами, и часто они рисовались в {{не переведено 5|Переплетение (искусство)|переплетённом||Interlace (art)}} виде. Такие узоры обычно состоят из повторяющихся «единичных ячеек» с 2-, 3- или 6-кратной вращательной симметрией, которые [[Паркет (геометрия)|замощают]] плоскость без зазоров{{sfn|Lee|1987|с=182–197}}. |
|||
In [[Архитектура Древнего Египта|Древнем Египте]], [[Архитектура Древней Греции|Ancient Greece]], [[Индийская архитектура|Индии]], and the [[Исламская архитектура|Islamic world]], buildings including [[Египетские пирамиды|pyramids]], temples, мечети, palaces and [[Мавзолей|мавзолеи]] were laid out with specific proportions for religious reasons. В исламской архитектуре [[Геометрия|geometric]] shapes and {{не переведено 5|Исламские геометрические орнаменты|геометрические мозаичные орнаменты||Islamic geometric patterns}} are used to decorate buildings, both inside and outside. Some Hindu temples have a [[Фрактал]]-like structure where parts resemble the whole, conveying a message about the infinite in [[Индуистская космология|индуистской космологии]]. In [[Архитектура Китая|архитектуре Китая]], the [[тулоу]] of [[Фуцзянь|провинции Фуцзянь]] are circular, communal defensive structures. In the twenty-first century, mathematical ornamentation is again being used to cover public buildings. |
|||
Трёхмерный эквивалент гирих называется [[Сотовый свод|мукарны]]{{sfn|Rogers|1997|с=433–439}}. Он используется для украшения нижних частей [[купол]]ов или [[Тромп (архитектура)|тромпов]]. |
|||
In [[Архитектура Возрождения|Renaissance architecture]], [[Симметрия]] and proportion were deliberately emphasized by архитекторами such as [[Альберти, Леон Баттиста|Leon Battista Alberti]], [[Серлио, Себастьяно|Sebastiano Serlio]] and [[Палладио, Андреа|Andrea Palladio]], influenced by [[Витрувий|Vitruvius]]'s ''[[Десять книг об архитектуре|De architectura]]'' from [[Древний Рим|Ancient Rome]] и арифметика of the Pythagoreans from Ancient Greece. |
|||
==История== |
|||
At the end of the nineteenth century, [[Шухов, Владимир Григорьевич|Vladimir Shukhov]] in [[Russia]] and [[Гауди, Антонио|Antoni Gaudí]] in [[Барселона]] pioneered the use of [[Гиперболоидные конструкции]]; in the [[Саграда-Фамилия]], Gaudí also incorporated [[Гипербола (математика)|hyperbolic]] [[Параболоид]]s, tessellations, {{не переведено 5|Арка с очертанием обратной цепной линии|||catenary arch}}es, [[Катеноид]]s, [[Геликоид]]s, and [[Линейчатая поверхность|ruled surface]]s. In the twentieth century, styles such as [[Архитектурный модернизм]] and [[Деконструктивизм]] explored different geometries to achieve desired effects. [[Минимальная поверхность|Minimal surface]]s have been exploited in tent-like roof coverings as at [[Денвер (аэропорт)|Denver International Airport]], while [[Фуллер, Ричард Бакминстер|Richard Buckminster Fuller]] pioneered the use of the strong [[Перекрытие-оболочка|thin-shell structure]]s known as [[Геодезический купол|geodesic dome]]s. |
|||
{{Подробно|Исламские геометрические орнаменты}} |
|||
==Connected fields== |
|||
===Корни=== |
|||
[[Файл:CdM, presunto autoritratto di leon battista alberti, white ground.jpg|thumb|upright|In the [[Возрождение]], [[архитектор]] like [[Альберти, Леон Баттиста|Leon Battista Alberti]] was expected to be knowledgeable in many disciplines, including [[Арифметика|арифметику]] и [[Геометрия|геометрию]].]] |
|||
Считается, что орнаменты в стиле гирих были навеяны узловыми орнаментами [[Сирия (римская провинция)|сирийской провинции Римской Империи]], которые датируются вторым столетием нашей эры {{sfn|Milwright|2001}}. Предшественниками гирих были криволинейные переплетённые орнаменты с трёхкратной вращательной симметрией. [[Мечеть Омейядов]] (709–715) в Дамаске, Сирия, имеет оконные решётки, имеющие волнообразный переплетённый орнамент в виде шестиугольных звёзд {{sfn|Broug|2008|с=153}}. Ранние примеры {{не переведено 5|Исламские геометрические орнаменты|исламских геометрических орнаментов||Islamic geometric patterns}} сделанные из прямых лент можно видеть в архитектуре сохранившихся к настоящему времени воротах караван-сарая в [[Рабат Малик]], Узбекистан (1078){{sfn|Broug|2008|с=71}}. |
|||
Архитекторы Michael Ostwald and Kim Williams, considering the relationships between [[Архитектура|архитектурой]] и [[Математика|математикой]], note that the fields as commonly understood might seem to be only weakly connected, since Архитектура is a profession concerned with the practical matter of making buildings, while Математика is the pure [[Теория чисел|study of number]] and other abstract objects. But, they argue, the two are strongly connected, and have been since [[Античность|antiquity]]. In Древнем Риме, [[Витрувий]] described an архитектору as a man who knew enough of a range of other disciplines, primarily [[Геометрия]], to enable him to oversee skilled artisans in all the other necessary areas, such as masons and carpenters. The same applied in the [[Средние века]], where graduates learnt [[Арифметика|арифметику]], геометрию and [[Эстетика|эстетику]] alongside the basic syllabus of grammar, logic, and rhetoric ([[тривиум]]) in elegant halls made by master builders who had guided many craftsmen. A master builder at the top of his profession was given the title of архитектора or engineer. In the [[Возрождение|Возрождения]], [[квадривиум]] of арифметика, геометрия, music and astronomy became an extra syllabus expected of the [[Универсальный человек|человек эпохи Возрождения]] such as [[Альберти, Леон Баттиста|Leon Battista Alberti]]. Similarly in England, Sir [[Рен, Кристофер|Christopher Wren]], known today as архитектор, was firstly a noted astronomer{{sfn|Williams, Ostwald|2015|с=chapter 1. 1–24}}. |
|||
<gallery mode=nolines> |
|||
File:Bosra mosaic.jpg|Римская мозаика 2-го века в [[Босра|Босре]] с криволинейными орнаментальными узлами |
|||
Williams and Ostwald, further overviewing the interaction of математики and Архитектура since 1500 according to the approach of the German sociologist [[Адорно, Теодор|Theodor W. Adorno|Theodor Adorno]], identify three tendencies among архитекторов, namely: to be [[Революция|revolutionary]], introducing wholly new ideas; [[Политическая реакция|реакционеры]], failing to introduce change; or {{не переведено 5|Художники возрождения|||revivalist artist}}, actually going backwards. They argue that архитекторы have avoided looking to Математика for inspiration in revivalist times. This would explain why in revivalist periods, such as the [[Неоготика]] in 19th century England, Архитектура had little connection to математикой. Equally, they note that in reactionary times such as the Italian [[Маньеризм]] of about 1520 to 1580, or the 17th century [[барокко]] and [[Палладианство]] movements, Математика was barely consulted. In contrast, революционные early 20th century movements such as [[футуризм]] and {{не переведено 5|Архитектура конструктивизма|конструктивизм||Constructivist architecture}} actively rejected old ideas, embracing Математика and leading to [[Модернизм]] Архитектура. Towards the end of the 20th century, too, [[Фрактал|fractal]] геометрияwas quickly seized upon by архитекторами, as was {{не переведено 5|Непериодичное замощение|||aperiodic tiling}}, to provide interesting and attractive coverings for buildings{{sfn|Williams, Ostwald|2015|с=1-24, chapter 48}}. |
|||
File:Hishams Palace window Author MDarter.jpg|Криволинейное переплетение 8-ого века в окне замка {{не переведено 5|Дворец Хишама|Хирбет Аль-Мафджар||Hisham's Palace}}, [[Иерихон]] |
|||
Архитекторы используют математику for several reasons, leaving aside the necessary use of математики in the {{не переведено 5|Архитектурное проектирование|проектировании зданий||Architectural engineering}}{{sfn|Overview}}. Firstly, they use геометрию because it defines the spatial form of a building{{sfn|Leyton|2001}}. Secondly, they use математику to design forms that are [[Эстетика|considered beautiful]] or harmonious{{sfn|Stakhov, Olsen|2009}}. From the time of the [[Пифагореизм|Pythagoreans]] with their religious philosophy of number{{sfn|Smith|1870|с=620}}, архитекторы in [[Архитектура Древней Греции|Ancient Greece]], [[Древний Рим]], the [[Исламская архитектура|Islamic world]] and the [[Архитектура Возрождения|Italian Renaissance]] have chosen the [[Пропорция (архитектура)|proportion]]s of the built environment – buildings and their designed surroundings – according to mathematical as well as эстетика and sometimes religious principles{{sfn|Vitruvius|2009|с=8–9}}{{sfn|Tennant|2003}}{{sfn|Rai|1993|с=19–48}}{{sfn|O'Connor , Robertson|2002}}. Thirdly, they may use mathematical objects such as [[Паркет (геометрия)|tessellation]]s to decorate buildings{{sfn|van den Hoeven, van der Veen|2010}}{{sfn|Cucker|2013|с=103–106}}. Fourthly, they may use математику in the form of computer modelling to meet environmental goals, such as to minimise whirling air currents at the base of tall buildings{{sfn|Freiberger|2007}}. |
|||
==Harmonious spatial forms== |
|||
===Secular эстетика=== |
|||
====Древний Рим==== |
|||
[[Файл:Greekhse1.jpg|thumb|upright=1.3|Plan of a Greek house by [[Витрувий|Vitruvius]]]] |
|||
=====Витрувий===== |
|||
{{Подробно|Витрувий|Виртувианов модуль|Десять книг об архитектуре}} |
|||
[[Файл:Pantheon-panini.jpg|thumb|left|upright|The interior of the [[Пантеон (Рим)|Pantheon]] by [[Панини, Джованни Паоло|Джованни Паоло Панини]], 1758]] |
|||
The influential Ancient Roman архитектор Витрувий argued that the design of a building such as a temple depends on two qualities, proportion and ''symmetria''. Proportion ensures that each part of a building relates harmoniously to every other part. ''Symmetria'' in Витрувий's usage means something closer to the English term modularity than [[Зеркальная симметрия|mirror symmetry]], as again it relates to the assembling of (modular) parts into the whole building. In his базилике at [[Фано (город)|Fano]], he uses ratios of small integers, especially the [[Треугольное число|triangular number]]s (1, 3, 6, 10, ...) to proportion the structure into {{не переведено 5|Виртувианов модуль|(виртувиановы) модули||Vitruvian module}}.{{efn|In Book 4, chapter 3 of ''[[Десять книг об архитектуре|De architectura]]'', he discusses modules directly{{sfn|Vitruvius}}}} Thus Базилика's width to length is 1:2; the aisle around it is as high as it is wide, 1:1; the columns are five feet thick and fifty feet high, 1:10{{sfn|Vitruvius|2009|с=8–9}}. |
|||
[[Файл:Dehio 1 Pantheon Floor plan.jpg|thumb|upright|Floor plan of the Pantheon]] |
|||
Витрувий named three qualities required of Архитектура in his ''[[Десять книг об архитектуре|De architectura]]'', c. 15 B.C.: firmness, usefulness (or «Commodity» in [[Уоттон, Генри|Henry Wotton]]'s 16th century English), and delight. These can be used as categories for classifying the ways in which математика is used in архитектуре. Firmness encompasses the use of математики to ensure a building stands up, hence the mathematical tools used in design and to support construction, for instance to ensure stability and to model performance. Usefulness derives in part from the effective application of математики, reasoning about and analysing the spatial and other relationships in a design. Delight is an attribute of the resulting building, resulting from the embodying of mathematical relationships in the building; it includes эстетику, sensual and intellectual qualities{{sfn|Williams, Ostwald|2015|с=42, 48}}. |
|||
=====The Pantheon===== |
|||
{{Основная статья|Пантеон (Рим)}} |
|||
[[Пантеон (Рим)|Пантеон]] в Риме has survived intact, illustrating classical Roman structure, proportion, and decoration. The main structure is a dome, the apex left open as a circular [[Окулюс|oculus]] to let in light; it is fronted by a short colonnade with a triangular pediment. The height to the окулюс and the diameter of the interior circle are the same, {{convert|43.3|m|ft}}, so the whole interior would fit exactly within a cube, and the interior could house a sphere of the same diameter{{sfn|Roth|1992|с=36}}. These dimensions make more sense when expressed in [[Список древнеримских единиц|списке древнеримских единиц]]: The dome spans 150 {{не переведено 5|Римский фут|римских футов||Roman foot}}{{efn|{{не переведено 5|Римский фут|||Roman foot}} was about {{convert|0.296|m|ft}}.}}); Окулюс is 30 Roman feet in diameter; the doorway is 40 Roman feet high{{sfn|Claridge|1998|с=204–5}}. The Pantheon remains the world's largest unreinforced concrete dome{{sfn|Lancaster|2005|с=44–46}}. |
|||
====Возрождение==== |
|||
{{Подробно|Архитектура Возрождения}} |
|||
[[Файл:Santa Maria Novella.jpg|thumb|Facade of [[Санта-Мария-Новелла]], [[Флоренция]], 1470. The frieze (with squares) and above is by [[Альберти, Леон Баттиста|Leon Battista Alberti]].]] |
|||
Первым трактатом эпохи возрождения по архитектуре был трактат Леона Баттиста Альберти (1450) {{не переведено 5|On the Art of Building|''On the Art of Building''||De re aedificatoria}} (Об искусстве строительства). Трактат стал первой печатной книгой по архитектуре в 1485. Трактат частично базировался на книге Витрувия ''Десять книг об архитектуре'' и, через [[Никомах Герасский|Никомах]], пифагоровой арифметике. Альберти начинает с куба и выводит из него пропорции. Так, диагонали грани дают отношение 1:√2, а диаметр сферы, описаннвй вокруг куба имеет отношение 1:√3{{sfn|March|1996|с=54–65 }}{{sfn|Mathalino.com}}. Альберто также описывает открытие [[Брунеллески, Филиппо|Филиппо Брунеллески]] {{не переведено 5|Перспектива (графика)|линейной перспективы||perspective (graphical)}}, разработанной для планирования зданий, которые выглядят вполне пропорционально, если рассматривать с удобного расстояния{{sfn|O'Connor , Robertson|2002}}. |
|||
[[Файл:Houghton Typ 525.69.781 - Serlio, 69.jpg|thumb|left|Архитекторная перспектива of a stage set by [[Серлио, Себастьяно|Sebastiano Serlio]], 1569<ref>Typ 525.69.781, Houghton Library, Harvard University</ref>]] |
|||
Следующим важным текстом была книга [[Серлио, Себастьяно|Себастьяна Серлио]] ''Regole generali d'architettura'' (''Основные правила архитектуры''). Первый том книги вышел в Венеции в 1537. Том 1545-го года (книги 1 и 2) охватывают геометрию и {{не переведено 5|Перспектива (графика)|перспективу||perspective (graphical)}}. Два метода Серлио построения перспективы были ошибочными, но это не остановило широкое использование книги{{sfn|Andersen|2008|с=117–121}}. |
|||
[[Файл:Villa Pisani.jpg|thumb|right|[[ Палладио, Андреа|Andrea Palladio]]'s plan and elevation of the {{не переведено 5|Вилла Пизани (Баньоло)|Вилла Пизани||Villa Pisani (Bagnolo)}}]] |
|||
В 1570 [[Палладио, Андреа|Андреа Палладио]] опубликовал авторитетные ''[[Четыре книги об архитектуре|I quattro libri dell'architettura]]'' (Четыре книги об архитектуре) в [[Венеция|Венеции]]. Эти книги получили широкое распространение и распространяли идеи итальянского возрождения на остальную Европу в содействии со сторонниками идей, такими как английский дипломат Генри Уоттон, выпустивший в 1624 ''Элементы архитектуры''{{sfn|Ruhl}}. Пропорции каждого помещения внутри особняка вычислялись с помощью простых математических отношений, таких как 3:4 и 4:5, и различные помещения внутри дома были связаны этими соотношениями. Ранние архитекторы использовали эти формулы для балансирования симметрии фасада. Однако, проекты Палладио относились, как правило, к квадратным особнякам{{sfn|Copplestone|1963|с=251}}. Палладио допускал ряд отношений в ''Quattro libri'', утверждая{{sfn|Wassell}}{{sfn|Palladio|1997|с=book I, chapter xxi, page 57}}: |
|||
{{quote|Имеется семь типов помещений, наиболее прекрасных и хорошо пропорциональных. Это круглые, хотя они редки, квадратные или их длина равна диагонали квадрата ширины, ширине с третью, ширине с половиной, ширине и две трети и две ширины.{{efn|In modern algebraic notation, these ratios are respectively 1:1, √2:1, 4:3, 3:2, 5:3, 2:1.}}}} |
|||
In 1615, [[Скамоцци, Винченцо|Vincenzo Scamozzi]] published the late Возрождение treatise ''L'Idea dell'Architettura Universale'' (The Idea of a Universal Архитектуры){{sfn|Scamozzi|2003}}. He attempted to relate the design of cities and buildings to the ideas Витрувия and the Pythagoreans, and to the more recent ideas of Palladio{{sfn|Borys|2014|с=140–148 and passim}}. |
|||
====Девятнадцатый век==== |
|||
[[Файл:Adziogol hyperboloid Lighthouse by Vladimir Shukhov 1911.jpg|thumb|upright=0.5|[[ Гиперболоидные конструкции|Hyperboloid lattice]] [[Аджигольский маяк|маяк]] by [[Шухов, Владимир Григорьевич|Vladimir Shukhov]], [[Украина]], 1911]] |
|||
[[Гиперболоидные конструкции]] were used starting towards the end of the nineteenth century by [[Шухов, Владимир Григорьевич|Vladimir Shukhov]] for masts, lighthouses and cooling towers. Their striking shape is both эстетический interesting and strong, using structural materials economically. [[Шуховская башня (Полибино)|Shukhov's first hyperboloidal tower]] was exhibited in [[Нижний Новгород|Нижнем Новгороде]] в 1896{{sfn|Beckh|2015|с=75 and passim}}{{sfn|The Engineer|1897|с=292–294}}{{sfn|Graefe|1990|с=110–114}}. |
|||
====Двадцатый век==== |
|||
{{Подробно|Архитектурный модернизм|Aрхитектура 21-го века}} |
|||
[[Файл:Rietveld Schröderhuis HayKranen-7.JPG|thumb|left|[[Де Стейл]]'s sliding, intersecting planes: [[Дом Шрёдер]], 1924]] |
|||
The early twentieth century movement [[Архитектурный модернизм|Modern Architecture]], pioneered{{efn|Constructivism influenced Bauhaus and Ле Корбюзье, for example{{sfn|Hatherley|2011}} by Russian [[Конструктивизм (искусство)|Constructivism]]{{sfn|Hatherley|2011}}, used rectilinear [[Евклидова геометрия|Euclidean]] (also called [[Прямоугольная система координат|декартовыми]]) Геометрия. In the [[Де Стейл]] movement, the horizontal and the vertical were seen as constituting the universal. Архитектурные form consists of putting these two directional tendencies together, using roof planes, wall planes and balconies, which either slide past or intersect each other, as in the 1924 [[Дом Шрёдер]] by [[Ритвельд, Геррит|Gerrit Rietveld]]{{sfn|Rietveld Schröderhuis}}. |
|||
[[Файл:Raoul Heinrich Francé Poppy and Pepperpot from Die Pflanze als erfinder 1920.jpeg|thumb|{{не переведено 5|Франсе, Рауль Генрих|Рауля Генриха Франсе||Raoul Heinrich Francé}} [[мак]] и [[Солонка|перечница]] ([[Бионика|biomimetics]]) image from ''Die Pflanze als Erfinder'', 1920]] |
|||
Архитекторы модернизма were free to make use of curves as well as planes. [[Холден, Чарльз|Charles Holden]]'s 1933 {{не переведено 5|станция лондонской подземки в Арнос Гроув|||Arnos Grove tube station}} has a circular ticket hall in brick with a flat concrete roof.<ref>{{NHLE|num=1358981|desc=|accessdate=5 October 2015}}</ref> In 1938, the [[Баухаус|Bauhaus]] painter [[Мохой-Надь, Ласло|Laszlo Moholy-Nagy]] adopted {{не переведено 5|Франсе, Рауль Генрих|Рауля Генриха Франсе||Raoul Heinrich Francé}} seven [[Бионика|biotechnical]] elements, namely the crystal, the sphere, the cone, the plane, the (cuboidal) strip, the (cylindrical) rod, and the spiral, as the supposed basic building blocks of Архитекторы inspired by nature{{sfn|Moholy-Nagy|1938|с=46}}{{sfn|Gamwell|2015|с=306}}. |
|||
[[Ле Корбюзье|Le Corbusier]] proposed an [[Антропометрия|anthropometric]] масштаб of proportions in архитектуре, [[модулор]] (система пропорций), based on the supposed height of a man{{sfn|Le Corbusier|2004}}. Ле Корбюзье's 1955 [[Нотр-Дам-дю-О]] uses free-form curves not describable in mathematical formulae.{{efn|Pace Nikos Salingaros, who suggests the contrary{{sfn|Salingaros}}, but it is not clear exactly what Математика may be embodied in the curves of Ле Корбюзье's chapel.{{sfn|Greene}}}} The shapes are said to be evocative of natural forms such as the {{не переведено 5|Нос корабля|нос||prow}} корабля or praying hands{{sfn|Hanser|2006|с=211}}. The design is only at the largest scale: there is no hierarchy of detail at smaller scales, and thus no Фрактал dimension; the same applies to other famous twentieth-century buildings such as the [[Сиднейский оперный театр]], [[Денвер (аэропорт)|Denver International Airport]], and the [[Музей Гуггенхейма в Бильбао]] {{sfn|Salingaros}}. |
|||
{{не переведено 5|Aрхитектура 21-го века|||Contemporary architecture}}, in the opinion of the 90 leading архитекторыwho responded to a 2010 {{не переведено 5|Опрос о мировой архитектуре|||World Architecture Survey}}, is extremely diverse; the best was judged to be Фрэнк Гери's Музей Гуггенхейма в Бильбао{{sfn|World Architecture Survey|2010}}. |
|||
[[Файл:DIA Airport Roof.jpg|thumb|left|upright=2.5|[[Минимальная поверхность|Минимальные поверхности]] of the {{не переведено 5|Тканевая структура|тканевой крыши||fabric structure}} of [[Денвер (аэропорт)|Denver International Airport]], completed in 1995, evoke [[Колорадо|Colorado]]'s snow-capped mountains and the [[Типи|teepee]] tents of [[Коренные народы США|Native American]]s.]] |
|||
Здание терминала Международного аэропорта Дэнвера, построенные в 1995, has a {{не переведено 5|Тканевая структура|тканевую крышу||fabric structure}} supported as a [[Минимальная поверхность]] (i.e., its {{не переведено 5|средняя кривизна|||mean curvature}} is zero) by steel cables. It evokes [[Колорадо|Colorado]]'s snow-capped mountains and the [[Типи|teepee]] tents of [[Коренные народы США|Native American]]s (часто их неверно называют вигвамами){{sfn|Denver Airport Press Kit}}{{sfn|Denver International Airport}}. |
|||
Архитектор [[Фуллер, Ричард Бакминстер|Richard Buckminster Fuller]] is famous for designing strong [[Перекрытие-оболочка|thin-shell structure]]s known as [[Геодезический купол|geodesic dome]]s. [[Биосфера (Монреаль)]] dome is {{convert|61|m|ft}} high; its diameter is {{convert|76|m|ft}}{{sfn|Biosphere}}. |
|||
Сиднейский оперный театр has a dramatic roof consisting of soaring white vaults, reminiscent of ship's sails; to make them possible to construct using standardized components, the vaults are all composed of triangular sections of spherical shells with the same radius. These have the required uniform [[Кривизна|curvature]] in every direction{{sfn|Hahn|2013}}. |
|||
The late twentieth century movement ''[[Деконструктивизм]]'' creates deliberate disorder with what [[Салингарос, Никос|Nikos Salingaros]] в книге ''[[A Theory of Architecture]]'' (''Теория архитектуры'') calls random forms{{sfn|Salingaros|2006|с=139–141}} of high complexity{{sfn|Salingaros|2006|с=124–125}} by using non-parallel walls, superimposed grids and complex 2-D surfaces, as in [[Фрэнк Гери|Frank Gehry]]'s [[Концертный зал имени Уолта Диснея]] and Музей Гуггенхейма в Бильбао{{sfn|Gehry, Mudford, Koshalek|2009}}{{sfn|Garcetti|2004}}. Until the twentieth century, Архитектура students were obliged to have a grounding in математике. Salingaros argues that first «overly simplistic, politically-driven» [[Модернизм]] and then «anti-scientific» Деконструктивизм have effectively separated Архитектура from математики. He believes that this «reversal of mathematical values» is harmful, as the «pervasive aesthetic» of non-mathematical Архитектура trains people «to reject mathematical information in the built environment»; he argues that this has negative effects on society{{sfn|Salingaros}}. |
|||
<gallery> |
|||
File:Bauhaus-Dessau Wohnheim Balkone.jpg|{{не переведено 5|Новая Вещественность (архитектура)|Новая Вещественность||New Objectivity (architecture)}}: [[Гропиус, Вальтер|Walter Gropius]]'s [[Баухаус|Bauhaus]], [[Дессау]], 1925 |
|||
File:Arnos Grove underground station 16 November 2012.jpg|[[Цилиндр]]: [[Холден, Чарльз|Charles Holden]]'s {{не переведено 5|станция лондонской подземки в Арнос Гроув|||Arnos Grove tube station}}, 1933 |
|||
File:RonchampCorbu.jpg|[[Архитектурный модернизм|Модернизм]]: [[Ле Корбюзье|Le Corbusier]]'s [[Нотр-Дам-дю-О]], 1955 |
|||
File:Mtl. Biosphere in Sept. 2004.jpg|[[Геодезический купол]]: [[Биосфера (Монреаль)]] by [[Фуллер, Ричард Бакминстер|R. Buckminster Fuller]], 1967 |
|||
File:Sydney Opera House Sails.jpg|Uniform [[Кривизна]]: [[Сиднейский оперный театр]], 1973 |
|||
File:Image-Disney Concert Hall by Carol Highsmith edit-2.jpg|[[Деконструктивизм]]: [[Концертный зал имени Уолта Диснея]], Los Angeles, 2003 |
|||
</gallery> |
</gallery> |
||
===Religious principles=== |
|||
[[Файл:Al-Bawwab Koran girih.JPG|thumb|upright|Украшение [[Коран]]а (1000–1001 нашей эры) made by {{не переведено 5|Ибн аль-Бавваб|||Ibn al-Bawwab}}]] |
|||
====Древний Египет==== |
|||
===Украшение рукописей=== |
|||
{{Подробно|Древнеегипетские погребальные обряды}} |
|||
Ранние формы гирих в книгах есть на обложке [[Коран]]а примерно 1000-го года, найденного в [[Багдад]]е{{sfn|Wade|2006}}. Этот Коран имеет украшенные рисунками страницы со сплетёнными восьмиугольниками и записанную каллиграфией [[сулюс]]{{sfn|Tabbaa|2002|с=84}}. |
|||
[[Файл:All Gizah Pyramids.jpg|thumb|left|[[Древний Египет|древнеегипетские]] [[Пирамида (архитектура)|pyramid]]s at Giza have mathematical proportions, either by accident or by design.]] |
|||
===Работа по дереву=== |
|||
[[Файл:Mathematical Pyramid.svg|thumb|Base:hypotenuse (b:a) ratios for pyramids like the [[Пирамида Хеопса]] could be: 1:φ ([[треугольник Кеплера]]), 3:5 ({{не переведено 5|Специальные прямоугольные треугольники|треугольник 3-4-5||3-4-5 triangle}}), or 1:4/π]] |
|||
[[Файл:Cairo, moschea di ibn tulun, minbar 05.JPG|thumb|upright|[[Минбар]] 13-го века, [[Мечеть Ибн Тулуна]], Каир]] |
|||
Одно из наиболее ранних сохранившихся примеров исламского геометрического искусства, это деревянный [[минбар]] 13-го века [[Мечеть Ибн Тулуна|мечети Ибн Тулуна]] в Каире{{sfn|Lekegian}}{{sfn|Broug|2008|с=66–69}}. |
|||
The [[Пирамида (архитектура)|pyramid]]s of [[Древний Египет|Древнего Египта]] are [[Древнеегипетские погребальные обряды|tombs]] constructed with deliberately chosen proportions, but which these were has been debated. The face angle is about 51°85’, and the ratio of the slant height to half the base length is 1.619, less than 1% from the [[Золотое сечение|золотого сечения]]. If this was the design method, it would imply the use of [[Треугольник Кеплера|треугольника Кеплера]] (face angle 51°49’){{sfn|Markowsky|1992}}{{sfn|Taseos|1990}}. However it is more likely that the pyramids' slope was chosen from the {{не переведено 5|Специальные правильные треугольники|тругольник 3-4-5||Special right triangles}} (face angle 53°8’), known from the [[Папирус Ахмеса|папируса Ахмеса]] (c. 1650 – 1550 BC); or from the triangle with base to hypotenuse ratio 1:4/π (face angle 51°50’){{sfn|Gazale|1999}}. |
|||
The possible use of the 3-4-5 triangle to lay out right angles, such as for the ground plan of a pyramid, and the knowledge of Pythagoras theorem which that would imply, has been much asserted{{sfn|Cooke|2011|с=237–238}}. It was first conjectured by the historian [[Кантор, Мориц Бенедикт|Moritz Cantor]] in 1882{{sfn|Cooke|2011|с=237–238}}. It is known that right angles were laid out accurately in древнем Египте{{sfn|Cooke|2011|с=237–238}}; that their surveyors did use {{не переведено 5|Верёвка с узлами|верёвку с узлами||knotted cord}}s for measurement{{sfn|Cooke|2011|с=237–238}}; that [[Плутарх]] recorded in ''[[Моралии (Плутарх)|Об Исиде и Осирисе]]'' (around 100 AD) that the Egyptians admired the 3-4-5 triangle{{sfn|Cooke|2011|с=237–238}}; and that the {{не переведено 5|Берлинский папирус 6619|||Berlin Papyrus 6619}} from the [[Среднее царство|Среднего царства]] (before 1700 BC) stated that «the area of a square of 100 is equal to that of two smaller squares. The side of one is ½ + ¼ the side of the other.»{{sfn|Gillings|1982|с=161}}. The historian of математики Roger L. Cooke observes that «It is hard to imagine anyone being interested in such conditions without knowing the Теорема Пифагора.» {{sfn|Cooke|2011|с=237–238}} Against this, Cooke notes that no Egyptian text before 300 BC actually mentions the use of the theorem to find the length of a triangle's sides, and that there are simpler ways to construct a right angle. Cooke concludes that Cantor's conjecture remains uncertain: he guesses that the древний египтяне probably did know the Теорема Пифагора, but that «there is no evidence that they used it to construct right angles»{{sfn|Cooke|2011|с=237–238}}. |
|||
В деревянных изделиях узоры гирих могут быть созданы двумя различными методами. В одном методе сначала создаётся деревянная решётка с геометрическими фигурами (многоугольники или звёзды), затем отверстия могут быть заполнены каким-либо материалом, либо не заполняться. В другом методе, называемом ''гирих-чини''{{sfn|Henry|2007}}, деревянные панели с геометрическими фигурами создаются отдельно, затем они комбинируются для создания сложного орнамента{{sfn|Milwright|2001}}. Эта техника работы с деревом была популярна в период [[Сефевиды|сефевидов]]. Примеры этой техники наблюдаются в различных исторических структурах [[Исфахан]]а. |
|||
====Древняя Индия==== |
|||
===Архитектура=== |
|||
{{Подробно|Индийская архитектура|Васту-шастра}} |
|||
[[Файл:Kayseri-Huant-Hatun-Mosque2-Verity-Cridland.jpg|thumb|left|150px|Орнаменты Гириха на стенах, окружающих ворота медресе Хунат Хатун (архитектура периода Сельджуков – примерно 1178–1243) в Кайсери, Турция.]] |
|||
Термин «гирих» обозначал в турецком языке многоугольный ленточный узор, используемый в архитектуре начиная с конца 15-го века{{sfn|Dündar|2003|с=131–172}}. В конце 15-го века узоры гирих были приведены художниками в каталогах узоров, таких как {{не переведено 5|свиток Топкапы|||Topkapı Scroll}}{{sfn|Katz|2007|с=620}}. |
|||
[[Файл:Virupaksha Temple,Hampi.JPG|thumb|upright|left|[[Гопурам]] [[Индус|индусского]] [[Храм Вирупакши в Хампи|храма Вирупакши]] в [[Хампи]] has a [[Фрактал]]-like structure where the parts resemble the whole.]] |
|||
Хотя криволинейные узоры гирих встречались в 10-м веке, Полностью разработанные орнаменты гирих не попадались до 11-го века. Орнамент стал доминирующим элементом в 11-м и 12-м веках, например, в резных панелях [[стукко]] с переплетённым орнаментом гирих, который можно видеть на {{не переведено 5|Башни Харракана|башнях Харракана||Kharraqan towers}} (1067) возле [[Казвин (остан)|Казвина, Иран]] {{sfn|Milwright|2001}}{{sfn|Pugachenkova|1986}}. Украшение в виде стилизованного растения было иногда согласовано с гирих{{sfn|Pugachenkova, Dani, Yingsheng|2000}}. |
|||
[[Васту-шастра|Vaastu Shastra]], the ancient [[Индия|India]]n canons of архитектуры and town planning, employs symmetrical drawings called [[Мандала|мандалы]]. Complex calculations are used to arrive at the dimensions of a building and its components. The designs are intended to integrate Архитектура with nature, the relative functions of various parts of the structure, and ancient beliefs utilizing geometric patterns ([[Янтры|yantra]]), Симметрия and {{не переведено 5|Относительное направление|направление||Direction (geometry, geography)}} alignments{{sfn|Kramrisch|1976}}{{sfn|Sachdev, Tillotson|2004|с=155–160}. However, early builders may have come upon mathematical proportions by accident. The mathematician Georges Ifrah notes that simple «tricks» with string and stakes can be used to lay out geometric shapes, such as ellipses and right angles{{sfn|O'Connor , Robertson|2002}}{{sfn|Ifrah|998}}. |
|||
После периода [[Сефевиды|сефевидов]] использование гирих продолжалось в период династии [[Сельджукиды|cельджукидов]] и в поздний период [[Государство Хулагуидов|хулагидов]]. В 14-ом веке гирих становится незначительным элементом в декоративном искусстве и был вытеснен растительными узорами во время эры [[Тимуриды|тимуридов]]. Однако, геометрические ленточные узоры продолжали быть важным элементом декоративного искусства в монументах Центральной Азии и после периода тимуридов {{sfn|Milwright|2001}}. |
|||
{{clear}} |
|||
[[Файл:Plan of Meenakshi Amman Temple Madurai India.jpg|thumb|upright|Plan of [[Храм Минакши]], [[Мадурай]], from 7th century onwards. The four gateways (numbered I-IV) are tall [[Гопурам|gopuram]]s.]] |
|||
==Построение== |
|||
{{Кратное изображение|зона=right|изобр1=Girih compass straightedge example.svg|ширина1=300|изобр2=Window Apartments of the Crown Prince.JPG|ширина2=150|подпись1=Орнамент гирих, который можно построить с помощью [[Построение с помощью циркуля и линейки|циркуля и линейки]]|подпись2=Решётка на окне в [[Топкапы|Дворце Топкапы]], созданная с этим узором гирих.}} |
|||
Математика [[фрактал]]ов has been used to show that the reason why existing buildings have universal appeal and are visually satisfying is because they provide the viewer with a sense of scale at different viewing distances. For example, in the tall [[Гопурам|gopuram]] gatehouses of [[Индус|Hindu]] temples such as the [[Храм Вирупакши в Хампи|Virupaksha Temple]] at [[Хампи|Hampi]] built in the seventh century, and others such as the [[Кандарья-Махадева|храм Кандарья-Махадева]] at {{не переведено 5|Группа храмов Кхаджурахо|||Khajuraho}}, the parts and the whole have the same character, with [[Фрактальная размерность|фрактальной размерностью]] in the range 1.7 to 1.8. The cluster of smaller towers (''shikhara'', lit. 'mountain') about the tallest, central, tower which represents the holy [[Кайлас|гора Кайлас]], abode of божества [[Шива]], depicts the endless repetition of universes in [[Индуистская космология|индуистской космологии]] {{sfn|Rian, Park, Ahn, Chang|2007|с=4093–4107}}{{sfn|Fractals in Indian Architecture}} The religious studies scholar William J. Jackson observed of the pattern of towers grouped among smaller towers, themselves grouped among still smaller towers, that: |
|||
Первые узоры гирих были сделаны путём копирования орнамента по правильной [[Решётка (теория графов)|решётке]]. Узор рисовался с помощью [[Циркуль|циркуля]] и [[Линейка|линейки]]. Современные художники для создания традиционной техники используют пару [[Штангенинструмент|делителей]] (центрировочных циркулей), чтобы сделать насечки на бумажном листе, который затем оставляется на солнце, чтобы он стал ломким. Прямые линии рисуются карандашом и немаркированной линейкой <ref>Эрик Бруг в книге «''Islamic Geometric Patterns''» (''Исламские геометрические узоры'') иллюстрирует много таких узоров, и в приложении даёт детальную инструкцию по их построению с помощью циркуля илинейки {{harv|Broug|2008|с=194–243}}</ref>{{sfn|Henry|2007}}. Орнаменты гирих, сделанные таким образом подобны [[Паркет (геометрия)|двумерному кристаллу]], замощающему пространство с помощью единичной ячейки. Поскольку замощение сделано с помощью операций [[Параллельный перенос|параллельного переноса]] или [[Вращение|вращения]], ячейки имели 2-, 3-, 4- или 6-кратную [[Вращательная симметрия|вращательную симметрию]]{{sfn|Cromwell|2009|с=36–56}}. |
|||
{{quote|The ideal form gracefully artificed suggests the infinite rising levels of existence and consciousness, expanding sizes rising toward transcendence above, and at the same time housing the sacred deep within{{sfn|Fractals in Indian Architecture}}Jackson{{sfn|Jackson}}}} |
|||
===Плитки гирих=== |
|||
{{Основная статья|Гирих (математика)}} |
|||
Начиная примерно с 1200-го года орнаменты гирих делались из звёзд и многоугольников, имеющих 5- или 10-кратную вращательную симметрию. Такие фигуры можно нарисовать с помощью циркуля и линейки. Однако, с 15-го века некоторые узоры гирих перестали быть периодическими и создавались с помощью [[Гирих (математика)|плиток гирих]]. Это набор из пяти плиток с нарисованными на них линиями. Плитки позволяют замостить плоскость без зазоров, при этом линии на плитках образуют орнамент гирих. Неизвестно, когда были использованы плитки гирих вместо построения с помощью [[Построение с помощью циркуля и линейки|циркуля и линейки]]. Принято считать, что плитки гирих были использованы в некоторых зданиях, построенных около 1200{{sfn|Lu, Steinhardt|2007|с=1106–1110}}. <ref>[http://www.physics.harvard.edu/~plu/publications/Science_315_1106_2007_SOM.pdf Lu and Steinhardt, Supplementary figures] {{webarchive|url=https://web.archive.org/web/20090326095515/http://www.physics.harvard.edu/~plu/publications/Science_315_1106_2007_SOM.pdf |date=2009-03-26 }}</ref> |
|||
[[Храм Минакши]] is a large complex with multiple shrines, with the streets of [[Мадурай]] laid out concentrically around it according to the shastras. The four gateways are tall towers ([[Гопурам|gopuram]]s) with Фрактал-like repetitive structure as at Хампи. The enclosures around each shrine are rectangular and surrounded by high stone walls{{sfn|King|2005|с=72}}. |
|||
====Ancient Greece==== |
|||
{{Подробно|Архитектура Древней Греции|Золотое сечение|Пифагореизм|Евклидова геометрия}} |
|||
[[Файл:The Parthenon Athens.jpg|thumb|left|The [[Парфенон]] was designed using [[Пифагореизм|Pythagorean]] ratios.]] |
|||
[[Pythagoras]] (c. 569 – c. 475 B.C.) and his followers, the Pythagoreans, held that «all things are numbers». They observed the harmonies produced by notes with specific small-integer ratios of frequency, and argued that buildings too should be designed with such ratios. The Greek word ''symmetria'' originally denoted the harmony of архитектурных shapes in precise ratios from a building's smallest details right up to its entire design{{sfn|O'Connor , Robertson|2002}}. |
|||
[[Файл:Parthenon-top-view.svg|thumb|upright|Floor plan of the Parthenon]] |
|||
[[Парфенон]] is {{convert|69.5|m|ft}} long, {{convert|30.9|m|ft}} wide and {{convert|13.7|m|ft}} high to the cornice. This gives a ratio of width to length of 4:9, and the same for height to width. Putting these together gives height:width:length of 16:36:81, or to the delight{{sfn|Maor|2007|с=19}} of the Pythagoreans 4<sup>2</sup>:6<sup>2</sup>:9<sup>2</sup>. This sets the module as 0.858 m. A 4:9 rectangle can be constructed as three contiguous rectangles with sides in the ratio 3:4. Each half-rectangle is then a convenient 3:4:5 right triangle, enabling the angles and sides to be checked with a suitably knotted rope. The inner area (naos) similarly has 4:9 proportions ({{convert|21.44|m|ft}} wide by 48.3 m long); the ratio between the diameter of the outer columns, {{convert|1.905|m|ft}}, and the spacing of their centres, {{convert|4.293|m|ft}}, is also 4:9{{sfn|O'Connor , Robertson|2002}}. |
|||
Парфенон is considered by authors such as [[Норвич, Джон|John Julius Norwich]] «the most perfect Doric temple ever built»{{sfn|Norwich|2001|с=63}}. Its elaborate архитектурных refinements include «a subtle correspondence between the Кривизна of the stylobate, the taper of the [[Целла|naos]] walls and the ''энтазис'' of the columns»{{sfn|Norwich|2001|с=63}}. ''[[Энтазис]]'' refers to the subtle diminution in diameter of the columns as they rise. The stylobate is the platform on which the columns stand. As in other classical Greek temples{{sfn|Penrose|1973|с=ch. II.3, plate 9}}, the platform has a slight parabolic upward Кривизна to shed rainwater and reinforce the building against earthquakes. The columns might therefore be supposed to lean outwards, but they actually lean slightly inwards so that if they carried on, they would meet about a mile above the centre of the building; since they are all the same height, the Кривизна of the outer stylobate edge is transmitted to the [[Архитрав]] and roof above: «all follow the rule of being built to delicate curves»{{sfn|Stevens|1962|с=337–338}}. |
|||
Золотое сечение was known in 300 B.C., when [[Евклид]] described the method of geometric construction.<ref>[[Начала (Евклид)|''Начала'' Евклида]]. Book 6, Proposition 30.</ref> It has been argued that the золотое сечение was used in the design of the Парфенон and other ancient Greek buildings, as well as sculptures, paintings, and vases{{sfn|Archibald}}. More recent authors such as Никос Салингарос, however, doubt all these claims.<ref>''[http://meandering-through-mathematics.blogspot.com/2012/02/applications-of-golden-mean-to.html Applications of the Golden Mean to Architecture]''</ref> Experiments by the computer scientist George Markowsky failed to find any preference for the [[Золотой прямоугольник]]{{sfn|Markowsky|1992}}. |
|||
====Исламская архитектура==== |
|||
{{Основная статья|Исламская архитектура}} |
|||
[[Файл:Alhambra - Patio de Leones - Status 2012.jpg|thumb|left|[[Львиный дворик]], [[Альгамбра]] has strict proportions based on [[Квадратный корень|square root]]s of small integers.]] |
|||
The historian of Islamic art Antonio Fernandez-Puertas suggests that the [[Альгамбра]], like the [[Мескита|Кóрдовская соборная мечеть в Кордове]] {{sfn|Gedal|2011}}, was designed using the [[Аль-Андалус|Hispano-Muslim]] foot or ''codo'' of about {{convert|0.62|m|ft}}. In the palace's [[Львиный дворик|львином дворике]], the proportions follow a series of [[Корень (математика)|радикалов]]. A rectangle with sides 1 and √2 has (by [[Теорема Пифагора|Pythagoras's theorem]]) a diagonal of √3, which describes the right triangle made by the sides of the court; the series continues with √4 (giving a 1:2 ratio), √5 and so on. The decorative patterns are similarly proportioned, √2 generating squares inside circles and eight-pointed stars, √3 generating six-pointed stars. There is no evidence to support earlier claims that золотое сечение was used in the Альгамбра{{sfn|Tennant|2003}}{{sfn|Irwin|2011|с=109–112}}. [[Львиный дворик |
|||
]] is bracketed by the Hall of Two Sisters and the Hall of the Abencerrajes; правильный [[шестиугольник]] can be drawn from the centres of these two halls and the four inside corners of the львиного дворика{{sfn|Robertson|2007}}. |
|||
[[Файл:Selimiye Mosque.png|thumb|upright|Мечеть Селимие, 1569–1575]] |
|||
[[Селимие (мечеть)|Мечеть Селимие]] в городе [[Эдирне]], Турция, was built by [[Синан|Мимаром Синаном]] to provide a space where the [[михраб]] could be see from anywhere inside the building. The very large central space is accordingly arranged as an восьмиугольник, formed by 8 enormous pillars, and capped by a circular dome of {{convert|31.25|m|ft}} diameter and {{convert|43|m|ft}} high. Восьмиугольник |
|||
is formed into a square with four semidomes, and externally by four exceptionally tall minarets, {{convert|83|m|ft}} tall. The building's plan is thus a circle inside восьмиугольника inside a square{{sfn|Blair, Bloom|1995}}. |
|||
====Mughal архитектура==== |
|||
{{Основная статья|Архитектура Великих Моголов|Фатехпур-Сикри|Источники и архитектура Тадж-Махал}} |
|||
[[Файл:TajMahalbyAmalMongia.jpg|thumb|left|Мавзолей |
|||
[[Тадж-Махал]] with part of the complex's gardens at [[Агра]]]] |
|||
[[Архитектура Великих Моголов]], as seen in the abandoned imperial city of [[Фатехпур-Сикри]] and the [[Тадж-Махал]] complex, has a distinctive mathematical order and a strong эстетика based on Симметрия and harmony{{sfn|Rai|1993|с=19–48}}{{sfn|Michell, Pasricha|2011}}. |
|||
Тадж-Махал exemplifies Mughal архитектуру, both representing [[рай]]{{sfn|Parker|2010|с=224}} and displaying the [[Список падишахов Могольской империи|Mughal Emperor]] [[Шах-Джахан|Шах-Джахан]]'s power through its scale, Симметрия and costly decoration. The white marble [[мавзолей]], decorated with {{не переведено 5|Флорентийская мозаика|||pietra dura}}, the great gate (''Darwaza-i rauza''), other buildings, the gardens and paths together form a unified hierarchical design. The buildings include a [[мечеть]] in red sandstone on the west, and an almost identical building, the Jawab or 'answer' on the east to maintain the bilateral Симметрия of the complex. The formal {{не переведено 5|Чарбах|||charbagh}} ('сад в четырёх частях') is in four parts, symbolising the four rivers of paradise, and offering views and reflections of the мавзолея. These are divided in turn into 16 parterres{{sfn|Koch|2006|с=24 and passim}}. |
|||
[[Файл:Taj site plan.png|thumb|upright=1.5|Site plan of Тадж-Махал complex. The great gate is at the right, the Мавзолей in the centre, bracketed by the Мечеть (below) and the jawab. The plan includes squares and [[восьмиугольник]]и.]] |
|||
Тадж-Махал complex was laid out on a grid, subdivided into smaller grids. The historians of архитектуры Koch and Barraud agree with the traditional accounts that give the width of the complex as 374 Mughal yards or [[Зира (единица длины)|зира]],{{efn|1 gaz is about {{convert|0.86|m|ft}}.}} the main area being three 374-gaz squares. These were divided in areas like the bazaar and caravanserai into 17-gaz modules; the garden and terraces are in modules of 23 зиры, and are 368 зир wide (16 x 23). Мавзолей, мечеть and guest house are laid out on a grid of 7 зир. Koch and Barraud observe that if восьмиугольник, used repeatedly in the complex, is given sides of 7 units, then it has a width of 17 units,{{efn|A square drawn around восьмиугольника by prolonging alternate sides adds four right angle triangles with hypotenuse of 7 and the other two sides of √(49/2) or 4,9497..., nearly 5. The side of the square is thus 5+7+5, which is 17.}} which may help to explain the choice of ratios in the complex{{sfn|Koch|2006|с=104–109}}. |
|||
====Христианская архитектура==== |
|||
{{Подробно|Архитектура церквей}} |
|||
[[Файл:Hagia-Sophia-Grundriss.jpg|thumb|upright=1.4|[[ Собор Святой Софии (Константинополь)|Собор Святой Софии]], Стамбул<br>a) Plan of gallery (upper half)<br>b) Plan of the ground floor (lower half)]] |
|||
[[Христианин|Христианская]] [[Патриарх Константинопольский|патриаршая]] [[базилика]] [[Собор Святой Софии (Константинополь)|собора Святой Софии]] в городе [[Византий]] (ныне [[Стамбул]]), построенный в 537 (и дважды перестроенный), был в течение тысячи лет{{efn|Вплоть до того, как [[Севильский кафедральный собор]] был завершён в 1520.}} наибольшим кафедральным собором. Он стимулировал построение многих более поздних зданий, включая [[Голубая мечеть (Стамбул)|Мечеть Султанахмет]] и другие мечети города. [[Архитектура Византии]] включает притвор, увенчанный круглым куполом и два полукуполами, все одного диаметра (31м), с пятью меньшими полукуполами, образующими [[Апсида|апсиду]] и четыре круглых угла просторного прямоугольного внутреннего пространства{{sfn|Fazio, Moffett, Wodehouse|2009}}. Это интерпретировалось средневековыми архитекторами как представление земного внизу (квадратное основание) и святых небес сверху (устремлённый ввысь сферический купол){{sfn|Gamwell|2015|с=48}}. Император [[Юстиниан I]] использовал двух геометров, [[Исидор Милетский|Исидора Милетского]] и [[Анфимий из Тралл|Исидора Милетского]] в качестве архитекторов. Исидор собрал труды [[Архимед]]а по [[Стереометрия|стереометрии]] и был под его влиянием{{sfn|O'Connor , Robertson|2002}}{{sfn|Kleiner, Mamiya|2008|с=329}}. |
|||
Важность [[Крещение|крещения]] в воде в христианстве была отражена в архитектуре [[баптистерий]]. Наиболее старый, [[Латеранский баптистерий]] в Риме, построеных в 440{{sfn|Menander, Brandt, Appetechia, Thorén|2010}}, установил тенденцию восьмиугольных баптистерий. [[Купель]] внутри этих строений была часто восьмиугольной, хотя наиболее крупный итальянский [[баптистерий в Пизе]], построенный между 1152 и 1363, имеет круглую форму с восьмиугольным резервуаром. Баптистерий имеет высоту 54,86 метра с диаметром 34,13 метра (отношение 8:5){{sfn|The Baptistery}}. [[Амвросий Медиоланский]] писал, что резервуары и баптистерии имели восьмиугольную форму, «поскольку на восьмой день{{efn|Шестой день [[Страстная седмица|cтрастной седмицы]] был [[Великая пятница|Великой пятницей]]. Последующие воскресенье ([[Воскресение из мёртвых|воскрешение]]) было, таким образом восьмым днём{{sfn|Huyser-Konig}}.}} было вознесение, Христос ослабляет оковы смерти и получает мёртвых из их могил.»{{sfn|Huyser-Konig}}{{sfn|Kuehn|1992|с=53–60}}. |
|||
[[Аврелий Августин]] аналогично описывает восемь дней как «вечность ... освящёння [[Воскресение из мёртвых|воскрешением]] Христа»{{sfn|Kuehn|1992|с=53–60}}{{sfn|Augustine of Hippo|426|с=Book 22, Chapter 30}}. Восьмиугольный [[Флорентийский баптистерий|баптистерий Сент-Джона, Флоренция]], построенный между 1059 и 1128, одно из наиболее старых зданий в городе, и одно из последних прямых традиций античности. Оно крайне сильно повлияло на флорентийских архитекторов и главные архитекторы той эпохи, включая [[Таленти, Франческо|Франческо Таленти]], Alberti and Brunelleschi used it as the model of classical архитектуры{{sfn|Kleiner|2012|с=355–356}}. |
|||
The number five is used «exuberantly»{{sfn|Simitch, Warke|2014|с=191}} in the 1721 [[Церковь Святого Иоанна Непомука]] at Zelená hora, near [[Ждяр-над-Сазавоу]] in the Czech republic, designed by [[Сантини, Ян|Jan Blažej Santini Aichel]]. The nave is circular, surrounded by five pairs of columns and five oval domes alternating with ogival апсиды. The church further has five gates, five chapels, five altars and five stars; a legend claims that when [[Ян Непомуцкий]] was martyred, five stars appeared over his head{{sfn|Simitch, Warke|2014|с=191}}{{sfn|Zelená hora}}. The fivefold архитектура may also symbolise the {{не переведено 5|Пять ран Христа|||five wounds of Christ}} and the five letters of «Tacui» (Latin: «я храню молчание» [about secrets of the [[Исповедальня|исповедальни]]]){{sfn|Saint John of Nepomuk}}. |
|||
[[Гауди, Антонио|Antoni Gaudí]] used a wide variety of geometric structures, some being Минимальная поверхностьs, in the [[Саграда-Фамилия]], [[Барселона]], started in 1882 (and not completed as of 2015). These include hyperbolic [[Параболоид]]s and [[Гиперболоид|hyperboloids of revolution]],{{sfn|Burry, Burry, Dunlop, Maher|2001|}} замощений, {{не переведено 5|Арка с очертанием обратной цепной линии|||catenary arch}}es, [[Катеноид]]s, [[Геликоид]]s, and [[Линейчатая поверхность|ruled surface]]s. This varied mix of geometries is creatively combined in different ways around the church. For example, in the Passion Façade of Саграда-Фамилия, Gaudí assembled stone «branches» in the form of hyperbolic Параболоидs, which overlap at their tops (directrices) without, therefore, meeting at a point. In contrast, in the colonnade there are hyperbolic Параболоидal surfaces that smoothly join other structures to form unbounded surfaces. Further, Gaudí exploits [[Закономерности в природе|natural patterns]], themselves mathematical, with [[Колонна (архитектура)|колоннами]] derived from the shapes of [[Дерево|tree]]s, and [[Притолока|lintel]]s made from unmodified [[Базальт|basalt]] naturally cracked (by cooling from molten rock) into {{не переведено 5|Список мест со столбами около вулкана|шестиугольных столбов]||List of places with columnar jointed volcanic}}{{sfn|Geometry of Antoni Gaudi}}{{sfn|Usvat}}{{sfn|Burry, Burry, Dunlop, Maher|2001}}. |
|||
The 1971 {{не переведено 5|Собор Успения Святой Марии|Собор Успения Святой Марии, Сан-Франциско||Cathedral of Saint Mary of the Assumption (San Francisco, California)}} has a [[двускатная крыша]] composed of eight segments of hyperbolic Параболоидs, arranged so that the bottom horizontal cross section of the roof is a square and the top cross section is a [[Крест в христианстве|Christian cross]]. The building is a square {{convert|77.7|m|ft}} on a side, and {{convert|57.9|m|ft}} high{{sfn|Nervi}}. The 1970 [[Кафедральный собор (Бразилиа)|Cathedral of Brasília]] by [[Нимейер, Оскар|Oscar Niemeyer]] makes a different use of a Гиперболоид structure; it is constructed from 16 identical concrete beams, each weighing 90 tonnes,{{efn|This is {{convert|90|t|ton}}.}} arranged in a circle to form Гиперболоид вращения, the white beams creating a shape like hands praying to heaven. Only the dome is visible from outside: most of the building is below ground{{sfn|Brasilia Cathedral}}{{sfn|Behrends, Crato, Rodrigues|2012|с=143}}{{sfn|Emmer|2012|с=111}}{{sfn|Mkrtchyan|2013}}. |
|||
Several medieval {{не переведено 5|Северные круглые церкви|церкви в Скандинавии являются круглыми||Nordic round churches}}, including four on the Danish island of [[Борнхольм|Bornholm]]. One of the oldest of these, {{не переведено 5|Эстерларская церковь|||Østerlars Church}} from c. 1160, has a circular nave around a massive circular stone column, pierced with arches and decorated with a fresco. The circular structure has three storeys and was apparently fortified, the top storey having served for defence{{sfn|Nordens kirker}}{{sfn|Natur Bornholm}} |
|||
<gallery> |
<gallery> |
||
File:Istanbul 036 (6498284165).jpg|The vaulting of the nave of [[Собор Святой Софии (Константинополь)|Собор Святой Софии]], Стамбул ''([[Commons:File:Istanbul 036 (6498284165).jpg|annotations]]''), 562 |
|||
Girih tiles.svg|Плитки гирих |
|||
File:Battistero Firenze.jpg|Восьмиугольный [[Флорентийский баптистерий|Baptistry of Saint John, Florence]], completed in 1128 |
|||
Green_mosque_girih.png|Гирих орнамент, сделанный из плиток гирих |
|||
File:Jan Santini Aichel - Zelená Hora ground plan 2.jpg|Fivefold symmetries: [[Сантини, Ян|Jan Santini Aichel]]'s [[Церковь Святого Иоанна Непомука]] at Zelená hora, 1721 |
|||
Green_mosque_archway.JPG|Деталь [[Зелёная мечеть|Зелёной мечети]] (Бурса, Турция), использующая этот орнамент |
|||
File:Sagfampassion.jpg|Passion façade of [[Гауди, Антонио|Antoni Gaudí]]'s [[Саграда-Фамилия]], [[Барселона]], started 1882 |
|||
File:Brazil.Brasilia.01.jpg|[[ Нимейер, Оскар|Oscar Niemeyer]]'s [[Кафедральный собор (Бразилиа)|Cathedral of Brasília]], 1970 |
|||
File:St Mary's Cathedral - San Francisco.jpg|{{не переведено 5|Собор Успения Святой Марии|Собор Успения Святой Марии, Сан-Франциско||Cathedral of Saint Mary of the Assumption (San Francisco, California)}}, 1971 |
|||
File:Oesterlarsfresco.jpg|Central column of {{не переведено 5|Эстерларская церковь|Эстерлара||Østerlars Church}} {{не переведено 5|Северные круглые церкви|||Nordic round churches}} in [[Борнхольм|Bornholm]], Denmark |
|||
</gallery> |
</gallery> |
||
==Математическое украшение== |
|||
====Двухуровневые орнаменты ==== |
|||
{{Кратное изображение|зона=right|изобр1=Darb-i Imam shrine spandrel.JPG|ширина1=125 |
|||
|подпись1=Орнамент гирих на [[Пазуха сводов|сводах]] в храме [[Дарбе-имам]], Исфаха, Иран. |
|||
|изобр2=Spandrel-large scale pattern.svg|ширина2=125| |
|||
|подпись2=Реконструкция большего орнамента с большими плитками гирих. Контуры пазухи свода показаны жёлтой пунктирной линией. |
|||
|изобр3=Darbeimam subdivision rule.svg|ширина3=125| |
|||
|подпись3=Правило подразделения, используемое для генерации орнамента гириха на пазухе свода. Большие десятиугольные плитки и плитки в виде галстука-бабочки подразделяются на меньшие плитки гирих. В истинных пазухах свода линии малых плиток заполнены чёрным (вверху слева)}} |
|||
===Исламское архитектурный декор=== |
|||
Орнаменты гирих на храме [[Дарбе-имам]], построенном в 1453 в [[Исфахан]]е, имеет много более сложные узоры чем были видны до этого времени. Детали орнамента показывают, что для украшения храма использовались плитки гирих, а не узоры, построенные с помощью циркуля и линейки. Орнаменты этого храма [[Периодическая функция|апериодичны]]. То есть, на стене они не образуют повторяющегося узора. Другая характеристика орнаментов на храме Дарбе-имам заключается в том, что орнаменты нарисованы в двух различных масштабах. Бо́льшие орнаменты заметны на расстоянии, в то время как более мелкие узоры, являющиеся частями крупных орнаментов, заметны вблизи здания{{sfn|Lu, Steinhardt|2007|с=1106–1110}}. |
|||
{{Основная статья|Исламские геометрические орнаменты}} |
|||
[[Файл:Sally Port of Sheikh Lotf Allah Mosque.JPG|thumb|The complex геометрия and tilings of the [[Сотовый свод|muqarnas]] vaulting in the [[Мечеть шейха Лотфоллы|Sheikh Lotfollah Mosque]], [[Исфахан]], 1603–1619]] |
|||
Хотя есть свидетельства, что некоторые древние мозаики гирих использовали [[Конечное правило подразделения|правило подразделения]] для создания двухуровневых узоров, неизвестно никаких исторических примеров использования правил подразделения, которые могут быть применены бесконечное число раз. Например, орнамент, использованный в пазухе сводов храма Дарбе-имам (см. рисунок) состоит только из десятиугольников и плиток в виде галстука-бабочки, в то время как правил подразделения использует кроме этих двух плиток удлинённую шестиугольную плитку. Таким образом, этот орнамент не проявляет самоподобность между уровнями 1 и 2. Однако, плитки рисунка, содержащего десятиугольники, получается путём повторяющегося применения правила подразделения реализуется в [[Квазикристалл|квазикристаллическом замощении]]{{sfn|Lu, Steinhardt|2007|с=1106–1110}}. |
|||
Исламские здания часто украшаются {{не переведено 5|Исламские геометрические орнаменты|геометрическими орнаментами||Islamic geometric patterns}}, в которых, как правило, используются математические [[Паркет (геометрия)|мозаики]], образованные керамическими плитками ([[гирих]], [[Зулляйдж]]), которые могут быть сами по себе быть простыми или украшены полосками{{sfn|O'Connor , Robertson|2002}}.В исламских орнаментах используются смметричные фигуры, такие как звёзды с шестью, восемью или кратные восьми точки. Некоторые из них основываются на мотивах печати Соломона, восьмиугольной звезды, сделанной из двух квадратов, повёрнутых на 45 градусов относительно друг друга{{sfn|Rønning}}. Исламские орнаменты используют многие из 17 возможных {{не переведено 5|Группа обоев|групп обоев||wallpaper groups}}. В 1944 Эдит Мюллер показала, что в украшении ансамбля Альгамбра используется 11 групп обоев, а в 1986 [[Грюнбаум, Бранко|Бранко Грюнбаум]] заявил, что нашёл 13 групп обоев в Альгамбра, настаивая при этом, что оставшиеся 4 группы не были найдены нигде в исламских орнаментах {{sfn|Rønning}}. |
|||
====Апериодичность==== |
|||
Периодическое замощение плоскости — это регулярное повторение «единичной ячейки» (повторяющейся фигуры или группы фигур) без зазоров. Такие упаковки можно видеть в двумерных кристаллах и вследствие {{не переведено 5|Теорема о кристаллографических ограничениях|теоремы о кристаллографических ограничениях||Crystallographic restriction theorem}}, единичная ячейка ограничена 2-, 3-, 4- или 6-кратными вращательными симметриями. По этой причине невозможно замостить плоскость периодически фигурами, имеющими пятикратную вращательную симметрию, такими как пятиугольная звезда или десятиугольник. Орнаменты с бесконечными совершенными квазипериодическим порядком переноса могут иметь запрещённые кристаллографией симметрии, какие имеют пятиугольники и десятиугольники. Такие фигуры с пятикратной симметрией повторяются периодически, хотя пространство между ними содержит другие фигуры, которые не имеют периодического орнамента. Такие замощения называются квазикристаллическими{{sfn|Lu, Steinhardt|2007|с=1106–1110}}. |
|||
===Современное архитектурное украшение === |
|||
Один из способов построения квазипериодических мозаик — создание [[Мозаика Пенроуза|мозаики Пенроуза]]. Плитки гирих можно разделить в плитки Пенроуза, называемые «дротик» и «змей», но нет никаких свидетелств, что этот подход был использован средневековыми художниками{{sfn|Lu, Steinhardt|2007|с=1106–1110}}. Другой способ построения квазипериодических мозаик — подразделение плиток гирих на более мелкие плитки гирих с использованием [[Конечное правило подразделения|правила подразделения]]. В пределе плоскость будет разделена на плитки гирих, которые повторяются в частоте использования, но не образуют периодической мозаики. Применение такого правила подразделения могло бы свидетельствовать, что исламские художники 15-го века старарались, чтобы созданные из плиток гирих орнаменты никогда не повторялись. Однако, все известные орнаменты гирих, сделанные из плиток гирих показывают уровень не больше второго. Фактически, не требовалось на практике, чтобы орнамент давал более двух уровней рисунка, поскольку третий уровень был бы либо слишком крупным, либо слишком мелким. Похоже, следневековые исламские художники обладали инструментом создания очень сложных орнаментов, но никогда его не использовали. Как говорил Маковицкий{{sfn|Makovicky|2007|с=1383}}, |
|||
{{Подробно|Орнамент|Aрхитектура 21-го века}} |
|||
{{Blockquote|text=Художники были удовлетворены созданием больших фундаментальных областей, но не заботились о математическом понятии бесконечно расширяемых квазипериодических рисунков. Однако они понимали и использовали некоторые локальные геометрические свойства квазикристаллических орнаментов.|author=Маковицкий}} |
|||
К концу 20-го века новые математические конструкции, такие как фрактальная геометрия and апериодичные замощения были подхвачены архитекторами для обеспечения интересной и привлекательной облицовки зданий {{sfn|Williams, Ostwald|2015|с=1-24, chapter 48}}. В 1913, архитектор-модернист [[Лоз, Адольф|Адольф Лоз]] провозгласил: «Орнамент — это преступление»{{sfn|Gibberd, Hill|2013}}, оказав влияние на архитектурное мышление до конца 20-го века. В 21-м веке архитекторы снова начали использовать [[орнамент]]ы. Орнаменты 21-го века сильно отличаются. [[Харпа|Концертный зал и конференц-центр]] {{не переведено 5|Ларсен, Хеннинг|Хеннинга Ларсена||Henning Larsen}} 2011года в Рейкьявике выглядит подобно стене из кристаллов и сделан из больших блоков стекла{{sfn|Gibberd, Hill|2013}}. Здание Форейн Оффис Аркитект 2010-го года {{не переведено 5|Равенсборнский колледж|Равенсборнского колледжа||Ravensbourne College}} в Лондоне покрыт 28,000 анодированными алюминиевыми плитками красного, белого и коричневого цветов, связывая круглые окна различных размеров. Покрытие использует три типа плитки — равносторонний треугольник и два неправильных пятиугольника{{sfn|Ravensbourne College|2010}}{{sfn|Bizley}}{{efn|Предполагалось апериодичное замозение, чтобы избежать ритма в решётке, но, на практике, [[мозаика Пенроуза]] была слишком сложной, так что была выбрана решётка рсзмером 2,625м по горизонтали и 4,55м по вертикали {{sfn|Bizley}}.}} {{не переведено 5|Библиотека в Канадзаве|||Kanazawa Umimirai Library}} (архитекторы Кадзуми Кудо и Хироси Хориба из Coelacanth K&H Architects ) имеет декоративную решётку сделанную из маленьких круглых блоков стекла, вставленных в плоские бетонные стены {{sfn|Gibberd, Hill|2013}}. |
|||
====Свиток Топкапы==== |
|||
[[Файл:Panel50.PNG|thumb|right|100px|Панель со {{не переведено 5|Свиток Топкапы|свитка Топкапы||Topkapı Scroll}}. Чёрные линии показывают орнамент гирих, тонкие красные линии показывают контуры плиток гирих.]] |
|||
{{не переведено 5|Свиток Топкапы|||Topkapı Scroll}} с конца 15-го века, показывающий, что плитки гирих были использованы для создания орнаментов гирих. Рисунки этих орнаментов в книге показывают линии гирих с наложенными линиями плиток, использованных для образования орнаментов гирих{{sfn|Lu, Steinhardt|2007|с=1106–1110}}. |
|||
<gallery> |
<gallery> |
||
File:London MMB «T1 Ravensbourne College.jpg|{{не переведено 5|Равенсборнский колледж|||Ravensbourne College}}, Лондон, 2010 |
|||
Panel29.JPG|Панель из свитка Топкапы, показывающей орнаменты гирих двух различных масштабов и плитки гирих для их построения. |
|||
File:Harpa.JPG|[[Харпа|Концертный зал и конференц-центр]], Исландия, 2011 |
|||
Panel28a.PNG|Реконструкция малого орнамента (толстые чёрные линии) с левой панели, использующего малые плитки гирих. |
|||
File:Umimirai Library.jpg|{{не переведено 5|Библиотека в Канадзаве|||Kanazawa Umimirai Library}}, Japan, 2011 |
|||
Panel28b.PNG|Реконструкция большого орнамента (толстые красные линии) с левой панели, использующего боьшие плитки гирих. |
|||
File:Museo Soumaya Plaza Carso V.jpg|[[Соумайя|Музей искусства Соумайя]], Мехико, 2011 |
|||
</gallery> |
</gallery> |
||
==Крепости== |
|||
==Галерея== |
|||
===Европа=== |
|||
{{Подробно|Бастионная система укреплений}} |
|||
Архитектура [[Фортификационное сооружение|фортификационных сооружений]] эволюционировала из {{не переведено 5||Средневековые укрепления|средневековых укреплений|medieval fortification}, которые имели высокие каменные стены, к низкой симметричной [[Бастионная система укреплений|бастионным системам укреплений]], способных сопротивляться [[Артиллерия|артиллерийскому]] обстрелу между середины пятнадцатого и девятнадцатым веками. Геометрия звёздной формы диктовалась необходимостью не допустить мёртвых зон, в которых атакующая пехота могла бы укрыться от огня защищающейся стороны. Стороны выступающих точек образовывали угол для возможности покрытия огнём всю поверхность и позволяли перекрёстный огонь (с двух сторон) с каждой выступающей точки. Хорошо известны архитекторы, разрабатывающие такую защиту, — [[Микеланджело]], [[Перуцци, Бальдассаре|Бальдассаре Перуцци]], [[Скамоцци, Винченцо|Винченцо Скамоцци]] и [[Вобан, Себастьен Ле Претр де| Себастьен Ле Претр де Вобан]]{{sfn|Duffy|1975}}{{sfn|Chandler|1990}}. |
|||
Историк архитектуры [[Зигфрид Гидион]] говорил, что фортификационные сооружения в виде звёзд имели определяющее влияние на компоновку [[Градостроительство|идеальных городов]] эпохи возрождения: «Эпоха возрождения была загипнотизирована одним типом городов, который в течение полутора веков — от Филарета до Скамоцци — был отпечатком всех утопических схем, это был город в виде звезды.»{{sfn|Giedion|1962|с=43}}. |
|||
<gallery> |
<gallery> |
||
File:Coevorden.jpg|[[Куворден]] План фортификационного сооружения 17-го века |
|||
File:Salim Chishti Tomb-2.jpg |
|||
File:Palmanova1600.jpg|[[Пальманова]], [[Италия]], [[Венецианская республика|Венецианский]] город с a [[Бастионная система укреплений|бастионной системой укреплений]]. 17-й век |
|||
File:Kayseri Hunat Hatun Complex3-Verity Cridland.jpg |
|||
File:Neuf-Brisach 007 850.jpg|[[ Нёф-Бризах]], [[Эльзас]], одно из {{не переведено 5|Фортификационное сооружение Вобана|фортификационных сооружений Вобана||Fortifications of Vauban}} |
|||
File:Flickr - HuTect ShOts - Pattern of The Tomb Gate - Masjid of Sultan Hassan مسجد ومدرسة السلطان حسن - Cairo - Egypt - 28 05 2010.jpg |
|||
File:Lacería.jpg |
|||
</gallery> |
</gallery> |
||
===Китай=== |
|||
[[Файл:HakkaYongding.jpg|thumb|A [[тулоу]] in {{не переведено 5|Уезд Юндин|уезде Юндин||Yongding County}}, [[Фуцзянь|провинция Фуцзянь]]]] |
|||
В [[Архитектура Китая|архитектуре Китая]] [[тулоу]] [[Фуцзянь|провинции Фуцзян]] — это круглые структуры общественной защиты, главным образом, с сплошными стенами и одной покрытой железом деревянной дверью, датируемые шестнадцатым веком. Стены покрыты крышами, которые немного наклонены во внешнюю и внутренние стороны, образуя кольцо. Центр кольца является открытым мощёным внутренним двором, часто со стеной, окружающей укреплённые галереи высотой до пяти этажей {{sfn|O'Neill|2015}}. |
|||
==Экологические цели== |
|||
[[Файл:Yakhchal of Yazd province.jpg|thumb|left|{{не переведено 5|Якчхал|||yakhchal}} в городе [[Йезд]], Иран]] |
|||
Архитекторы могут также выбирать форму здания из экологических соображений{{sfn|Simitch, Warke|2014|с=191}}. Например, [[Небоскрёб Мэри-Экс]] архитектурного бюро [[Foster and Partners]], Лондон, известный как «Корнишон» за его подобную [[Огурец обыкновенный|огурцу]] форму, является [[Тела вращения|телом вращения]], разработанный с использованием [[Система автоматизированного проектирования|системы автоматизированного проектирования]]. Геометрия здания была выбрана не только исходя из эстетических причин, а чтобы минимизировать вихри воздуха у основания здания. Вопреки явно кривой поверхности, все панели стекла, образующие поверхность, являются плоскими, за исключением линзы на вершине здания. Большинство панелей квадратны, поскольку это позволяет вырезать стёкла с меньшими отходами{{sfn|Freiberger|2007}}. |
|||
Традиционный {{не переведено 5|якчхал|||yakhchal}} (ледяная яма) в [[Иран|Персии]] функционирует подобно [[Испарительный охладитель|испарительного охладителя]]. Над поверхностью структура имеет вид купола, но имеет подземное место хранения для льда, а иногда и для пищи. Подземное пространство и толстая теплонепроницаемая конструкция изолирует пространство круглый год. Внутреннее пространство часто остужалось [[Бадгир|ветроуловителями]]. Лёд был доступен летом для приготовления холодного десерта [[фалуде]]{{sfn|Mahdavinejad, Javanrudi|2012}}. |
|||
==См. также== |
|||
* [[Математика и изобразительное искусство]] |
|||
* [[Закономерности в природе]] |
|||
Пояснения |
|||
{{notelist}} |
|||
==Примечания== |
==Примечания== |
||
| Строка 95: | Строка 249: | ||
{{refbegin|colwidth=30em}} |
{{refbegin|colwidth=30em}} |
||
*{{статья |
*{{статья |
||
|автор= Iasef Md Rian, Jin-Ho Park, Hyung Uk Ahn, Dongkuk Chang |
|||
|автор=Lee A.J. |
|||
|ref=Rian, Park, Ahn, Chang |
|||
|ref=Lee |
|||
|заглавие=Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho |
|||
|заглавие=Islamic Star Patterns |
|||
|издание= |
|издание=Building and Environment |
||
|год=2007 |
|||
|страницы=182–197 |
|||
|том=42 |
|||
|jstor=1523103 |
|||
|ссылка=http://www.academia.edu/7482254/Fractal_geometry_as_the_synthesis_of_Hindu_cosmology_in_Kandariya_Mahadev_temple_Khajuraho|doi=10.1016/j.buildenv.2007.01.028 |
|||
|том=4 |
|||
}} |
|||
|год=1987 |
|||
*{{cite web |
|||
|title=Architectural Engineering Overview |
|||
|ref=Overview |
|||
|url=http://dl4a.org/uploads/pdf/archeng.pdf |
|||
|publisher=Sloan Career Cornerstone Center |
|||
|accessdate=27 October 2017 |
|||
}} |
|||
*{{книга |
|||
|автор=Michael Leyton |
|||
|ref=Leyton |
|||
|заглавие=A Generative Theory of Shape |
|||
|год=2001 |
|||
|издательство=Springer |
|||
|isbn=978-3-540-42717-9 |
|||
}} |
|||
*{{книга |
|||
|автор=Alexey Stakhov, Olsen Olsen |
|||
|ref=Stakhov, Olsen |
|||
|заглавие=The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science |
|||
|год=2009 |
|||
|издательство=World Scientific |
|||
|isbn=978-981-277-582-5 |
|||
}} |
|||
*{{книга |
|||
|автор=William Smith |
|||
|ref=Smith |
|||
|заглавие=[[Dictionary of Greek and Roman Biography and Mythology]] |
|||
|год=1870 |
|||
|издательство=Little, Brown |
|||
|страницы=620 |
|||
}} |
|||
* {{статья |
|||
|автор=Saskia van den Hoeven, Maartje van der Veen |
|||
|ref=van den Hoeven, van der Veen |
|||
|заглавие=Muqarnas: Mathematics in Islamic Arts |
|||
|ссылка=http://www.jphogendijk.nl/projects/muqarnas2010.pdf |
|||
|издательство=Utrecht University |
|||
|accessdate=30 September 2015 |
|||
|год=2010 |
|||
}} |
|||
*{{книга |
|||
|автор=Felipe Cucker |
|||
|ref=Cucker |
|||
|заглавие=Manifold Mirrors: The Crossing Paths of the Arts and Mathematics |
|||
|год=2013 |
|||
|издательство=Cambridge University Press |
|||
|isbn=978-0-521-72876-8 |
|||
|страницы=103–106 |
|||
}} |
|||
*{{книга |
|||
|ответственный=Kim Williams, Michael J. Ostwald |
|||
||ref=Williams, Ostwald |
|||
|заглавие=Architecture and Mathematics from Antiquity to the Future: Volume I: from Antiquity to the 1500s |
|||
|издательство=Birkhäuser |
|||
|год=2015 |
|||
|isbn=978-3-319-00136-4 |
|||
|страницы=chapter 1. 1–24 |
|||
}} |
|||
*{{книга |
|||
|ответственный=Kim Williams, Michael J. Ostwald |
|||
||ref=Williams, Ostwald |
|||
|заглавие=Architecture and Mathematics from Antiquity to the Future Volume II: The 1500s to the Future |
|||
|издательство=Birkhäuser |
|||
|год=2015 |
|||
|isbn=978-3-319-00142-5 |
|||
}} |
|||
*{{cite web |
|||
|author=Vitruvius |
|||
|title=VITRUVIUS, BOOK IV, CHAPTER 3 On the Doric order |
|||
|url=http://www.vitruvius.be/boek4h3.htm |
|||
|website=Vitruvius.be |
|||
|accessdate=6 October 2015 |
|||
}} |
|||
*{{книга |
|||
|автор=Vitruvius |
|||
|ref=Vitruvius |
|||
|заглавие=On Architecture |
|||
|ссылка=https://books.google.com/books?id=lBLNbOp46CYC&pg=PR9 |
|||
|год=2009 |
|||
|издательство=Penguin Books |
|||
|isbn=978-0-14-193195-1 |
|||
}} |
|||
*{{книга |
|||
|автор=Kim Williams, Michael J. Ostwald |
|||
|ref=Williams, Ostwald |
|||
|заглавие=Architecture and Mathematics from Antiquity to the Future Volume I: Antiquity to the 1500s |
|||
|ссылка=https://books.google.com/books?id=fWKYBgAAQBAJ&pg=PA42 |
|||
|месяц=February |
|||
|год=2015 |
|||
|издательство=Birkhäuser |
|||
|isbn=978-3-319-00137-1 |
|||
}} |
|||
*{{книга |
|||
|автор=Leland M. Roth |
|||
|ref=Roth |
|||
|заглавие=Understanding Architecture: Its Elements, History, And Meaning |
|||
|издательство=Westview Press |
|||
|место=Boulder |
|||
|год=1992 |
|||
|isbn=0-06-438493-4 |
|||
}} |
|||
*{{книга |
|||
|автор=Amanda Claridge |
|||
|ref=Claridge |
|||
|заглавие=Rome |
|||
|серия=Oxford Archaeological Guides |
|||
|издательство=Oxford University Press |
|||
|место=Oxford Oxfordshire |
|||
|год=1998 |
|||
|isbn=0-19-288003-9 |
|||
}} |
|||
*{{книга |
|||
|автор=Lynne C. Lancaster |
|||
|ref=Lancaster |
|||
|заглавие=Concrete Vaulted Construction in Imperial Rome: Innovations in Context |
|||
|издательство=Cambridge University Press |
|||
|место=Cambridge |
|||
|год=2005 |
|||
|isbn=0-521-84202-6 |
|||
|страницы=44–46 |
|||
}} |
}} |
||
*{{статья |
*{{статья |
||
|автор=Lionel March |
|||
|заглавие=Notes on a recent study of the Topkapı scroll: a review article |
|||
|ref=March |
|||
|автор=Rogers J.M. |
|||
|заглавие=Renaissance mathematics and architectural proportion in Alberti's De re aedificatoria |
|||
|ref=Rogers |
|||
|издание=Architectural Research Quarterly |
|||
|издание=Bulletin of the School of Oriental and African Studies, University of London |
|||
|год=1996 |
|||
|том= 60 |
|||
|том=2 |
|||
|выпуск= 3 |
|||
|выпуск=1 |
|||
|страницы=433–439 |
|||
|страницы=54–65 |
|||
|год=1997 |
|||
|doi=10.1017/S135913550000110X |
|||
|jstor=619536 |
|||
}} |
|||
|doi=10.1017/s0041977x0003247x |
|||
*{{cite web |
|||
|ref=Mathalino.com |
|||
|title=Sphere circumscribing a cube |
|||
|url=http://www.mathalino.com/reviewer/solid-mensuration-solid-geometry/013-insciribed-and-circumscribed-sphere-about-cube-volume- |
|||
|website=Mathalino.com Engineering Math Review |
|||
|accessdate=4 October 2015 |
|||
}} |
}} |
||
*{{книга |
*{{книга |
||
|автор= |
|автор=Kirsti Andersen |
||
|ref= |
|ref=Andersen |
||
|заглавие=The Geometry of an Art: The History of the Mathematical Theory of Perspective from Alberti to Monge |
|||
|заглавие=Islamic Geometric Patterns |
|||
|ссылка=https://books.google.com/books?id=8B_JeMxNUIkC&pg=PA120 |
|||
|издательство=[[Thames and Hudson]] |
|||
|год=2008 |
|год=2008 |
||
|издательство=Springer |
|||
|isbn=978-0-500-28721-7 |
|||
|isbn=978-0-387-48946-9 |
|||
}} |
|||
*{{статья |
|||
|автор=Carsten Ruhl |
|||
|ref=Ruhl |
|||
|заглавие=Palladianism: From the Italian Villa to International Architecture |
|||
|ссылка=http://ieg-ego.eu/en/threads/europe-on-the-road/educational-journey-grand-tour/carsten-ruhl-palladianism |
|||
|издательство=European History Online |
|||
|accessdate=3 October 2015 |
|||
|месяц=April |
|||
|год=2011 |
|||
}} |
}} |
||
*{{книга |
*{{книга |
||
|автор=Trewin Copplestone |
|||
|заглавие=The transformation of Islamic art during the Sunni revival |
|||
|ref=Copplestone |
|||
|автор=Yasser Tabbaa |
|||
|год=1963 |
|||
|ref=Tabbaa |
|||
|заглавие=World Architecture |
|||
|год=2002 |
|||
|издательство= |
|издательство=Hamlyn |
||
|страницы=84 |
|||
|ссылка=https://books.google.com/books?id=ph7EdrzSpGoC&pg=PA84 |
|||
|isbn= 978-1-85043-392-7 |
|||
}} |
}} |
||
*{{статья |
*{{статья |
||
|автор= |
|автор=Stephen R. Wassell |
||
|ref= |
|ref=Wassell |
||
|заглавие=The Mathematics Of Palladio's Villas: Workshop '98 |
|||
|год=2007 |
|||
|ссылка=http://www.emis.de/journals/NNJ/Wassell.html |
|||
|заглавие=Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture |
|||
|издательство=Nexus Network Journal |
|||
|издание=[[Science (journal)|Science]] |
|||
|accessdate=3 October 2015 |
|||
|том=315 |
|||
}} |
|||
|страницы=1106–1110 |
|||
*{{книга |
|||
|doi=10.1126/science.1135491 |
|||
|автор=Andrea Palladio |
|||
|pmid=17322056 |
|||
|ref=Palladio |
|||
|выпуск=5815 |
|||
|заглавие=I quattro libri dell'architettura|author2=Tavernor, Robert; Schofield, Richard (trans.) |
|||
|bibcode=2007Sci...315.1106L |
|||
|издательство=MIT Press |
|||
|год=1997 |
|||
|страницы=book I, chapter xxi |
|||
}} Год изиния оригинала - 1570 |
|||
*{{книга |
|||
|автор= Vincenzo Scamozzi, Vroom W. H. M. (перевод) |
|||
|ref=Scamozzi |
|||
|заглавие=The Idea of a Universal Architecture |
|||
|год=2003 |
|||
|издательство=Architectura & Natura |
|||
}} Год изиния оригинала -1615 |
|||
*{{книга |
|||
|автор=Ann Marie Borys |
|||
|ref=Borys |
|||
|заглавие=Vincenzo Scamozzi and the Chorography of Early Modern Architecture |
|||
|ссылка=https://books.google.com/books?id=ocGMddu1ZeMC&pg=PA140 |
|||
|месяц=March |
|||
|год=2014 |
|||
|издательство=Ashgate Publishing |
|||
|isbn=978-1-4094-5580-6 |
|||
}} |
|||
*{{книга |
|||
|ref=Beckh |
|||
|автор=Matthias Beckh |
|||
|заглавие=Hyperbolic Structures: Shukhov's Lattice Towers - Forerunners of Modern Lightweight Construction |
|||
|ссылка=https://books.google.com/books?id=LpyLBgAAQBAJ&pg=PA75 |
|||
|год=2015 |
|||
|издательство=John Wiley & Sons |
|||
|isbn=978-1-118-93268-1 |
|||
}} |
}} |
||
*{{статья |
*{{статья |
||
|заглавие= |
|заглавие=The Nijni-Novgorod exhibition: Water tower, room under construction, springing of 91 feet span |
||
|издание=The Engineer |
|||
|автор=Dündar A. |
|||
|ref=Nijni-Novgorod exhibition |
|||
|ref=Dündar |
|||
|месяц=March |
|||
|издание=Ankara Üniverstesi İlahiyat Fakültesi Dergisi |
|||
|год=1897 |
|||
|том= 44 |
|||
|страницы=292-294 |
|||
|выпуск=2 |
|||
|место=London |
|||
|страницы=131–172 |
|||
}} |
|||
|год= 2003 |
|||
*{{книга |
|||
|ссылка= http://dergiler.ankara.edu.tr/dergiler/37/727/9212.pdf |
|||
|заглавие=Vladimir G. Suchov 1853—1939. Die Kunst der sparsamen Konstruktion |
|||
|language=tr |
|||
|автор=Rainer |
|||
|ref=Graefe |
|||
|издательство=Deutsche Verlags-Anstalt |
|||
|год=1990 |
|||
|страницы=110–114 |
|||
|isbn=3-421-02984-9 |
|||
}} |
}} |
||
*{{статья |
*{{статья |
||
|автор= |
|автор=Owen Hatherley |
||
|ref= |
|ref=Hatherley |
||
|заглавие=The Constructivists and the Russian Revolution in Art and Architecture |
|||
|издание=Mathematical Intelligencer |
|||
|ссылка=https://www.theguardian.com/artanddesign/2011/nov/04/russian-avant-garde-constructivists |
|||
|том=31 |
|||
|accessdate=6 June 2016 |
|||
|выпуск=1 |
|||
|издание=[[The Guardian]] |
|||
|месяц=November |
|||
|год=2011 |
|||
}} |
|||
*{{статья |
|||
|заглавие=Rietveld Schröderhuis (Rietveld Schröder House) |
|||
|ref=Rietveld Schröderhuis |
|||
|заглавие 2=World Heritage Centre |
|||
|издательство=[[UNESCO]] |
|||
|ссылка=http://whc.unesco.org/en/list/965 |
|||
|accessdate=13 December 2012 |
|||
}} |
|||
*{{книга |
|||
|автор=Laszlo Moholy-Nagy, Daphne M. Hoffman (перевод) |
|||
|ref=Moholy-Nagy |
|||
|заглавие=The New Vision: Fundamentals of Design, Painting, Sculpture, Architecture |
|||
|год=1938 |
|||
|издательство=New Bauhaus Books |
|||
}} |
|||
*{{книга |
|||
|автор=Lynn Gamwell |
|||
|ref=Gamwell |
|||
|заглавие=Mathematics and Art: A Cultural History |
|||
|год=2015 |
|||
|издательство=Princeton University Press |
|||
|isbn=978-0-691-16528-8 |
|||
}} |
|||
*{{книга |
|||
|заглавие=The Modulor: A Harmonious Measure to the Human Scale, Universally Applicable to Architecture and Mechanics |
|||
|автор=Le Corbusier |
|||
|издательство=Birkhäuser |
|||
|год=2004 |
|||
|isbn=3-7643-6188-3 |
|||
}} Год издания оригинала -1954, 1958 |
|||
*{{cite web |
|||
|author=Herb Greene |
|||
|ref=Greene |
|||
|title=Le Corbusier: Notre Dame du Haut at Ronchamp |
|||
|url=http://www.herbgreene.org/WRITING/Le%20CORBUSIER.html |
|||
|accessdate=5 October 2015 |
|||
}} |
|||
*{{книга |
|||
|автор=David A. Hanser |
|||
|ref=Hanser |
|||
|заглавие=Architecture of France |
|||
|ссылка=https://books.google.com/books?id=zojzUU976h0C&pg=PA211 |
|||
|год=2006 |
|||
|издательство=Greenwood Publishing Group |
|||
|isbn=978-0-313-31902-0 |
|||
}} |
|||
*{{статья |
|||
|заглавие=Vanity Fair's World Architecture Survey: the Complete Results |
|||
|ссылка=http://www.vanityfair.com/culture/features/2010/08/architecture-survey-list-201008 |
|||
|accessdate=22 July 2010 |
|||
|newspaper=[[Vanity Fair ]] |
|||
|месяц=June |
|||
|год=2010 |
|||
}} |
|||
*{{статья |
|||
|заглавие=Denver International Airport Press Kit |
|||
|ссылка=https://www.yumpu.com/en/document/view/33421824/denver-international-airport-press-kit-dia-business-center-home- |
|||
|ref=Denver International Airport |
|||
|год=2013 |
|||
|издательство=Fenstress Architects |
|||
}} |
|||
*{{cite web |
|||
|заглавие=Biosphere |
|||
|ref=Biosphere |
|||
|title=http://www.aviewoncities.com/montreal/biosphere.htm |
|||
|website=A view on cities |
|||
|accessdate=1 October 2015 |
|||
}} |
|||
*{{статья |
|||
|автор=Alexander J. Hahn |
|||
|ref=Hahn |
|||
|заглавие=Mathematical Excursions To Architecture |
|||
|ссылка=https://www.insidescience.org/content/mathematical-excursions-architecture/927 |
|||
|издательство=Inside Science |
|||
|accessdate=5 October 2015 |
|||
|месяц=February |
|||
|год=2013 |
|||
}} |
|||
*{{книга |
|||
|заглавие=A Theory of Architecture |
|||
|издательство=Umbau |
|||
|автор=Nikos Salingaros |
|||
|ref=Salingaros |
|||
|год=2006 |
|||
|ссылка=https://books.google.com/books?id=FV_0_RHD4cQC |
|||
}} |
|||
*{{книга |
|||
|ссылка=https://books.google.com/books?id=ezxDPgAACAAJ |
|||
|заглавие=Symphony: Frank Gehry's Walt Disney Concert Hall |
|||
|издательство=Five Ties |
|||
|автор=Frank O. Gehry, Grant Mudford, Richard Koshalek |
|||
|ref=Gehry, Mudford, Koshalek |
|||
|год=2009 |
|год=2009 |
||
|заглавие=The Search for Quasi-Periodicity in Islamic 5-fold Ornament |
|||
|ссылка=http://www.springerlink.com/content/760261153n347478/?p=405b9dbf45ea4f4793a097b6e12dcb08pi=7 |
|||
|doi=10.1007/s00283-008-9018-6 |
|||
}} |
}} |
||
*{{книга |
*{{книга |
||
|ссылка=https://books.google.com/books?id=TrH5I3Ure1EC |
|||
|заглавие=The Mathematics of Egypt, Mesopotamia, China, India, and Islam |
|||
|заглавие=Iron: Erecting the Walt Disney Concert Hall |
|||
|автор=Katz V.J. |
|||
|издательство=Princeton Architectural Press |
|||
|ref=Katz |
|||
|ref=Garcetti |
|||
|страницы= 620 |
|||
|автор=Gil Garcetti |
|||
|издательство= Princeton University Press |
|||
|год=2004 |
|||
}} |
|||
*{{статья |
|||
|ref=Salingaros |
|||
|автор=Nikos Salingaros |
|||
|заглавие=Architecture, Patterns, and Mathematics |
|||
|издание=Nexus Network Journal |
|||
|date=April 1999 |
|||
|том=1 |
|||
|выпуск=2 |
|||
}} |
|||
*{{статья |
|||
|автор=George Markowsky |
|||
|ref=Markowsky |
|||
|ссылка=http://www.math.nus.edu.sg/aslaksen/teaching/maa/markowsky.pdf |
|||
|заглавие=Misconceptions About the Golden Ratio |
|||
|издание=The College Mathematics Journal |
|||
|том=23 |
|||
|выпуск=1 |
|||
|месяц=January |
|||
|год=1992 |
|||
}} |
|||
*{{книга |
|||
|автор=Socrates G. Taseos |
|||
|ref=Taseos |
|||
|заглавие=Back in Time 3104 B.C. to the Great Pyramid |
|||
|издательство=SOC Publishers |
|||
|год=1990 |
|||
}} |
|||
*{{книга |
|||
|автор=Midhat Gazale |
|||
|ref=Gazale |
|||
|заглавие=Gnomon: From Pharaohs to Fractals |
|||
|издательство=Princeton University Press |
|||
|год=1999 |
|||
}} |
|||
*{{книга |
|||
|ref=Cooke |
|||
|автор=Roger L. Cooke |
|||
|заглавие=The History of Mathematics: A Brief Course |
|||
|ссылка=https://books.google.com/books?id=wOGh7XPowAMC |
|||
|издание=2nd |
|||
|год=2011 |
|||
|издательство=John Wiley & Sons |
|||
|isbn=978-1-118-03024-0 |
|||
}} |
|||
*{{книга |
|||
|ref=Gillings |
|||
|автор=Richard J. Gillings |
|||
|заглавие=Mathematics in the Time of the Pharaohs |
|||
|издательство=Dover |
|||
|год=1982 |
|||
}} |
|||
*{{книга |
|||
|ref=Kramrisch |
|||
|автор=Stella Kramrisch |
|||
|год=1976 |
|||
|издательство=The Hindu Temple |
|||
|том=1 & 2 |
|||
|isbn=81-208-0223-3 |
|||
}} |
|||
*{{книга |
|||
|автор=Vibhuti Sachdev, Giles Tillotson |
|||
|ref=Sachdev, Tillotson |
|||
|заглавие=Building Jaipur: The Making of an Indian City |
|||
|год=2004 |
|||
|isbn=978-1-86189-137-2 |
|||
}} |
|||
*{{книга |
|||
|заглавие=A Universal History of Numbers |
|||
|издательство=Penguin |
|||
|ref=Ifrah |
|||
|автор=Georges Ifrah |
|||
|год=1998 |
|||
}} |
|||
*{{статья |
|||
|заглавие=Fractals in Indian Architecture |
|||
|ref=Fractals in Indian Architecture |
|||
|ссылка=https://classes.yale.edu/fractals/Panorama/Architecture/IndianArch/IndianArch.html |
|||
|издательство=Yale University |
|||
|accessdate=1 October 2015 |
|||
}} |
|||
*{{статья |
|||
|ref=Jackson |
|||
|автор=William J. Jackson |
|||
|заглавие=For All Fractal Purposes ... an introduction |
|||
|ссылка=http://liberalarts.iupui.edu/rel/OLD_SITE/Fractals/COVERPAGE.HTM |
|||
|издательство=Indiana University-Purdue University Indianapolis |
|||
|accessdate=1 October 2015 |
|||
|archiveurl=https://web.archive.org/web/20150914170816/http://liberalarts.iupui.edu/rel/OLD_SITE/Fractals/COVERPAGE.HTM |
|||
|archivedate=14 September 2015 |
|||
}} |
|||
*{{книга |
|||
|ref=King |
|||
|автор=Anthony D. King |
|||
|заглавие=Buildings and Society: Essays on the Social Development of the Built Environment |
|||
|год=2005 |
|||
|издательство=Taylor & Francis |
|||
|isbn=0-203-48075-9 |
|||
|ссылка=https://books.google.com/books?id=1HtVU6D2LOUC&printsec=frontcover&dq=Buildings+and+Society:+Essays+on+the+Social+Development+of+the+Built+Environment&hl=en&sa=X&ei=cB7tT6rlBof-8ATw1-yWDQ&ved=0CDYQ6AEwAA#v=onepage&q=meenakshi&f=false |
|||
|page=72 |
|||
}} |
|||
*{{статья |
|||
|автор=O'Connor J. J., Robertson E. F. |
|||
|ref=O'Connor, Robertson |
|||
|заглавие=Mathematics and Architecture |
|||
|ссылка=http://www-history.mcs.st-and.ac.uk/HistTopics/Architecture.html |
|||
|издательство=University of St Andrews |
|||
|accessdate=4 October 2015 |
|||
|месяц=February |
|||
|год=2002 |
|||
}} |
|||
*{{книга |
|||
|автор=Eli Maor |
|||
|ref=Maor |
|||
|заглавие=The Pythagorean Theorem: A 4,000-year History |
|||
|ссылка=https://books.google.com/books?id=Z5VoBGy3AoAC&pg=PA19 |
|||
|год=2007 |
|год=2007 |
||
|издательство=Princeton University Press |
|||
|isbn= 978-0-691-11485-9 |
|||
|isbn=0-691-12526-0 |
|||
|ссылка=https://books.google.com/books?id=3ullzl036UEC&pg=PA620 |
|||
}} |
}} |
||
*{{книга |
|||
*{{статья |
|||
|ref=Norwich |
|||
|заглавие=Pattern, Cognition and contemplation: Exploring the Geometric Art of Iran |
|||
|автор= |
|автор=John Julius Norwich |
||
|заглавие=Great Architecture of the World |
|||
|ref=Henry |
|||
|издательство=Artists House |
|||
|год=2001 |
|||
}} |
|||
*{{книга |
|||
|автор=Francis Penrose |
|||
|ref=Penrose |
|||
|заглавие=Principles of Athenian Architecture |
|||
|издательство=Society of Dilettanti |
|||
|год=1973 |
|||
}} Год оригинального издания =1851 |
|||
*{{статья |
|||
|ref=Stevens |
|||
|автор=Gorham P. Stevens |
|||
|заглавие=Concerning the Impressiveness of the Parthenon |
|||
|издание=American Journal of Archaeology |
|||
|том=66 |
|||
|выпуск=3 |
|||
|месяц=July |
|||
|год=1962 |
|||
|страницы=337–338 |
|||
|doi=10.2307/501468 |
|||
}} |
|||
*{{cite web |
|||
|author=Archibald R. C. |
|||
|ref=Archibald |
|||
|url=http://www.spirasolaris.ca/hambidge1a.html |
|||
|title=Notes on the Logarithmic Spiral, Golden Section and the Fibonacci Series |
|||
|accessdate=1 October 2015 |
|||
}} |
|||
*{{статья |
|||
|ref=Markowsky |
|||
|автор=George Markowsky |
|||
|ссылка=http://www.math.nus.edu.sg/aslaksen/teaching/maa/markowsky.pdf |
|||
|заглавие=Misconceptions about the Golden Ratio |
|||
|издание=The College Mathematics Journal |
|||
|том=23 |
|||
|выпуск=1 |
|||
|месяц=January |
|||
|год=1992 |
|||
}} |
|||
*{{статья |
|||
|ref=Gedal |
|||
|автор=Najib Gedal |
|||
|заглавие=The Great Mosque of Cordoba: Geometric Analysis |
|||
|ссылка=http://islamic-arts.org/2011/the-great-mosque-of-cordoba-geometric-analysis/ |
|||
|издательство=Islamic Art & Architecture |
|||
|accessdate=16 October 2015 |
|||
|год=2011 |
|||
}} |
|||
*{{статья |
|||
|ref=Tennant |
|||
|автор=Raymond Tennant |
|||
|заглавие=International Joint Conference of ISAMA, the International Society of the Arts, Mathematics, and Architecture, and BRIDGES. Mathematical Connections in Art Music, and Science, University of Granada, Spain, July, 2003. Islamic Constructions: The Geometry Needed by Craftsmen. |
|||
|издание=International Joint Conference of ISAMA, the International Society of the Arts, Mathematics, and Architecture, and BRIDGES, Mathematical Connections in Art Music, and Science |
|||
|месяц=July |
|||
|год=2003 |
|||
|ссылка=http://www2.kenyon.edu/Depts/Math/Aydin/Teach/Fall13/128/GeometryNeededbyCraftsmen.pdf |
|||
}} |
|||
*{{книга |
|||
|ref=Irwin |
|||
|автор=Robert Irwin |
|||
|заглавие=The Alhambra |
|||
|ссылка=https://books.google.com/books?id=dS_cIXaGKI4C&pg=PA109 |
|||
|месяц=May |
|||
|год=2011 |
|||
|издательство=Profile Books |
|||
|isbn=1-84765-098-8 |
|||
}} |
|||
*{{статья |
|||
|ref=Robertson |
|||
|автор=Ann Robertson |
|||
|заглавие=Revisiting the Geometry of the Sala de Dos Hermanas |
|||
|ссылка=http://archive.bridgesmathart.org/2007/bridges2007-303.pdf|издательство=BRIDGES |
|||
|accessdate=11 October 2015 |
|||
|год=2007 |
|год=2007 |
||
|издательство=Iran Society |
|||
|ссылка=http://www.iransociety.org/docs/journal_2007.pdf | accessdate=2012-02-08 |
|||
}} |
}} |
||
*{{книга |
|||
*{{статья |
|||
|заглавие=The Art and Architecture of Islam 1250-1800 |
|||
|автор=Marcus Milwright |
|||
|ссылка=https://books.google.com/books?id=-mhIgewDtNkC&pg=PA226 |
|||
|ref=Milwright |
|||
|издательство=Yale University Press |
|||
|заглавие=Gereh Sazi |
|||
|год=1995 |
|||
|издание=Encyclopaedia Iranica Online |
|||
|isbn=0-300-06465-9 |
|||
|accessdate=2013-01-01 |
|||
|автор=Sheila Blair, Jonathan M. Bloom |
|||
|ссылка=http://www.iranicaonline.org/articles/gereh-sazi |
|||
|ref=Blair, Bloom |
|||
}} |
|||
*{{статья |
|||
|ref=Rai |
|||
|автор=Jaswant Rai |
|||
|заглавие=Mathematics and Aesthetics in Islamic Architecture: Reference to Fatehpur Sikri |
|||
|издание=Journal of King Saud University, Architecture & Planning |
|||
|том=5 |
|||
|выпуск=1 |
|||
|год=1993 |
|||
|ссылка=http://repository.ksu.edu.sa/jspui/handle/123456789/560 |
|||
}} |
|||
*{{книга |
|||
|автор=George Michell, Amit Pasricha |
|||
|ref=Michell, Pasricha |
|||
|заглавие=Mughal Architecture & Gardens |
|||
|год=2011 |
|||
|издательство=Antique Collectors Club |
|||
|isbn=978-1-85149-670-9 |
|||
}} |
|||
*{{книга |
|||
|ref=Parker |
|||
|автор=Philip Parker |
|||
|заглавие=World History |
|||
|ссылка=https://books.google.com/books?id=uAUkCOFGgDoC&pg=PA224 |
|||
|год=2010 |
|||
|издательство=Dorling Kindersley |
|||
|isbn=978-1-4053-4124-0 |
|||
}} |
|||
*{{книга |
|||
|ref=Koch |
|||
|автор=Ebba Koch |
|||
|заглавие=The Complete Taj Mahal: And the Riverfront Gardens of Agra |
|||
|edition=1st |
|||
|издательство=Thames & Hudson |
|||
|isbn=0-500-34209-1 |
|||
|страницы=24 and passim |
|||
|год=2006 |
|||
}} |
|||
*{{книга |
|||
|ref=Koch |
|||
|автор=Ebba Koch |
|||
|заглавие=The Complete Taj Mahal: And the Riverfront Gardens of Agra |
|||
|edition=1st |
|||
|издательство=Thames & Hudson |
|||
|isbn=0-500-34209-1 |
|||
|год=2006 |
|||
}} |
|||
*{{книга |
|||
|автор=Michael Fazio, Marian Moffett, Lawrence Wodehouse |
|||
|ref=Fazio, Moffett, Wodehouse |
|||
|заглавие=Buildings Across Time |
|||
|edition=3rd |
|||
|isbn=978-0-07-305304-2 |
|||
|издательство=McGraw-Hill Higher Education |
|||
|год=2009 |
|||
}} |
|||
*{{книга |
|||
|ref=Gamwell |
|||
|автор=Lynn Gamwell |
|||
|заглавие=Mathematics and Art: A Cultural History |
|||
|год=2015 |
|||
|издательство=Princeton University Press |
|||
|isbn=978-0-691-16528-8 |
|||
}} |
|||
*{{книга |
|||
|автор=Fred S. Kleiner, Christin J. Mamiya |
|||
|ref=Kleiner, Mamiya |
|||
|заглавие=[[Gardner's Art Through the Ages (книга)|Gardner's Art Through the Ages: Volume I, Chapters 1–18]] |
|||
|издательство=Wadsworth |
|||
|edition=12th |
|||
|год=2008 |
|||
|isbn=0-495-46740-5 |
|||
}} |
|||
*{{статья |
|||
|автор=Hanna Menander, Olof Brandt, Agostina Appetechia, Håkan Thorén |
|||
|ref=Menander, Brandt, Appetechia, Thorén |
|||
|заглавие=The Lateran Baptistery in Three Dimensions |
|||
|ссылка=http://samla.raa.se/xmlui/bitstream/handle/raa/5009/ro2010_18.pdf |
|||
|издательство=Swedish National Heritage Board |
|||
|accessdate=30 October 2015 |
|||
|год=2010 |
|||
}} |
|||
*{{cite web |
|||
|title=The Baptistery |
|||
|ref=Baptistery |
|||
|ссылка=http://www.leaningtowerofpisa.net/pisa-baptistery.html |
|||
|website=The Leaning Tower of Pisa |
|||
|accessdate=30 October 2015 |
|||
}} |
|||
*{{cite web |
|||
|ref=Huyser-Konig |
|||
|author=Joan Huyser-Konig |
|||
|title=Theological Reasons for Baptistry Shapes |
|||
|url=http://worship.calvin.edu/resources/resource-library/theological-reasons-for-baptistry-shapes/ |
|||
|publisher=Calvin Institute of Christian Worship |
|||
|accessdate=30 October 2015 |
|||
}} |
|||
*{{книга |
|||
|ref=Kuehn |
|||
|автор=Regina Kuehn |
|||
|заглавие=A Place for Baptism |
|||
|ссылка=https://books.google.com/books?id=Sf2hmbe1J30C&pg=PA53 |
|||
|год=1992 |
|||
|издательство=Liturgy Training Publications |
|||
|isbn=978-0-929650-00-5 |
|||
|страницы=53–60 |
|||
}} |
|||
*{{книга |
|||
|автор=Augustine of Hippo |
|||
|ref=Augustine of Hippo |
|||
|заглавие=The City of God |
|||
|год=426 |
|||
|страницы=Book 22, Chapter 30 |
|||
}} |
|||
*{{книга |
|||
|ref=Kleiner |
|||
|автор=Fred Kleiner |
|||
|заглавие=Gardner's Art through the Ages: A Global History |
|||
|ссылка=https://books.google.com/books?id=PR4KAAAAQBAJ&pg=PT389 |
|||
|год=2012 |
|||
|издательство=Cengage Learning |
|||
|isbn=1-133-71116-2 |
|||
}} |
|||
*{{cite web |
|||
|title=Zelená hora near Žďár nad Sázavou |
|||
|url=http://www.czechtourism.com/c/zdar-nad-sazavou-unesco-zelena-hora-pilgrimage-church-of-st-john-nepomuk/ |
|||
|publisher=Czech Tourism |
|||
|accessdate=10 November 2015 |
|||
}} |
|||
*{{cite web |
|||
|title=Attributes of Saint John of Nepomuk |
|||
|url=http://www.sjn.cz/eng/attributes.htm |
|||
|website=Saint John of Nepomuk |
|||
|accessdate=10 November 2015 |
|||
}} |
|||
*{{статья |
|||
|заглавие=Drawing Together Euclidean and Topological Threads (pdf) |
|||
|автор=Burry M.C., Burry J.R., Dunlop G.M., Maher A. |
|||
|ref=Burry, Burry, Dunlop, Maher |
|||
|часть=Presented at SIRC 2001 – the Thirteenth Annual Colloquium of the Spatial Information Research Center |
|||
|издательство=University of Otago |
|||
|место=Dunedin, New Zealand |
|||
|год=2001 |
|год=2001 |
||
|ссылка=http://www.business.otago.ac.nz/SIRC05/conferences/2001/05_burry.pdf |
|||
|accessdate=2007-11-28 |
|||
|archiveurl=https://web.archive.org/web/20071031134218/http://www.business.otago.ac.nz/SIRC05/conferences/2001/05_burry.pdf |
|||
|archivedate=2007-10-31 |
|||
}} |
}} |
||
*{{статья |
*{{статья |
||
|ref=Freiberger |
|||
|автор=Terry Allen |
|||
|автор=Marianne Freiberger |
|||
|ref=Allen |
|||
|заглавие=Perfect buildings: the maths of modern architecture |
|||
|год=2004 |
|||
|ссылка=https://plus.maths.org/content/perfect-buildings-maths-modern-architecture |
|||
|заглавие=Islamic Art and the Argument from Academic Geometry |
|||
|издательство=Plus magazine |
|||
|ссылка=http://sonic.net/~tallen/palmtree/academicgeometry.htm |
|||
|accessdate= |
|accessdate=5 October 2015 |
||
|месяц=March |
|||
|год=2007 |
|||
}} |
|||
*{{книга |
|||
|автор=Andrea Simitch, Val Warke |
|||
|ref=Simitch, Warke |
|||
|заглавие=The Language of Architecture: 26 Principles Every Architect Should Know |
|||
|ссылка=https://books.google.com/books?id=2v-1AwAAQBAJ&pg=PT191 |
|||
|год=2014 |
|||
|издательство=Rockport Publishers |
|||
|isbn=978-1-62788-048-0 |
|||
}} |
|||
*{{cite web |
|||
|title=The Geometry of Antoni Gaudi |
|||
|url=http://euler.slu.edu/escher/index.php/The_Geometry_of_Antoni_Gaudi|website=Math & the Art of MC Escher |
|||
|publisher=Saint Louis University Mathematics and Computer Science |
|||
|accessdate=4 October 2015 |
|||
}} |
}} |
||
*{{статья |
*{{статья |
||
|ref=Usvat |
|||
|заглавие=Materials and Mediums |
|||
|автор=Liliana Usvat |
|||
|издание=Pattern in Islamic Art |
|||
|заглавие=Antony Gaudi and Mathematics |
|||
|accessdate = 2012-02-08 |
|||
|ссылка=http://www.mathematicsmagazine.com/Articles/AntonyGaudiandMathematics.php#.VhFZ7WtUWHg |
|||
|автор=David Wade |
|||
|издательство=Mathematics Magazine |
|||
|ref=March |
|||
|accessdate=4 October 2015 |
|||
|year=2006 |
|||
}} |
|||
|ссылка=http://www.patterninislamicart.com/background-notes/materials-and-mediums/ |
|||
*{{статья |
|||
|автор=Burry M.C., Burry J.R., Dunlop G.M., Maher A. |
|||
|ref=Burry, Burry, Dunlop, Maher |
|||
|заглавие=Drawing Together Euclidean and Topological Threads |
|||
|ссылка=http://www.business.otago.ac.nz/SIRC05/conferences/2001/05_burry.pdf |
|||
|год=2001 |
|||
|издательство=The 13th Annual Colloquium of the Spatial Information Research Centre, University of Otago, Dunedin, New Zealand |
|||
|accessdate=5 August 2008 |
|||
|archiveurl=https://web.archive.org/web/20080625010337/http://www.business.otago.ac.nz/SIRC05/conferences/2001/05_burry.pdf|archivedate=25 June 2008 |
|||
}} |
}} |
||
*{{cite web |
*{{cite web |
||
|ref=Nervi |
|||
|author=G. Lekegian |
|||
|author=Pier Luigi Nervi |
|||
|ref=Lekegian |
|||
|title=Cathedral of Saint Mary of the Assumption |
|||
|title=Jami' Ibn Tulun |
|||
|url=http://architectuul.com/architecture/cathedral-of-saint-mary-of-the-assumption |
|||
|url=http://archnet.org/sites/1522/media_contents/6256 |
|||
|website=Architectuul |
|||
|accessdate=25 January 2017 |
|||
|accessdate=12 October 2015 |
|||
|year=2017 |
|||
}} |
|||
*{{cite web |
|||
|url=http://www.aboutbrasilia.com/travel/brasilia-cathedral.html |
|||
|title=Brasilia Cathedral |
|||
|publisher=About Brasilia |
|||
|accessdate=13 November 2015 |
|||
}} |
|||
*{{книга |
|||
|автор=Ehrhard Behrends, Nuno Crato, Jose Francisco Rodrigues |
|||
|ref=Behrends, Crato, Rodrigues |
|||
|заглавие=Raising Public Awareness of Mathematics |
|||
|ссылка=https://books.google.com/books?id=b3aIukYk6ccC&pg=PA143 |
|||
|год=2012 |
|||
|издательство=Springer Science & Business Media |
|||
|isbn=978-3-642-25710-0 |
|||
}} |
|||
*{{книга |
|||
|ref=Emmer |
|||
|автор=Michele Emmer |
|||
|заглавие=Imagine Math: Between Culture and Mathematics |
|||
|ссылка=https://books.google.com/books?id=qcaeLynFUzgC&pg=PA111 |
|||
|год=2012 |
|||
|издательство=Springer Science & Business Media |
|||
|isbn=978-88-470-2427-4 |
|||
}} |
}} |
||
*{{статья |
*{{статья |
||
|ref=Mkrtchyan |
|||
|заглавие=Architecture – iv. Central Asian |
|||
|автор=Ruzanna Mkrtchyan |
|||
|издание=Encyclopaedia Iranica |
|||
|заглавие=Cathedral of Brasilia |
|||
|ссылка=http://www.iranicaonline.org/articles/architecture-iv |
|||
|ссылка=http://www.building.am/page.php?id=149 |
|||
|accessdate=2012-02-08 |
|||
|издательство=Building.AM |
|||
|год=1986 |
|||
|accessdate=13 November 2015 |
|||
|автор=Pugachenkova G. A. |
|||
|год=2013 |
|||
|ref=Pugachenkova |
|||
}} |
|||
*{{cite web |
|||
|url=http://www.nordenskirker.dk/Tidligere/oesterlars_kirke/oesterlars_kirke.htm |
|||
|title=Østerlars kirke |
|||
|publisher=Nordens kirker |
|||
|language=Danish |
|||
|accessdate=2 December 2016 |
|||
}} |
|||
*{{cite web |
|||
|url=http://www.naturbornholm.dk/default.asp?m=373 |
|||
|title=Østerlars kirke |
|||
|publisher=Natur Bornholm |
|||
|language=Danish |
|||
|accessdate=2 December 2016 |
|||
}} |
|||
{{статья |
|||
|url= http://socialsciences.exeter.ac.uk/education/research/centres/stem/publications/pmej/pome24/ronning%20_geometry_and_Islamic_patterns.pdf |
|||
|заглавие=Islamic Patterns And Symmetry Groups |
|||
|издательство=University of Exeter |
|||
|accessdate=18 April 2014 |
|||
|автор= Frode Rønning, |
|||
|ref=Rønning |
|||
|год=2009 |
|||
}} |
|||
*{{статья |
|||
|автор=Matt Gibberd, Albert Hill |
|||
|ref=Gibberd, Hill |
|||
|заглавие=The Return of Ornamentation |
|||
|ссылка=http://www.telegraph.co.uk/luxury/property-and-architecture/7279/the-return-of-ornamentation.html |
|||
|accessdate=12 October 2015 |
|||
|издание=The Telegraph |
|||
|месяц=August |
|||
|год=2013 |
|||
}} |
|||
*{{статья |
|||
|заглавие=Ravensbourne College by Foreign Office Architects |
|||
|ссылка=http://www.dezeen.com/2010/09/13/ravensbourne-college-by-foreign-office-architects/ |
|||
|издательство=de zeen magazine |
|||
|accessdate=12 October 2015 |
|||
|месяц=September |
|||
|год=2010 |
|||
}} |
|||
*{{cite web |
|||
|last1=Bizley|first1=Graham |
|||
|title=FOA's peninsula patterns for Ravensbourne College |
|||
|url=http://www.bdonline.co.uk/foa%E2%80%99s-peninsula-patterns-for-ravensbourne-college/3144928.article|website=bdonline.co.uk |
|||
|accessdate=16 October 2015 |
|||
}} |
}} |
||
*{{книга |
*{{книга |
||
|автор=Duffy C. |
|||
|часть= Urban development and architecture |
|||
|ref=Duffy |
|||
|автор=Pugachenkova G. A., Dani A. H., Liu Yingsheng |
|||
|год=1975 |
|||
|ref=Pugachenkova, Dani, Yingsheng |
|||
|заглавие=Fire & Stone, The Science of Fortress Warfare 1660–1860 |
|||
|заглавие=History of Civilizations of Central Asia. The Age of Achievement: A.D. 750 to the End of the Fifteenth Century – Part Two: The Achievements |
|||
|издательство=Booksales |
|||
|isbn=978-92-3-103654-5 |
|||
|isbn=978-0-7858-2109-0 |
|||
|ссылка=http://unesco.culture.free.fr/asia-new/html_eng/chapitre4218/chapitre1.htm |
|||
|издательство=unesco |
|||
|том=IV |
|||
|год=2000 |
|||
}} |
}} |
||
*{{книга |
|||
|ref=Chandler |
|||
|автор=David Chandler |
|||
|заглавие=The Art of Warfare in the Age of Marlborough |
|||
|год=1990 |
|||
|издательство=Spellmount |
|||
|isbn=978-0-946771-42-4 |
|||
}} |
|||
*{{книга |
|||
|автор=Siegfried Giedion |
|||
|ref=Giedion |
|||
|заглавие=Space, Time and Architecture |
|||
|издательство=Harvard University Press |
|||
|год=1962 |
|||
}} Год издания оригинальной статьи - 1941 |
|||
*{{статья |
*{{статья |
||
|ref=O'Neill |
|||
|автор=Emil Makovicky |
|||
|автор=Tom O'Neill |
|||
|ref=Makovicky |
|||
|заглавие= |
|заглавие=China's Remote Fortresses Lose Residents, Gain Tourists |
||
|ссылка=http://news.nationalgeographic.com/news/2015/01/150102-hakka-china-tulou-fujian-world-heritage-culture-housing/ |
|||
|ссылка=http://www.sciencemag.org/content/318/5855/1383.1.full |
|||
|издательство=[[National Geographic (журнал)|National Geographic]] |
|||
|accessdate=2012-02-22 |
|||
|accessdate=6 January 2017 |
|||
|год=2007 |
|||
|месяц=January |
|||
|издание=Science |
|||
|год=2015 |
|||
|том=318 |
|||
}} |
|||
|выпуск=5855 |
|||
* {{статья |
|||
|DOI=10.1126/science.1146262 |
|||
|автор= Mahdavinejad M., Kavan Javanrudi |
|||
|ref=Mahdavinejad, Javanrudi |
|||
|заглавие=Assessment of Ancient Fridges: A Sustainable Method to Storage Ice in Hot-Arid Climates |
|||
|издание=Asian Culture and History |
|||
|месяц=July |
|||
|год=2012 |
|||
|том=4 |
|||
|выпуск=2 |
|||
|doi=10.5539/ach.v4n2p133 |
|||
}} |
}} |
||
{{refend}} |
{{refend}} |
||
==Ссылки== |
|||
* [http://www.nexusjournal.com Nexus Network Journal: Architecture and Mathematics Online] |
|||
{{Исламская архитектура }} |
|||
* [http://www.isama.org The International Society of the Arts, Mathematics, and Architecture] |
|||
{{Исламское искусство}} |
|||
* [http://www-gap.dcs.st-and.ac.uk/~history/HistTopics/Architecture.html University of St Andrews: Mathematics and Architecture] |
|||
{{Орнаменты}} |
|||
* [http://www.math.nus.edu.sg/aslaksen/teaching/math-art-arch.shtml National University of Singapore: Mathematics in Art and Architecture] |
|||
* [http://www.dartmouth.edu/~matc/math5.geometry/unit1/INTRO.html Dartmouth College: Geometry in Art & Architecture] |
|||
Версия от 22:00, 29 октября 2017


Математика и архитектура' are related, since, as with other arts, архитекторы use математика for several reasons. Apart from the Математика needed when engineering здания, архитекторы use геометрию: to define the spatial form of a building; from the Pythagoreans of the sixth century BC onwards, to create forms considered harmonious, and thus to lay out buildings and their surroundings according to mathematical, aesthetic and sometimes religious principles; to decorate buildings with mathematical objects such as замощений; and to meet environmental goals, such as to minimise wind speeds around the bases of tall buildings.
In Древнем Египте, Ancient Greece, Индии, and the Islamic world, buildings including pyramids, temples, мечети, palaces and мавзолеи were laid out with specific proportions for religious reasons. В исламской архитектуре geometric shapes and геометрические мозаичные орнаменты[англ.] are used to decorate buildings, both inside and outside. Some Hindu temples have a Фрактал-like structure where parts resemble the whole, conveying a message about the infinite in индуистской космологии. In архитектуре Китая, the тулоу of провинции Фуцзянь are circular, communal defensive structures. In the twenty-first century, mathematical ornamentation is again being used to cover public buildings.
In Renaissance architecture, Симметрия and proportion were deliberately emphasized by архитекторами such as Leon Battista Alberti, Sebastiano Serlio and Andrea Palladio, influenced by Vitruvius's De architectura from Ancient Rome и арифметика of the Pythagoreans from Ancient Greece. At the end of the nineteenth century, Vladimir Shukhov in Russia and Antoni Gaudí in Барселона pioneered the use of Гиперболоидные конструкции; in the Саграда-Фамилия, Gaudí also incorporated hyperbolic Параболоидs, tessellations, Арка с очертанием обратной цепной линии[англ.]es, Катеноидs, Геликоидs, and ruled surfaces. In the twentieth century, styles such as Архитектурный модернизм and Деконструктивизм explored different geometries to achieve desired effects. Minimal surfaces have been exploited in tent-like roof coverings as at Denver International Airport, while Richard Buckminster Fuller pioneered the use of the strong thin-shell structures known as geodesic domes.
Connected fields

Архитекторы Michael Ostwald and Kim Williams, considering the relationships between архитектурой и математикой, note that the fields as commonly understood might seem to be only weakly connected, since Архитектура is a profession concerned with the practical matter of making buildings, while Математика is the pure study of number and other abstract objects. But, they argue, the two are strongly connected, and have been since antiquity. In Древнем Риме, Витрувий described an архитектору as a man who knew enough of a range of other disciplines, primarily Геометрия, to enable him to oversee skilled artisans in all the other necessary areas, such as masons and carpenters. The same applied in the Средние века, where graduates learnt арифметику, геометрию and эстетику alongside the basic syllabus of grammar, logic, and rhetoric (тривиум) in elegant halls made by master builders who had guided many craftsmen. A master builder at the top of his profession was given the title of архитектора or engineer. In the Возрождения, квадривиум of арифметика, геометрия, music and astronomy became an extra syllabus expected of the человек эпохи Возрождения such as Leon Battista Alberti. Similarly in England, Sir Christopher Wren, known today as архитектор, was firstly a noted astronomer[3].
Williams and Ostwald, further overviewing the interaction of математики and Архитектура since 1500 according to the approach of the German sociologist Theodor W. Adorno|Theodor Adorno, identify three tendencies among архитекторов, namely: to be revolutionary, introducing wholly new ideas; реакционеры, failing to introduce change; or Художники возрождения[англ.], actually going backwards. They argue that архитекторы have avoided looking to Математика for inspiration in revivalist times. This would explain why in revivalist periods, such as the Неоготика in 19th century England, Архитектура had little connection to математикой. Equally, they note that in reactionary times such as the Italian Маньеризм of about 1520 to 1580, or the 17th century барокко and Палладианство movements, Математика was barely consulted. In contrast, революционные early 20th century movements such as футуризм and конструктивизм[англ.]* actively rejected old ideas, embracing Математика and leading to Модернизм Архитектура. Towards the end of the 20th century, too, fractal геометрияwas quickly seized upon by архитекторами, as was Непериодичное замощение[англ.], to provide interesting and attractive coverings for buildings[4].
Архитекторы используют математику for several reasons, leaving aside the necessary use of математики in the проектировании зданий[англ.][5]. Firstly, they use геометрию because it defines the spatial form of a building[6]. Secondly, they use математику to design forms that are considered beautiful or harmonious[7]. From the time of the Pythagoreans with their religious philosophy of number[8], архитекторы in Ancient Greece, Древний Рим, the Islamic world and the Italian Renaissance have chosen the proportions of the built environment – buildings and their designed surroundings – according to mathematical as well as эстетика and sometimes religious principles[9][10][11][12]. Thirdly, they may use mathematical objects such as tessellations to decorate buildings[13][14]. Fourthly, they may use математику in the form of computer modelling to meet environmental goals, such as to minimise whirling air currents at the base of tall buildings[1].
Harmonious spatial forms
Secular эстетика
Древний Рим
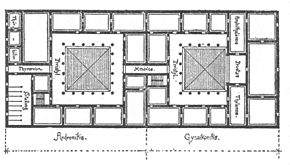
Витрувий

The influential Ancient Roman архитектор Витрувий argued that the design of a building such as a temple depends on two qualities, proportion and symmetria. Proportion ensures that each part of a building relates harmoniously to every other part. Symmetria in Витрувий's usage means something closer to the English term modularity than mirror symmetry, as again it relates to the assembling of (modular) parts into the whole building. In his базилике at Fano, he uses ratios of small integers, especially the triangular numbers (1, 3, 6, 10, ...) to proportion the structure into (виртувиановы) модули[англ.].[a] Thus Базилика's width to length is 1:2; the aisle around it is as high as it is wide, 1:1; the columns are five feet thick and fifty feet high, 1:10[9].

Витрувий named three qualities required of Архитектура in his De architectura, c. 15 B.C.: firmness, usefulness (or «Commodity» in Henry Wotton's 16th century English), and delight. These can be used as categories for classifying the ways in which математика is used in архитектуре. Firmness encompasses the use of математики to ensure a building stands up, hence the mathematical tools used in design and to support construction, for instance to ensure stability and to model performance. Usefulness derives in part from the effective application of математики, reasoning about and analysing the spatial and other relationships in a design. Delight is an attribute of the resulting building, resulting from the embodying of mathematical relationships in the building; it includes эстетику, sensual and intellectual qualities[16].
The Pantheon
Пантеон в Риме has survived intact, illustrating classical Roman structure, proportion, and decoration. The main structure is a dome, the apex left open as a circular oculus to let in light; it is fronted by a short colonnade with a triangular pediment. The height to the окулюс and the diameter of the interior circle are the same, 43,3 метра (140 фута), so the whole interior would fit exactly within a cube, and the interior could house a sphere of the same diameter[17]. These dimensions make more sense when expressed in списке древнеримских единиц: The dome spans 150 римских футов[англ.]*[b]); Окулюс is 30 Roman feet in diameter; the doorway is 40 Roman feet high[18]. The Pantheon remains the world's largest unreinforced concrete dome[19].
Возрождение

Первым трактатом эпохи возрождения по архитектуре был трактат Леона Баттиста Альберти (1450) On the Art of Building[англ.] (Об искусстве строительства). Трактат стал первой печатной книгой по архитектуре в 1485. Трактат частично базировался на книге Витрувия Десять книг об архитектуре и, через Никомах, пифагоровой арифметике. Альберти начинает с куба и выводит из него пропорции. Так, диагонали грани дают отношение 1:√2, а диаметр сферы, описаннвй вокруг куба имеет отношение 1:√3[20][21]. Альберто также описывает открытие Филиппо Брунеллески линейной перспективы[англ.], разработанной для планирования зданий, которые выглядят вполне пропорционально, если рассматривать с удобного расстояния[12].

Следующим важным текстом была книга Себастьяна Серлио Regole generali d'architettura (Основные правила архитектуры). Первый том книги вышел в Венеции в 1537. Том 1545-го года (книги 1 и 2) охватывают геометрию и перспективу[англ.]. Два метода Серлио построения перспективы были ошибочными, но это не остановило широкое использование книги[23].

В 1570 Андреа Палладио опубликовал авторитетные I quattro libri dell'architettura (Четыре книги об архитектуре) в Венеции. Эти книги получили широкое распространение и распространяли идеи итальянского возрождения на остальную Европу в содействии со сторонниками идей, такими как английский дипломат Генри Уоттон, выпустивший в 1624 Элементы архитектуры[24]. Пропорции каждого помещения внутри особняка вычислялись с помощью простых математических отношений, таких как 3:4 и 4:5, и различные помещения внутри дома были связаны этими соотношениями. Ранние архитекторы использовали эти формулы для балансирования симметрии фасада. Однако, проекты Палладио относились, как правило, к квадратным особнякам[25]. Палладио допускал ряд отношений в Quattro libri, утверждая[26][27]:
Имеется семь типов помещений, наиболее прекрасных и хорошо пропорциональных. Это круглые, хотя они редки, квадратные или их длина равна диагонали квадрата ширины, ширине с третью, ширине с половиной, ширине и две трети и две ширины.[c]
In 1615, Vincenzo Scamozzi published the late Возрождение treatise L'Idea dell'Architettura Universale (The Idea of a Universal Архитектуры)[28]. He attempted to relate the design of cities and buildings to the ideas Витрувия and the Pythagoreans, and to the more recent ideas of Palladio[29].
Девятнадцатый век

Гиперболоидные конструкции were used starting towards the end of the nineteenth century by Vladimir Shukhov for masts, lighthouses and cooling towers. Their striking shape is both эстетический interesting and strong, using structural materials economically. Shukhov's first hyperboloidal tower was exhibited in Нижнем Новгороде в 1896[30][31][32].
Двадцатый век

The early twentieth century movement Modern Architecture, pioneered{{efn|Constructivism influenced Bauhaus and Ле Корбюзье, for example[33] by Russian Constructivism[33], used rectilinear Euclidean (also called декартовыми) Геометрия. In the Де Стейл movement, the horizontal and the vertical were seen as constituting the universal. Архитектурные form consists of putting these two directional tendencies together, using roof planes, wall planes and balconies, which either slide past or intersect each other, as in the 1924 Дом Шрёдер by Gerrit Rietveld[34].

Архитекторы модернизма were free to make use of curves as well as planes. Charles Holden's 1933 станция лондонской подземки в Арнос Гроув[англ.] has a circular ticket hall in brick with a flat concrete roof.[35] In 1938, the Bauhaus painter Laszlo Moholy-Nagy adopted Рауля Генриха Франсе[англ.] seven biotechnical elements, namely the crystal, the sphere, the cone, the plane, the (cuboidal) strip, the (cylindrical) rod, and the spiral, as the supposed basic building blocks of Архитекторы inspired by nature[36][37].
Le Corbusier proposed an anthropometric масштаб of proportions in архитектуре, модулор (система пропорций), based on the supposed height of a man[38]. Ле Корбюзье's 1955 Нотр-Дам-дю-О uses free-form curves not describable in mathematical formulae.[d] The shapes are said to be evocative of natural forms such as the нос[англ.]* корабля or praying hands[41]. The design is only at the largest scale: there is no hierarchy of detail at smaller scales, and thus no Фрактал dimension; the same applies to other famous twentieth-century buildings such as the Сиднейский оперный театр, Denver International Airport, and the Музей Гуггенхейма в Бильбао [39].
Aрхитектура 21-го века[англ.], in the opinion of the 90 leading архитекторыwho responded to a 2010 Опрос о мировой архитектуре[англ.], is extremely diverse; the best was judged to be Фрэнк Гери's Музей Гуггенхейма в Бильбао[42].

Здание терминала Международного аэропорта Дэнвера, построенные в 1995, has a тканевую крышу[англ.] supported as a Минимальная поверхность (i.e., its средняя кривизна[англ.]* is zero) by steel cables. It evokes Colorado's snow-capped mountains and the teepee tents of Native Americans (часто их неверно называют вигвамами)[43][44].
Архитектор Richard Buckminster Fuller is famous for designing strong thin-shell structures known as geodesic domes. Биосфера (Монреаль) dome is 61 метр (200 фут) high; its diameter is 76 метров (249 футов)[45].
Сиднейский оперный театр has a dramatic roof consisting of soaring white vaults, reminiscent of ship's sails; to make them possible to construct using standardized components, the vaults are all composed of triangular sections of spherical shells with the same radius. These have the required uniform curvature in every direction[46].
The late twentieth century movement Деконструктивизм creates deliberate disorder with what Nikos Salingaros в книге A Theory of Architecture (Теория архитектуры) calls random forms[47] of high complexity[48] by using non-parallel walls, superimposed grids and complex 2-D surfaces, as in Frank Gehry's Концертный зал имени Уолта Диснея and Музей Гуггенхейма в Бильбао[49][50]. Until the twentieth century, Архитектура students were obliged to have a grounding in математике. Salingaros argues that first «overly simplistic, politically-driven» Модернизм and then «anti-scientific» Деконструктивизм have effectively separated Архитектура from математики. He believes that this «reversal of mathematical values» is harmful, as the «pervasive aesthetic» of non-mathematical Архитектура trains people «to reject mathematical information in the built environment»; he argues that this has negative effects on society[39].
-
Uniform Кривизна: Сиднейский оперный театр, 1973
-
Деконструктивизм: Концертный зал имени Уолта Диснея, Los Angeles, 2003
Religious principles
Древний Египет


The pyramids of Древнего Египта are tombs constructed with deliberately chosen proportions, but which these were has been debated. The face angle is about 51°85’, and the ratio of the slant height to half the base length is 1.619, less than 1% from the золотого сечения. If this was the design method, it would imply the use of треугольника Кеплера (face angle 51°49’)[51][52]. However it is more likely that the pyramids' slope was chosen from the тругольник 3-4-5[англ.] (face angle 53°8’), known from the папируса Ахмеса (c. 1650 – 1550 BC); or from the triangle with base to hypotenuse ratio 1:4/π (face angle 51°50’)[53].
The possible use of the 3-4-5 triangle to lay out right angles, such as for the ground plan of a pyramid, and the knowledge of Pythagoras theorem which that would imply, has been much asserted[54]. It was first conjectured by the historian Moritz Cantor in 1882[54]. It is known that right angles were laid out accurately in древнем Египте[54]; that their surveyors did use верёвку с узлами[англ.]s for measurement[54]; that Плутарх recorded in Об Исиде и Осирисе (around 100 AD) that the Egyptians admired the 3-4-5 triangle[54]; and that the Берлинский папирус 6619[англ.] from the Среднего царства (before 1700 BC) stated that «the area of a square of 100 is equal to that of two smaller squares. The side of one is ½ + ¼ the side of the other.»[55]. The historian of математики Roger L. Cooke observes that «It is hard to imagine anyone being interested in such conditions without knowing the Теорема Пифагора.» [54] Against this, Cooke notes that no Egyptian text before 300 BC actually mentions the use of the theorem to find the length of a triangle's sides, and that there are simpler ways to construct a right angle. Cooke concludes that Cantor's conjecture remains uncertain: he guesses that the древний египтяне probably did know the Теорема Пифагора, but that «there is no evidence that they used it to construct right angles»[54].
Древняя Индия

Vaastu Shastra, the ancient Indian canons of архитектуры and town planning, employs symmetrical drawings called мандалы. Complex calculations are used to arrive at the dimensions of a building and its components. The designs are intended to integrate Архитектура with nature, the relative functions of various parts of the structure, and ancient beliefs utilizing geometric patterns (yantra), Симметрия and направление[англ.] alignments[56]{{sfn|Sachdev, Tillotson|2004|с=155–160}. However, early builders may have come upon mathematical proportions by accident. The mathematician Georges Ifrah notes that simple «tricks» with string and stakes can be used to lay out geometric shapes, such as ellipses and right angles[12][57].
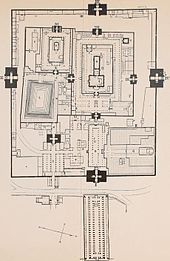
Математика фракталов has been used to show that the reason why existing buildings have universal appeal and are visually satisfying is because they provide the viewer with a sense of scale at different viewing distances. For example, in the tall gopuram gatehouses of Hindu temples such as the Virupaksha Temple at Hampi built in the seventh century, and others such as the храм Кандарья-Махадева at Группа храмов Кхаджурахо[англ.], the parts and the whole have the same character, with фрактальной размерностью in the range 1.7 to 1.8. The cluster of smaller towers (shikhara, lit. 'mountain') about the tallest, central, tower which represents the holy гора Кайлас, abode of божества Шива, depicts the endless repetition of universes in индуистской космологии [2][58] The religious studies scholar William J. Jackson observed of the pattern of towers grouped among smaller towers, themselves grouped among still smaller towers, that:
The ideal form gracefully artificed suggests the infinite rising levels of existence and consciousness, expanding sizes rising toward transcendence above, and at the same time housing the sacred deep within[58]Jackson[59]
Храм Минакши is a large complex with multiple shrines, with the streets of Мадурай laid out concentrically around it according to the shastras. The four gateways are tall towers (gopurams) with Фрактал-like repetitive structure as at Хампи. The enclosures around each shrine are rectangular and surrounded by high stone walls[60].
Ancient Greece

Pythagoras (c. 569 – c. 475 B.C.) and his followers, the Pythagoreans, held that «all things are numbers». They observed the harmonies produced by notes with specific small-integer ratios of frequency, and argued that buildings too should be designed with such ratios. The Greek word symmetria originally denoted the harmony of архитектурных shapes in precise ratios from a building's smallest details right up to its entire design[12].

Парфенон is 69,5 метра (230 фута) long, 30,9 метра (100 фута) wide and 13,7 метра (45 фута) high to the cornice. This gives a ratio of width to length of 4:9, and the same for height to width. Putting these together gives height:width:length of 16:36:81, or to the delight[61] of the Pythagoreans 42:62:92. This sets the module as 0.858 m. A 4:9 rectangle can be constructed as three contiguous rectangles with sides in the ratio 3:4. Each half-rectangle is then a convenient 3:4:5 right triangle, enabling the angles and sides to be checked with a suitably knotted rope. The inner area (naos) similarly has 4:9 proportions (21,44 метра (70 фута) wide by 48.3 m long); the ratio between the diameter of the outer columns, 1,905 метра (6,3 фута), and the spacing of their centres, 4,293 метра (14 фута), is also 4:9[12].
Парфенон is considered by authors such as John Julius Norwich «the most perfect Doric temple ever built»[62]. Its elaborate архитектурных refinements include «a subtle correspondence between the Кривизна of the stylobate, the taper of the naos walls and the энтазис of the columns»[62]. Энтазис refers to the subtle diminution in diameter of the columns as they rise. The stylobate is the platform on which the columns stand. As in other classical Greek temples[63], the platform has a slight parabolic upward Кривизна to shed rainwater and reinforce the building against earthquakes. The columns might therefore be supposed to lean outwards, but they actually lean slightly inwards so that if they carried on, they would meet about a mile above the centre of the building; since they are all the same height, the Кривизна of the outer stylobate edge is transmitted to the Архитрав and roof above: «all follow the rule of being built to delicate curves»[64].
Золотое сечение was known in 300 B.C., when Евклид described the method of geometric construction.[65] It has been argued that the золотое сечение was used in the design of the Парфенон and other ancient Greek buildings, as well as sculptures, paintings, and vases[66]. More recent authors such as Никос Салингарос, however, doubt all these claims.[67] Experiments by the computer scientist George Markowsky failed to find any preference for the Золотой прямоугольник[51].
Исламская архитектура

The historian of Islamic art Antonio Fernandez-Puertas suggests that the Альгамбра, like the Кóрдовская соборная мечеть в Кордове [68], was designed using the Hispano-Muslim foot or codo of about 0,62 метра (2,0 фута). In the palace's львином дворике, the proportions follow a series of радикалов. A rectangle with sides 1 and √2 has (by Pythagoras's theorem) a diagonal of √3, which describes the right triangle made by the sides of the court; the series continues with √4 (giving a 1:2 ratio), √5 and so on. The decorative patterns are similarly proportioned, √2 generating squares inside circles and eight-pointed stars, √3 generating six-pointed stars. There is no evidence to support earlier claims that золотое сечение was used in the Альгамбра[10][69]. [[Львиный дворик ]] is bracketed by the Hall of Two Sisters and the Hall of the Abencerrajes; правильный шестиугольник can be drawn from the centres of these two halls and the four inside corners of the львиного дворика[70].

Мечеть Селимие в городе Эдирне, Турция, was built by Мимаром Синаном to provide a space where the михраб could be see from anywhere inside the building. The very large central space is accordingly arranged as an восьмиугольник, formed by 8 enormous pillars, and capped by a circular dome of 31,25 метра (100 фута) diameter and 43 метра (141 фута) high. Восьмиугольник is formed into a square with four semidomes, and externally by four exceptionally tall minarets, 83 метра (272 фута) tall. The building's plan is thus a circle inside восьмиугольника inside a square[71].
Mughal архитектура

Архитектура Великих Моголов, as seen in the abandoned imperial city of Фатехпур-Сикри and the Тадж-Махал complex, has a distinctive mathematical order and a strong эстетика based on Симметрия and harmony[11][72].
Тадж-Махал exemplifies Mughal архитектуру, both representing рай[73] and displaying the Mughal Emperor Шах-Джахан's power through its scale, Симметрия and costly decoration. The white marble мавзолей, decorated with Флорентийская мозаика[англ.], the great gate (Darwaza-i rauza), other buildings, the gardens and paths together form a unified hierarchical design. The buildings include a мечеть in red sandstone on the west, and an almost identical building, the Jawab or 'answer' on the east to maintain the bilateral Симметрия of the complex. The formal Чарбах[англ.] ('сад в четырёх частях') is in four parts, symbolising the four rivers of paradise, and offering views and reflections of the мавзолея. These are divided in turn into 16 parterres[74].

Тадж-Махал complex was laid out on a grid, subdivided into smaller grids. The historians of архитектуры Koch and Barraud agree with the traditional accounts that give the width of the complex as 374 Mughal yards or зира,[e] the main area being three 374-gaz squares. These were divided in areas like the bazaar and caravanserai into 17-gaz modules; the garden and terraces are in modules of 23 зиры, and are 368 зир wide (16 x 23). Мавзолей, мечеть and guest house are laid out on a grid of 7 зир. Koch and Barraud observe that if восьмиугольник, used repeatedly in the complex, is given sides of 7 units, then it has a width of 17 units,[f] which may help to explain the choice of ratios in the complex[75].
Христианская архитектура

a) Plan of gallery (upper half)
b) Plan of the ground floor (lower half)
Христианская патриаршая базилика собора Святой Софии в городе Византий (ныне Стамбул), построенный в 537 (и дважды перестроенный), был в течение тысячи лет[g] наибольшим кафедральным собором. Он стимулировал построение многих более поздних зданий, включая Мечеть Султанахмет и другие мечети города. Архитектура Византии включает притвор, увенчанный круглым куполом и два полукуполами, все одного диаметра (31м), с пятью меньшими полукуполами, образующими апсиду и четыре круглых угла просторного прямоугольного внутреннего пространства[76]. Это интерпретировалось средневековыми архитекторами как представление земного внизу (квадратное основание) и святых небес сверху (устремлённый ввысь сферический купол)[77]. Император Юстиниан I использовал двух геометров, Исидора Милетского и Исидора Милетского в качестве архитекторов. Исидор собрал труды Архимеда по стереометрии и был под его влиянием[12][78].
Важность крещения в воде в христианстве была отражена в архитектуре баптистерий. Наиболее старый, Латеранский баптистерий в Риме, построеных в 440[79], установил тенденцию восьмиугольных баптистерий. Купель внутри этих строений была часто восьмиугольной, хотя наиболее крупный итальянский баптистерий в Пизе, построенный между 1152 и 1363, имеет круглую форму с восьмиугольным резервуаром. Баптистерий имеет высоту 54,86 метра с диаметром 34,13 метра (отношение 8:5)[80]. Амвросий Медиоланский писал, что резервуары и баптистерии имели восьмиугольную форму, «поскольку на восьмой день[h] было вознесение, Христос ослабляет оковы смерти и получает мёртвых из их могил.»[81][82]. Аврелий Августин аналогично описывает восемь дней как «вечность ... освящёння воскрешением Христа»[82][83]. Восьмиугольный баптистерий Сент-Джона, Флоренция, построенный между 1059 и 1128, одно из наиболее старых зданий в городе, и одно из последних прямых традиций античности. Оно крайне сильно повлияло на флорентийских архитекторов и главные архитекторы той эпохи, включая Франческо Таленти, Alberti and Brunelleschi used it as the model of classical архитектуры[84].
The number five is used «exuberantly»[85] in the 1721 Церковь Святого Иоанна Непомука at Zelená hora, near Ждяр-над-Сазавоу in the Czech republic, designed by Jan Blažej Santini Aichel. The nave is circular, surrounded by five pairs of columns and five oval domes alternating with ogival апсиды. The church further has five gates, five chapels, five altars and five stars; a legend claims that when Ян Непомуцкий was martyred, five stars appeared over his head[85][86]. The fivefold архитектура may also symbolise the Пять ран Христа[англ.] and the five letters of «Tacui» (Latin: «я храню молчание» [about secrets of the исповедальни])[87].
Antoni Gaudí used a wide variety of geometric structures, some being Минимальная поверхностьs, in the Саграда-Фамилия, Барселона, started in 1882 (and not completed as of 2015). These include hyperbolic Параболоидs and hyperboloids of revolution,[88] замощений, Арка с очертанием обратной цепной линии[англ.]es, Катеноидs, Геликоидs, and ruled surfaces. This varied mix of geometries is creatively combined in different ways around the church. For example, in the Passion Façade of Саграда-Фамилия, Gaudí assembled stone «branches» in the form of hyperbolic Параболоидs, which overlap at their tops (directrices) without, therefore, meeting at a point. In contrast, in the colonnade there are hyperbolic Параболоидal surfaces that smoothly join other structures to form unbounded surfaces. Further, Gaudí exploits natural patterns, themselves mathematical, with колоннами derived from the shapes of trees, and lintels made from unmodified basalt naturally cracked (by cooling from molten rock) into шестиугольных столбов][англ.][89][90][88].
The 1971 Собор Успения Святой Марии, Сан-Франциско[англ.] has a двускатная крыша composed of eight segments of hyperbolic Параболоидs, arranged so that the bottom horizontal cross section of the roof is a square and the top cross section is a Christian cross. The building is a square 77,7 метра (250 фута) on a side, and 57,9 метра (190 фута) high[91]. The 1970 Cathedral of Brasília by Oscar Niemeyer makes a different use of a Гиперболоид structure; it is constructed from 16 identical concrete beams, each weighing 90 tonnes,[i] arranged in a circle to form Гиперболоид вращения, the white beams creating a shape like hands praying to heaven. Only the dome is visible from outside: most of the building is below ground[92][93][94][95].
Several medieval церкви в Скандинавии являются круглыми[англ.], including four on the Danish island of Bornholm. One of the oldest of these, Эстерларская церковь[англ.] from c. 1160, has a circular nave around a massive circular stone column, pierced with arches and decorated with a fresco. The circular structure has three storeys and was apparently fortified, the top storey having served for defence[96][97]
-
The vaulting of the nave of Собор Святой Софии, Стамбул (annotations), 562
-
Восьмиугольный Baptistry of Saint John, Florence, completed in 1128
-
Fivefold symmetries: Jan Santini Aichel's Церковь Святого Иоанна Непомука at Zelená hora, 1721
-
Oscar Niemeyer's Cathedral of Brasília, 1970
Математическое украшение
Исламское архитектурный декор

Исламские здания часто украшаются геометрическими орнаментами[англ.], в которых, как правило, используются математические мозаики, образованные керамическими плитками (гирих, Зулляйдж), которые могут быть сами по себе быть простыми или украшены полосками[12].В исламских орнаментах используются смметричные фигуры, такие как звёзды с шестью, восемью или кратные восьми точки. Некоторые из них основываются на мотивах печати Соломона, восьмиугольной звезды, сделанной из двух квадратов, повёрнутых на 45 градусов относительно друг друга[98]. Исламские орнаменты используют многие из 17 возможных групп обоев[англ.]*. В 1944 Эдит Мюллер показала, что в украшении ансамбля Альгамбра используется 11 групп обоев, а в 1986 Бранко Грюнбаум заявил, что нашёл 13 групп обоев в Альгамбра, настаивая при этом, что оставшиеся 4 группы не были найдены нигде в исламских орнаментах [98].
Современное архитектурное украшение
К концу 20-го века новые математические конструкции, такие как фрактальная геометрия and апериодичные замощения были подхвачены архитекторами для обеспечения интересной и привлекательной облицовки зданий [4]. В 1913, архитектор-модернист Адольф Лоз провозгласил: «Орнамент — это преступление»[99], оказав влияние на архитектурное мышление до конца 20-го века. В 21-м веке архитекторы снова начали использовать орнаменты. Орнаменты 21-го века сильно отличаются. Концертный зал и конференц-центр Хеннинга Ларсена[англ.] 2011года в Рейкьявике выглядит подобно стене из кристаллов и сделан из больших блоков стекла[99]. Здание Форейн Оффис Аркитект 2010-го года Равенсборнского колледжа[англ.] в Лондоне покрыт 28,000 анодированными алюминиевыми плитками красного, белого и коричневого цветов, связывая круглые окна различных размеров. Покрытие использует три типа плитки — равносторонний треугольник и два неправильных пятиугольника[100][101][j] Библиотека в Канадзаве[англ.] (архитекторы Кадзуми Кудо и Хироси Хориба из Coelacanth K&H Architects ) имеет декоративную решётку сделанную из маленьких круглых блоков стекла, вставленных в плоские бетонные стены [99].
-
Равенсборнский колледж[англ.], Лондон, 2010
-
Концертный зал и конференц-центр, Исландия, 2011
-
Библиотека в Канадзаве[англ.], Japan, 2011
-
Музей искусства Соумайя, Мехико, 2011
Крепости
Европа
Архитектура фортификационных сооружений эволюционировала из {{не переведено 5||Средневековые укрепления|средневековых укреплений|medieval fortification}, которые имели высокие каменные стены, к низкой симметричной бастионным системам укреплений, способных сопротивляться артиллерийскому обстрелу между середины пятнадцатого и девятнадцатым веками. Геометрия звёздной формы диктовалась необходимостью не допустить мёртвых зон, в которых атакующая пехота могла бы укрыться от огня защищающейся стороны. Стороны выступающих точек образовывали угол для возможности покрытия огнём всю поверхность и позволяли перекрёстный огонь (с двух сторон) с каждой выступающей точки. Хорошо известны архитекторы, разрабатывающие такую защиту, — Микеланджело, Бальдассаре Перуцци, Винченцо Скамоцци и Себастьен Ле Претр де Вобан[102][103].
Историк архитектуры Зигфрид Гидион говорил, что фортификационные сооружения в виде звёзд имели определяющее влияние на компоновку идеальных городов эпохи возрождения: «Эпоха возрождения была загипнотизирована одним типом городов, который в течение полутора веков — от Филарета до Скамоцци — был отпечатком всех утопических схем, это был город в виде звезды.»[104].
-
Куворден План фортификационного сооружения 17-го века
Китай

В архитектуре Китая тулоу провинции Фуцзян — это круглые структуры общественной защиты, главным образом, с сплошными стенами и одной покрытой железом деревянной дверью, датируемые шестнадцатым веком. Стены покрыты крышами, которые немного наклонены во внешнюю и внутренние стороны, образуя кольцо. Центр кольца является открытым мощёным внутренним двором, часто со стеной, окружающей укреплённые галереи высотой до пяти этажей [105].
Экологические цели

Архитекторы могут также выбирать форму здания из экологических соображений[85]. Например, Небоскрёб Мэри-Экс архитектурного бюро Foster and Partners, Лондон, известный как «Корнишон» за его подобную огурцу форму, является телом вращения, разработанный с использованием системы автоматизированного проектирования. Геометрия здания была выбрана не только исходя из эстетических причин, а чтобы минимизировать вихри воздуха у основания здания. Вопреки явно кривой поверхности, все панели стекла, образующие поверхность, являются плоскими, за исключением линзы на вершине здания. Большинство панелей квадратны, поскольку это позволяет вырезать стёкла с меньшими отходами[1].
Традиционный якчхал[англ.] (ледяная яма) в Персии функционирует подобно испарительного охладителя. Над поверхностью структура имеет вид купола, но имеет подземное место хранения для льда, а иногда и для пищи. Подземное пространство и толстая теплонепроницаемая конструкция изолирует пространство круглый год. Внутреннее пространство часто остужалось ветроуловителями. Лёд был доступен летом для приготовления холодного десерта фалуде[106].
См. также
Пояснения
- ↑ In Book 4, chapter 3 of De architectura, he discusses modules directly[15]
- ↑ Римский фут[англ.]* was about 0,296 метра (0,97 фута).
- ↑ In modern algebraic notation, these ratios are respectively 1:1, √2:1, 4:3, 3:2, 5:3, 2:1.
- ↑ Pace Nikos Salingaros, who suggests the contrary[39], but it is not clear exactly what Математика may be embodied in the curves of Ле Корбюзье's chapel.[40]
- ↑ 1 gaz is about 0,86 метра (2,8 фута).
- ↑ A square drawn around восьмиугольника by prolonging alternate sides adds four right angle triangles with hypotenuse of 7 and the other two sides of √(49/2) or 4,9497..., nearly 5. The side of the square is thus 5+7+5, which is 17.
- ↑ Вплоть до того, как Севильский кафедральный собор был завершён в 1520.
- ↑ Шестой день cтрастной седмицы был Великой пятницей. Последующие воскресенье (воскрешение) было, таким образом восьмым днём[81].
- ↑ This is 90 тонн (Шаблон:Convert/ton).
- ↑ Предполагалось апериодичное замозение, чтобы избежать ритма в решётке, но, на практике, мозаика Пенроуза была слишком сложной, так что была выбрана решётка рсзмером 2,625м по горизонтали и 4,55м по вертикали [101].
Примечания
- ↑ 1 2 3 Freiberger, 2007.
- ↑ 1 2 Rian, Park, Ahn, Chang, 2007, с. 4093–4107.
- ↑ Williams, Ostwald, 2015, с. chapter 1. 1–24.
- ↑ 1 2 Williams, Ostwald, 2015, с. 1-24, chapter 48.
- ↑ Overview.
- ↑ Leyton, 2001.
- ↑ Stakhov, Olsen, 2009.
- ↑ Smith, 1870, с. 620.
- ↑ 1 2 Vitruvius, 2009, с. 8–9.
- ↑ 1 2 Tennant, 2003.
- ↑ 1 2 Rai, 1993, с. 19–48.
- ↑ 1 2 3 4 5 6 7 O'Connor , Robertson, 2002.
- ↑ van den Hoeven, van der Veen, 2010.
- ↑ Cucker, 2013, с. 103–106.
- ↑ Vitruvius.
- ↑ Williams, Ostwald, 2015, с. 42, 48.
- ↑ Roth, 1992, с. 36.
- ↑ Claridge, 1998, с. 204–5.
- ↑ Lancaster, 2005, с. 44–46.
- ↑ March, 1996, с. 54–65.
- ↑ Mathalino.com.
- ↑ Typ 525.69.781, Houghton Library, Harvard University
- ↑ Andersen, 2008, с. 117–121.
- ↑ Ruhl.
- ↑ Copplestone, 1963, с. 251.
- ↑ Wassell.
- ↑ Palladio, 1997, с. book I, chapter xxi, page 57.
- ↑ Scamozzi, 2003.
- ↑ Borys, 2014, с. 140–148 and passim.
- ↑ Beckh, 2015, с. 75 and passim.
- ↑ The Engineer, 1897, с. 292–294.
- ↑ Graefe, 1990, с. 110–114.
- ↑ 1 2 Hatherley, 2011.
- ↑ Rietveld Schröderhuis.
- ↑ Historic England. Details from listed building database (1358981) (англ.). National Heritage List for England. Дата обращения: 5 октября 2015.
- ↑ Moholy-Nagy, 1938, с. 46.
- ↑ Gamwell, 2015, с. 306.
- ↑ Le Corbusier, 2004.
- ↑ 1 2 3 Salingaros.
- ↑ Greene.
- ↑ Hanser, 2006, с. 211.
- ↑ World Architecture Survey, 2010.
- ↑ Denver Airport Press Kit.
- ↑ Denver International Airport.
- ↑ Biosphere.
- ↑ Hahn, 2013.
- ↑ Salingaros, 2006, с. 139–141.
- ↑ Salingaros, 2006, с. 124–125.
- ↑ Gehry, Mudford, Koshalek, 2009.
- ↑ Garcetti, 2004.
- ↑ 1 2 Markowsky, 1992.
- ↑ Taseos, 1990.
- ↑ Gazale, 1999.
- ↑ 1 2 3 4 5 6 7 Cooke, 2011, с. 237–238.
- ↑ Gillings, 1982, с. 161.
- ↑ Kramrisch, 1976.
- ↑ Ifrah, 998.
- ↑ 1 2 Fractals in Indian Architecture.
- ↑ Jackson.
- ↑ King, 2005, с. 72.
- ↑ Maor, 2007, с. 19.
- ↑ 1 2 Norwich, 2001, с. 63.
- ↑ Penrose, 1973, с. ch. II.3, plate 9.
- ↑ Stevens, 1962, с. 337–338.
- ↑ Начала Евклида. Book 6, Proposition 30.
- ↑ Archibald.
- ↑ Applications of the Golden Mean to Architecture
- ↑ Gedal, 2011.
- ↑ Irwin, 2011, с. 109–112.
- ↑ Robertson, 2007.
- ↑ Blair, Bloom, 1995.
- ↑ Michell, Pasricha, 2011.
- ↑ Parker, 2010, с. 224.
- ↑ Koch, 2006, с. 24 and passim.
- ↑ Koch, 2006, с. 104–109.
- ↑ Fazio, Moffett, Wodehouse, 2009.
- ↑ Gamwell, 2015, с. 48.
- ↑ Kleiner, Mamiya, 2008, с. 329.
- ↑ Menander, Brandt, Appetechia, Thorén, 2010.
- ↑ The Baptistery.
- ↑ 1 2 Huyser-Konig.
- ↑ 1 2 Kuehn, 1992, с. 53–60.
- ↑ Augustine of Hippo, 426, с. Book 22, Chapter 30.
- ↑ Kleiner, 2012, с. 355–356.
- ↑ 1 2 3 Simitch, Warke, 2014, с. 191.
- ↑ Zelená hora.
- ↑ Saint John of Nepomuk.
- ↑ 1 2 Burry, Burry, Dunlop, Maher, 2001.
- ↑ Geometry of Antoni Gaudi.
- ↑ Usvat.
- ↑ Nervi.
- ↑ Brasilia Cathedral.
- ↑ Behrends, Crato, Rodrigues, 2012, с. 143.
- ↑ Emmer, 2012, с. 111.
- ↑ Mkrtchyan, 2013.
- ↑ Nordens kirker.
- ↑ Natur Bornholm.
- ↑ 1 2 Rønning.
- ↑ 1 2 3 Gibberd, Hill, 2013.
- ↑ Ravensbourne College, 2010.
- ↑ 1 2 Bizley.
- ↑ Duffy, 1975.
- ↑ Chandler, 1990.
- ↑ Giedion, 1962, с. 43.
- ↑ O'Neill, 2015.
- ↑ Mahdavinejad, Javanrudi, 2012.
Литература
- Iasef Md Rian, Jin-Ho Park, Hyung Uk Ahn, Dongkuk Chang. Fractal geometry as the synthesis of Hindu cosmology in Kandariya Mahadev temple, Khajuraho // Building and Environment. — 2007. — Т. 42. — doi:10.1016/j.buildenv.2007.01.028.
- Architectural Engineering Overview. Sloan Career Cornerstone Center. Дата обращения: 27 октября 2017.
- Michael Leyton. A Generative Theory of Shape. — Springer, 2001. — ISBN 978-3-540-42717-9.
- Alexey Stakhov, Olsen Olsen. The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science. — World Scientific, 2009. — ISBN 978-981-277-582-5.
- William Smith. Dictionary of Greek and Roman Biography and Mythology. — Little, Brown, 1870. — С. 620.
- Saskia van den Hoeven, Maartje van der Veen. Muqarnas: Mathematics in Islamic Arts. — Utrecht University, 2010.
- Felipe Cucker. Manifold Mirrors: The Crossing Paths of the Arts and Mathematics. — Cambridge University Press, 2013. — С. 103–106. — ISBN 978-0-521-72876-8.
- Architecture and Mathematics from Antiquity to the Future: Volume I: from Antiquity to the 1500s / Kim Williams, Michael J. Ostwald. — Birkhäuser, 2015. — С. chapter 1. 1–24. — ISBN 978-3-319-00136-4.
- Architecture and Mathematics from Antiquity to the Future Volume II: The 1500s to the Future / Kim Williams, Michael J. Ostwald. — Birkhäuser, 2015. — ISBN 978-3-319-00142-5.
- Vitruvius. VITRUVIUS, BOOK IV, CHAPTER 3 On the Doric order. Vitruvius.be. Дата обращения: 6 октября 2015.
- Vitruvius. On Architecture. — Penguin Books, 2009. — ISBN 978-0-14-193195-1.
- Kim Williams, Michael J. Ostwald. Architecture and Mathematics from Antiquity to the Future Volume I: Antiquity to the 1500s. — Birkhäuser, 2015. — ISBN 978-3-319-00137-1.
- Leland M. Roth. Understanding Architecture: Its Elements, History, And Meaning. — Boulder: Westview Press, 1992. — ISBN 0-06-438493-4.
- Amanda Claridge. Rome. — Oxford Oxfordshire: Oxford University Press, 1998. — (Oxford Archaeological Guides). — ISBN 0-19-288003-9.
- Lynne C. Lancaster. Concrete Vaulted Construction in Imperial Rome: Innovations in Context. — Cambridge: Cambridge University Press, 2005. — С. 44–46. — ISBN 0-521-84202-6.
- Lionel March. Renaissance mathematics and architectural proportion in Alberti's De re aedificatoria // Architectural Research Quarterly. — 1996. — Т. 2, вып. 1. — С. 54–65. — doi:10.1017/S135913550000110X.
- Sphere circumscribing a cube. Mathalino.com Engineering Math Review. Дата обращения: 4 октября 2015.
- Kirsti Andersen. The Geometry of an Art: The History of the Mathematical Theory of Perspective from Alberti to Monge. — Springer, 2008. — ISBN 978-0-387-48946-9.
- Carsten Ruhl. Palladianism: From the Italian Villa to International Architecture. — European History Online, 2011. — Апрель.
- Trewin Copplestone. World Architecture. — Hamlyn, 1963.
- Stephen R. Wassell. The Mathematics Of Palladio's Villas: Workshop '98. — Nexus Network Journal.
- Andrea Palladio. I quattro libri dell'architettura. — MIT Press, 1997. — С. book I, chapter xxi. Год изиния оригинала - 1570
- Vincenzo Scamozzi, Vroom W. H. M. (перевод). The Idea of a Universal Architecture. — Architectura & Natura, 2003. Год изиния оригинала -1615
- Ann Marie Borys. Vincenzo Scamozzi and the Chorography of Early Modern Architecture. — Ashgate Publishing, 2014. — ISBN 978-1-4094-5580-6.
- Matthias Beckh. Hyperbolic Structures: Shukhov's Lattice Towers - Forerunners of Modern Lightweight Construction. — John Wiley & Sons, 2015. — ISBN 978-1-118-93268-1.
- The Nijni-Novgorod exhibition: Water tower, room under construction, springing of 91 feet span // The Engineer. — London, 1897. — Март. — С. 292-294.
- Rainer. Vladimir G. Suchov 1853—1939. Die Kunst der sparsamen Konstruktion. — Deutsche Verlags-Anstalt, 1990. — С. 110–114. — ISBN 3-421-02984-9.
- Owen Hatherley. The Constructivists and the Russian Revolution in Art and Architecture // The Guardian. — 2011. — Ноябрь.
- Rietveld Schröderhuis (Rietveld Schröder House). — UNESCO.
- Laszlo Moholy-Nagy, Daphne M. Hoffman (перевод). The New Vision: Fundamentals of Design, Painting, Sculpture, Architecture. — New Bauhaus Books, 1938.
- Lynn Gamwell. Mathematics and Art: A Cultural History. — Princeton University Press, 2015. — ISBN 978-0-691-16528-8.
- Le Corbusier. The Modulor: A Harmonious Measure to the Human Scale, Universally Applicable to Architecture and Mechanics. — Birkhäuser, 2004. — ISBN 3-7643-6188-3. Год издания оригинала -1954, 1958
- Herb Greene. Le Corbusier: Notre Dame du Haut at Ronchamp. Дата обращения: 5 октября 2015.
- David A. Hanser. Architecture of France. — Greenwood Publishing Group, 2006. — ISBN 978-0-313-31902-0.
- Vanity Fair's World Architecture Survey: the Complete Results. — 2010. — Июнь.
- Denver International Airport Press Kit. — Fenstress Architects, 2013.
- Необходимо задать параметр
url=в шаблоне {{cite web}}. [ http://www.aviewoncities.com/montreal/biosphere.htm]. A view on cities. Дата обращения: 1 октября 2015. - Alexander J. Hahn. Mathematical Excursions To Architecture. — Inside Science, 2013. — Февраль.
- Nikos Salingaros. A Theory of Architecture. — Umbau, 2006.
- Frank O. Gehry, Grant Mudford, Richard Koshalek. Symphony: Frank Gehry's Walt Disney Concert Hall. — Five Ties, 2009.
- Gil Garcetti. Iron: Erecting the Walt Disney Concert Hall. — Princeton Architectural Press, 2004.
- Nikos Salingaros. Architecture, Patterns, and Mathematics // Nexus Network Journal. — Т. 1, вып. 2.
- George Markowsky. Misconceptions About the Golden Ratio // The College Mathematics Journal. — 1992. — Январь (т. 23, вып. 1).
- Socrates G. Taseos. Back in Time 3104 B.C. to the Great Pyramid. — SOC Publishers, 1990.
- Midhat Gazale. Gnomon: From Pharaohs to Fractals. — Princeton University Press, 1999.
- Roger L. Cooke. The History of Mathematics: A Brief Course. — 2nd. — John Wiley & Sons, 2011. — ISBN 978-1-118-03024-0.
- Richard J. Gillings. Mathematics in the Time of the Pharaohs. — Dover, 1982.
- Stella Kramrisch. . — The Hindu Temple, 1976. — Т. 1 & 2. — ISBN 81-208-0223-3.
- Vibhuti Sachdev, Giles Tillotson. Building Jaipur: The Making of an Indian City. — 2004. — ISBN 978-1-86189-137-2.
- Georges Ifrah. A Universal History of Numbers. — Penguin, 1998.
- Fractals in Indian Architecture. — Yale University.
- William J. Jackson. For All Fractal Purposes ... an introduction. — Indiana University-Purdue University Indianapolis. Архивировано 14 сентября 2015 года.
- Anthony D. King. Buildings and Society: Essays on the Social Development of the Built Environment. — Taylor & Francis, 2005. — ISBN 0-203-48075-9.
- O'Connor J. J., Robertson E. F. Mathematics and Architecture. — University of St Andrews, 2002. — Февраль.
- Eli Maor. The Pythagorean Theorem: A 4,000-year History. — Princeton University Press, 2007. — ISBN 0-691-12526-0.
- John Julius Norwich. Great Architecture of the World. — Artists House, 2001.
- Francis Penrose. Principles of Athenian Architecture. — Society of Dilettanti, 1973. Год оригинального издания =1851
- Gorham P. Stevens. Concerning the Impressiveness of the Parthenon // American Journal of Archaeology. — 1962. — Июль (т. 66, вып. 3). — С. 337–338. — doi:10.2307/501468.
- Archibald R. C. Notes on the Logarithmic Spiral, Golden Section and the Fibonacci Series. Дата обращения: 1 октября 2015.
- George Markowsky. Misconceptions about the Golden Ratio // The College Mathematics Journal. — 1992. — Январь (т. 23, вып. 1).
- Najib Gedal. The Great Mosque of Cordoba: Geometric Analysis. — Islamic Art & Architecture, 2011.
- Raymond Tennant. International Joint Conference of ISAMA, the International Society of the Arts, Mathematics, and Architecture, and BRIDGES. Mathematical Connections in Art Music, and Science, University of Granada, Spain, July, 2003. Islamic Constructions: The Geometry Needed by Craftsmen. // International Joint Conference of ISAMA, the International Society of the Arts, Mathematics, and Architecture, and BRIDGES, Mathematical Connections in Art Music, and Science. — 2003. — Июль.
- Robert Irwin. The Alhambra. — Profile Books, 2011. — ISBN 1-84765-098-8.
- Ann Robertson. Revisiting the Geometry of the Sala de Dos Hermanas. — BRIDGES, 2007.
- Sheila Blair, Jonathan M. Bloom. The Art and Architecture of Islam 1250-1800. — Yale University Press, 1995. — ISBN 0-300-06465-9.
- Jaswant Rai. Mathematics and Aesthetics in Islamic Architecture: Reference to Fatehpur Sikri // Journal of King Saud University, Architecture & Planning. — 1993. — Т. 5, вып. 1.
- George Michell, Amit Pasricha. Mughal Architecture & Gardens. — Antique Collectors Club, 2011. — ISBN 978-1-85149-670-9.
- Philip Parker. World History. — Dorling Kindersley, 2010. — ISBN 978-1-4053-4124-0.
- Ebba Koch. The Complete Taj Mahal: And the Riverfront Gardens of Agra. — Thames & Hudson, 2006. — С. 24 and passim. — ISBN 0-500-34209-1.
- Ebba Koch. The Complete Taj Mahal: And the Riverfront Gardens of Agra. — Thames & Hudson, 2006. — ISBN 0-500-34209-1.
- Michael Fazio, Marian Moffett, Lawrence Wodehouse. Buildings Across Time. — McGraw-Hill Higher Education, 2009. — ISBN 978-0-07-305304-2.
- Lynn Gamwell. Mathematics and Art: A Cultural History. — Princeton University Press, 2015. — ISBN 978-0-691-16528-8.
- Fred S. Kleiner, Christin J. Mamiya. Gardner's Art Through the Ages: Volume I, Chapters 1–18. — Wadsworth, 2008. — ISBN 0-495-46740-5.
- Hanna Menander, Olof Brandt, Agostina Appetechia, Håkan Thorén. The Lateran Baptistery in Three Dimensions. — Swedish National Heritage Board, 2010.
- Необходимо задать параметр
url=в шаблоне {{cite web}}. [ The Baptistery]. The Leaning Tower of Pisa. Дата обращения: 30 октября 2015. - Joan Huyser-Konig. Theological Reasons for Baptistry Shapes. Calvin Institute of Christian Worship. Дата обращения: 30 октября 2015.
- Regina Kuehn. A Place for Baptism. — Liturgy Training Publications, 1992. — С. 53–60. — ISBN 978-0-929650-00-5.
- Augustine of Hippo. The City of God. — 426. — С. Book 22, Chapter 30.
- Fred Kleiner. Gardner's Art through the Ages: A Global History. — Cengage Learning, 2012. — ISBN 1-133-71116-2.
- Zelená hora near Žďár nad Sázavou. Czech Tourism. Дата обращения: 10 ноября 2015.
- Attributes of Saint John of Nepomuk. Saint John of Nepomuk. Дата обращения: 10 ноября 2015.
- Burry M.C., Burry J.R., Dunlop G.M., Maher A. Drawing Together Euclidean and Topological Threads (pdf). — Dunedin, New Zealand: University of Otago, 2001. Архивировано 31 октября 2007 года.
- Marianne Freiberger. Perfect buildings: the maths of modern architecture. — Plus magazine, 2007. — Март.
- Andrea Simitch, Val Warke. The Language of Architecture: 26 Principles Every Architect Should Know. — Rockport Publishers, 2014. — ISBN 978-1-62788-048-0.
- The Geometry of Antoni Gaudi. Math & the Art of MC Escher. Saint Louis University Mathematics and Computer Science. Дата обращения: 4 октября 2015.
- Liliana Usvat. Antony Gaudi and Mathematics. — Mathematics Magazine.
- Burry M.C., Burry J.R., Dunlop G.M., Maher A. Drawing Together Euclidean and Topological Threads. — The 13th Annual Colloquium of the Spatial Information Research Centre, University of Otago, Dunedin, New Zealand, 2001. Архивировано 25 июня 2008 года.
- Pier Luigi Nervi. Cathedral of Saint Mary of the Assumption. Architectuul. Дата обращения: 12 октября 2015.
- Brasilia Cathedral. About Brasilia. Дата обращения: 13 ноября 2015.
- Ehrhard Behrends, Nuno Crato, Jose Francisco Rodrigues. Raising Public Awareness of Mathematics. — Springer Science & Business Media, 2012. — ISBN 978-3-642-25710-0.
- Michele Emmer. Imagine Math: Between Culture and Mathematics. — Springer Science & Business Media, 2012. — ISBN 978-88-470-2427-4.
- Ruzanna Mkrtchyan. Cathedral of Brasilia. — Building.AM, 2013.
- Østerlars kirke (неопр.). Nordens kirker. Дата обращения: 2 декабря 2016.
- Østerlars kirke (неопр.). Natur Bornholm. Дата обращения: 2 декабря 2016.
Frode Rønning,. Islamic Patterns And Symmetry Groups. — University of Exeter, 2009.
- Matt Gibberd, Albert Hill. The Return of Ornamentation // The Telegraph. — 2013. — Август.
- Ravensbourne College by Foreign Office Architects. — de zeen magazine, 2010. — Сентябрь.
- Bizley, Graham FOA's peninsula patterns for Ravensbourne College. bdonline.co.uk. Дата обращения: 16 октября 2015.
- Duffy C. Fire & Stone, The Science of Fortress Warfare 1660–1860. — Booksales, 1975. — ISBN 978-0-7858-2109-0.
- David Chandler. The Art of Warfare in the Age of Marlborough. — Spellmount, 1990. — ISBN 978-0-946771-42-4.
- Siegfried Giedion. Space, Time and Architecture. — Harvard University Press, 1962. Год издания оригинальной статьи - 1941
- Tom O'Neill. China's Remote Fortresses Lose Residents, Gain Tourists. — National Geographic, 2015. — Январь.
- Mahdavinejad M., Kavan Javanrudi. Assessment of Ancient Fridges: A Sustainable Method to Storage Ice in Hot-Arid Climates // Asian Culture and History. — 2012. — Июль (т. 4, вып. 2). — doi:10.5539/ach.v4n2p133.
Ссылки
- Nexus Network Journal: Architecture and Mathematics Online
- The International Society of the Arts, Mathematics, and Architecture
- University of St Andrews: Mathematics and Architecture
- National University of Singapore: Mathematics in Art and Architecture
- Dartmouth College: Geometry in Art & Architecture
![Новая Вещественность[англ.]: Walter Gropius's Bauhaus, Дессау, 1925](http://upload.wikimedia.org/wikipedia/commons/thumb/3/36/Bauhaus-Dessau_Wohnheim_Balkone.jpg/113px-Bauhaus-Dessau_Wohnheim_Balkone.jpg)
![Цилиндр: Charles Holden's станция лондонской подземки в Арнос Гроув[англ.], 1933](http://upload.wikimedia.org/wikipedia/commons/thumb/9/97/Arnos_Grove_underground_station_16_November_2012.jpg/120px-Arnos_Grove_underground_station_16_November_2012.jpg)







![Собор Успения Святой Марии, Сан-Франциско[англ.], 1971](http://upload.wikimedia.org/wikipedia/commons/thumb/3/34/St_Mary%27s_Cathedral_-_San_Francisco.jpg/120px-St_Mary%27s_Cathedral_-_San_Francisco.jpg)
![Central column of Эстерлара[англ.] Северные круглые церкви[англ.] in Bornholm, Denmark](http://upload.wikimedia.org/wikipedia/commons/thumb/b/ba/Oesterlarsfresco.jpg/120px-Oesterlarsfresco.jpg)
![Равенсборнский колледж[англ.], Лондон, 2010](http://upload.wikimedia.org/wikipedia/commons/thumb/e/e4/London_MMB_%C2%ABT1_Ravensbourne_College.jpg/120px-London_MMB_%C2%ABT1_Ravensbourne_College.jpg)
![Библиотека в Канадзаве[англ.], Japan, 2011](http://upload.wikimedia.org/wikipedia/commons/thumb/5/55/Umimirai_Library.jpg/120px-Umimirai_Library.jpg)



![Нёф-Бризах, Эльзас, одно из фортификационных сооружений Вобана[англ.]](http://upload.wikimedia.org/wikipedia/commons/thumb/0/0d/Neuf-Brisach_007_850.jpg/120px-Neuf-Brisach_007_850.jpg)