Пифагорова тройка

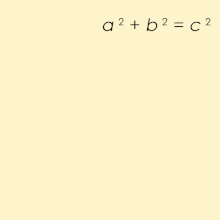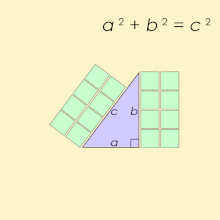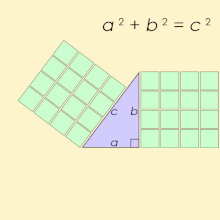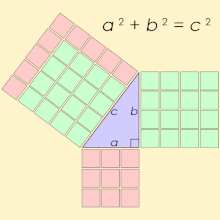
Пифаго́рова тро́йка — упорядоченный набор из трёх натуральных чисел удовлетворяющих следующему однородному квадратному уравнению
При этом числа, образующие пифагорову тройку, называются пифагоровыми числами. Названы в честь Пифагора Самосского, хотя открыты задолго до него.
Треугольник, длины сторон которого образуют пифагорову тройку, является прямоугольным и называется пифагоровым треугольником.
Примитивные тройки[править | править код]
Поскольку уравнение однородно, при умножении , и на одно и то же натуральное число получится другая пифагорова тройка. Пифагорова тройка называется примитивной, если она не может быть получена таким способом из какой-то другой пифагоровой тройки, то есть если являются взаимно простыми числами. Другими словами, наибольший общий делитель примитивной пифагоровой тройки равен 1.
В примитивной тройке числа и имеют разную чётность, причём чётное делится на 4, а — всегда нечётно.
Любая примитивная пифагорова тройка , где — нечётно, а — чётно, однозначно представляется в виде для некоторых натуральных взаимно простых чисел разной чётности.
Эти числа можно вычислить по формулам
Наоборот, любая такая пара чисел задаёт примитивную пифагорову тройку [1].
Примеры[править | править код]
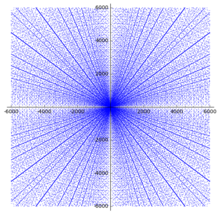
Имеется 16 примитивных пифагоровых троек с :
| (3, 4, 5) | (5, 12, 13) | (8, 15, 17) | (7, 24, 25) |
| (20, 21, 29) | (12, 35, 37) | (9, 40, 41) | (28, 45, 53) |
| (11, 60, 61) | (16, 63, 65) | (33, 56, 65) | (48, 55, 73) |
| (13, 84, 85) | (36, 77, 85) | (39, 80, 89) | (65, 72, 97) |
Не все тройки с примитивны, например, (6, 8, 10) получается умножением на два тройки (3, 4, 5). Каждая из троек с небольшой гипотенузой образует хорошо различимую радиальную прямую из кратных ей троек на диаграмме рассеяния.
Примитивные тройки с :
| (20, 99, 101) | (60, 91, 109) | (15, 112, 113) | (44, 117, 125) |
| (88, 105, 137) | (17, 144, 145) | (24, 143, 145) | (51, 140, 149) |
| (85, 132, 157) | (119, 120, 169) | (52, 165, 173) | (19, 180, 181) |
| (57, 176, 185) | (104, 153, 185) | (95, 168, 193) | (28, 195, 197) |
| (84, 187, 205) | (133, 156, 205) | (21, 220, 221) | (140, 171, 221) |
| (60, 221, 229) | (105, 208, 233) | (120, 209, 241) | (32, 255, 257) |
| (23, 264, 265) | (96, 247, 265) | (69, 260, 269) | (115, 252, 277) |
| (160, 231, 281) | (161, 240, 289) | (68, 285, 293) |
Возможные значения в пифагоровых тройках образуют последовательность (последовательность A009003 в OEIS)
- 5, 10, 13, 15, 17, 20, 25, 26, 29, 30, 34, 35, 37, 39, 40, 41, 45, 50, …
Основываясь на свойствах чисел Фибоначчи, можно образовывать из этих чисел, например, такие пифагоровы тройки:
История[править | править код]

Наиболее известной в развитых древних культурах была тройка (3, 4, 5), которая позволяла древним строить прямые углы. Витрувий считал эту тройку высшим достижением математики, а Платон — символом супружества, что говорит о большом значении, которое придавали древние тройке (3, 4, 5).
В архитектуре древнемесопотамских надгробий встречается равнобедренный треугольник, составленный из двух прямоугольных со сторонами 9, 12 и 15 локтей. Пирамиды фараона Снофру (XXVII век до н. э.) построены с использованием треугольников со сторонами 20, 21 и 29, а также 18, 24 и 30 десятков египетских локтей.
Вавилонские математики умели вычислять пифагоровы тройки. Вавилонская глиняная табличка, названная Plimpton 322, содержит пятнадцать пифагоровых троек (точнее пятнадцать пар чисел , таких что ). Считается, что эта табличка была создана около 1800 года до н. э.[2]
Генерация троек[править | править код]


Формула Евклида[3] является основным средством построения пифагоровых троек. Согласно ей для любой пары натуральных чисел и () целые числа
образуют пифагорову тройку. Тройки, образованные по формуле Евклида, примитивны тогда и только тогда, когда и взаимно просты и нечётно. Если и , и нечётны, то , и будут чётными и тройка не примитивна. Однако деление , и на 2 даёт примитивную тройку, если и взаимно просты[4].
Любая примитивная тройка получается из единственной пары взаимно простых чисел и , одно из которых чётно. Отсюда следует, что существует бесконечно много примитивных пифагоровых троек.
Несмотря на то, что формула Евклида генерирует все примитивные тройки, она не порождает все тройки. При добавлении дополнительного параметра получается формула, порождающая все пифагоровы треугольники единственным образом:
где , и — натуральные числа, , нечётно, и взаимно просты.
То, что эти формулы образуют пифагоровы тройки, можно проверить путём подстановок в и проверки, что результат совпадает с . Поскольку любую пифагорову тройку можно разделить на некоторое , чтобы получить примитивную тройку, любая тройка может быть образована единственным образом с использованием и для создания примитивной тройки, а затем она умножается на .
Со времён Евклида было найдено множество формул для генерации троек.
Доказательство формул Евклида[править | править код]
Тот факт, что числа , , , удовлетворяющие формуле Евклида, всегда составляют пифагоров треугольник, очевиден для положительных целых и , , поскольку после подстановки в формулы , и будут положительными числами, а также из того, что выполняется
Обратное утверждение, что , , выражаются формулой Евклида для любой пифагоровой тройки, вытекает из следующего[5]. Все такие тройки можно записать в виде (, , ), где , и , , являются взаимно простыми, а и имеют противоположную чётность (одно из них чётно, другое нечётно). (Если имеет ту же самую чётность с обоими катетами, то в случае их чётности они не будут взаимно простыми, а в случае нечётности даст чётное число, и оно не может быть равно нечётному .) Из мы получаем , а следовательно, . Тогда . Поскольку является рациональным, мы представим его в виде несократимой дроби . Мы отсюда же получаем, что дробь равна . Решая уравнения
относительно и , получим
Поскольку и несократимы по предположению, числители и знаменатели будут равными тогда и только тогда, когда правые части каждого равенства несократимы. Как мы условились, дробь тоже несократима, откуда следует, что и взаимно просты. Правые части будут несократимы тогда и только тогда, когда и имеют противоположную чётность, так что числитель не делится на 2. (А и должны иметь противоположную чётность — оба не могут быть чётными ввиду несократимости, а в случае нечётности обоих чисел деление на 2 даст дробь, в числителе и знаменателе которой будут нечётные числа, но эта дробь равна , в которой числитель и знаменатель будут иметь различную чётность, что противоречит предположению.) Теперь, приравнивая числители и знаменатели, получим формулу Евклида , , с и взаимно простыми и имеющими различную чётность.
Более длинное, но и более общепринятое доказательство приведено в книгах Маора (Maor, 2007)[6] и Серпинского[7].
Интерпретация параметров в формуле Евклида[править | править код]
Пусть стороны пифагорова треугольника равны , и . Обозначим угол между катетом и гипотенузой буквой . Тогда[8]
Обозначим угол между катетом 2mn и гипотенузой m^2 + n^2 буквой ψ. Тогда
tg ψ = (m^2 - n^2) / 2mn,
tg ψ/2 = n/m.
Элементарные свойства примитивных пифагоровых троек[править | править код]
Свойства примитивной пифагоровой тройки (a, b, c), где a < b < c (без указания чётности чисел a или b):
- всегда является полным квадратом[9]. Это особенно полезно для проверки, является ли заданная тройка чисел пифагоровой, хотя это и не является достаточным условием. Тройка (6, 12, 18) проходит этот тест, поскольку (c − a)(c − b)/2 является полным квадратом, но эта тройка не является пифагоровой. Если тройка чисел a, b и c образует пифагорову тройку, то число (c минус чётный катет) и половина числа (c минус нечётный катет) являются полными квадратами, однако это не является достаточным условием, и тройка (1, 8, 9) является контрпримером, поскольку 12 + 82 ≠ 92.
- Максимум одно из чисел a, b и c является квадратом[10].
- Площадь пифагорова треугольника не может быть квадратом[11] или удвоенным квадратом[12] натурального числа.
- В точности одно из чисел a и b нечётно, c всегда нечётно[13].
- В точности одно из чисел a и b делится на 3[14].
- В точности одно из чисел a и b делится на 4[7].
- В точности одно из чисел a, b и c делится на 5[7].
- Максимальное число, которое всегда делит произведение abc, равно 60[15].
- Все простые множители c являются простыми вида 4n + 1[16]. Таким образом, c имеет вид 4n + 1.
- Число (b − a) является произведением простых чисел вида 8n ± 1, то есть не имеет таких сомножителей, как 2, 3, 5, 11, 13, 19, 29, 37, 43, 53, 59, 61, 67, 83, 101, ...
- Площадь (K = ab/2) является чётным конгруэнтным числом[17].
- В любой пифагоровой тройке радиус вписанной окружности и радиусы трёх вневписанных окружностей являются натуральными числами. В частности, для примитивной тройки радиус вписанной окружности равен r = n(m − n), а радиусы вневписанных окружностей, касающихся катетов m2 − n2, 2mn, и гипотенузы m2 + n2 равны соответственно m(m − n), n(m + n) и m(m + n)[18].
- Как и для любого прямоугольного треугольника, обратное утверждение к теореме Фалеса гласит, что диаметр описанной окружности равен гипотенузе. Поскольку для примитивных троек диаметр равен √m2 + n2, радиус описанной окружности является половиной этого числа и это число рациональное, но не целое (поскольку m и n имеют разную чётность).
- Если площадь пифагорова треугольника умножить на кривизны вписанной окружности и трёх вневписанных, в результате получим четыре положительных целых w > x > y > z соответственно. Эти числа w, x, y, z удовлетворяют уравнению декартовых окружностей[19]. Эквивалентно, радиус внешней окружности Содди любого прямоугольного треугольника равен его полупериметру. Внешний центр Содди расположен в точке D, где ACBD — прямоугольник, ACB — прямоугольный треугольник, а AB — его гипотенуза[20].
- Не существует пифагоровых троек, для которых гипотенуза и один из катетов являются катетами другой пифагоровой тройки. Это одна из формулировок теоремы Ферма о прямоугольном треугольнике[21].
- Каждый примитивный пифагоров треугольник имеет уникальное отношение площади к квадрату полупериметра (то есть отношения для различных примитивных треугольников различны), и это отношение равно[22]
- Ни в каком примитивном пифагоровом треугольнике высота, опирающаяся на гипотенузу, не выражается целым числом, а потому он не может быть разбит на два пифагоровых треугольника[23].
Кроме того, могут существовать специальные пифагоровы тройки с некоторыми дополнительными свойствами:
- Любое целое, большее 2, которое не сравнимо с 2 по модулю 4 (другими словами, если оно больше 2 и не имеет вид 4n + 2) является частью примитивной пифагоровой тройки.
- Любое целое число, большее 2, входит в примитивную или непримитивную пифагорову тройку. Например, числа 6, 10, 14 и 18 не содержатся ни в какой примитивной тройке, но входят в тройки 6, 8, 10; 14, 48, 50 и 18, 80, 82.
- Существует бесконечно много пифагоровых троек, в которых гипотенуза и больший из катетов отличаются ровно на единицу (такие тройки заведомо примитивны). Один из способов получения таких троек — равенство (2n + 1)2 + [2n(n + 1)]2 = [2n(n + 1) + 1]2, приводящее к тройкам (3, 4, 5), (5, 12, 13), (7, 24, 25), и т. д. Более общее утверждение: для любого нечётного целого j существует бесконечно много примитивных пифагоровых троек, в которых гипотенуза и чётный катет отличаются на j2.
- Существует бесконечно много примитивных пифагоровых троек, в которых гипотенуза и больший по длине катет отличается ровно на два. Обобщение: Для любого целого k > 0, существует бесконечно много примитивных пифагоровых троек, в которых гипотенуза и нечётный катет отличаются на 2k2.
- Существует бесконечно много пифагоровых троек, в которых два катета отличаются ровно на единицу. Например, 202 + 212 = 292.
- Для любого натурального n существует n пифагоровых троек с различными гипотенузами и одной и той же площадью.
- Для любого натурального n существует по меньшей мере n различных пифагоровых троек с одним и тем же катетом a, где a — некоторое натуральное число
- Для любого натурального n существует по меньшей мере n различных пифагоровых троек с одной и той же гипотенузой[24].
- Существует бесконечно много пифагоровых троек, у которых квадратами являются гипотенуза c и сумма катетов a + b. В наименьшей такой тройке[25] a = 4 565 486 027 761; b = 1 061 652 293 520; c = 4 687 298 610 289. Здесь a + b = 2 372 1592 и c = 2 165 0172. В формуле Евклида эти значения соответствуют m = 2 150 905 и n = 246 792.
- Существуют пифагоровы треугольники с целой высотой, опирающейся на гипотенузу. Такие треугольники известны как разбиваемые, поскольку их можно разбить этой высотой на два меньших пифагоровых треугольника. Ни один из разбиваемых треугольников не образован примитивной тройкой[26].
- Множество всех примитивных пифагоровых треугольников образует корневое тернарное дерево естественным способом, см. Дерево примитивных пифагоровых троек.
Неизвестно, существуют ли две различные пифагоровы тройки с одинаковым произведением входящих в них чисел[27].
Геометрия формулы Евклида[править | править код]


Формулу Евклида для пифагоровой тройки
можно понять в терминах геометрии рациональных точек на единичной окружности [28]. Пусть имеется треугольник с катетами a и b и гипотенузой c, где a, b и c — положительные целые. По теореме Пифагора a2 + b2 = c2, а после деления обеих сторон на c2
Геометрически, точка на декартовой плоскости с координатами
лежит на единичной окружности x2 + y2 = 1. В этом уравнении координаты x и y задаются рациональными числами. И обратно, любая точка на окружности с рациональными координатами x и y даёт примитивную пифагорову тройку. В самом деле, запишем x и y как несократимые дроби:
где наибольший общий делитель чисел a, b и c равен 1. Поскольку точка с координатами x и y лежит на единичной окружности, то
что и требовалось доказать.

Таким образом, существует соответствие между точками с рациональными координатами на единичной окружности и примитивными пифагоровыми треугольниками. Исходя из этого, формулы Евклида можно получить методами тригонометрии или с использованием стереографической проекции.
Для применения стереографического подхода предположим, что P′ является точкой на оси x с рациональными координатами
Тогда с помощью алгебраических вычислений можно показать, что точка P имеет координаты
Таким образом, получаем, что любая рациональная точка оси x соответствует рациональной точке единичной окружности. И обратно, пусть P(x, y) — точка единичной окружности с рациональными координатами x и y. Тогда стереографическая проекция P′ на ось x имеет рациональные координаты
В терминах алгебраической геометрии алгебраическое многообразие рациональных точек единичной окружности является бирациональным к аффинной прямой над рациональными числами. Единичная окружность тогда называется рациональной кривой. Соответствие рациональных точек прямой и окружности даёт возможность дать явную параметризацию (рациональных) точек на окружности с помощью рациональных функций.
Группа пифагоровых троек[править | править код]
Любая рациональная точка на единичной окружности соответствует пифагоровой тройке (a, b, c), точнее — обобщённой пифагоровой тройке, так как a и b могут быть нулевыми и отрицательными.
Пусть даны два пифагоровых треугольника (a1, b1, c1) и (a2, b2, c2) с углами α и β. Можно построить треугольники с углами α ± β, используя формулы сложения углов:
Эти прямоугольные треугольники тоже будут целочисленными, то есть пифагоровыми. Можно ввести операцию над тройками, используя вышеприведённые формулы. Эта операция будет коммутативной и ассоциативной, то есть обобщённые пифагоровы тройки образуют абелеву группу[29].
Пифагоровы тройки на двумерной решётке[править | править код]
Двумерная решётка — это набор изолированных точек, в котором, если выбрать одну точку в качестве начала координат (0, 0), все другие точки имеют координаты (x, y), где x и y пробегают все положительные и отрицательные целые числа. Любую пифагорову тройку (a, b, c) можно нарисовать на двумерной решётке как точки с координатами (a, 0) и (0, b). По теореме Пика число точек решётки, лежащих строго внутри треугольника, задаётся формулой [30]. Для примитивных пифагоровых троек число точек решётки равно , и это сравнимо с площадью треугольника
Интересно, что первый случай совпадения площадей примитивных пифагоровых троек появляется на тройках (20, 21, 29), (12, 35, 37) с площадью 210[31]. Первое же появление примитивных пифагоровых троек с одинаковым числом точек решётки появляется лишь на (18 108, 252 685, 253 333), (28 077, 162 964, 165 365) с числом точек 2 287 674 594[32]. Найдены три примитивные пифагоровы тройки с одинаковыми площадями (4485, 5852, 7373), (3059, 8580, 9109), (1380, 19 019, 19 069) и площадью 13 123 110. Тем не менее ни одной тройки примитивных пифагоровых троек с одинаковым числом точек решётки пока не найдено.
Спиноры и модулярная группа[править | править код]
Пифагоровы тройки можно представить в виде матриц вида
Матрица этого вида симметрична. Кроме того, её определитель
равен нулю в точности тогда, когда (a, b, c) является пифагоровой тройкой. Если X соответствует пифагоровой тройке, то она должна иметь ранг 1.
Поскольку X симметрична, из линейной алгебры известно, что существует вектор ξ = [m n]T, такой, что для внешнего произведения выполняется
- (1)
где T означает транспонирование. Вектор ξ называется спинором (для группы Лоренца SO(1, 2). В абстрактных терминах формула Евклида означает, что каждая примитивная пифагорова тройка может быть записана как внешнее произведение на себя спинора с целыми элементами, как в формуле (1).
Модулярная группа Γ — это множество матриц 2 × 2 с целыми элементами
и определителем, равным единице: αδ − βγ = 1. Это множество образует группу, поскольку обратная к матрице из Γ является снова матрицей из Γ, как и произведение двух матриц из Γ. Модулярная группа действует на множество всех целых спиноров. Более того, группа транзитивна на множестве целых спиноров со взаимно простыми элементами. Если [m n]T содержит взаимно простые элементы, то
где u и v выбраны (с помощью алгоритма Евклида) так, что mu + nv = 1.
Действуя на спинор ξ в (1), действие в Γ переходит в действие над пифагоровыми тройками, позволяя при этом тройки с отрицательными значениями. Если A — матрица в Γ, то
- (2)
даёт начало действиям на матрицу X в (1). Это не даёт хорошо определённое действие на примитивные тройки, поскольку оно может переводить примитивную тройку в непримитивную. В этом месте принято (следуя Траутману[28]) называть тройку (a, b, c) стандартной, если c > 0 и либо (a, b, c) взаимно просты, либо (a/2, b/2, c/2) взаимно просты и a/2 нечётно. Если спинор [m n]T имеет взаимно простые элементы, то связанная тройка (a, b, c), задаваемая формулой (1), является стандартной тройкой. Отсюда следует, что действие модулярной группы транзитивно на множестве стандартных троек.
Альтернативно, ограничимся теми значениями m и n, для которых m нечётно, а n чётно. Пусть подгруппа Γ(2) группы Γ — ядро гомоморфизма
где SL(2, Z2) — специальная линейная группа над конечным полем Z2 целых по модулю 2. Тогда Γ(2) является группой унимодулярных преобразований, которая сохраняет чётность каждого элемента. Таким образом, если элемент вектора ξ нечётный, а второй чётный, то то же самое верно для Aξ для всех A ∈ Γ(2). Фактически под действием (2) группа Γ(2) действует транзитивно на множество примитивных пифагоровых троек[33].
Группа Γ(2) является свободной группой, генераторами которой являются матрицы
Поэтому любая примитивная пифагорова тройка может быть получена единственным образом как произведение копий матриц U и L.
Отношения «родитель — потомок»[править | править код]
Как показал Берггрен[34], все примитивные пифагоровы тройки могут быть получены из треугольника (3, 4, 5) с использованием трёх линейных преобразований T1, T2, T3, где a, b, c являются сторонами тройки:
| новая сторона a | новая сторона b | новая сторона c | |
| T1: | a − 2b + 2c | 2a − b + 2c | 2a − 2b + 3c |
| T2: | a + 2b + 2c | 2a + b + 2c | 2a + 2b + 3c |
| T3: | −a + 2b + 2c | −2a + b + 2c | −2a + 2b + 3c |
Если начать с 3, 4, 5, то все другие примитивные тройки, в конечном счёте, будут получены. Другими словами, любая примитивная тройка будет «родителем» 3 дополнительным примитивным тройкам. Если начать с a = 3, b = 4 и c = 5, то следующим поколением троек будет
| новая сторона a | новая сторона b | новая сторона c |
| 3 − (2×4) + (2×5) = 5 | (2×3) − 4 + (2×5) = 12 | (2×3) − (2×4) + (3×5) = 13 |
| 3 + (2×4) + (2×5) = 21 | (2×3) + 4 + (2×5) = 20 | (2×3) + (2×4) + (3×5) = 29 |
| −3 + (2×4) + (2×5) = 15 | −(2×3) + 4 + (2×5) = 8 | −(2×3) + (2×4) + (3×5) = 17 |
Линейные преобразования T1, T2 и T3 имеют геометрическую интерпретацию на языке квадратичных форм. Они тесно связаны (но не эквивалентны) с отражениями, генерируемыми ортогональной группой x2 + y2 − z2 над целыми числами. Другое множество трёх линейных преобразований обсуждается в статье Генерация пифагоровых троек с помощью матриц и линейных преобразований[35].
Связь с гауссовыми целыми числами[править | править код]
Формулы Евклида могут быть проанализированы и доказаны с помощью гауссовых целых чисел[36]. Гауссовы целые — это комплексные числа вида α = u + vi, где u и v обычные целые числа, а i — корень из минус единицы. Единицы гауссовых целых — это ±1 и ±i. Обычные целые называются целыми и обозначаются Z. Гауссовы целые обозначаются Z[i]. Правая часть теоремы Пифагора можно разложить на гауссовы целые:
Примитивная пифагорова тройка — это тройка, в которой a и b взаимно просты, то есть не имеют общих простых делителей. Для таких троек либо a, либо b чётно, а второе нечётно. Отсюда следует, что c также нечётно.
Каждый из двух множителей z = a + bi и z* = a — bi примитивной пифагоровой тройки равен квадрату гауссового целого. Это можно доказать с помощью свойства, что любое гауссово целое можно единственным образом разложить на гауссовы простые с точностью до единицы[37]. (Единственность разложения, грубо говоря, следует из того, что для них можно определить версию алгоритма Евклида) Доказательство имеет три шага. Сначала доказывается, что если a и b не имеют простых чисел в целых числах, то они не имеют простых общих множителей в гауссовых целых. Отсюда следует, что z и z* не имеют общих простых множителей в гауссовых целых. И наконец, поскольку c2 является квадратом, любое гауссово простое в разложении повторяется дважды. Поскольку z и z* не имеют общих простых множителей, это удвоение верно и для них. Следовательно, z и z* являются квадратами.
Таким образом, первый множитель можно записать в виде
Вещественные и мнимые части этого уравнения дают две формулы:
Для любой примитивной пифагоровой тройки должны существовать целые m и n, такие что эти два равенства выполняются. Отсюда, любая пифагорова тройка может быть получена путём выбора этих целых.
Как полный квадрат гауссовых целых[править | править код]
Если взять квадрат гауссового целого, мы получим следующую интерпретацию формул Евклида как представление полного квадрата гауссовых целых.
Если использовать факт, что гауссовы целые являются евклидовой областью и то, что для гауссовых целых p квадрат модуля всегда является полным квадратом, можно показать, что пифагоровы тройки соответствуют квадратам простых гауссовых целых, если гипотенуза является простым числом.
Распределение троек[править | править код]
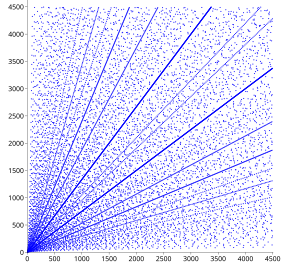
Имеется множество результатов относительно распределения пифагоровых троек. В диаграмме рассеяния проявляются некоторые очевидные закономерности. Если катеты (a, b) примитивной тройки появляются на диаграмме, то и все произведения на целое число этих катетов должны также быть на диаграмме, и это свойство объясняет появление на диаграмме радиальных прямых из начала координат.
На диаграмме наблюдаются множества парабол с высокой плотностью точек, имеющих фокусы в начале координат. Параболы отражаются от осей с углом 45 градусов, и в той же точке третья парабола подходит к оси перпендикулярно.
Эти узоры можно объяснить следующим образом. Если натуральное число, то (a, , ) является пифагоровой тройкой. (Фактически, любая пифагорова тройка (a, b, c) может быть записана таким образом с целым n, возможно, после обмена a и b местами, поскольку и a, b не могут быть одновременно нечётными.) Пифагоровы тройки лежат тогда на кривых, заданных уравнениями . Таким образом, параболы отражаются от оси a, а соответствующие кривые с a и b меняются местами. Если a меняется при заданном n (то есть на выбранной параболе), целые значения b появляются относительно часто, если n является квадратом или произведением квадрата на небольшое число. Если некоторые такие значения лежат близко друг от друга, соответствующие параболы почти совпадают и тройки образуют узкую параболическую ленту. Например, 382 = 1444, 2 × 272 = 1458, 3 × 222 = 1452, 5 × 172 = 1445 и 10 × 122 = 1440. Соответствующая параболическая лента около n ≈ 1450 чётко видна на диаграмме рассеяния.
Угловые свойства, описанные выше следуют немедленно из функционального вида парабол. Параболы отражаются от оси a в точке a = 2n и производная b по a в этой точке равна −1. Таким образом, угол наклона равен 45°. Поскольку кластеры, как и треугольники, повторяются при умножении на целую константу, значение 2n тоже принадлежит кластеру. Соответствующая парабола пересекает ось b под прямым углом в точке b = 2n, а потому является симметричным отражением параболы, которая получается обменом переменных a и b и которая пересекает ось a под прямым углом в точке a = 2n.
Альберт Фесслер (Albert Fässler) и др. показали значимость этих парабол в контексте конформных отображений[38][39].
Специальные случаи[править | править код]
Последовательность Платона[править | править код]
Случай n = 1 общей конструкции пифагоровых троек известен давно. Прокл, в своём комментарии к 47-му утверждению в первой книге Начал Евклида, описывает это следующим образом:
Некоторые методы получения таких треугольников этого вида легко получить, один из них принадлежит Платону, другой — Пифагору. (Последний) начал с нечётных чисел. Для этого он выбрал нечётное число в качестве меньшего из катетов. Затем он возвёл его в квадрат, вычел единицу и половину этой разницы использовал как второй катет. Наконец, он добавил единицу к этому катету и получил гипотенузу.
…Метод Платона работает с чётными числами. Он использует заданное чётное число в качестве одного из катетов. Половина этого числа возводится в квадрат и добавляется единица, что даёт гипотенузу, а вычитание единицы даёт второй катет. … И это даёт тот же треугольник, что и другой метод.
В виде уравнений:
- a нечётно (Пифагор, 540 до н. э.):
- a чётно (Платон, 380 до н. э.):
Можно показать, что все пифагоровы тройки получаются из последовательности Платона (x, y, z) = p, (p2 − 1)/2 и (p2 + 1)/2, если позволить p принимать нецелые (рациональные) значения. Если в этой последовательности p заменить рациональной дробью m/n, получим 'стандартный' генератор троек 2mn, m2 − n2 и m2 + n2. Отсюда следует, что любой тройке соответствует рациональное значение p, которое можно использовать для получения подобного треугольника с рациональными сторонами, пропорциональными сторонам исходного треугольника. Например, платоновым эквивалентом тройке (6, 8, 10) будет (3/2; 2, 5/2).
Уравнение Якоби — Маддена[править | править код]
Уравнение
эквивалентно специальной диофантовой тройке
Существует бесконечное число решений этого уравнения, которые можно получить используя эллиптическую кривую. Два из этих решений:
Равные суммы двух квадратов[править | править код]
Один из способов генерации решений для — параметризовать a, b, c, d в терминах натуральных чисел m, n, p, q следующим образом:[40]
Равные суммы двух четвёртых степеней[править | править код]
Если даны два набора пифагоровых троек:
то задача поиска равных произведений катета и гипотенузы
как легко видеть, эквивалентна уравнению
то есть
для которого Эйлер получил решение . Поскольку он показал, что эта точка является рациональной точкой эллиптической кривой, то существует бесконечное число решений. Фактически, он также нашёл полиномиальную параметризацию 7-й степени.
Теорема Декарта об окружностях[править | править код]
В случае теоремы Декарта, когда все переменные являются квадратами,
Эйлер показал, что это эквивалентно трём пифагоровым тройкам:
Здесь тоже существует бесконечное число решений, а для специального случая уравнение упрощается до
которое имеет решение с небольшими числами и может быть решено как бинарная квадратичная форма.
Почти равнобедренные пифагоровы тройки[править | править код]
Имеются прямоугольные треугольники с целыми сторонами, у которых длины катетов отличаются на единицу, например:
и бесконечное число других. Для них можно вывести общую формулу
где (x, y) являются решениями уравнения Пелля .
В случае, когда катет и гипотенуза отличаются на единицу, как в случаях
общим решением будет
откуда видно, что все нечётные числа (большие 1) появляются в примитивных пифагоровых тройках.
Обобщения[править | править код]
Имеется несколько вариантов обобщения концепции пифагоровых троек.
Пифагоровы четвёрки[править | править код]
Множество из четырёх натуральных чисел a, b, c и d, таких, что a2 + b2+ c2 = d2 называется пифагоровой четвёркой. Простейший пример — (1, 2, 2, 3), поскольку 12 + 22 + 22 = 32. Следующий (примитивный) простейший пример — (2, 3, 6, 7), поскольку 22 + 32 + 62 = 72.
Все четвёрки задаются формулой
Пифагоровы n-наборы[править | править код]
Используя простое алгебраическое тождество
для произвольных x0, x1, просто доказать, что квадрат суммы n квадратов сам является суммой n квадратов, для чего положим x0 = x22 + x32 + … + xn2 и раскроем скобки[41]. Можно легко видеть, что пифагоровы тройки и четвёрки являются просто частными случаями x0 = x22 и x0 = x22 + x32 соответственно, что можно продолжать для других n, используя формулу для пятёрки квадратов
Поскольку сумма F(k,m) k последовательных квадратов, начиная с m2, задаётся формулой[42]
можно найти значения (k, m) такие, что F(k,m) является квадратом. Так, Хиршхорн нашёл формулу для последовательностей, в которых число членов само является квадратом[43],
и v ⩾ 5 есть любое натуральное число, не делящееся на 2 или 3. Наименьшее значение v = 5, откуда k = 25, что даёт хорошо известное значение из задачи Люка складирования пушечных ядер:
факт, который связан с решёткой Лича.
Кроме того, если в пифагоровом n-наборе (n ⩾ 4) все слагаемые являются последовательными натуральными числами, за исключением последнего, можно использовать равенство[44]
Поскольку вторая степень p сокращается, остаётся линейное уравнение, которое легко решается , хотя k и m следует выбрать так, чтобы p был целым, и пример получаем при k = 5 и m = 1:
Таким образом, получаем метод генерации пифагоровых n-наборов путём подбора x[45]:
где q = n − 2 и
Великая теорема Ферма[править | править код]
Обобщением концепции пифагоровых троек служит поиск троек натуральных чисел a, b и c, таких, что an + bn = cn для некоторого n, большего 2. Пьер Ферма в 1637 году высказал утверждение, что таких троек не существует, и это утверждение стало известно как Великая теорема Ферма, поскольку её доказательство или опровержение отняло много больше времени, чем любая другая гипотеза Ферма. Первое доказательство было дано Уайлсом в 1994 году.
n — 1 или n n-х степеней как n-я степень[править | править код]
Другим обобщением является поиск последовательностей из n + 1 натуральных чисел, для которых n-я степень последнего члена последовательности равна сумме n-х степеней предыдущих членов. Наименьшие последовательности для известных значений n:
- n = 3: {3, 4, 5; 6}.
- n = 4: {30, 120, 272, 315; 353}
- n = 5: {19, 43, 46, 47, 67; 72}
- n = 7: {127, 258, 266, 413, 430, 439, 525; 568}
- n = 8: {90, 223, 478, 524, 748, 1088, 1190, 1324; 1409}
В слегка отличном обобщении сумма (k + 1) n-х степеней приравнивается сумме (n − k) n-х степеней. Например:
- (n = 3): 13 + 123 = 93 + 103. Пример стал известным после воспоминаний Харди о разговоре с Рамануджаном о числе 1729, которое является наименьшим числом, которое можно представить в виде суммы двух кубов двумя различными способами.
Может существовать также n − 1 n-х степеней натуральных чисел, дающих в сумме n-ю степень натурального числа (хотя, согласно великой теореме Ферма, не для n = 3). Эти последовательности являются контрпримерами гипотезе Эйлера. Наименьшие известные контрпримеры[46][47]
- n = 4: (95800, 217519, 414560; 422481)
- n = 5: (27, 84, 110, 133; 144)
Тройки треугольника Герона[править | править код]
Треугольник Герона обычно определяется как треугольник с целыми сторонами, площадь которого тоже целое число, и мы будем полагать, что стороны треугольника различны. Длины сторон такого треугольника образуют тройку Герона (a, b, c), где a < b < c. Ясно, что пифагоровы тройки являются тройками Герона, поскольку в пифагоровой тройке по меньшей мере один из катетов a и b является чётным числом, так что площадь треугольника ab/2 будет целым числом. Не всякая тройка Герона является пифагоровой, поскольку, например, тройка (4, 13, 15) с площадью 24 не пифагорова.
Если (a, b, c) является тройкой Герона, то таковой будет и (ma, mb, mc) при любом натуральном m, большим единицы. Тройка Герона (a, b, c) примитивна, если a, b и c попарно взаимно просты (как и в случае пифагоровых троек). Ниже приведено несколько троек Герона, не являющихся пифагоровыми:
- (4, 13, 15) с площадью 24,
- (3, 25, 26) с площадью 36,
- (7, 15, 20) с площадью 42,
- (6, 25, 29) с площадью 60,
- (11, 13, 20) с площадью 66,
- (13, 14, 15) с площадью 84,
- (13, 20, 21) с площадью 126.
По формуле Герона, чтобы тройка натуральных чисел (a, b, c) с a < b < c была тройкой Герона, необходимо, чтобы
- (a2 + b2 + c2)2 − 2 (a4 + b4 + c4)
или, что то же самое,
- 2 (a2b2 + a2c2 + b2c2) − (a4 + b4 + c4)
было ненулевым полным квадратом, делящимся на 16.
Использование[править | править код]
Примитивные пифагоровы тройки используются в криптографии в качестве случайных последовательностей и для генерации ключей[48].
См. также[править | править код]
- Геронов треугольник
- Диофант II.VIII
- Египетский треугольник
- Негипотенузное число
- Пифагорова четвёрка
- Простое число Пифагора
- Прямоугольный треугольник
- Сравнение по модулю
- Совершенный кубоид
- Теорема Пифагора
- Теорема Гильберта 90
- Теорема Ферма о прямоугольном треугольнике
- Тригонометрические тождества
- Тройка Эйзенштейна
- Формула тангенса половинного угла
- Целочисленный треугольник
Примечания[править | править код]
- ↑ В. Серпинский. Пифагоровы треугольники. — М.: Учпедгиз, 1959. — 111 с.
- ↑ Robson, Eleanor (February 2002), "Words and pictures: new light on Plimpton 322" (PDF), American Mathematical Monthly, Mathematical Association of America, 109 (2): 105—120, doi:10.2307/2695324, JSTOR 2695324, MR 1903149 Архивная копия от 10 августа 2017 на Wayback Machine
- ↑ D. E. Joyce. Euclid's Elements. — Clark University, June 1997. — С. Book X, Proposition XXIX.
- ↑ Douglas W. Mitchell. An Alternative Characterisation of All Primitive Pythagorean Triples // The Mathematical Gazette. — July 2001. — Т. 85, вып. 503. — С. 273–5. — .
- ↑ Raymond A. Beauregard, E. R. Suryanarayan. Proofs Without Words: More Exercises in Visual Thinking / Roger B. Nelsen. — Mathematical Association of America, 2000. — Т. II. — С. 120. — ISBN 978-0-88385-721-2.
- ↑ Eli Maor. The Pythagorean Theorem. — Princeton University Press, 2007. — С. Appendix B.
- ↑ 1 2 3 Sierpinski, 2003.
- ↑ Houston, 1993, с. 141.
- ↑ Posamentier, 2010, с. 156.
- ↑ Несуществование решения, в котором и a, и b являются квадратами, первоначально доказано Пьером Ферма. Для других случаев, в которых c является одним из квадратов, см. в книге Стиллвела.
- ↑ Carmichael, 1959, с. 17.
- ↑ Carmichael, 1959, с. 21.
- ↑ Sierpinski, 2003, с. 4—6.
- ↑ Sierpinski, 2003, с. 23—25.
- ↑ MacHale, Bosch, 2012, с. 91—96.
- ↑ Sally, 2007, с. 74—75.
- ↑ Это следует из факта, что одно из чисел a или b делится на четыре, и из определения конгруэнтных чисел как площадей прямоугольных треугольников с рациональными сторонами
- ↑ Baragar, 2001, с. 301, упражнение 15.3.
- ↑ Bernhart, Price, 2005.
- ↑ Bernhart, Price, 2005, с. 6.
- ↑ Carmichael, 1959, с. 14.
- ↑ Rosenberg, Spillane, Wulf, May 2008, с. 656—663.
- ↑ Paul Yiu, 2008.
- ↑ Sierpinski, 2003, с. 31.
- ↑ Pickover, 2009, с. 40.
- ↑ Paul Yiu, 2008, с. 17.
- ↑ Weisstein, Eric W. Пифагорова тройка (англ.) на сайте Wolfram MathWorld.
- ↑ 1 2 Trautman, 1998.
- ↑ Eckert, 1984.
- ↑ Paul Yiu, 2003.
- ↑ Последовательность A093536 в OEIS.
- ↑ Последовательность A225760 в OEIS.
- ↑ Alperin, 2005.
- ↑ Berggren, 1934.
- ↑ Дальнейшее обсуждение отношения «родитель — потомок» — Pythagorean triple (Wolfram) Архивная копия от 17 марта 2015 на Wayback Machine, Alperin, 2005.
- ↑ Stillwell, 2002, с. 110–2 Глава 6.6 Pythagorean Triples.
- ↑ Gauss, 1832 См. также Werke, 2:67-148.
- ↑ 1988 Preprint Архивная копия от 9 августа 2011 на Wayback Machine См. рисунок 2 на с. 3. Позднее это было напечатано в (Fässler 1991)
- ↑ Benito, Varona, 2002, с. 117–126.
- ↑ Nahin, Paul. An Imaginary Tale: The Story of p. 25—26.
- ↑ A Collection of Algebraic Identities: Sums of n Squares. Дата обращения: 15 марта 2015. Архивировано 6 марта 2012 года.
- ↑ Sum of consecutive cubes equal a cube. Архивировано из оригинала 15 мая 2008 года.
- ↑ Michael Hirschhorn. When is the sum of consecutive squares a square? // The Mathematical Gazette. — November 2011. — Т. 95. — С. 511–2. — ISSN 0025-5572.
- ↑ John F. Jr. Goehl. Reader reflections // Mathematics Teacher. — May 2005. — Т. 98, вып. 9. — С. 580.
- ↑ John F. Goehl, Jr. Triples, quartets, pentads // Mathematics Teacher. — May 2005. — Т. 98. — С. 580.
- ↑ Scott Kim. Bogglers // Discover. — May 2002. — С. 82.
Уравнение сложнее, лишь в 1988 году после 200 лет безуспешных попыток математиков доказать невозможность решить уравнение Ноам Элкис из Гарварда нашёл контрпример — 2.682.4404 + 15.365.6394 + 18.796.7604 = 20.615.6734:
- Noam Elkies. On A4 + B4 + C4 = D4 // Mathematics of Computation. — 1988. — Т. 51. — С. 825–835.
- ↑ MacHale, Bosch, 2012, с. 91-96.
- ↑ S. Kak, M. Prabhu. Cryptographic applications of primitive Pythagorean triples // Cryptologia. — 2014. — Т. 38, вып. 3. — С. 215-222.
Литература[править | править код]
- R. D. Carmichael. The Theory of Numbers and Diophantine Analysis. — Dover Publ, 1959. — С. Diophantine analysis.
- Waclaw Sierpinski. Pythagorean Triangles. — Dover, 2003. — ISBN 978-0-486-43278-6.
- John Stillwell. Numbers and Geometry. — Springer, 1998. — С. 133. — (Undergraduate Texts in Mathematics). — ISBN 9780387982892.
- Thomas Koshy. Elementary Number Theory with Applications. — Academic Press, 2002. — С. 545. — ISBN 9780124211711.
- David Houston. Proofs Without Words: Exercises in Visual Thinking / Roger B. Nelsen. — Mathematical Association of America, 1993. — С. 141. — ISBN 978-0-88385-700-7.
- Alfred S. Posamentier. The Pythagorean Theorem: The Story of Its Power and Beauty. — Prometheus Books, 2010. — ISBN 9781616141813.
- Des MacHale, Christian van den Bosch. Generalising a result about Pythagorean triples // Mathematical Gazette. — 2012. — Т. 96.
- Judith D. Sally. Roots to Research: A Vertical Development of Mathematical Problems. — American Mathematical Society, 2007. — ISBN 9780821872673..
- Neal Koblitz. Introduction to Elliptic Curves and Modular Forms. — Springer, 1993. — Т. 97. — (Graduate Texts in Mathematics). — ISBN 9780387979663.
- Arthur Baragar. A Survey of Classical and Modern Geometries: With Computer Activities. — Prentice Hall, 2001. — ISBN 9780130143181.
- Paul Yiu. Heron triangles which cannot be decomposed into two integer right triangles. — 41st Meeting of Florida Section of Mathematical Association of America, 2008.
- Clifford A. Pickover. The Math Book. — Sterling, 2009. — С. Глава «Pythagorean Theorem and Triangles». — ISBN 1402757964.
- John Stillwell. Elements of Number Theory. — Springer, 2002. — ISBN 978-0-387-95587-2.
- Pythagorean Triples and the Unit Circle Архивная копия от 15 декабря 2011 на Wayback Machine, chap. 2-3, in «A Friendly Introduction to Number Theory Архивная копия от 6 марта 2015 на Wayback Machine» by Joseph H. Silverman, 3rd ed., 2006, Pearson Prentice Hall, Upper Saddle River, NJ, ISBN 0-13-186137-9
- Дмитрий Викторович Аносов. Взгляд на математику и нечто из неё. — 2-е изд. — М.: МЦНМО, 2003. — Т. 3. — 32 с. — (Библиотека «Математическое просвещение»). — 3000+1500 экз. — ISBN 5-94057-111-5. Архивировано 12 января 2014 года. Архивная копия от 12 января 2014 на Wayback Machine
Ссылки[править | править код]
- Paul Yiu. Recreational Mathematics // Course Notes, Dept. of Mathematical Sciences, Florida Atlantic University. — 2003.
- Frank R. Bernhart, H. Lee Price. Heron's formula, Descartes circles, and Pythagorean triangles. — 2005. arXiv
- Steven Rosenberg, Michael Spillane, Daniel B. Wulf. Heron triangles and moduli spaces // Mathematics Teacher. — May 2008. — Т. 101.
- Gauss C. F. Theoria residuorum biquadraticorum // Comm. Soc. Reg. Sci. Gött. Rec.. — 1832. — Т. 4.
- Albert Fässler. Multiple Pythagorean number triples // American Mathematical Monthly. — 1991. — Т. 98, вып. 6. — .
- Manuel Benito, Juan L. Varona. Pythagorean triangles with legs less than n. — 2002. — Т. 143. — doi:10.1016/S0377-0427(01)00496-4.
- Roger C. Alperin. The modular tree of Pythagoras // American Mathematical Monthly. — Mathematical Association of America, 2005. — Т. 112, вып. 9. — С. 807–816. — .
- B. Berggren. Pytagoreiska trianglar (швед.) // Tidskrift för elementär matematik, fysik och kemi. — 1934. — Т. 17. — С. 129–139.
- Ernest Eckert. Primitive Pythagorean triples // The College Mathematics Journal. — Mathematical Association of America, 1992. — Т. 23, вып. 5. — С. 413–417. — .
- Ernest J. Eckert, Preben Dahl Vesrergaard. Groups of integral triangles // The Fibonacci Quarterly. — 1989. — Т. 27, вып. 5. — С. 458—464.
- Ernest J. Eckert. The Group of Primitive Pythagorean Triangles // Mathematics Magazine. — 1984. — Т. 57.
- Noam Elkies. Pythagorean triples and Hilbert's theorem 90.
- Artemas Martin. Rational right angled triangles nearly isosceles // The Analyst. — Annals of Mathematics, 1875. — Т. 3, вып. 2. — С. 47–50. — doi:10.2307/2635906. — .
- Andrzej Trautman. Geometric universe / S. A. Hugget, L. J. Mason, K. P. Tod, S. T. Tsou, N. M. J. Woodhouse. — 1998.
- Weisstein, Eric W. Pythagorean Triple (англ.) на сайте Wolfram MathWorld.
Для улучшения этой статьи желательно:
|
































































![{\displaystyle [(a-1)(b-1)-\gcd(a,b)+1]/2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6cf82ec50d495b3453d2df1b107e026a5f88670e)




























































