Многочлен

Многочле́н (или полино́м, от греч. πολυ- «много» + лат. nomen «имя»[1]) — фундаментальное понятие в алгебре и математическом анализе. В простейшем случае многочленом называется функция вещественной или комплексной переменной следующего вида[2]:
- , где — фиксированные коэффициенты, причём .
Максимальная степень среди слагаемых-одночленов называется степенью многочлена. Если нет ни одного слагаемого, то такой многочлен называется нуль-многочленом, его степень точно не определена, но при этом считается меньшей любого неотрицательного числа.
Примеры:
- (многочлен второй степени)
- (многочлен пятой степени)
В более общем случае многочлен может содержать степени нескольких независимых переменных[3] например:
- Это многочлен от двух переменных второй степени.
Многочлены как функции можно складывать, перемножать, а в некоторых случая и делить один на другой[4]
Коэффициенты многочлена могут быть не обязательно числовыми.
Многочлены от одной переменной[править | править код]
В этом разделе, если не оговорено иное, под многочленом всюду понимается многочлен от одной переменной.
- Графики многочленов разной степени
-
Многочлен 1-й степени
f(x) = 2x + 1 -
Многочлен 2-й степени
f(x) = x2 − x − 2
= (x + 1)(x − 2) -
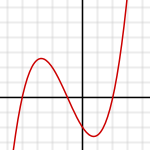
Многочлен 3-й степени
f(x) = x3/4 + 3x2/4 − 3x/2 − 2
= 1/4 (x + 4)(x + 1)(x − 2)
Основные понятия[править | править код]
Общий вид многочлена[2] от одной переменной :
- ,
где — фиксированные числовые коэффициенты, причём .
Таким образом, многочлен есть сумма одночленов разных степеней. Максимальная степень среди слагаемых-одночленов называется степенью многочлена, а коэффициент при этом одночлене называется старшим коэффициентом[5]. Степень произведения многочленов равна сумме степеней сомножителей. Одночлен , не содержащий переменной, называется свободным членом многочлена.
Допускается многочлен, вообще не содержащий переменных, то есть числовая константа: ; его степень считается равной нулю. Исключением является нулевой многочлен, тождественно равный нулю: , его степень не определяется (иногда считается равной или )[6], но в любом случае считается меньшей степени любого другого многочлена. В частности, это означает, что констатные многочлены это в точности многочлены степени не выше 0.
Некоторые классы многочленов имеют специальные названия[3][5].
- Многочлен первой степени называется линейным двучленом или биномом.
- Многочлен второй степени из трёх членов называется квадратным трёхчленом.
- Многочлен третьей степени называется кубическим.
- Многочлен называется приведённым (также нормированным или унитарным), если его старший коэффициент равен единице.
Деление многочленов[править | править код]
Определение[7]: говорят, что многочлен делится (нацело) на многочлен , если существует такой многочлен , что .
Как и при делении целых чисел, , и называются делимым, делителем и частным соответственно.
Основные свойства деления многочленов (вполне аналогичные свойствам деления целых чисел)[7].
- Транзитивность: если делится на и делится на , то делится на .
- Частное от деления на также является делителем .
- Если оба многочлена делятся на , то их сумма и разность также делится на .
- Если делится на , то его произведение на любой другой многочлен также делится на .
- Степень частного равна разности степеней делимого и делителя.
- Всякий многочлен делится на любой многочлен нулевой степени (то есть на ненулевое число).
- Многочлены и делятся друг на друга тогда и только тогда, когда , где — ненулевая константа.
Как и для целых чисел, можно определить понятие наибольшего общего делителя (НОД) двух многочленов и — это многочлен, который является делителем \как , так и и при этом делится на любой другой общий делитель этих многочленов. НОД всегда существует и определён с точностью до числового множителя. Если степень НОД равна нулю (то есть это число), многочлены и называются взаимно простыми[7]. Для нахождения НОД можно использовать аналог алгоритма Евклида[8].
Деление с остатком[править | править код]
Любой многочлен можно разделить на ненулевой многочлен меньшей степени с остатком, то есть представить его в виде:
где степень R(x) (многочлена-остатка) меньше, чем степень делителя . Многочлен называется неполным частным. Многочлены и для заданных , определены однозначно[3].
Пример: остаток от деления многочлена на равен :
Теорема Безу: остаток от деления многочлена на двучлен равен .
Корни многочлена[править | править код]
Решения уравнения называются корнями (ненулевого) многочлена .
Свойства:
- Коэффициенты многочлена связаны с его корнями формулами Виета[9].
- (Основная теорема алгебры): всякий отличный от константы многочлен (от одной переменной) с вещественными или комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел[10].
- Всякий отличный от константы многочлен с вещественными коэффициентами может быть разложен в произведение[11]:
- — своего старшего коэффициента ;
- — нескольких линейных двучленов вида где — вещественные корни , если они существуют;
- — нескольких приведённых квадратных трёхчленов, соответствующих парам сопряжённых комплексных корней , если они существуют.
- Это разложение однозначно с точностью до порядка сомножителей.
Пример:
Здесь первая скобка справа соответствует вещественному корню а вторая — паре сопряжённых комплексных корней .
Приводимость и каноническое разложение многочлена[править | править код]
Многочлен называется приводимым, если он является произведением двух многочленов положительных степеней, и неприводимым — в противном случае.
Любой многочлен, кроме нуль-многочлена, над любым полем имеет каноническое разложение в произведение неприводимых множителей, которое однозначно с точностью до порядка сомножителей и константных множителей. При этом кратное повторение одного или более сомножителей с точностью до константных множителей имеет место в точности тогда, когда многочлен не является взаимно простым со своей производной.
Многочлены от нескольких переменных[править | править код]
Многочлен от нескольких переменных — это конечная сумма одночленов вида[12]::
- ,
Далее предполагается, что все подобные одночлены объединены, и все коэффициенты при одночленах ненулевые.
Степенью каждого одночлена называется сумма степеней входящих в него переменных, а максимальная степень среди слагаемых-одночленов называется степенью многочлена от нескольких переменных. Коэффициент при этом одночлене называется старшим коэффициентом. Очевидно, степень произведения многочленов равна сумме степеней сомножителей[11].
Одночлен, не содержащий переменных, называется свободным членом многочлена.
Многочлен, все члены которого имеют одну и ту же степень, называется однородным многочленом. или формой (линейной, квадратичной, кубической и т. д., в зависимости от степени). Например, — однородный многочлен двух переменных, а не является однородным.
Изучение и применение[править | править код]

Изучение полиномиальных уравнений и их решений долгое время составляло едва ли не главный объект «классической алгебры».
С изучением многочленов исторически связан целый ряд преобразований в математике: введение в рассмотрение нуля, отрицательных, а затем и комплексных чисел, а также появление теории групп как раздела математики и выделение классов специальных функций в математическом анализе. С помощью многочлена вводятся понятия «алгебраическое уравнение», «алгебраическая функция» и «алгебраическое число».
Одно из важнейших применений алгебры многочленов связано с тем, что любую непрерывную функцию можно с произвольно малой ошибкой заменить на многочлен (теорема Вейерштрасса). Это позволяет приближённо выражать многочленами широкие классы функций [3].
Многочлены также играют ключевую роль в алгебраической геометрии. Её ключевым объектом являются множества, определённые как решения систем полиномиальных уравнений.
Особые свойства преобразования коэффициентов при перемножении многочленов используются в алгебраической геометрии, алгебре, теории узлов и других разделах математики для кодирования или выражения при помощи многочленов свойств различных объектов.
Вариации и обобщения[править | править код]
Кольцо многочленов[править | править код]
Коэффициенты многочлена обычно берутся из определённого коммутативного кольца (чаще всего поля, например, поля вещественных или комплексных чисел). В этом случае относительно операций сложения и умножения многочлены образуют кольцо (более того ассоциативно-коммутативную алгебру над кольцом без делителей нуля), которое обозначается .
Понятие многочлена можно определить для произвольного поля, даже нечислового. Множество всех многочленов с коэффициентами из данного поля образует кольцо — кольцо многочленов над данным полем; это кольцо не имеет делителей нуля, то есть произведение ненулевых многочленов не может дать нулевой многочлен[3].
Многочлен, который можно представить в виде произведения многочленов низших степеней с коэффициентами из того же поля, называется приводимым (над данным полем), в противном случае — неприводимым.
Кольцо многочленов над произвольной областью целостности само является областью целостности.
Кольцо многочленов от любого конечного числа переменных над любым факториальным кольцом само является факториальным.
Роль неприводимых многочленов в кольце многочленов сходна с ролью простых чисел в кольце целых чисел. Например, верна теорема: если произведение многочленов делится на неприводимый многочлен , то p или q делится на . Каждый многочлен степени большей нуля разлагается в данном поле в произведение неприводимых множителей единственным образом (с точностью до множителей нулевой степени).
Например, многочлен , неприводимый в поле рациональных чисел, разлагается на три множителя в поле вещественных чисел и на четыре множителя в поле комплексных чисел.
Вообще, каждый многочлен от одного переменного разлагается в поле вещественных чисел на множители первой и второй степени, в поле комплексных чисел — на множители первой степени (основная теорема алгебры).
Для двух и большего числа переменных этого уже нельзя утверждать. Над любым полем для любого существуют многочлены от переменных, неприводимые в любом расширении этого поля. Такие многочлены называются абсолютно неприводимыми.
Кольцо многочленов от одного переменного над полем является кольцом главных идеалов, то есть любой его идеал может быть порождён одним элементом. Более того, кольцо многочленов от одного переменного над полем является евклидовым кольцом.
Если в определении допустить также отрицательные степени переменных, то полученный объект называется Многочлен Лорана.
Полиномиальная функция[править | править код]
Пусть — алгебра над кольцом Произвольный многочлен определяет полиномиальную функцию
Чаще всего рассматривают случай
В случае, если — поле вещественных или комплексных чисел (или любое другое поле с бесконечным числом элементов), функция полностью определяет многочлен p. Однако в общем случае это неверно, например: многочлены и из определяют тождественно равные функции .
Полиномиальная функция одного действительного переменного называется целой рациональной функцией.
См. также[править | править код]
- Базис Грёбнера
- Квазимногочлен
- Позином
- Сплайн
- Степенной ряд
- Теорема Гаусса — Люка
- Теорема о рациональных корнях.
- Тригонометрический многочлен
Примечания[править | править код]
- ↑ Полином // Советский энциклопедический словарь. — 2-е изд.. — М.: Советская энциклопедия, 1982. — 1600 с.
- ↑ 1 2 Винберг, 1980, с. 5.
- ↑ 1 2 3 4 5 БРЭ.
- ↑ Курош, 1968, с. 130—135.
- ↑ 1 2 Цыпкин, 1983, с. 88.
- ↑ Eric W. Weisstein. Zero Polynomial (англ.). mathworld.wolfram.com. Дата обращения: 28 мая 2021. Архивировано 1 мая 2021 года.
- ↑ 1 2 3 Цыпкин, 1983, с. 90—91.
- ↑ Цыпкин, 1983, с. 93—94.
- ↑ Курош, 1968, с. 158—159.
- ↑ Алгебры основная теорема // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1977. — Т. 1. — С. 199—200.
- ↑ 1 2 Цыпкин, 1983, с. 97—99.
- ↑ Цыпкин, 1983, с. 97—98.
Литература[править | править код]
- Винберг Э. Б. Алгебра многочленов. — М.: Просвещение, 1980. — 176 с.
- Курош А. Г. Курс высшей алгебры. — 9-е изд. — М.: Наука, 1968.
- Мишина А. П., Проскуряков И. В. Высшая алгебра, 2 изд. — М., 1965.
- Прасолов В. В. Многочлены. — 3-е изд. — М.: МЦНМО, 2003. — 336 с. — ISBN 5-94057-077-1.
- Солодовников А. С, Родина М. А. Задачник-практикум по алгебре. — М.: Просвещение, 1985. — 127 с.
- Фаддеев Д. К., Соминский И. С. Сборник задач по высшей алгебре. — М., 1977.
- Цыпкин А. Г. Справочник по математике для средних учебных заведений. — 3-е изд.. — М.: Наука, 1983. — 480 с.
Ссылки[править | править код]
- Многочлен / Маркушевич А. И. // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
















































![{\displaystyle R[x_{1},x_{2},\dots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7de1d5767a8f5ee8e1b21bad9b0a1b973342f0d3)






![{\displaystyle p(x)\in R[x_{1},x_{2},\dots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dbf310f3b74402f723c651e305773f1ede79f70)





![{\displaystyle \mathbb {Z} _{2}[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/212e1c6d785d21ce349483e42addda9718f55746)
