Барицентр

В математике барице́нтр, или геометри́ческий центр, двумерной фигуры — это среднее арифметическое положений всех точек данной фигуры. Определение распространяется на любой объект в n-мерном пространстве. Радиус-вектор барицентра в трёхмерном случае вычисляется как
- ,
где интегрирование выполняется по объёму тела. Другое название барицентра в этом значении — центроид.
Неформально, геометрический барицентр есть точка равновесия фигуры, вырезанной из картона, в предположении, что картон имеет постоянную плотность, а внешнее гравитационное поле однородно.
В физике термин «барицентр» — синоним понятия «центр масс», используемый, в основном, в задачах космической механики. Центр масс объекта является средним арифметическим всех его точек с учётом локальной плотности массы. Для физических объектов с постоянной плотностью центр масс совпадает с барицентром фигуры той же формы.
Ниже барицентр рассматривается в математическом (геометрическом) смысле, о барицентре в физике см. статью Центр масс.
Свойства[править | править код]
Геометрический барицентр выпуклого объекта всегда лежит внутри объекта. Невыпуклый объект может иметь барицентр, лежащий вне фигуры. Барицентр кольца или миски, например, лежат вне фигуры.
Если барицентр известен, он является фиксированной точкой группы изометрии симметрий фигуры. Барицентр объекта лежит на пересечении всех его гиперплоскостей симметрии. Барицентры многих фигур (правильного многоугольника, правильного многогранника, цилиндра, прямоугольника, ромба, окружности, сферы, эллипса, эллипсоида, суперэллипса, суперэллипсоида и т. д.) можно найти исходя исключительно из этого принципа.
В частности, барицентром треугольника является точка пересечения его медиан (см. рисунок). Барицентром параллелограмма является точка пересечения его диагоналей, но это неверно для других четырёхугольников.
Барицентр объекта с трансляционной симметрией не определён (или лежит вне пространства фигуры), поскольку сдвиг не имеет фиксированной точки.
Центроид треугольника[править | править код]
- Барицентр треугольника называется центроидом и лежит на пересечении трёх медиан, также лежит на прямой Эйлера (проходящей и через другие ключевые точки, включая ортоцентр и центр описанной окружности)[1][2].
- Если в вершины треугольника поместить равные массы, то центр масс (барицентр) полученной системы будет совпадать с центроидом. Более того, центр масс треугольника с равномерно распределённой массой также находится в центроиде.
- В частности, если — центроид треугольника то для любой точки верно, что
- .
- В частности, если — центроид треугольника то для любой точки верно, что
- Пусть — любая точка на плоскости, на которой лежит треугольник с вершинами , и ; и пусть — центроид этого треугольника, тогда сумма квадратов расстояний от до трёх вершин треугольника равна сумме квадратов расстояний от центроида до вершин треугольника плюс утроенный квадрат расстояния между и :
- [3].
- Сумма квадратов сторон треугольника равна утроенной сумме квадратов расстояний от центроида до вершин треугольника:
- [3].
- Центр масс сторон треугольника совпадает с центром вписанной окружности дополнительного треугольника (треугольника с вершинами, расположенными в серединах сторон данного треугольника). Эту точку называют центром Шпикера. Если стороны треугольника сделать из тонкой проволоки одинакового сечения, то центр масс (барицентр) полученной системы будет совпадать с инцентром дополнительного треугольника, или с центром Шпикера.
- О других свойствах центроида треугольника смотрите ниже.
Минимаксные свойства центроида треугольника[править | править код]
- Центроид или точка пресечения медиан треугольника является единственной точкой треугольника такой, что проведенные через неё три чевианы разделяют своими концами стороны треугольника на шесть отрезков. При этом произведение длин трёх из этих шести отрезков, не имеющих общих концов, максимально[4].
- Центроид или точка пересечения трёх медиан является точкой, для которой сумма квадратов расстояний до вершин треугольника принимает наименьшее значение (теорема Лейбница).
Центроид четырёх точек (вершин четырёхугольника)[править | править код]
Центроид (барицентр или центр масс) вершин произвольного четырёхугольника лежит в точке пересечения 3-х отрезков: 1-й отрезок соединяет середины диагоналей, два другие — середины противолежащих сторон. Точка пересечения делит все три отрезка пополам.
Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в одной точке (центроиде вершин четырёхугольника) и делятся ею в отношении 3:1, считая от вершины.
Центр масс вершин четырёхугольника не обязан совпадать с центром масс самого четырёхугольника как плоской фигуры.
Определение местоположения барицентра[править | править код]
Определение местоположения барицентра однородной плоской фигуры методом отвеса[править | править код]
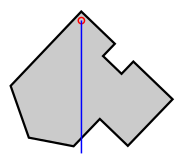
Барицентр однородной плоской фигуры, такой как фигура (a) на рисунке, можно найти экспериментально с использованием отвеса и булавки путём нахождения центра масс тонкой пластины однородной плотности, имеющей ту же форму. Пластина удерживается булавкой, вставленной ближе к периметру так, чтобы пластина могла свободно вращаться. Отмечаем на пластине прямую, которую образует отвес, прикреплённый к булавке (b). Проделываем то же самое с другим положением булавки. Пересечение двух прямых даст барицентр (c).

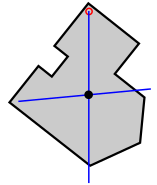
Этот метод можно распространить (в теории) на вогнутые фигуры, когда барицентр лежит вне их, а также тела (постоянной плотности), но положение линии отвеса придётся отмечать каким-то иным способом.
Определение местоположения барицентра выпуклой двумерной фигуры методом балансировки[править | править код]
Барицентр выпуклой двумерной фигуры можно найти путём балансировки на меньшей фигуре, например, на вершине узкого цилиндра. Барицентр будет находиться где-то внутри области контакта этих фигур. В принципе, последовательным уменьшением диаметра цилиндра можно получить местоположение барицентра с любой точностью. На практике потоки воздуха делают это невозможным, однако используя наложение областей балансировки и усреднение, можно получить нужную точность.
Определение местоположения барицентра для конечного множества точек[править | править код]
Барицентр конечного множества из точек в находится по формуле
- [5].
Полученная точка такая, что сумма квадратов расстояний между ней и точками множества является минимальной.
Определение местоположения барицентра с помощью геометрического разложения[править | править код]



Барицентр плоской фигуры можно вычислить, разделив её на конечное число более простых фигур , найдя положение барицентров и площадей каждой части, а затем вычислив
Дыры в фигуре , наложения частей, или части, выступающие за фигуру, можно рассматривать как фигуры с отрицательной площадью . А именно, знак площади нужно выбирать так, чтобы сумма знаков для всех частей, включающих точку , была равна 1, если принадлежит , и 0 в противном случае.
Например, фигуру (a) на рисунке легко разделить на квадрат и треугольник с положительным знаком, круглое отверстие с отрицательным (b).
Барицентр каждой части легко найти в любом списке барицентров простых фигур (c). Затем вычисляется барицентр фигуры, как средневзвешенное трёх точек. Горизонтальное положение барицентра, считая от левого края фигуры, равно
Вертикальное положение вычисляется аналогично.
Та же формула применима для любого трёхмерного объекта, только обозначают уже объёмы частей тела , а не площади. Формула верна также для пространства любой размерности при замене площади -мерными мерами частей.
Определение местоположения барицентра интегрированием[править | править код]
Барицентр подмножества X пространства можно вычислить с помощью интеграла
где интегрирование ведётся по всему пространству , а g является характеристической функцией подмножества, принимающей 1 внутри X и 0 вне его[6]. Заметим, что знаменатель равен мере множества X. Формула неприменима к множеству нулевой меры, а также к множествам, для которых интеграл расходится.
Другая формула для вычисления координат барицентра:
где Gk является k-й координатой G, а Sk(z) — мера пересечения X с гиперплоскостью, определяемой уравнением xk = z. Снова знаменатель — это мера множества X.
Для плоской фигуры координатами барицентра будут
где A — площадь фигуры X, Sy(x) — длина пересечения[неизвестный термин] X с вертикальной прямой с абциссой x, Sx(y) — аналогичная величина при обмене осей.
Определение местоположения барицентра для области, ограниченной графиками непрерывных функций[править | править код]
Координаты барицентра области, ограниченной графиками непрерывных функций и , таких что на интервале , , задаются выражениями
- [6].
где — площадь области (вычисляемая по формуле )[8][9].
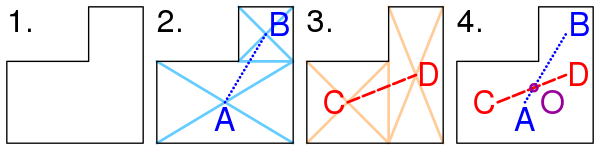
Определение местоположения барицентра объекта, имеющего форму буквы L[править | править код]
Метод нахождения барицентра фигуры, имеющей форму буквы L.
- Фигуру делят на два прямоугольника (см. фигуру (2) на рисунке). Находят барицентры A и B этих двух прямоугольников как пересечение диагоналей. Рисуют отрезок AB, соединяющий барицентры. Барицентр фигуры должен лежать на этом отрезке AB.
- Делят фигуру на два прямоугольника другим способом (см. фигуру (3) на рисунке). Находят барицентры C и D этих двух прямоугольников. Проводят отрезок CD, соединяющий барицентры. Барицентр фигуры должен лежать на отрезке CD.
- Поскольку барицентр должен лежать как на отрезке AB, так и на отрезке CD, очевидно, что он является точкой пересечения этих двух отрезков — точкой O. Точка O не обязана лежать внутри фигуры.
Барицентры треугольника и тетраэдра[править | править код]


Барицентр треугольника совпадает с пересечением медиан. Барицентр разбивает каждую медиану в отношении 2:1, то есть барицентр находится на расстоянии ⅓ от стороны до противоположной вершины (см. рисунок). Его декартовыми координатами является среднее координат трёх вершин. То есть, если вершинами треугольника являются , и , то координаты барицентра вычисляются по формуле
- .
Таким образом, барицентр имеет барицентрические координаты .
В трилинейных координатах барицентр можно получить одним из эквивалентных способов[10]:
Барицентр является также физически центром масс треугольника, сделанного из однородного листового материала, а также, если вся масса сконцентрирована в вершинах и одинаково разделена между ними. Если же масса распределена равномерно вдоль периметра, то центр масс лежит в точке Шпикера (инцентре серединного треугольника), который (в общем случае) не совпадает с центроидом всего треугольника.
Площадь треугольника равна 3/2 длины любой стороны, умноженной на расстояние от центроида до стороны[11].
Центроид треугольника лежит на прямой Эйлера между его ортоцентром и центром его описанной окружности , ровно вдвое ближе ко второму, чем к первому:
- .
Кроме того, для инцентра и центра девяти точек , мы имеем
- ,
- ,
- ,
- ,
- .
Аналогичными свойствами обладает тетраэдр — его барицентр является пересечением отрезков, соединяющих вершины с барицентрами противоположных граней. Эти отрезки делятся барицентром в отношении 3:1. Результат может быть обобщён на любой -мерный симплекс. Если вершины симплекса обозначить и рассматривать вершины как вектора, центроид равен
- .
Геометрический барицентр совпадает с центром масс, если масса равномерно распределена по всему симплексу или сосредоточена в вершинах как равных масс.
Изогональным сопряжением центроида треугольника является точка пересечения его симедиан.
Барицентр тетраэдра[править | править код]
Тетраэдр является телом в трёхмерном пространстве, имеющим четыре треугольника в качестве граней. Отрезок, соединяющий вершину тетраэдра с барицентром противоположной грани, называется медианой, а отрезок, соединяющий середины двух противоположных сторон, называется бимедианой. Таким образом, имеется четыре медианы и три бимедианы. Эти семь отрезков пересекаются в барицентре тетраэдра[12]. Барицентр тетраэдра лежит посередине между точкой Монжа и центром описанной сферы. Эти точки задают прямую Эйлера тетраэдра, являющуюся аналогом прямой Эйлера треугольника.
Барицентр многоугольника[править | править код]
Барицентром самонепересекающегося замкнутого многоугольника, заданного вершинами , , , , является точка , где
- ;
и где является площадью многоугольника (со знаком):
- [13].
В этой формуле предполагается, что вершины пронумерованы вдоль периметра многоугольника. Кроме того, вершина считается той же самой, что и . Заметим, что если точки пронумерованы по часовой стрелке, площадь , вычисленная выше, будет отрицательной, но координаты барицентра подкорректируют этот случай.
Барицентры конуса и пирамиды[править | править код]
Барицентр конуса или пирамиды расположен на отрезке, соединяющем вершину тела с барицентром основания. Для целого конуса или пирамиды барицентр находится на расстоянии 1/4 от основания к вершине. Для поверхности конуса или пирамиды (боковая поверхность без внутренности и без основания) центроид находится на 1/3 расстояния от основания до вершины.
См. также[править | править код]
- Центр масс
- Центроид треугольника
- Центр тяжести
- Центр Чебышева
- Среднее Фреше
- k-means
- Список барицентров
- Теоремы Паппа — Гульдина
- Замечательные точки треугольника
Примечания[править | править код]
- ↑ Altshiller-Court, 1925, с. 101.
- ↑ Kay, 1969, с. 18,189,225–226.
- ↑ 1 2 Altshiller-Court, 1925, с. 70–71.
- ↑ Зетель, 1962.
- ↑ Protter, Morrey, 1970, с. 520.
- ↑ 1 2 Protter, Morrey, 1970, с. 526.
- ↑ Protter, Morrey, 1970, с. 527.
- ↑ Protter, Morrey, 1970.
- ↑ Larson, Hostetler, Edwards, 1998, с. 458–460.
- ↑ Encyclopedia of Triangle Centers Архивная копия от 19 апреля 2012 на Wayback Machine by Clark Kimberling. The centroid is indexed as X(2).
- ↑ Johnson, 2007, с. 173.
- ↑ Kam-tim, Suk-nam, 1994, с. 53–54.
- ↑ Bourke, 1997.
Литература[править | править код]
- Балк, М. Б., Болтянский, В. Г. Геометрия масс. — М.: Наука, 1981. — (Библиотечка Кванта Вып. 61).
- Зетель, С. И. Новая геометрия треугольника. Пособие для учителей. — 2-е изд/. — М. : Учпедгиз, 1962. — С. 12.
- Leung Kam-tim, Suen Suk-nam. Vectors, matrices and geometry. — Hong Kong University Press, 1994.
- Nathan Altshiller-Court. College Geometry: An Introduction to the Modern Geometry of the Triangle and the Circle. — 2nd. — New York: Barnes & Noble, 1925.
- Paul Bourke. Calculating the area and centroid of a polygon. — 1997.
- Roger A. Johnson. Advanced Euclidean Geometry. — Dover, 2007.
- David C. Kay. College Geometry. — New York: Holt, Rinehart and Winston, 1969.
- Roland E. Larson, Robert P. Hostetler, Bruce H. Edwards. Calculus of a Single Variable. — 6th. — Houghton Mifflin Company, 1998.
- Murray H. Protter, Charles B. Morrey Jr. College Calculus with Analytic Geometry. — 2nd. — Reading: Addison-Wesley, 1970.
Ссылки[править | править код]
- Characteristic Property of Centroid at cut-the-knot
- Barycentric Coordinates at cut-the-knot
- Interactive animations showing Centroid of a triangle and Centroid construction with compass and straightedge
- Experimentally finding the medians and centroid of a triangle at Dynamic Geometry Sketches, an interactive dynamic geometry sketch using the gravity simulator of Cinderella.
Для улучшения этой статьи желательно:
|


































![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

![{\displaystyle {\bar {x}}={\frac {1}{A}}\int _{a}^{b}x\left[f(x)-g(x)\right]\;dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/179f55af42d95979aca89cc9489483ff4b9d2c5c)
![{\displaystyle {\bar {y}}={\frac {1}{A}}\int _{a}^{b}\left[{\frac {f(x)+g(x)}{2}}\right]\left[f(x)-g(x)\right]\;dx,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c87db980fc5df43dac74a068a0b669963c2c20a0)
![{\displaystyle \int _{a}^{b}\left[f(x)-g(x)\right]\;dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93510a18e05797cf028ead8acdb3ecede56d2440)