Квантовая электродинамика
Ква́нтовая электродина́мика (КЭД) — квантовополевая теория электромагнитных взаимодействий; наиболее разработанная часть квантовой теории поля. Классическая электродинамика учитывает только непрерывные свойства электромагнитного поля, в основе же квантовой электродинамики лежит представление о том, что электромагнитное поле обладает также и прерывными (дискретными) свойствами, носителями которых являются кванты поля — фотоны. Взаимодействие электромагнитного излучения с заряженными частицами рассматривается в квантовой электродинамике как поглощение и испускание частицами фотонов.
Квантовая электродинамика количественно объясняет эффекты взаимодействия излучения с веществом (испускание, поглощение и рассеяние), а также последовательно описывает электромагнитные взаимодействия между заряженными частицами. К числу важнейших проблем, которые не нашли объяснения в классической электродинамике, но успешно разрешаются квантовой электродинамикой, относятся тепловое излучение тел, рассеяние рентгеновских лучей на свободных (точнее, слабо связанных) электронах (эффект Комптона), излучение и поглощение фотонов атомами и более сложными системами, испускание фотонов при рассеянии быстрых электронов во внешних полях (тормозное излучение) и другие процессы взаимодействия электронов, позитронов и фотонов. Меньший успех теории при рассмотрении процессов с участием других частиц обусловлен тем, что в этих процессах, кроме электромагнитных взаимодействий, играют важную роль и другие фундаментальные взаимодействия (сильное и слабое).

С математической точки зрения КЭД можно описать как теорию возмущений электромагнитного вакуума. Ричард Фейнман назвал её «жемчужиной физики» за чрезвычайно точные предсказания таких величин, как аномальный магнитный момент электрона и лэмбовский сдвиг энергетических уровней атома водорода[1]:Ch1.
История[править | править код]

Первую формулировку квантовой теории, которая описывала взаимодействие излучения и материи, приписывают британскому физику Полу Дираку, который (в течение 1920-х годов) смог вычислить коэффициент спонтанного излучения атома.[2][3]
Дирак рассмотрел квантование электромагнитного поля как ансамбль гармонических осцилляторов с использованием концепции операторов рождения и уничтожения частиц.[4] В последующие годы, благодаря вкладам Вольфганга Паули, Юджина Вигнера, Паскуаля Йордана, Вернера Гейзенберга и элегантной формулировке квантовой электродинамики Энрико Ферми[5] физики пришли к выводу, что в принципе возможно провести любые вычисления для любого физического процесса с участием фотонов и заряженных частиц. Однако дальнейшие исследования Феликса Блоха с Арнольдом Нордсиком[6] и Виктором Вайскопфом[7] в 1937 и 1939 годах показали, что такие вычисления оказались надежными только в первом порядке теории возмущений — проблема, ранее отмеченная Робертом Оппенгеймером.[8] На более высоких порядках в серии возникали бесконечности, делающие такие вычисления бессмысленными и вызывающие серьёзные сомнения во внутренней непротиворечивости самой теории. Поскольку в то время не было известно решение этой проблемы, казалось, что существует фундаментальная несовместимость между специальной теорией относительности и квантовой механикой.

Трудности с теорией росли до конца 1940-х годов. Улучшения в микроволновой технике позволили провести более точные измерения сдвига уровней атома водорода[9], ныне известного как лэмбовский сдвиг, и магнитного момента электрона.[10] Эти эксперименты выявили несоответствия, которые теория не могла объяснить.
Первое указание на возможный выход из положения было дано Гансом Бете в 1947 году после посещения конференции острова Шелтер[11]. На поезде от конференции до Скенектади он сделал первое нерелятивистское вычисление сдвига линий атома водорода, измеренного Лэмбом и Ризерфордом.[12] Несмотря на ограничения вычислений, согласие было отличным. Идея заключалась в том, чтобы просто добавить бесконечности к поправкам на массу и заряд, которые фактически были зафиксированы на конечном значении экспериментально. Таким образом, бесконечности поглощаются этими константами и дают конечный результат, хорошо согласующийся с экспериментом. Эта процедура получила название перенормировки.

Основываясь на интуиции Бете и фундаментальных работах по этому вопросу Синъитиро Томонаги,[13] Джулиана Швингера,[14][15] Ричарда Фейнмана[16][17][18] и Фримена Дайсона,[19][20] наконец стало возможным получить полностью ковариантные формулировки, конечные в любом порядке в ряду теории возмущений для квантовой электродинамики. Синъитиро Томонага, Джулиан Швингер и Ричард Фейнман были совместно удостоены Нобелевской премии 1965 года по физике за свои работы в этой области.[21] Их вклад и вклад Фримена Дайсона касались ковариантных и калибровочно-инвариантных формулировок квантовой электродинамики, которые позволяют вычислять наблюдаемые в любом порядке теории возмущений. Математическая техника Фейнмана, основанная на его диаграммах, поначалу казалась очень отличающейся от теоретико-полевого подхода, основанного на операторах Швингера и Томонаги, но Фримен Дайсон показал, что эти два подхода эквивалентны. Перенормировка, то есть необходимость придать физический смысл некоторым бесконечностям, появляющимся в теории, через интегралы, впоследствии стала одним из фундаментальных аспектов квантовой теории поля и стала рассматриваться как критерий общей согласованности теории. Несмотря на то, что на практике перенормировка работает очень хорошо, Фейнман никогда не чувствовал себя полностью уверенным в её математической достоверности, даже говоря о перенормировке как о «игре в ракушки» и «фокусе-покусе»[1]:128.
КЭД послужила моделью и шаблоном для всех последующих квантовых теорий поля. Одной из таких последующих теорий — квантовая хромодинамика, которая зародилась в начале 1960-х и приобрела свою нынешнюю форму в 1970-х годах в работах Х. Дейвида Политцера, Сидни Коулмана, Дэвида Гросса и Фрэнка Вильчека. Основываясь на новаторских работах Швингера, Джеральда Гуральника, Дика Хагена, Тома Киббла,[22][23] Питера Хиггса, Джеффри Голдстоуна и других, Шелдон Ли Глэшоу, Стивен Вайнберг и Абдус Салам независимо друг от друга показали, как слабое взаимодействие и квантовая электродинамика могут быть объединены в одно общее электрослабое взаимодействие.
Взгляд Фейнмана на квантовую электродинамику[править | править код]
Вступление[править | править код]
Ближе к концу своей жизни Ричард Фейнман прочитал серию лекций по КЭД, предназначенных для широкой публики. Эти лекции были переписаны и опубликованы в виде книги Фейнмана в 1985 году, QED: The Strange Theory of Light and Matter[1] — классическое нематематическое изложение QED с точки зрения, которая выглядит следующим образом.
Ключевыми компонентами КЭД, предложенной Фейнманом, являются три основных процесса.[1]:85
- Фотон перемещается из одного положения в пространстве и времени в другое.
- Электрон перемещается из одного положения в пространстве и времени в другое.
- Электрон излучает или поглощает фотон в определённой точке пространства и в определённое время.

Эти процессы представлены в виде упрощённой визуализации с помощью трех основных элементов диаграмм Фейнмана: волнистой линии для фотона, прямой — для электрона и соединения двух прямых линий и волнистой линии для обозначения вершины, представляющей излучение или поглощение фотона электроном (см. рисунок).
Помимо визуального обозначения процессов, Фейнман вводит ещё один вид обозначения для числовых величин, называемых амплитудами вероятности. Вероятность — это квадрат абсолютного значения полной амплитуды вероятности: . Если фотон движется из одного положения в пространстве и времени в другое положение пространства и времени, то связанная величина записывается в сокращении Фейнмана как . Аналогичная величина для электрона, движущегося из к записывается как . Величину, которая говорит об амплитуде вероятности испускания или поглощения фотона, он называет j. Она связана с элементарным зарядом электрона e, но не тождественна ему.[1]:91
КЭД основана на предположении, что сложные взаимодействия многих электронов и фотонов можно представить путем подбора подходящего набора из трех вышеуказанных строительных блоков и последующего использования амплитуд вероятности для вычисления вероятности любого такого сложного взаимодействия. Оказывается, что основную идею КЭД можно выразить, если предположить, что квадрат суммы амплитуд вероятности, упомянутых выше (P (от A к B), E (от C к D) и j), действует так же, как наша повседневная вероятность (упрощение, сделанное в книге Фейнмана). Позже, вслед за Фейнманом, эта формулировка будет исправлена, чтобы включить в неё математику, относящуюся к квантовому стилю.
Основные правила амплитуд вероятности, которые будут использоваться, следующие:[1]:93
- Каждому событию квантовой электродинамики (например, перемещению фотона или электрона из одной точки пространства-времени в другую или испусканию или поглощению фотона электроном) соответствует комплексное число — амплитуда вероятности события. Вероятность события равна квадрату модуля амплитуды вероятности события.
- Если событие может произойти взаимоисключающими способами, амплитуды вероятностей событий складываются. Если событие происходит поэтапно или в результате ряда независимых событий, амплитуды вероятностей событий перемножаются.
Основные конструкции[править | править код]
Предположим, мы начинаем с одного электрона в определённой пространственной позиции и в определённое время (этому месту и времени присвоена произвольная метка А) и фотона в другой точке пространства и времени (с меткой В). Типичный вопрос с физической точки зрения: «Какова вероятность найти электрон в C (другая координата и более поздний момент времени) и фотон в D (еще одна координата и время)?» . Самый простой процесс для достижения этой цели — это перемещение электрона из точки A в точку C (элементарное действие) и перемещение фотона из точки B в точку D (еще одно элементарное действие). Зная амплитуды вероятности каждого из этих подпроцессов — E (от A в C) и P (от B в D) — можно вычислить амплитуду вероятности того, что оба процесса происходят одновременно, умножая их, используя правило b). Это дает простую оценку общей амплитуды вероятности, которая возводится в квадрат для получения вероятности.

Но есть и другие способы достижения конечного результата. Электрон может переместиться в точку и время E, где он поглотит фотон; затем двигается дальше, прежде чем испустить ещё один фотон в точке F; затем переходит к C, где он регистрируется, а новый фотон переходит к D. Вероятность этого сложного процесса можно снова рассчитать, зная амплитуды вероятности каждого из отдельных процессов: трех процессов для электрона, двух процессов для фотонов и двух вершин — одной для излучения и одной для поглощения. Для нахождения полной амплитуды вероятности, умножаются амплитуды вероятности каждого из процессов для любых выбранных координат E и F. Затем, используя правило а), нужно сложить все эти амплитуды вероятностей для всех возможностей для E и F. На практике эта процедура не элементарна и предполагает интегрирование. Но есть и другая возможность, заключающаяся в том, что электрон сначала движется в G, где он испускает фотон, который переходит в D, а электрон движется в H, где он поглощает первый фотон, прежде чем перейти к C. Опять же, можно вычислить амплитуду вероятности этих процессов (для всех точек G и H). Это улучшит оценку общей амплитуды вероятности, добавив амплитуды вероятностей этих двух возможностей к первоначальной простой оценке. Этот процесс взаимодействия фотона с электроном называется комптоновским рассеянием.
Существует бесконечное число других промежуточных процессов, в которых все больше и больше фотонов поглощается и/или испускается. Для каждой из этих возможностей существует диаграмма Фейнмана, описывающая её. Это подразумевает сложные вычисления результирующих амплитуд вероятности, но при условии, что чем сложнее диаграмма, тем меньше она влияет на результат. Нахождение настолько точного ответа, насколько это необходимо — это вопрос времени и усилий. Такой подход для КЭД — основной. Чтобы рассчитать вероятность любого процесса взаимодействия между электронами и фотонами, нужно сначала выбрать с помощью диаграмм Фейнмана все возможные способы, которыми этот процесс может быть построен используя три основных элемента. Каждая диаграмма включает в себя некоторые вычисления, учитывающие определённые правила, для нахождения соответствующих амплитуд вероятности.
Эта базовая процедура остается при переходе к квантовому описанию, но необходимы некоторые концептуальные изменения. Можно было бы ожидать в повседневной жизни, что будут накладываться какие-то ограничения на точки, в которой частица может находиться, но это не так в квантовой электродинамике. Существует возможность того, что электрон в точке A или фотон в точке B переместится в качестве основного процесса в любое другое место и время во Вселенной. Это включает в себя положения в пространстве, которые можно было достичь только со скоростью большей, чем скорость света, и даже в более ранние времена. Электрон, движущийся назад во времени, можно рассматривать как позитрон, движущийся вперед во времени.[1]:89, 98–99
Амплитуды вероятности[править | править код]

Квантовая механика вносит важное изменение в способ вычисления вероятностей. Вероятности по-прежнему представлены обычными действительными числами, которые мы используем для вероятностей в нашем повседневном мире, но они вычисляются как квадрат модуля амплитуды вероятностей, которые представляются комплексными числами.
Фейнман избегает знакомить читателя с математикой комплексных чисел, используя простое, но точное представление их в виде стрелок на листе бумаги или экране. Их не следует путать со стрелками в диаграммах Фейнмана, которые представляют собой упрощенные представления в двух измерениях отношений между точками в трёх измерениях пространства и одном измерении времени. Стрелки амплитуды имеют фундаментальное значение для описания мира в квантовой теории. Они связаны с нашими повседневными представлениями о вероятности простым правилом: вероятность события равна квадрату длины соответствующей амплитуды стрелки. Таким образом, для данного процесса, если задействованы две амплитуды с вероятностью, v и w, то вероятность процесса будет определяться формулой
Правила сложения и умножения такие же, но там, где складываются или умножаются вероятности, нужно вместо этого складывать или умножать амплитуды вероятностей, которые теперь представляют собой комплексные числа.

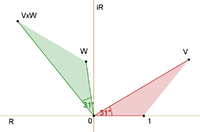
Сложение и умножение — обычные операции в теории комплексных чисел, они представлены на рисунках. Сумма находится следующим образом. Пусть начало второй стрелки будет в конце первой. Сумма представляет собой третью стрелку, идущую прямо от начала первой до конца второй. Произведение двух стрелок — это стрелка, длина которой равна произведению двух длин. Направление произведения определяется путем сложения углов, на которые были повёрнуты эти стрелки относительно опорного направления.
Это изменение от вероятностей к амплитудам вероятностей усложняет математику, но не изменяет основной подход. Этого изменения все ещё недостаточно, потому что при этом не учитывается тот факт, что и фотоны, и электроны могут быть поляризованными, то есть их ориентацию в пространстве и времени необходимо также принять во внимание. Следовательно, P (от A к B) состоит из 16 комплексных чисел или стрелок амплитуды вероятности.[1]:120–121 Есть также некоторые незначительные изменения, связанные с величиной j, которую, возможно, придется повернуть на кратное 90° для некоторых поляризаций, что представляет интерес только для детального рассмотрения.
С поляризацией электронов связана ещё одна небольшая особенность, а именно необходимость учитывать фермионую статистику или распределение Ферми — Дирака. Основное правило состоит в том, что если есть амплитуда вероятности для данного сложного процесса, включающего более одного электрона, то, когда учитывается дополнительная диаграмма Фейнмана, в которой рассматривается обмен двух электронных событий, то результирующая амплитуда меняет знак. В простейшем случае двае диаграммы электронов начинаются с A и B и заканчиваются в C и D. Амплитуда должна быть вычислена как «разница», E(A to D) × E(B to C) − E(A to C) × E(B to D), где ожидается, исходя из нашего повседневного представления о вероятностях, сумма.[1]:112–113
Пропагаторы[править | править код]
Наконец, необходимо вычислить P (от A к B) и E (от C к D), соответствующие амплитудам вероятности для фотона и электрона. По сути, это решения уравнения Дирака, которые описывают поведение амплитуды вероятности электрона, и уравнений Максвелла, описывающих поведение амплитуды вероятности фотона. Их называют пропагаторами Фейнмана. Перевод в обозначения, обычно используемые в стандартной литературе, выглядит следующим образом:
где сокращенный символ, такой как обозначает четыре действительных числа, которые показывают время и положение в трёх измерениях точки, обозначенной буквой A.
Перенормировка массы[править | править код]

Исторически возникла проблема, которая задержала прогресс на двадцать лет: хотя рассмотрение процесса начинается с предположения о трех основных «простых» процессах, но чтобы вычислить амплитуду вероятности перехода электрона из точки A в точку B, нужно принять во внимание все возможные способы, то есть все возможные диаграммы Фейнмана с этими конечными точками. Таким образом, электрон может переместиться в точку C, испустить там фотон, а затем снова поглотить его в точке D прежде, чем перейти к точке B. Или он может повторить такой процесс дважды и больше раз. Короче говоря, существует фрактальная ситуация, в которой, при внимательном рассмотрении линии, она распадается на набор «простых» линий, каждая из которых при внимательном рассмотрении, в свою очередь, состоит из «простых» линий и так далее до бесконечности. Это сложная ситуация. Если бы добавление этой детали лишь немного изменило ситуацию, это было бы неплохо, но случилась катастрофа, когда было обнаружено, что упомянутая выше простая поправка привела к бесконечным амплитудам вероятности. Со временем эта проблема была «исправлена» методом перенормировки. Однако сам Фейнман остался недоволен этим, назвав это «дурацким процессом».[1]:128
Выводы[править | править код]
В рамках вышеупомянутой структуры, физики смогли вычислить с высокой степенью точности некоторые свойства электронов, такие как аномальный магнитный дипольный момент. Однако, как указывает Фейнман, он не может объяснить, почему частицы, такие как электрон, обладают определённой массой. "Не существует теории, адекватно объясняющей эти цифры. Мы используем числа во всех наших теориях, но не понимаем их — что это такое и откуда они взялись. Я считаю, что с фундаментальной точки зрения это очень интересная и серьёзная проблема "[1]:152
Математическая формулировка[править | править код]
Математически КЭД — это абелева калибровочная теория поля с группой симметрии U(1). Калибровочное поле, которое переносит взаимодействие между заряженными полями спина 1/2, является электромагнитным полем[24]:78.
Лагранжиан КЭД для поля спина 1/2 (электрон-позитронного поля), взаимодействующего с электромагнитным полем, равен сумме лагранжианов электрон-позитронного поля, фотонного поля и слагаемого, описывающего взаимодействие электромагнитного поля с электрон-позитронным полем. Последнее слагаемое, однако, часто объединяют с первым, используя так называемую обобщённую ковариантную производную:
где
- — матрицы Дирака ;
- биспинорное поле частиц со спином 1/2 (например, электрон- позитронное поле);
- , называемый «пси-бар», иногда называют сопряженным по Дираку;
- — калибровочная ковариантная производная ;
- е — константа связи, равная электрическому заряду биспинорного поля;
- m — масса электрона или позитрона;
- — ковариантный четырехпотенциал электромагнитного поля, создаваемого самим электроном;
- — внешнее поле, создаваемое внешним источником;
- — тензор электромагнитного поля .
Уравнения движения[править | править код]
Подставляя определение D в лагранжиан, получаем
Из этого лагранжиана можно получить уравнения движения для полей ψ и A.
- Используя теоретико -полевое уравнение Эйлера — Лагранжа для ψ ,
Производные лагранжиана относительно ψ равны
Подставляя их в (2)
с эрмитово сопряженным уравнением
Перенос среднего члена в правую часть дает
Левая часть похожа на исходное уравнение Дирака, а правая часть описывает взаимодействие с электромагнитным полем.
- Используя уравнение Эйлера — Лагранжа для поля A,
на этот раз производные
Подстановка обратно в (3) приводит к
Теперь, если принять калибровочное условие Лоренца
уравнения сводятся к
которое является волновым уравнением для четырёхпотенциала, КХД-версии классических уравнений Максвелла в калибровке Лоренца . (Квадрат обозначает оператор Даламбера, .)
Представление взаимодействия[править | править код]
Эту теорию можно напрямую проквантовать, рассматривая бозонный и фермионный секторы для свободных частиц. Это позволяет построить набор асимптотических состояний, которые можно использовать для вычисления амплитуд вероятностей для различных процессов. Для этого нужно вычислить оператор эволюции, который для данного начального состояния приводит к конечному состоянию таким образом, чтобы выполнялось условие[24]:5
Этот метод также известен как метод S-матриц. Оператор эволюции получается в картине взаимодействия, где эволюция во времени задается гамильтонианом взаимодействия, который представляет собой интеграл по пространству от второго члена в плотности лагранжиана, приведенного выше:[24]:123
Или[24]:86
где T — оператор временного упорядочивания. Этот оператор эволюции имеет значение только в виде ряда. Получается ряд теории возмущений с постоянной тонкой структуры в качестве малого параметра. Этот ряд называется рядом Дайсона.
Метод возмущений[править | править код]
Основным вычислительным методом квантовой электродинамики является метод возмущений. В нулевом приближении электромагнитным взаимодействием пренебрегают, и частицы считаются невзаимодействующими. В первом, втором и т. д. приближениях учитываются однократные, двукратные и т. д. акты взаимодействия между частицами. Вероятность каждого акта взаимодействия пропорциональна заряду частицы . Чем больше актов взаимодействия рассматривается, тем в более высокой степени входит заряд в выражение для амплитуды вероятности процесса[25]. Вычисления в квантовой электродинамике заключаются в нахождении из лагранжиана, описывающего взаимодействие элементарных частиц, эффективных сечений реакций и скоростей распада частиц. Для вычислений по методу возмущений используется метод диаграмм Фейнмана, при помощи которых вычисляются матричные элементы, входящие в выражения для вероятностей переходов[26].
Диаграммы Фейнмана[править | править код]
Несмотря на концептуальную ясность подхода Фейнмана к КЭД, почти ни в одном из ранних учебников его изложение не давалось последовательно. При проведении вычислений гораздо проще работать с преобразованиями Фурье пропагаторов. Экспериментальные проверки квантовой электродинамики обычно представляют собой эксперименты по рассеянию. В теории рассеяния учитываются импульсы частиц, а не их положения, и удобно думать о частицах как о создаваемых или аннигилирующих при взаимодействии. Тогда диаграммы Фейнмана выглядят одинаково, но линии имеют разную интерпретацию. Электронная линия представляет собой электрон с заданной энергией и импульсом и аналогично для фотонной линии. Вершинная диаграмма представляет собой аннигиляцию одного электрона и создание другого вместе с поглощением или созданием фотона, каждый из которых имеет определённые энергии и импульсы.
Используя теорему Вика о членах ряда Дайсона, все члены S-матрицы для квантовой электродинамики можно вычислить с помощью техники диаграмм Фейнмана. В этом случае правила изображения следующие[24]:801–802


К этим правилам нужно добавить ещё одно для замкнутых контуров, которое подразумевает интегрирование по импульсам , поскольку эти внутренние («виртуальные») частицы не ограничены какой-либо определённой энергией-импульсом, даже той, которая обычно требуется специальной теорией относительности (см. детали в Propagator).
На их основе непосредственно вычисляются амплитуды вероятностей. Примером может служить комптоновское рассеяние, когда электрон и фотон подвергаются упругому рассеянию. В данном случае диаграммы Фейнмана[24]:158–159

и поэтому соответствующая амплитуда в первом порядке ряда возмущений для S-матрицы примет вид
из которого вычисляют сечение этого рассеяния.
Непертурбативные явления[править | править код]
Успех предсказаний квантовой электродинамики во многом основан на использовании теории возмущений, выраженной в диаграммах Фейнмана. Однако квантовая электродинамика также приводит к предсказаниям, выходящим за рамки теории возмущений. В присутствии очень сильных электрических полей она предсказывает, что электроны и позитроны будут спонтанно образовываться, вызывая распад поля. Этот процесс, называемый эффектом Швингера[27], который нельзя понять в терминах какого-либо конечного числа диаграмм Фейнмана и, следовательно, описывается как непертурбативный. Математически это может быть получено с помощью полуклассического приближения в терминах интегралов по траекториям в квантовой электродинамике.
Перенормируемость[править | править код]
Члены более высокого порядка вычисляются напрямую для оператора эволюции, но эти члены отображаются диаграммами, содержащими следующие более простые петли[24]:ch 10
-
Однопетлевой вклад в функцию поляризации вакуума
-
Однопетлевой вклад в функцию собственной энергии электрона
-
Однопетлевой вклад в вершинную функцию
которые, будучи замкнутыми контурами, подразумевают наличие расходящихся интегралов, не имеющих математического значения. Чтобы преодолеть эту трудность, была разработана техника, называемая перенормировкой, дающая конечные результаты, очень хорошо согласующиеся с экспериментами. Критерием осмысленности теории после перенормировки является конечное число расходящихся диаграмм. В этом случае теория называется «перенормируемой». Причина этого состоит в том, что для перенормировки наблюдаемых требуется конечное число констант, чтобы не нарушить предсказательную ценность теории. Это как раз тот случай, когда квантовая электродинамика отображает всего три расходящиеся диаграммы. Эта процедура дает наблюдаемые в очень хорошем соответствии с экспериментом, как видно, например, для гиромагнитного отношения электронов.
Перенормируемость стала важным критерием для того, чтобы квантовая теория поля считалась жизнеспособной. Все теории, описывающие фундаментальные взаимодействия, за исключением гравитации, квантовый аналог которой только предполагается и в настоящее время очень активно исследуется, являются перенормируемыми теориями.
Расходящиеся ряды[править | править код]
Аргумент Фримена Дайсона показывает, что радиус сходимости ряда теории возмущений в КЭД равен нулю.[28] Основной аргумент заключается в следующем: если бы константа связи была отрицательной, это было бы эквивалентно отрицательной силе Кулона. Такое «обратное» электромагнитное взаимодействие соответствует тому, что одноимённые заряды будут притягиваться и разноимённые — отталкиваться. Это сделало бы вакуум нестабильным по отношению к распаду на скопление электронов на одной стороне вселенной и скопление позитронов на другой стороне вселенной. Поскольку теория «больна» при любом отрицательном значении константы связи, ряды расходятся, и в лучшем случае имеют свойства асимптотических рядов.
С современной точки зрения говорится, что КЭД не может быть определена как квантовая теория поля для произвольно высоких энергий.[29] Константа связи стремится к бесконечности при конечной энергии, сигнализируя о полюсе Ландау. Проблема состоит в том, что КХД, похоже, страдает проблемами квантовой тривиальности. Это одна из причин включения КХД в Теорию Великого Объединения.
Опыты по проверке квантовой электродинамики[править | править код]
Дифференциальное и полное сечения рассеяния эффекта Комптона, процесса рассеяния электрона на электроне и позитроне, процессов взаимодействия фотонов с атомами и ядрами, аномальный магнитный момент и лэмбовский сдвиг электрона с высокой точностью совпадают с расчетами квантовой электродинамики[30][31][32].
Нерешённые проблемы квантовой электродинамики[править | править код]
Энергия вакуума[править | править код]
Вакуумом в квантовой электродинамике называется состояние, в котором у всех осцилляторов . Следовательно, энергия каждого осциллятора равна , где — собственная частота осциллятора. Сумма всех мод осцилляторов с частотами от нуля до бесконечности равна бесконечности. На практике этой расходимостью пренебрегают и энергию вакуумного состояния принимают равной нулю. Остаётся открытым вопрос: не образуется ли вакуум гравитационного поля, подобно массе, распределенной с постоянной плотностью? По «правилу обрезания», моды с очень большими частотами исключаются из рассмотрения. Плотность энергии вакуумного состояния
- .
Подставляя значение , где — масса протона, получаем значение плотности массы, эквивалентное этой энергии: грамм на кубический сантиметр пространства. Гравитационные эффекты, соответствующие этой энергии вакуума, не обнаружены[33]. Не удается вычислить энергию вакуума как собственное значение для гамильтониана вакуумного состояния, а при применении методов теории возмущений к расчету вероятности перехода из вакуумного состояния в состояние с фотоном и электронно-позитронной парой получаются расходящиеся интегралы[34].
Расходимость рядов[править | править код]
При расчёте вероятностей процессов в квантовой электродинамике методом возмущений к выражению для амплитуды процесса последовательно добавляются слагаемые вида , где — постоянная тонкой структуры, — число вершин на диаграммах Фейнмана в данном приближении. Ряды вида являются расходящимися. В опытах данная расходимость не проявляется, поскольку предельная точность вычислений при помощи таких рядов составляет %[25].
Расходимость интегралов[править | править код]
Требование локальности взаимодействия между частицами в квантовой электродинамике приводит к тому, что интегралы по пространству, описывающие процессы взаимодействия частиц, оказываются расходящимися за счёт больших импульсов виртуальных частиц. Это свидетельствует о неприменимости принятых в квантовой электродинамике методов описания взаимодействий на малых расстояниях[35].
Примечания[править | править код]
- ↑ 1 2 3 4 5 6 7 8 9 10 11 Фейнман Р. КЭД — странная теория света и вещества. — Серия Библиотечка «Квант». — М.: Наука, 1988. — 144 с. Архивировано 24 мая 2007 года.
- ↑ P. A. M. Dirac (1927). "The Quantum Theory of the Emission and Absorption of Radiation". Proceedings of the Royal Society of London A. 114 (767): 243—65. Bibcode:1927RSPSA.114..243D. doi:10.1098/rspa.1927.0039.
- ↑ П.А.М. Дирак Квантовая теория испускания и поглощения излучения // Эйнштейновский сборник, 1984-1985. - М., Наука, 1988. - с. 215-245
- ↑ А. Б. Кожевников Дирак и квантовая теория излучения // Эйнштейновский сборник, 1984-1985. - М., Наука, 1988. - с. 246-270
- ↑ E. Fermi (1932). "Quantum Theory of Radiation". Reviews of Modern Physics. 4 (1): 87—132. Bibcode:1932RvMP....4...87F. doi:10.1103/RevModPhys.4.87.
- ↑ Bloch, F. (1937). "Note on the Radiation Field of the Electron". Physical Review. 52 (2): 54—59. Bibcode:1937PhRv...52...54B. doi:10.1103/PhysRev.52.54.
- ↑ V. F. Weisskopf (1939). "On the Self-Energy and the Electromagnetic Field of the Electron". Physical Review. 56 (1): 72—85. Bibcode:1939PhRv...56...72W. doi:10.1103/PhysRev.56.72.
- ↑ R. Oppenheimer (1930). "Note on the Theory of the Interaction of Field and Matter". Physical Review. 35 (5): 461—77. Bibcode:1930PhRv...35..461O. doi:10.1103/PhysRev.35.461.
- ↑ Lamb, Willis (1947). "Fine Structure of the Hydrogen Atom by a Microwave Method". Physical Review. 72 (3): 241—43. Bibcode:1947PhRv...72..241L. doi:10.1103/PhysRev.72.241.
- ↑ Foley, H.M. (1948). "On the Intrinsic Moment of the Electron". Physical Review. 73 (3). Bibcode:1948PhRv...73..412F. doi:10.1103/PhysRev.73.412.
- ↑ Schweber, Silvan. Chapter 5 // QED and the Men Who Did it: Dyson, Feynman, Schwinger, and Tomonaga. — Princeton University Press, 1994. — P. 230. — ISBN 978-0-691-03327-3.
- ↑ H. Bethe (1947). "The Electromagnetic Shift of Energy Levels". Physical Review. 72 (4): 339—41. Bibcode:1947PhRv...72..339B. doi:10.1103/PhysRev.72.339.
- ↑ S. Tomonaga (1946). "On a Relativistically Invariant Formulation of the Quantum Theory of Wave Fields". Progress of Theoretical Physics. 1 (2): 27—42. Bibcode:1946PThPh...1...27T. doi:10.1143/PTP.1.27.
- ↑ J. Schwinger (1948). "On Quantum-Electrodynamics and the Magnetic Moment of the Electron". Physical Review. 73 (4): 416—17. Bibcode:1948PhRv...73..416S. doi:10.1103/PhysRev.73.416.
- ↑ J. Schwinger (1948). "Quantum Electrodynamics. I. A Covariant Formulation". Physical Review. 74 (10): 1439—61. Bibcode:1948PhRv...74.1439S. doi:10.1103/PhysRev.74.1439.
- ↑ R. P. Feynman (1949). "Space–Time Approach to Quantum Electrodynamics". Physical Review. 76 (6): 769—89. Bibcode:1949PhRv...76..769F. doi:10.1103/PhysRev.76.769.
- ↑ R. P. Feynman (1949). "The Theory of Positrons". Physical Review. 76 (6): 749—59. Bibcode:1949PhRv...76..749F. doi:10.1103/PhysRev.76.749.
- ↑ R. P. Feynman (1950). "Mathematical Formulation of the Quantum Theory of Electromagnetic Interaction" (PDF). Physical Review. 80 (3): 440—57. Bibcode:1950PhRv...80..440F. doi:10.1103/PhysRev.80.440. Архивировано (PDF) 19 апреля 2021. Дата обращения: 28 марта 2021.
- ↑ F. Dyson (1949). "The Radiation Theories of Tomonaga, Schwinger, and Feynman". Physical Review. 75 (3): 486—502. Bibcode:1949PhRv...75..486D. doi:10.1103/PhysRev.75.486.
- ↑ F. Dyson (1949). "The S Matrix in Quantum Electrodynamics". Physical Review. 75 (11): 1736—55. Bibcode:1949PhRv...75.1736D. doi:10.1103/PhysRev.75.1736.
- ↑ The Nobel Prize in Physics 1965. Nobel Foundation. Дата обращения: 9 октября 2008. Архивировано 21 октября 2008 года.
- ↑ Guralnik, G. S. (1964). "Global Conservation Laws and Massless Particles". Physical Review Letters. 13 (20): 585—87. Bibcode:1964PhRvL..13..585G. doi:10.1103/PhysRevLett.13.585.
- ↑ Guralnik, G. S. (2009). "The History of the Guralnik, Hagen and Kibble development of the Theory of Spontaneous Symmetry Breaking and Gauge Particles". International Journal of Modern Physics A. 24 (14): 2601—27. arXiv:0907.3466. Bibcode:2009IJMPA..24.2601G. doi:10.1142/S0217751X09045431.
- ↑ 1 2 3 4 5 6 7 Peskin, Michael. An introduction to quantum field theory / Michael Peskin, Daniel Schroeder. — Reprint. — Westview Press, 1995. — ISBN 978-0201503975.
- ↑ 1 2 Физика микромира, под ред. Д. В. Ширкова, М.:Наука.— 1980.— 528 с., тир. 50000 экз.
- ↑ Кейн, 1990, с. 15.
- ↑ Schwinger, Julian (1951-06-01). "On Gauge Invariance and Vacuum Polarization". Physical Review. 82 (5). American Physical Society (APS): 664—679. Bibcode:1951PhRv...82..664S. doi:10.1103/physrev.82.664. ISSN 0031-899X.
- ↑ Kinoshita, Toichiro Quantum Electrodynamics has Zero Radius of Convergence Summarized from Toichiro Kinoshita (англ.) (5 июня 1997). Дата обращения: 6 мая 2017. Архивировано 28 апреля 2021 года.
- ↑ Espriu and Tarrach (Apr 30, 1996). "Ambiguities in QED: Renormalons versus Triviality". Physics Letters B (англ.). 383 (4): 482—486. arXiv:hep-ph/9604431. Bibcode:1996PhLB..383..482E. doi:10.1016/0370-2693(96)00779-4.
- ↑ Широков Ю. М., Юдин Н. П. Ядерная физика.— М.: Наука.— 1972.
- ↑ Смондырев М. А. Квантовая электродинамика на малых расстояниях// Природа.— 1980.— № 9.
- ↑ Электромагнитные взаимодействия и структура элементарных частиц / ред. А. М. Балдин. — М: Мир.— 1969.— 327 с.
- ↑ Фейнман Р., Хибс А. Квантовая механика и интегралы по траекториям.— М.: Мир.— 1968.
- ↑ Дирак П. А. М. Принципы квантовой механики.— М.: Наука.— 1979.
- ↑ Мигдал А. Б. Качественные методы в квантовой теории.— М.: Наука.— 1975.
Литература[править | править код]
- De Broglie, Louis. Recherches sur la theorie des quanta [Research on quantum theory]. — France : Wiley-Interscience, 1925.
- Feynman, Richard Phillips. Quantum Electrodynamics. — Westview Press, 1998. — ISBN 978-0-201-36075-2.
- Jauch, J.M. The Theory of Photons and Electrons. — Springer-Verlag, 1980. — ISBN 978-0-387-07295-1.
- Greiner, Walter. Gauge Theory of Weak Interactions. — Springer, 2000. — ISBN 978-3-540-67672-0.
- Kane, Gordon, L. Modern Elementary Particle Physics. — Westview Press, 1993. — ISBN 978-0-201-62460-1.
- Miller, Arthur I. Early Quantum Electrodynamics: A Sourcebook. — Cambridge University Press, 1995. — ISBN 978-0-521-56891-3.
- Milonni, Peter W. The Quantum Vacuum: An Introduction to Quantum Electrodynamics. — Boston : Academic Press. — ISBN 0124980805.
- Schwinger, Julian. Selected Papers on Quantum Electrodynamics. — Dover Publications, 1958. — ISBN 978-0-486-60444-2.
- Tannoudji-Cohen, Claude. Photons and Atoms: Introduction to Quantum Electrodynamics. — Wiley-Interscience, 1997. — ISBN 978-0-471-18433-1.
- Физическая энциклопедия (гл. редактор А. М. Прохоров) — Квантовая электродинамика Архивная копия от 13 июня 2013 на Wayback Machine
- Грибов В. Н. Квантовая электродинамика.— Ижевск: РХД, 2001. — 288 с.
- Берестецкий В. Б., Лифшиц Е. М., Питаевский Л. П. Квантовая электродинамика. — Издание 4-е, исправленное. — М.: Физматлит.— 2002.— 720 с
- Видео Лекции: Квантовая электродинамика (профессор Фадин В. С., 2013 г.) Архивная копия от 18 февраля 2015 на Wayback Machine
- Кейн Г. Современная физика элементарных частиц. — М.: Мир, 1990. — 360 с. — ISBN 5-03-001591-4.
- Вальтер Е. Тирринг. Принципы квантовой электродинамики. — М.: Высшая школа, 1964. — 225 с.




































![{\displaystyle U=T\exp \left[-{\frac {i}{\hbar }}\int _{t_{0}}^{t}dt'\,V(t')\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39929208db730144caaaaf58ec4275d40b1a2db3)



















