Спонтанное нарушение симметрии

Рисунок «Потенциал с двумя ямами». Иллюстрация механизма спонтанного нарушения симметрии. Система может самостоятельно перейти в любую из двух потенциальных ям.

Спонта́нное наруше́ние симме́три́и — способ нарушения симметрии физической системы, при котором исходное состояние и уравнения движения системы инвариантны относительно некоторых преобразований симметрии, но в процессе эволюции система переходит в состояние, для которого инвариантность относительно некоторых (всех) преобразований начальной симметрии нарушается. Спонтанное нарушение симметрии всегда связано с вырождением состояния с минимальной энергией, называемым вакуумом. Множество всех вакуумов имеет начальную симметрию, однако каждый вакуум отдельно — нет. Например, шарик в желобе с двумя ямами скатывается из неустойчивого симметричного состояния в устойчивое состояние с минимальной энергией либо влево либо вправо, разрушая при этом симметрию относительно изменения левого на правое (операция инверсии).

Спонтанное нарушение симметрии происходит (псевдо) случайным образом и обусловлено флуктуациями. Это явление чрезвычайно распространенное в природе. Множество разнообразных примеров спонтанного нарушения симметрии можно привести в классической механике. Однако, тогда как в механике спонтанное нарушение симметрии имеет скорее описательное значение, в теории поля это основной принцип, обеспечивающий генерацию масс калибровочных бозонов. Более того, строя эффективные лагранжианы в квантовой теории поля, можно некоторые мезоны отождествить с соответствующими голдстоуновскими (псевдоголдстоуновскими) бозонами. Ниже рассмотрен пример π-мезона как голдстоуновского бозона при нарушении некоторой симметрии квантовой хромодинамики с безмассовыми кварками. Так же вещество в определённой термодинамической фазе можно рассматривать как квантовое поле с соответствующей симметрией. Тогда спонтанное нарушение симметрии представляется как фазовый переход.

Существование в природе четырёх фундаментальных взаимодействий тоже является следствием нарушения симметрии. Гипотетически при достаточно больших энергиях (~100 ГэВ) электромагнитные и слабые ядерные силы объединяются в одно электрослабое взаимодействие, а при ещё больших энергиях (~10 ¹⁴ ГэВ) объединяются электрослабое и сильное ядерное взаимодействия во взаимодействие Великого объединения.

Механизм спонтанного нарушения симметрии жизненно необходим для возможности существования суперсимметрии. Нарушенная суперсимметрия предполагает существование у каждой известной частицы суперпартнеров с такой же массой, чего не наблюдается в экспериментах. Считается, что из-за нарушения суперсимметрии суперпартнёры частиц приобретают большие массы, недосягаемые для современных ускорителей.

Вакуумы могут иметь довольно интересную структуру. Квантовая теория поля позволяет существование полевых вакуумных конфигураций со спонтанно нарушенными вакуумами, которые меняются от точки к точке. Такими состояниями являются например магнитные монополи, космические струны, доменные стенки. Состояния такого типа наблюдаются в физике конденсированного состояния, например, стенки между ферромагнитными доменами. При сложных конфигурациях потенциала с многими минимумами существует несколько вакуумов. Однако настоящим вакуумом является только состояние с наименьшей энергией. Все остальные вакуумы являются метастабильными и переходят в настоящий путем квантового туннелирования.

Спонтанное нарушение симметрии может играть большую роль и в гравитации. Считается, что космологическая инфляция вызвана переходом с фальшивого вакуума в истинный при спонтанном нарушении симметрии Великого объединения. Кроме того спонтанное нарушение суперсимметрии (суперхиггсовский механизм) предполагается в теориях массивной гравитации. Также развиваются модели гравитационного поля метрического тензора как Хиггс — Голдстоуновского поля некоторой нарушенной симметрии.

Таким образом спонтанное нарушение симметрии является чрезвычайно распространенным явлением во всех областях физики, начиная от классической механики, заканчивая квантовой гравитацией.

Простые примеры спонтанного нарушения симметрии

В классической механике

Уравнения, описывающие движение атомов любого несимметричного физического тела, например, кресла, инвариантны относительно трёхмерных поворотов, однако решение этих уравнений — реальное кресло — имеет определённую ориентацию в пространстве.

Шарик, находящийся посередине между ямами двухъямного желоба, рано или поздно под воздействием возмущений скатится в один из них, нарушая симметрию относительно замены $x\rightarrow -x.$

Карандаш, поставленный на торец на столе, не имеет никакого выделенного направления в плоскости стола, однако под действием возмущений упадет, выбрав о этом какое-то псевдо-случайное (зависимое от флуктуаций) направление.

Круглый металлический стержень, зажатый между пластинами пресса, при достаточной нагрузке согнётся, причём направление сгиба произвольно и зависит от флуктуаций. Начальная осевая симметрия стержня спонтанно нарушается.

Длина резинки увеличивается, а толщина уменьшается при растяжении. При определённом значении растягивающей силы она рвётся в определённом месте, хотя для идеальной резинки все места разрыва равновероятны. Причиной «нарушение» симметрии являются флуктуации толщины резинки — рвётся там где она тоньше. Идеальная резинка растянулась бы в цепочку из N атомов и порвалась бы, когда энергия растягивающей силы стала бы равной суммарной энергии связи атомов $E=N\varepsilon$.

В физике конденсированного состояния

При кристаллизации жидкости, характеризующейся высокой изотропией (симметрией), образуется кристалл, в котором существуют определённые выделенные направления относительно кристаллографических осей. Ориентация кристаллографических осей в общем случае случайна или обусловлена слабыми внешними факторами или флуктуациями. Также симметрия относительно трансляций на произвольный вектор снижается до трансляционной симметрии на вектор, который является линейной комбинацией векторов кристаллической решетки.

Жидкость при охлаждении ниже температуры кристаллизации превращается в кристалл. Однако жидкость без примесей может быть охлаждена ниже температуры кристаллизации. Такое положение достигается благодаря отсутствию центров кристаллизации — нет зародышей, на которых могли бы образовываться кристаллы, и образуется метастабильная фаза переохлажденной жидкости. С точки зрения симметрии, изотропная и трансляционная симметрия жидкости должна снизиться до симметрии кристаллической решетки, но отсутствуют флуктуации (центры кристаллизации), которые нарушают данную симметрию.

Аналогичная ситуация возникает в пересыщенном паре или перегретой жидкости. Такие метастабильные состояния используются например в пузырьковых камерах и камерах Вильсона.

Нагретые выше температуры Кюри ферромагнетики находятся в парамагнитном состоянии, где выделенного направления намагниченности нет, однако охлаждаясь ниже температуры Кюри в ферромагнетике возникает спонтанная намагниченность (происходит фазовый переход), направление которой (при отсутствии внешнего магнитного поля) является случайным и зависит от флуктуаций. Спонтанное нарушение симметрии происходит почти при всех фазовых переходах (см. Ниже).

В квантовой механике

Эксперимент с двумя щелями

При падении квантовой частицы на две щели в экране, за каждой из которых размещен детектор срабатывает (истинно случайным образом) один из детекторов. Симметрия случайно нарушается. Этот пример существенно отличается от упомянутых выше примеров тем, что, исходя из современных представлений (см. Теорема Белла), наличие флуктуаций для спонтанного нарушения симметрии не является обязательным условием, и природа реализует прохождение частицы через одну из возможных щелей совершенно случайным образом.

Измерения в квантовой механике

Допустимо прямое обобщение предыдущего примера на произвольное измерение состояния в квантовой механике. В квантовой теории, согласно постулату об измерениях, измерение заключается в редукции (мгновенном переходе) квантового состояния $|\psi \rangle$ в один из возможных собственных состояний $|a_{n}\rangle$ оператора ${\widehat {A}}$ измеряемой физической величины ${A}$. Состояние при этом случайным образом (с вероятностью $|\langle \psi |a_{n}\rangle |^{2}$) Переходит в состояние с нарушенной начальной симметрией.

Декогеренция

Основная статья: Квантовая декогеренция

Другим примером спонтанного нарушения симметрии в квантовой механике, но уже связанным с наличием флуктуаций, является декогеренция. Из-за наличия внешних флуктуаций чистое состояние системы переходит в смешанное с нарушением начальных симметрий. Математически это соответствует тому, что декогеренция вызывает зануления недиагональных элементов матрицы плотности.

Например, рассмотрим атом в возбужденном состоянии. Атом спонтанно излучает фотон и переходит на более низкий энергетический уровень. Если атом находится в сферически симметричном s-состоянии, то он излучает фотон в произвольном направлении, и сам перейдет в неизотропное l-состояние со спонтанно нарушенной симметрией относительно поворотов. Причиной нарушения симметрии является наличие окружающих частиц, а также случайные флуктуации физического вакуума.

Для иллюстрации декогеренции можно рассмотреть ансамбль одинаковых квантовых состояний. Из-за наличия внешних флуктуаций после определённого времени системы будут находиться в разных состояниях.

Именно уничтожение недиагональных элементов отвечает за спонтанное нарушение симметрии в первом примере данного раздела для кресла.

Спонтанное нарушение калибровочной симметрии

Рисунок «Линейная сигма-модель». Пример неинвариантного вакуума — линейная сигма-модель с группой симметрии SO(2).

Нарушение глобальной калибровочной симметрии

В теории поля обычно рассматривают динамику поля в окрестности вакуумного состояния (минимума потенциальной энергии), считая сами поля малыми. На практике, это ведёт к разложению функции Лагранжа соответствующего поля в ряд Тейлора в окрестности минимума потенциальной энергии и пренебрежение слагаемыми высших степеней. При этом выбор вакуума может быть неоднозначным (см. Рисунок «Линейная сигма модель»: серым цветом показаны возможные вакуумные состояния).

Например, рассмотрим лагранжиан комплексного (заряженного) поля Клейна — Гордона $\varphi =\varphi ^{1}+i\varphi ^{2},$ где $\varphi ^{1},\;\varphi ^{2}$ являются действительными полями,

${\mathcal {L}}={\frac {1}{2}}\partial ^{\mu }\varphi ^{*}\partial _{\mu }\varphi -V(\varphi ^{*}\varphi )={\frac {1}{2}}\partial ^{\mu }\varphi ^{1}\partial _{\mu }\varphi ^{1}+{\frac {1}{2}}\partial ^{\mu }\varphi ^{2}\partial _{\mu }\varphi ^{2}-V\left((\varphi ^{1})^{2}+(\varphi ^{2})^{2}\right)$,

где $V$ — потенциал взаимодействия, греческие индексы везде пробегают значения от 0 до 3. Этот лагранжиан инвариантен относительно глобальных калибровочных преобразований

$\varphi \rightarrow e^{i\alpha }\varphi ,\quad \left|\left|{\begin{array}{c}\varphi ^{1}\\\varphi ^{2}\end{array}}\right|\right|\rightarrow \left|\left|{\begin{array}{cc}\cos \alpha &\sin \alpha \\-\sin \alpha &\cos \alpha \end{array}}\right|\right|\left|\left|{\begin{array}{c}\varphi ^{1}\\\varphi ^{2}\end{array}}\right|\right|$,

где $\alpha$ — действительная константой. Для данной модели вакуум не инвариантен относительно таких калибровочных преобразований, если функция $V(x)$ имеет минимум в точке отличной от нуля. Покажем, что если $V(x)$ имеет минимум в нуле, то точке вакуума однозначно соответствует пара $\varphi ^{1}=0,\;\varphi ^{2}=0$. Совсем другая ситуация возникает в случае, когда $x_{min}=a^{2}\neq 0$. Минимуму потенциала соответствует не одна точка, а континуум точек

$(\varphi ^{1})^{2}+(\varphi ^{2})^{2}=a^{2}$.

Соответствующим поворотом системы координат пространства зарядовых степеней свободы поля Клейна — Гордона всегда можно привести вакуум к виду

$\varphi _{0}=\left|\left|0,a\right|\right|^{T}$.

Легко видеть, что хотя лагранжиан (в частности, приближенный) инвариантен относительно калибровочных преобразований, вакуум — нет. Система переходит в случайно выбранное (на самом деле в зависимости от флуктуаций) состояние. В этом и заключается спонтанное нарушение глобальной калибровочной симметрии.

Пример 1. Нарушение симметрии относительно инверсии знака действительного поля Клейна — Гордона

Рассмотрим простой пример спонтанного нарушения симметрии для действительного поля Клейна — Гордона, которое задаётся лагранжианом

${\mathcal {L}}=\partial ^{\mu }\varphi \partial _{\mu }\varphi -\left(\mu ^{2}\varphi ^{2}+{\frac {1}{2}}\lambda \varphi ^{4}\right)$,

где $\lambda >0$, $\mu ^{2}<0$. Видно, что лагранжиан инвариантен относительно замены $\varphi \rightarrow -\varphi$. Поле в этом случае имеет два вакуума, что соответствует наличию двух минимумов в потенциальной энергии при $\varphi _{0}=a=\pm {\sqrt {-\mu ^{2}/\lambda }}$. Оба вакуума не является инвариантным относительно начальной симметрии инверсии знака поля. В этом и заключается спонтанное нарушение симметрии. Здесь инверсия не является калибровочным преобразованием. Благодаря симметрии лагранжиана относительно инверсии знака поля (чётности), можно выбрать любой знак вакуума. Не умаляя общности можно выбрать «+». Разложив поле в окрестности вакуумного состояния $\varphi =a+\phi (x)$ и, считая $\phi (x)$ малой величиной, лагранжиан можно записать

${\mathcal {L}}'=\partial ^{\mu }\phi \partial _{\mu }\phi -2\lambda a^{2}\phi ^{2}+{\mathcal {O}}(\phi ^{3})=\partial ^{\mu }\phi \partial _{\mu }\phi -m^{2}\phi ^{2}+{\mathcal {O}}(\phi ^{3})$,

где $m={\sqrt {2\lambda ^{2}a^{2}}}={\sqrt {-2\mu ^{2}}}$. В этом примере необходимо выделить ещё одну важную деталь. Лагранжиан ${\mathcal {L}}$ описывает безмассовое поле $\varphi$ с потенциалом взаимодействия $V=\mu ^{2}\varphi ^{2}+1/2\lambda ^{2}\varphi ^{4}$. Безмассовость поля $\varphi$ состоит в том, что знак $\mu ^{2}<0$ совпадает со знаком кинетической энергии, а потому не может отвечать за массу. Однако уже лагранжиан ${\mathcal {L}}'$ описывает свободное поле Клейна — Гордона с массой $m={\sqrt {-2\mu ^{2}}}$. Таким образом спонтанное нарушение симметрии может генерировать массу поля. Далее это явление будет исследовано более детально.

Калибровочные преобразования образуют группу Ли, причем компактную. Рассмотрим лагранжиан

${\mathcal {L}}={\frac {1}{2}}\partial ^{\mu }\varphi _{i}\partial _{\mu }\varphi ^{i}-V(\varphi _{i})$,

где $\varphi _{i}$ — N скалярных вещественных полей. Допустим лагранжиан инвариантен относительно преобразований $\omega _{i}^{j}$ калибровочной группы $G$

$\varphi _{i}=\omega _{i}^{j}\varphi _{j}$.

Случай инвариантного вакуума

Если потенциал $V$ имеет минимум в точке $\varphi _{i}=0$, то можно показать, что вакуум является инвариантным относительно всех калибровочных преобразований, а именно, что действие любой матрицы на нулевой вектор переводит его в нулевой вектор. В таком случае можно разложить потенциал в ряд Тейлора в окрестности нуля. Предполагая, что $V(0)=0$, а также учитывая, что первые производные в точке экстремума равны нулю, а матрица вторых производных $(m^{2})^{ij}={\frac {\partial ^{2}V}{\partial \varphi _{i}\partial \varphi _{j}}}(0)$ в точке минимума является положительно определённой, получим

${\mathcal {L}}={\frac {1}{2}}\partial ^{\mu }\varphi _{i}\partial _{\mu }\varphi ^{i}-{\frac {1}{2}}(m^{2})^{ij}\varphi _{i}\varphi _{j}+{\mathcal {O}}(\varphi ^{3})$.

При соответствующем ортогональном преобразованиеи $\varphi _{i}'=O_{i}^{j}\varphi _{j}$ массовую матрицу $m^{2}$ можно привести к диагональному виду. Таким образом полученный лагранжиан описывает $N$ действительных скалярных полей с массами, которые определяются собственными значениями матрицы $m^{2}$.

Случай неинвариантного вакуума

Совсем иная ситуация, когда потенциал $V$ имеет минимум не в нуле. Это соответствует свободе в выборе вакуумного состояния. Вакуум будет инвариантный только в отношении определённой подгруппы $H$ калибровочной группы $G$. группу $H\subset G$ называют малой группой. Происходит нарушение локальной симметрии калибровочной группы $G$. Рассмотрим пример нарушения глобальной симметрии, которая задается калибровочной группой трехмерных поворотов $SO(3)$ (SO(3)), в линейной сигма-модели.

Пример 2. Нарушение глобальной калибровочной симметрии SO (3)

Пусть лагранжиан

${\mathcal {L}}={\frac {1}{2}}\partial ^{\mu }\varphi _{i}\partial _{\mu }\varphi ^{i}-{\frac {1}{2}}\lambda \left(\varphi _{i}\varphi ^{i}-a^{2}\right)^{2}$,

где присутствуют три скалярных поля $\varphi _{i}$. Этот лагранжиан называют линейной сигма-моделью, которая является инвариантной относительно преобразований группы $SO(3)$ (ортогональные матрицы с единичным определителем). На вектор $\varphi =\mid \mid \varphi _{1},\;\varphi _{2},\;\varphi _{3}\mid \mid ^{T}$ элементы группы действуют как матрицы трехмерных поворотов. Вакуум этого поля вырожденный и лежит на точке сферы

$\varphi _{1}^{2}+\varphi _{2}^{2}+\varphi _{3}^{2}=a^{2}$.

Соответствующими преобразованиями системы координат всегда можно представить вакуум в виде

$\varphi _{0}=\mid \mid 0,\;0,\;a\mid \mid ^{T}$.

Очевидно, что вакуум не является инвариантным относительно $SO(3)$, однако он инвариантен относительно группы $SO(2)\subset SO(3)$ поворотов вокруг оси $\varphi _{3}$. Разложим поле в окрестности вакуума $\varphi =\varphi _{0}+\phi (x)$, считая $\phi (x)$ малой величиной. Лагранжиан при этом представляется в виде

${\mathcal {L}}'={\frac {1}{2}}(\partial ^{\mu }\phi _{1})^{2}+{\frac {1}{2}}(\partial ^{\mu }\phi _{2})^{2}+{\frac {1}{2}}(\partial ^{\mu }\phi _{3})^{2}-2\lambda a^{2}\phi _{3}^{2}+{\mathcal {O}}(\phi ^{3})$,

что соответствует двум безмассовых скалярным полям $\phi _{1}$, $\phi _{2}$ и полю $\phi _{3}$ с массой $m=2{\sqrt {\lambda }}a$. Как видим нарушение глобальной калибровочной симметрии может генерировать массу поля.

В общем можно показать, что имеет место следующая теорема

Теорема Голдстоуна. При спонтанном нарушении глобальной калибровочной симметрии возникают $\dim G-\dim H$ безмассовых скалярных полей $\phi _{i}$ и $N-(\dim G-\dim H)$ массивных скалярных полей ${\tilde {\phi }}_{i}$. Здесь $N$ является размерностью избранного представления $G$ (фактически начальное количество действительных скалярных полей).

При этом безмассовые поля, которые возникают при спонтанном нарушении глобальной калибровочной симметрии называются бозонами Голдстоуна. Ещё раз подчеркнем, что их количество равно количеству нарушенных симметрий.

Пример 3. Нарушение глобальной калибровочной симметрии SO(N)

Рассмотрим, как в предыдущем примере, лагранжиан вида

${\mathcal {L}}={\frac {1}{2}}\partial ^{\mu }\varphi _{i}\partial _{\mu }\varphi ^{i}-{\frac {1}{2}}\lambda \left(\varphi _{i}\varphi ^{i}-a^{2}\right)^{2},$

где присутствуют уже $N$ действительных скалярных полей $\varphi _{i}$. Эта модель является инвариантной относительно преобразований группы $SO(N)$.

При нарушении симметрии вакуум будет инвариантным относительно группы $SO(N-1)\subset SO(N)$. Размерность группы $SO(N)$ равна $\dim SO(N)=N(N-1)/2$. Следовательно число бозонов Голдсоуна, которые образуются при спонтанном нарушении локальной симметрии равно $\dim SO(N)-\dim SO(N-1)=N-1$. Тогда при спонтанном нарушении глобальной симметрии $SO(N)$ возникают $N-1$ бозонов Голдстоуна и один массивный бозон.

В случае $N=3$ по теореме Голдстоуна получаем 2 голдстоуновских бозонов и одно массивное поле, что было непосредственно проверено в предыдущем примере.

Доказательство теоремы Голдстоуна

Генераторы малой группы обозначим как $t_{H,a}$ для фундаментального представления группы $G$ или для любого другого представления $T_{H,a}$. Тогда из условия инвариантности вакуума следует, что $\exp {(-ie\alpha ^{a}T_{H,a})}\varphi _{0}=\varphi _{0}$. Раскладывая функцию в ряд Тейлора, получим, что действие генераторов малой ненарушенной группы на вакуум уничтожает вакуум

$T_{H,a}\varphi _{0}=0$.

Это условие является важным критерием ненарушенной симметрии.

Остальные генераторы группы $G$ обозначим как $t_{G/H,a}$ (или $T_{G/H,a}$). Их воздействие на вакуум не даёт ноль, иначе сгенерированные ими преобразования оставляли бы вакуум инвариантным и принадлежали малой группе. Введём векторы $E_{k}=-iT_{G/H,k}\varphi _{0}$. Их количество $\dim G-\dim H$. Они линейно независимы и образуют базис в подпространстве голдстоуновских бозонов (нарушенных симметрий).

Во всем пространстве удобно ввести ортогональный базис $\{e_{k},{\widetilde {e}}_{k}\}$, где векторы $e_{k}$ — орты голдстоуновского подпространства и составленные из линейных комбинаций векторов $E_{k}$, а $N-(\dim G-\dim H)$ векторов ${\widetilde {e}}_{k}$ образуют базис остального пространства. Тогда скалярные поля можно разложить в таком базисе

$\varphi _{i}=\varphi _{0i}+\phi _{k}(e^{k})_{i}+{\widetilde {\phi }}_{k}({\widetilde {e}}^{k})_{i}$,

а лагранжиан в квадратичном приближении примет вид

${\mathcal {L}}={\frac {1}{2}}\partial ^{\mu }\phi _{i}\partial _{\mu }\phi ^{i}+{\frac {1}{2}}\partial ^{\mu }{\widetilde {\phi _{i}}}\partial _{\mu }{\widetilde {\phi }}^{i}-{\frac {1}{2}}{\frac {\partial ^{2}V(\varphi _{0})}{\partial \varphi _{i}\partial \varphi _{j}}}(\phi _{k}e^{k}+{\widetilde {\phi }}_{k}{\widetilde {e}}^{k})_{i}(\phi _{k}e^{k}+{\widetilde {\phi }}_{k}{\widetilde {e}}^{k})_{j}+{\mathcal {O}}(\phi ^{3})$,

из которого явно не видно выполнения теоремы Голдстоуна. Однако из условия калибровочной инвариантности минимума потенциала (не следует путать с вакуумом, речь идет об инвариантности значения потенциала и его производных)

${\frac {\partial V}{\partial \varphi _{j}}}(\exp {(-ie\alpha ^{a}T_{a})}\varphi _{0})=0\Rightarrow _{\alpha \rightarrow 0}-ie\alpha ^{a}(T_{a}\varphi _{0})_{i}{\frac {\partial ^{2}V(\varphi _{0})}{\partial \varphi _{i}\varphi _{j}}}=0$.

Для ненарушенной симметрии верно равенство $T_{H,a}\varphi _{0}=0$, однако для нарушенных симметрий соотношение $-iT_{G/H,a}\varphi _{0}=E_{a}\neq 0$, а учитывая, что из линейных комбинаций $E_{a}$ получаем базис $e_{a}$ следует $e_{i}^{a}{\frac {\partial ^{2}V(\varphi _{0})}{\partial \varphi _{i}\partial \varphi _{j}}}=0.$ Поэтому лагранжиан ${\mathcal {L}}$ представим в виде

${\mathcal {L}}={\frac {1}{2}}\partial ^{\mu }\phi _{i}\partial _{\mu }\phi ^{i}+{\frac {1}{2}}\partial ^{\mu }{\widetilde {\phi _{i}}}\partial _{\mu }{\widetilde {\phi }}^{i}-{\frac {1}{2}}(m^{2})^{kl}{\widetilde {\phi }}_{k}{\widetilde {\phi }}_{l}+{\mathcal {O}}(\phi ^{3})$,

где массы $(m^{2})^{kl}=({\widetilde {e}}^{k})_{i}({\widetilde {e}}^{l})_{j}{\frac {\partial ^{2}V(\varphi _{0})}{\partial \varphi _{i}\varphi _{j}}}$. Этот вывод доказывает теорему Голдстоуна. Фактически это рассмотрение спонтанного нарушения симметрии в общем случае, который можно легко провести в случае конкретной симметрии как в примерах.

Нарушение локальной калибровочной симметрии

Основная статья: Механизм Хиггса

Рассмотренная выше теорема Голдстоуна утверждает, что при нарушении калибровочной симметрии возникают безмассовые безспиновые бозоны. Из-за отсутствия таких частиц в природе, теорема Голдстоуна рассматривалась в качестве контраргумента против нарушенных симметрий. Однако, как оказалось, когда нарушается локальная, а не глобальная калибровочная симметрия, то безмассовые голдстоуновские бозоны отсутствуют, а вместо этого калибровочные векторные поля получают массу. Спонтанное нарушение локальной калибровочной симметрии является важным явлением в теории поля, поскольку оно ведет к появлению у калибровочных полей масс (напомним, что сами по себе массовые слагаемые для калибровочного поля является калибровочно-инвариантными, поэтому в лагранжиане поля с ненарушенной симметрией они отсутствуют). Такой механизм носит название механизма генерации масс Хиггса.

Локальные преобразования отличаются от глобальных наличием координатной зависимости $\alpha =\alpha (x)$. Такая зависимость приводит к возникновению в лагранжиане калибровочных полей (в случае заряженного поля Клейна — Гордона — электромагнитного поля с группой симметрии $U(1)$. При рассмотрении трехкомпонентного вектора скалярных полей с группой симметрии $SU(3)$ — калибровочного поля, которое можно отождествить с цветовым глюонным полем сильного ядерного взаимодействия и т. д.).

Рассмотрим лагранжиан

${\mathcal {L}}={\frac {1}{2}}{\mathcal {D}}^{\mu }\varphi _{i}{\mathcal {D}}_{\mu }\varphi ^{i}-V(\varphi _{i})-{\frac {1}{4}}F_{\mu \nu }^{a}F_{a}^{\mu \nu }$,

где $\varphi _{i}$ — набор $N$ скалярных полей, $F_{\mu \nu }^{a}=\partial _{\mu }A_{\nu }^{a}-\partial _{\nu }A_{\mu }^{a}+\left[A_{\mu },A_{\nu }\right]^{a}$ — тензор соответствующего калибровочного поля, ${\mathcal {D}}_{\mu }\varphi _{i}=\partial _{\mu }\varphi _{i}+(A_{\mu })_{i}^{j}\varphi _{j}$ — ковариантная производная. Векторный потенциал в общем случае является матрицей, которая действует на векторный столбец $\varphi =\mid \mid \varphi _{1},\varphi _{2},...,\varphi _{N}\mid \mid ^{T}$). Индекс $a$ пробегает значения от 1 до $\dim G$ и нумерует компоненты потенциала по генераторам группы симметрии. Этот лагранжиан инвариантен относительно локальных калибровочных преобразований $\omega _{j}^{i}=\omega _{j}^{i}(x),$ образующих группу $G$. Поля при калибровочных преобразованиях преобразуются следующим образом

$\varphi _{i}\rightarrow \omega _{i}^{j}\varphi _{j},\qquad A_{\mu }\rightarrow \omega A_{\mu }\omega ^{-1}+\omega \partial _{\mu }\omega ^{-1}$.

Случай инвариантного вакуума

Если минимум $V$ реализуется при $\varphi _{i}=0$, то в таком случае можно разложить лагранжиан в ряд Тейлора в окрестности вакуума и получить в квадратичном приближении лагранжиан

${\textstyle {\mathcal {L}}={\frac {1}{2}}\partial ^{\mu }\varphi _{i}\partial _{\mu }\varphi ^{i}-{\frac {1}{2}}(m^{2})^{ij}\varphi _{i}\varphi _{j}-{\frac {1}{4}}(\partial _{\mu }A_{\nu }^{a}-\partial _{\nu }A_{\mu }^{a})^{2}+{\mathcal {O}}(\varphi ^{3},\varphi ^{2}A,\varphi A^{2},A^{3}),}$

который описывает $N$ массивных скалярных полей, и $\dim G$ безмассовых калибровочных векторных полей $A_{\mu }^{a}$. Вычислим число полевых степеней свободы набора этих полей. Поскольку скалярное поле имеет одну степень свободы, а безмассовых векторное поле — две, то суммарное количество степеней свободы равно $N+2\dim G$.

Случай неинвариантного вакуума

Основное отличие локальной калибровочной симметрии от глобальной заключается в зависимости калибровочной константы $\alpha$ от координат $x^{\mu }$. Эта координатная зависимость позволяет соответствующим выбором $\alpha (x)$ занулить поля $\varphi _{i}$ всех $\dim G-\dim H$ безмассовых голдстоуновских бозонов во всем пространстве. Такая калибровка называется унитарной (можно показать, что она всегда существует в случае компактных калибровочных групп). Однако эта калибровка приводит к появлению в лагранжиан массовых слагаемых типа $a^{2}A^{\mu }A_{\mu }$, которые, тем не менее, являются калибровочно инвариантными. При унитарной калибровке массовые слагаемые возникают ровно для $\dim G-\dim H$ калибровочных полей. Поскольку унитарной калибровкой уничтожаются бозоны Голдстоуна, и возникают массивные калибровочные бозоны, то часто говорят, что векторные поля «съедают» бозоны Голдстоуна и приобретают массы. Условие унитарной калибровки записывают через «матричные элементы» генераторов нарушенной симметрии в виде

$\varphi _{0}T_{G/H,a}\varphi =0$.

Эта формула означает, что поле $\varphi$ ортогонально ко всем векторам $E_{k}=-iT_{G/H,k}\varphi _{0}$ пространств нарушенных симметрий. Также при спонтанном нарушении симметрии возникают $N-(\dim G-\dim H)$ массивных скалярных поля, называемых бозонами Хиггса. Количество полей, получаемых в результате спонтанного нарушения локальной калибровочной симметрии определяется

Теорема Хиггса. При спонтанном нарушении локальной калибровочной симметрии присутствуют $N-(\dim G-\dim H)$ массивных скалярных полей (бозонов Хиггса), $\dim G-(\dim G-\dim H)=\dim H$ безмассовых векторных полей, а также $\dim G-\dim H$ массивных векторных полей (количество массивных калибровочных бозонов равно количеству нарушенных симметрий).

Теперь найдём количество полевых переменных в этой системе. Учитывая, что массивное поле имеет три степени свободы, суммарное количество полевых степеней свободы равно $N-(\dim G-\dim H)+2\dim H+3(\dim G-\dim H)=N+2\dim G$, что совпадает с результатом для инвариантного вакуума.

Пример 4. Нарушение локальной калибровочной симметрии SO (3)

Рассмотрим лагранжиан

${\mathcal {L}}={\frac {1}{2}}{\mathcal {D}}^{\mu }\varphi _{i}{\mathcal {D}}_{\mu }\varphi ^{i}-{\frac {\lambda }{2}}\left(\varphi _{i}\varphi ^{i}-a^{2}\right)^{2}-{\frac {1}{4}}F_{\mu \nu }^{a}F_{a}^{\mu \nu }$,

где индекс $i$ принимает значения между 1 и 3. Вакуумное состояние выберем в виде $\varphi _{0}=\mid \mid 0;0;a\mid \mid ^{T}$. Аналогично другим примерам разложим полевые функции в окрестности вакуума $\varphi =\varphi _{0}+\phi$. В квадратичном приближении по полю лагранжиан перепишется в виде

${\mathcal {L}}={\frac {1}{2}}(\partial ^{\mu }\phi _{3})^{2}-2\lambda a^{2}(\phi _{3})^{2}-{\frac {1}{4}}\left(\partial _{\mu }A_{\nu }^{a}-\partial _{\nu }A_{\mu }^{a}\right)^{2}+{\frac {1}{2}}\left(\partial _{\mu }\phi _{1}-eaA_{\mu }^{2}\right)^{2}+{\frac {1}{2}}\left(\partial _{\mu }\phi _{2}+eaA_{\mu }^{1}\right)^{2}+{\mathcal {O}}(\phi ^{3},\phi ^{2}A,\phi A^{2},A^{3})$.

Полученный лагранжиан диагонализуем с помощью замены переменных

$B_{\mu }^{1}=A_{\mu }^{1}+{\frac {1}{ea}}\partial _{\mu }\phi _{2},\qquad B_{\mu }^{2}=A_{\mu }^{2}-{\frac {1}{ea}}\partial _{\mu }\phi _{1}$.

Тогда диагонализований лагранжиан имеет вид

${\mathcal {L}}\approx {\frac {1}{2}}(\partial ^{\mu }\phi _{3})^{2}-2\lambda a^{2}(\phi _{3})^{2}-{\frac {1}{4}}\left(\partial _{\mu }A_{\nu }^{3}-\partial _{\nu }A_{\mu }^{3}\right)^{2}-{\frac {1}{4}}\left(\partial _{\mu }B_{\nu }^{1}-\partial _{\nu }B_{\mu }^{1}\right)^{2}+{\frac {e^{2}a^{2}}{2}}(B_{\mu }^{1})^{2}-{\frac {1}{4}}\left(\partial _{\mu }B_{\nu }^{2}-\partial _{\nu }B_{\mu }^{2}\right)^{2}+{\frac {e^{2}a^{2}}{2}}(B_{\mu }^{2})^{2}$.

Как видим, полученный в результате спонтанного нарушения симметрии лагранжиан описывает одно скалярное поле $\phi _{3}$ с массой $m_{\phi }=2a{\sqrt {\lambda }}$, одно безмассовое векторное поле $A^{3}$ и два массивных векторные поля $B^{2},\;B^{3}$ с массами $m_{B}=ea$, что находится в полном соответствии с общими соображениями, приведенными выше.

Стоит отметить, что унитарная калибровка оставляет определённую симметрию в лагранжиане. Группой этой симметрии является малая группа $H$. В случае нарушения $SO(3)$ симметрии (пример выше) малой группой является группа поворотов $SO(2)$ относительно оси $\phi _{3}$. Заметим, что группа $SO(2)$ изоморфна группе $U(1)$ калибровочной симметрии электромагнитного поля.

Доказательство теоремы Хиггса

Для доказательства теоремы Хиггса, по аналогии с доказательством теоремы Голдстоуна разложим скалярное поле $\varphi _{i}=\varphi _{0i}+\phi _{k}(e^{k})_{i}+{\widetilde {\phi }}_{k}({\widetilde {e}}^{k})_{i}$. Также разложим калибровочное поле с генераторами калибровочной группы $G$: $A_{\mu }=ie(A_{H,\mu }^{a}t_{H,a}+A_{G/H,\mu }^{a}t_{G/H,a})$. В квадратичном приближении разложение для скалярных полей имеет такой же вид как и в доказательстве теоремы Голдстоуна, квадрат тензора поля $-{\frac {1}{4}}F_{\mu \nu }^{a}F_{a}^{\mu \nu }=-{\frac {1}{4}}\left(\partial _{\mu }A_{\nu }^{a}-\partial _{\nu }A_{\mu }^{a}\right)^{2}$, а ковариантная производная в первом приближении (линейного приближения по отклонениям от вакуума достаточно для получения квадратичного по отклонению лагранжиана) запишется в виде

${\mathcal {D}}_{\mu }\varphi \approx \partial _{\mu }\varphi +A_{\mu }\varphi _{0}=\partial _{\mu }\varphi +ieA_{G/H,\mu }^{a}T_{G/H,a}\varphi _{0}=e^{k}\partial _{\mu }\phi _{k}+{\widetilde {e}}^{k}\partial _{\mu }{\widetilde {\phi }}_{k}-eA_{G/H,\mu }^{a}E_{a}$.

Подстановка данных выражений в полученный лагранжиан даёт в квадратичном по полям приближении лагранжиан

${\mathcal {L}}=-{\frac {1}{4}}\left(\partial _{\mu }A_{\nu }^{a}-\partial _{\nu }A_{\mu }^{a}\right)^{2}+{\frac {1}{2}}(\partial _{\mu }\phi _{k}-eA_{G/H,\mu }^{a}K_{ak})^{2}+{\frac {1}{2}}\partial ^{\mu }{\widetilde {\phi _{i}}}\partial _{\mu }{\widetilde {\phi }}^{i}-{\frac {1}{2}}(m^{2})^{kl}{\widetilde {\phi }}_{k}{\widetilde {\phi }}_{l}+{\mathcal {O}}(\varphi ^{3},\varphi ^{2}A,\varphi A^{2},A^{3})$,

где $K_{ak}=(E_{a})_{i}(e_{k})^{i}$. Матрица $K_{ak}$ является невырожденной, поскольку фактически является матрицей перехода между базисами $E_{a}=K_{ak}e^{k}$. Можно ввести поля $B_{\mu }^{a}=A_{G/H,\mu }^{a}-{\frac {1}{e}}\partial _{\mu }\phi _{k}(K^{-1})^{ka}$$B_{\mu }^{a}=A_{G/H,\mu }^{a}-{\frac {1}{e}}\partial _{\mu }\phi _{k}(K^{-1})^{ka}$ $B_{\mu }^{a}=A_{G/H,\mu }^{a}-{\frac {1}{e}}\partial _{\mu }\phi _{k}(K^{-1})^{ka}$$B_{\mu }^{a}=A_{G/H,\mu }^{a}-{\frac {1}{e}}\partial _{\mu }\phi _{k}(K^{-1})^{ka}$$B_{\mu }^{a}=A_{G/H,\mu }^{a}-{\frac {1}{e}}\partial _{\mu }\phi _{k}(K^{-1})^{ka}$ (это соответствует унитарной калибровке), тогда окончательно лагранжиан запишется в виде

${\mathcal {L}}=-{\frac {1}{4}}\left(\partial _{\mu }A_{H,\nu }^{a}-\partial _{\nu }A_{H,\mu }^{a}\right)^{2}-{\frac {1}{4}}\left(\partial _{\mu }B_{\nu }^{a}-\partial _{\nu }B_{\mu }^{a}\right)^{2}+{\frac {1}{2}}M_{ab}^{2}B_{\mu }^{a}B_{\mu }^{b}+{\frac {1}{2}}\partial ^{\mu }{\widetilde {\phi _{i}}}\partial _{\mu }{\widetilde {\phi }}^{i}-{\frac {1}{2}}(m^{2})^{kl}{\widetilde {\phi }}_{k}{\widetilde {\phi }}_{l}+{\mathcal {O}}(\varphi ^{3},\varphi ^{2}A,\varphi A^{2},A^{3})$,

где $(M^{2})_{ab}=e^{2}K_{ai}K_{bi}$, $(m^{2})^{kl}=({\widetilde {e}}^{k})_{i}({\widetilde {e}}^{l})_{j}{\frac {\partial ^{2}V(\varphi _{0})}{\partial \varphi _{i}\varphi _{j}}}$. Что доказывает формулировку теоремы Хиггса.

Спонтанное нарушение приближенной симметрии

В предыдущих подразделах рассматривалась ситуация, когда финальный лагранжиан обладает определённой симметрией группы $G$, которая спонтанно нарушается. Теперь рассмотрим случай, когда в лагранжиане с симметрией добавляются малые слагаемые, которые разрушают симметрию (иногда наличие малых несимметричных слагаемых в отличие от спонтанного нарушения симметрии называется мягким нарушением симметрии). При спонтанном нарушении приближенной симметрии возникают безспиновые поля малой массы, называемые псевдоголдстоуновскими бозонами.

Пусть потенциальная энергия принимает вид $V(\varphi )=V_{0}(\varphi )+\lambda V_{1}(\varphi )$, где слагаемое $V_{0}(\varphi )$ удовлетворяет условию инвариантности относительно преобразований группы $G$: $(T_{a}\varphi _{0})_{i}{\frac {\partial V_{0}(\varphi _{0})}{\partial \varphi _{i}}}=0$, $V_{1}(\varphi )$ представляет собой возмущение, которое разрушает симметрию, $\lambda$ — малый параметр. Слагаемое $V_{1}(\varphi )$ смещает вакуумное состояние в точку ${\overline {\varphi }}_{0}={\varphi }_{0}+\lambda {\varphi }_{0}^{(1)}$ . Тогда условие минимума запишется в виде

${\frac {\partial V}{\partial \varphi _{i}}}\left(\varphi _{0}+\lambda \varphi _{0}^{(1)}\right)=0\Rightarrow {\frac {\partial V_{0}(\varphi _{0})}{\partial \varphi _{i}}}+\lambda \left[{\frac {\partial V_{1}(\varphi _{0})}{\partial \varphi _{i}}}+{\frac {\partial ^{2}V_{0}(\varphi _{0})}{\partial \varphi _{i}\partial \varphi _{j}}}\varphi _{0,j}^{(1)}\right]=\lambda \left[{\frac {\partial V_{1}(\varphi _{0})}{\partial \varphi _{i}}}+{\frac {\partial ^{2}V_{0}(\varphi _{0})}{\partial \varphi _{i}\partial \varphi _{j}}}\varphi _{0,j}^{(1)}\right]=0.$

Если умножить последнее уравнение на $(T_{a}\varphi _{0})_{i}$ и учитывая, что второе слагаемое даст $0$ (условие инвариантности значения вакуума относительно преобразований калибровочной группы, см. Доказательство теоремы Голдстоуна), получаем

$(T_{a}\varphi _{0})_{i}{\frac {\partial V_{1}(\varphi _{0})}{\partial \varphi _{i}}}=0.$

Полученное уравнение называется условием подстройки вакуума. Если это условие не удовлетворяется, то даже малое возмущение приводит к столь больших изменений ${\overline {\varphi }}_{0}$, что члены разложения ${\overline {\varphi }}_{0}$ в окрестности ${\varphi }_{0}$ не являются малыми поправками. Однако в случае, когда $G$ является компактной группой Ли, это условие выполняется. По аналогии с расписанием в пункте «Доказательство теоремы Голдстоуна» можно получить массовую матрицу псевдоголдстоуновских бозонов

$(m^{2})^{kl}=({e}^{k})_{i}({e}^{l})_{j}{\frac {\partial ^{2}V}{\partial \varphi _{i}\partial \varphi _{j}}}\left(\varphi _{0}+\lambda \varphi _{0}^{(1)}\right)=\lambda ({e}^{k})_{i}({e}^{l})_{j}\left[{\frac {\partial ^{2}V_{1}(\varphi _{0})}{\partial \varphi _{i}\partial \varphi _{j}}}+{\frac {\partial ^{3}V_{0}(\varphi _{0})}{\partial \varphi _{i}\partial \varphi _{j}\partial \varphi _{n}}}\varphi _{0,n}^{(1)}\right].$

Массовая матрица псевдоголдстоуновских бозонов является положительно-определенной.

Нарушение симметрии квантового поля

В квантовой теории полевая переменная $\varphi (x)$ перестает быть просто действительной или комплексной функцией координат, а становится линейным оператором ${\widehat {\Phi }}(x)$ заданном на гильбертовом пространстве состояний поля, в представлении Фока или вторичного квантования имеет вид

$|...,n_{\textbf {k}},...\rangle =C(...,n_{\textbf {k}},...)\prod _{\textbf {k}}b_{\textbf {k}}^{+}|0\rangle ,$

где $C$ — константа нормировки, $b_{\textbf {k}}^{+}$ — оператор рождения, который увеличивает число частиц с определённым импульсом ${\textbf {k}}$ на 1, например для бозонов $b_{\textbf {k}}^{+}|...,n_{\textbf {k}},...\rangle ={\sqrt {n_{\textbf {k}}+1}}|...,n_{\textbf {k}}+1,...\rangle$, $|0\rangle$ — вакуумное состояние, в котором нет никаких частиц (возбуждений). Наблюдаемыми величинами являются средние от полевых операторов на состояниях поля $\langle ...,n_{\textbf {k}},...|{\widehat {A}}|...,n_{\textbf {k}},...\rangle$, где ${\widehat {A}}$ — некоторый оператор, полиномиальный по операторам поля.

Однако можно показать, что среднее от оператора ${\widehat {A}}$ на состояниях $|...,n_{\textbf {k}},...\rangle$ можно переписать через вакуумное среднее $\langle 0|{\widehat {B}}|0\rangle$ от оператора ${\widehat {B}}$, который тоже имеет полиномиальный вид по операторам поля. Такие вакуумные средние удобно вычислять как функциональные производные от так называемого образующего функционала, который обозначается как функциональный интеграл

$Z=\int [d\varphi ][d\psi ][...]e^{iS[\varphi ,\psi ,...]},$

где $S$ — классическое действие для полей $\varphi ,\psi ,...$. Образующий функционал представляет собой амплитуду перехода вакуум-вакуум.

Чаще всего образующий функционал и его производные вычисляют, проводя разложение в окрестности действия свободных невзаимодействующих полей (квадратичный по полям лагранжиан). Поправки к невзаимодействующей теории удобно вычислять с помощью диаграмм Фейнмана.

Как и в квантовой механике по отношению к классической, операторная природа поля приводит к нетривиальным квантовым эффектам. Иногда квантовые поправки незначительны, однако в общем случае, они могут иметь значительный (потенциально бесконечный) вклад. Часто для квантового поля имеют место квантовые аномалии — нарушение симметрийных характеристик квантовой системы, у которых есть классическое соответствие. Поэтому данная в предыдущем разделе физическая картина нарушения симметрии для классического поля не может быть непосредственно экстраполирована на квантовый случай и априори утверждать выполнения теорем Голдстоуна или Хиггса в квантовом случае нельзя.

Глобальная калибровочная симметрия

Теорема Голдстоуна в квантовом случае легко доказана в формализме эффективного действия (потенциала). В рамках этого подхода вводятся дополнительные классические токи $J_{i}(x)$, которые взаимодействуют со скалярными полями $\varphi _{i}(x)$. Образующий функционал можно переписать в виде

$Z[J]=\exp {(iW[J])},$

где величина $W[J]$ — сумма всех связных вакуумных диаграмм, причём диаграммы которые образуются друг из друга перестановкой вершин разными ни считаются. Вакуумные средние значения полевых операторов $\varphi _{J}^{i}(x)=\langle \Phi ^{i}(x)\rangle _{0,J}$ при заданных классических токах $J_{i}(x)$ переписываются через вариационные производные от $W[J]$

$\varphi _{J}^{i}(x)={\frac {\delta }{\delta J_{i}(x)}}W[J].$

Обозначим ток $J_{i}(x)$, для которого вакуумное полевое среднее равно заранее заданному полю $\varphi _{J}^{i}=\varphi ^{i}$. Преобразование Лежандра от $W[J]$ приводит к квантовому эффективному действию $\Gamma [\varphi ]$

$\Gamma [\varphi ]=-\int d^{4}x\varphi ^{i}(x)J_{i,\varphi }(x)+W[J].$

величина $\Gamma [\varphi ]$ является суммой всех связанных одночастичных неприводимых диаграмм при наличии тока $J_{i}(x)$. Можно показать, что

${\frac {\delta \Gamma [\varphi ]}{\delta \varphi ^{i}(x)}}=-J_{i}(x).$

При отсутствии внешних токов $J_{i}(x)=0$, значения вакуумных средних определяются как стационарные точки функционала

${\frac {\delta \Gamma [\varphi ]}{\delta \varphi ^{i}(x)}}=0.$

Эффективное действие $\Gamma [\varphi ]$ учитывает квантовые поправки всех порядков, при этом обеспечивая классическую трактовку поля вакуумных средних $\varphi _{i}(x)$ полевых операторов. Если принять, что вакуум является инвариантным относительно преобразований Лоренца трансляций и поворотов, то можно показать, что эффективное действие записывается в виде

$\Gamma [\varphi ]=-{\mathcal {V}}_{4}V(\varphi ),$

где ${\mathcal {V}}_{4}$ — объём пространства-времени, а $V(\varphi )$ — обычная функция, которая называется эффективным потенциалом.

Согласно тождествами Славнова — Тейлора эффективное действие инвариантно относительно инфинитезимальных преобразований вакуумных полей $\delta _{\varepsilon }\varphi ^{i}(x)=\varepsilon \langle F^{i}(x)\rangle _{J}$ (здесь под $\varphi ^{i}(x)$ имеется в виду любое поле, а не только скалярное). Для широкого класса так называемых линейных инфинитезимальных преобразований (к которым относятся и калибровочные преобразования)

$F^{i}(x)=s^{i}(x)+A_{j}^{i}\varphi ^{j}(x),$

где $A_{j}^{i}$ — постоянная матрица, эффективное действие инвариантно относительно тех же симметрий, что и исходное классическое действие. Таким образом, если такая симметрия не нарушена на классическом уровне, то она не будет нарушена квантовыми поправками в любом порядке теории возмущений.

С помощью эффективного потенциала доказательство теоремы Голдстоуна в квантовом случае можно провести используя почти такие же соображения как и для классических полей (с точностью до замены потенциала на эффективный потенциал и классических полей на вакуумные средние полевых операторов). В квантовой теории поля значение квадратов масс бозонов после нарушения симметрии определяются собственными значениями массовой матрицы $(m^{2})_{ij}={\frac {\partial ^{2}V}{\partial \varphi ^{i}\partial \varphi ^{j}}}$. А поскольку, как было сказано выше, симметрия эффективного действия (потенциала) относительно калибровочных преобразований такая же как и исходного действия, то количество нулевых собственных значений квантовой массовой матрицы такая же как и для классической, а теорема Голдстоуна выполняется и в квантовом случае.

Локальная калибровочная симметрия

В квантовой теории поля, теорема Хиггса остается справедливой, хотя по причинам приведеным в начале раздела, математическое рассмотрение проблемы является сложным. Для удаления «нефизических» голдстоуновских мод при рассмотрении нарушения локальной калибровочной симметрии классического поля использовалось унитарная калибровка. Однако при применении унитарной калибровки в квантовой теории поля оказывается, что пропагатор калибровочного поля имеет асимптотическое поведение ${\mathcal {O}}(1)={\mathcal {O}}(k^{0})$, а потому просто проверить теорию на перенормируемость (подсчетом степеней) не удается. В квантовой теории поля используется зависящее от действительного параметра $\xi$ так называемое $R_{\xi }$ -калибровка, которая является обобщением унитарной калибровки. Преимуществом семейства таких калибровок является асимптотика ${\mathcal {O}}(k^{-2})$ пропагатора калибровочного поля.

Так или иначе, выбор калибровки накладывают дополнительные условия на полевые переменные, которые нужно учитывать при квантовании. В теории поля такие условия учитываются в рамках метода Фаддеева — Попова. Рассмотрим лагранжиан

${\mathcal {L}}={\frac {1}{2}}{\mathcal {D}}_{\mu }\varphi {\mathcal {D}}^{\mu }\varphi -V(\varphi )-{\frac {1}{4}}(F_{\mu \nu }^{a})^{2}.$

Раскладывая скалярные поля в окрестности минимума $\varphi (x)=\varphi _{0}+\phi (x)$ можно переписать лагранжиан как функцию $A,\;\phi$ : ${\mathcal {L}}(A,\phi )$. При этом калибровка фиксируется условием $\partial ^{\mu }A_{\mu }^{a}-\xi e\phi _{i}(K^{-1})^{ai}=0$, матрица $K^{ai}$ была введена в предыдущем разделе при рассмотрении доказательства теоремы Хиггса в классическом случае. Всего таких условий $\dim G-\dim H$. Введем функции $G^{a}={\frac {1}{\sqrt {\xi }}}(\partial ^{\mu }A_{\mu }^{a}-\xi g\phi _{i}(K^{-1})^{ai})$, которые будут учитывать калибровки. При $\xi \rightarrow 0$$R_{\xi }$ -калибровка переходит в калибровку Ландау $\partial _{\mu }A_{a}^{\mu }=0$. Унитарная калибровка получается у границы $\xi \rightarrow \infty$.

Квантование теории задаётся с помощью образующего функционала

$Z=C\int ({\mathcal {D}}A)({\mathcal {D}}\phi )\exp \left[i\int d^{4}x({\mathcal {L}}(A,\phi )-{\frac {1}{2}}G^{2})\right]\det \left({\frac {\delta G}{\delta \alpha }}\right),$

где $\alpha$ — калибровочные параметры нарушенных симметрий. В итоге квадратичный по полям лагранжиан принимает вид

${\mathcal {L}}\approx -{\frac {1}{2}}A_{\mu }^{a}\left(\delta ^{ab}\left[-\eta ^{\mu \nu }\partial ^{2}+(1-{\frac {1}{\xi }}\partial ^{\mu }\partial ^{\nu })\right]-\eta ^{\mu \nu }(m_{A}^{2})_{ab}\right)A_{\nu }^{b}+{\frac {1}{2}}(\partial _{\mu }\phi )^{2}-{\frac {1}{2}}(m_{G}^{2})_{ij}\phi _{i}\phi _{j}+{\frac {1}{2}}(\partial _{\mu }{\widetilde {\phi }})^{2}-{\frac {1}{2}}(m_{H}^{2})_{ij}{\widetilde {\phi }}_{i}{\widetilde {\phi }}_{j},$

где матрицы принимают вид $(m_{A}^{2})_{ab}=g^{2}K_{ai}K_{bi}$, $(m_{G}^{2})_{ij}=\xi g^{2}K_{ia}K_{ja}$, $(m_{H}^{2})_{ij}=({\widetilde {e}}^{k})_{i}({\widetilde {e}}^{l})_{j}{\frac {\partial ^{2}V(\varphi _{0})}{\partial \varphi _{i}\varphi _{j}}}+\xi g^{2}K_{ia}K_{ja}$.

Определитель под интегралом можно учесть, добавив к лагранжиану системы лагранжиан духов Фаддеева — Попова:${\mathcal {L}}_{gh}={\overline {c}}\left(-\partial ^{2}-\xi m_{A}^{2}{\frac {\phi (x)}{\varphi _{0}}}\right)c$ .

Наличие масс у голдстоуновских бозонов (которые однако пропорциональны $\sim {\sqrt {\xi }}$) и $\xi$ -зависимость масс бозонов Хиггса зависят от калибровки, что означает их нефизичность. Если их не учитывать, то полученные массовые матрицы показывают полное соответствие между квантовой и классической теоремами Хиггса. Однако сами значения масс могут несколько меняться вследствие квантовых поправок.

Пи-мезоны как псевдоголдстоуны

В качестве примера нарушения симметрии в квантовой теории поля рассмотрим нарушения киральной симметрии $SU(2)\times SU(2)$ квантовой хромодинамики с безмассовыми кварками. Фермионный лагранжиан безмассовых кварков имеет вид

${\mathcal {L}}=i{\overline {u}}\gamma ^{\mu }{\mathcal {D}}_{\mu }u+i{\overline {d}}\gamma ^{\mu }{\mathcal {D}}_{\mu }d,$

где черта над полем означает дираковское сопряжения ${\overline {u}}=u^{\dagger }\gamma ^{0}$, спиноры $u,\,d$ соответствуют $u,\,d$ -кваркам. Вообще говоря, спиноры кварков образуют цветовые триплеты, однако в явном виде записывать их здесь не будем. Такой безмассовый лагранжиан инвариантен относительно преобразований группы $SU(2)\times SU(2)$ изоспинового дублета

$\left|\left|{\begin{array}{c}u\\d\end{array}}\right|\right|\rightarrow \exp {\left(i\alpha _{V}^{a}{\frac {\sigma _{a}}{2}}+i\alpha _{A}^{a}\gamma ^{5}{\frac {\sigma _{a}}{2}}\right)}\left|\left|{\begin{array}{c}u\\d\end{array}}\right|\right|,$

где $t_{a}={\frac {\sigma _{a}}{2}}$, а $\sigma _{a}$ — матрицы Паули. Данной симметрии соответствуют векторный и аксиальный токи симметрии

$V_{a}^{\mu }=i{\overline {q}}\gamma ^{\mu }t_{a}q,\quad A_{a}^{\mu }=i{\overline {q}}\gamma ^{\mu }\gamma _{5}t_{a}q,$

с соответствующими уравнениеми непрерывности $\partial _{\mu }V_{a}^{\mu }=0,\,\partial _{\mu }A_{a}^{\mu }=0$, где $q=||u,d||^{T}$ обозначает изоспиновый кварковый дублет. Соответствующие заряды симметрии ${\widehat {I}}_{a}=\int d^{3}xV_{a}^{0},\;{\widehat {X}}_{a}=\int d^{3}xA_{a}^{0}$ являются генераторами изоспиновой и остаточной симметрий. Действуя на кварковые поля, эти операторы индуцируют преобразования

$[{\widehat {I}}_{a},q]=-t_{a}q,\;[{\widehat {X}}_{a},q]=-\gamma ^{5}t_{a}q$ .

если симметрия $SU(2)\times SU(2)$ является ненарушенной, то каждому адрону соответствует аналог с теми же квантовыми числами (спином, барионным зарядом), но с противоположной четностью. Однако вырождения адронного спектра по четности не наблюдается, поэтому следует предположить, что киральная симметрия с генераторами $X_{a}$ нарушена.

Следует однако заметить, что из-за наличия в лагранжиане массовых слагаемых $-m_{u}{\overline {u}}u-m_{d}{\overline {d}}d$ симметрия $SU(2)\times SU(2)$ является приближенной. Поэтому, как было показано в предыдущем разделе, в спектре частиц возникают псевдоголдстоуновские бозоны с малой массой. Они должны быть безспиновыми, иметь нулевой барионный заряд, с изоспином равным 1 и отрицательной четностью. Легкими среди всех адронов являются именно $\pi$ -мезоны, более того они обладают необходимыми квантовыми числами. Можно показать, что квадрат массовой матрицы $\pi$ мезонов $m_{\pi }^{2}\sim (m_{u}+m_{d})$ и дает массу $\pi$ -мезона 140 МэВ при $m_{u}+m_{d}\sim$ 10 МэВ, что соответствует реальности.

Поле Хиггса и динамическое нарушение симметрии

Динамическое нарушение симметрии заключается в нарушении симметрии квантовыми эффектами поляризации вакуума. Такие поляризационные эффекты нарушают первоначальную классическую калибровочную симметрию группы $G$, редуцируя её к симметрии с малой группой $H$. Поляризация вакуума может приводить к приобретению исходно безмассовыми частицами масс. В такой идеологии бозон Хиггса вводится в теорию следующим образом. Пусть имеем систему материальных и калибровочных полей, которые обозначим для удобства другой буквой $\varphi$. Пусть соответствующее действие $S[\varphi ]$ инвариантно относительно преобразований калибровочной группы $G$. Введем в систему классическое внешнее поле Хиггса $\sigma$, которое редуцирует калибровочную симметрию к малой группы $H$, действие такой системы запишем $S[\varphi ,\sigma ]$. Образующий функционал запишем в следующем виде с интегрированием только по полям $\varphi$, считая поле $\sigma$ заданным

$Z_{\sigma }=\int [d\varphi ]e^{iS[\varphi ,\sigma ]}$.

Теперь к действию $S[\varphi ,\sigma ]$ добавим «затравочное» действие для Хиггсового поля $S_{\sigma }$, а в образующем функционале добавим интегрирование по полям $\sigma$

$Z=\int [d\varphi ][d\sigma ]e^{iS[\varphi ,\sigma ]+iS_{\sigma }}$.

Интегрирование по полям $\varphi$ генерирует некоторое эффективное действие для поля Хиггса

$Z=\int [d\varphi ][d\sigma ]e^{iS[\varphi ,\sigma ]+iS_{\sigma }}=\int [d\sigma ]e^{iS_{eff}+iS_{\sigma }}$.

Преимуществом такого подхода является получение нетривиального вклада в Хиггсове поле, которое происходит от начальной системы полей $\varphi$. Аналогичными методами в квантовой электродинамике получают нелинейные поправки к лагранжиану.

Нарушение симметрии в статистической физике

Различные статистические системы можно представлять как некоторые квантованные поля, так система бозе-частиц (например $^{4}He$) представляет собой комплексное скалярное поле, ферми-система ($^{3}He$) представляется как спинорное поле, однако чаще всего в квантовой статистической физике лагранжиан — эффективный и феноменологический, а соответствующие поля описывают определённые возбуждения в системе (теория Гинзбурга — Ландау, плазмоны, фононы, экситоны и т. д.).

Математический аппарат квантовой теории поля применяется к изучению статистических систем многих частиц. При этом в статистической физике термины квантовой теории поля имеют свои аналоги. Так, например, аналогом образующего функционала является статистическая сумма, которую представляют как функциональный интеграл

$Z=e^{-\beta F[\varphi ]}=\int ({\mathcal {D}}\varphi )\exp {\left(-\beta \int d^{3}x\left[e(x)-\mu (T)\varphi ^{\dagger }\varphi \right]\right)},$

где $F$  — свободная энергия Гельмгольца, которая имеет смысл аналога классического действия в квантовой теории поля, $\varphi$  — совокупность полей модели, $\beta ={\frac {1}{T}}$  — обратная температура, $e(x)$  — плотность энергии в окрестности точки $x$, $\mu$  — химический потенциал.

Понятно, что, как в случае квантовой теории поля, при квантовании статистической системы возникают квантовые поправки, которые могут иметь какое угодно влияние на систему. Однако по аналогии с предыдущим разделом можно ввести эффективный потенциал, который удобно использовать для исследования системы. Если этого достаточно, то можно работать в приближении среднего поля, в рамках которого предполагается

$F\approx E=\int d^{3}x\left[e(x)-\mu \varphi ^{\dagger }\varphi \right].$

Фазовые переходы как спонтанное нарушение симметрии

При изменении температуры меняется и плотность энергии системы (через изменение потенциала взаимодействия) и химический потенциал, поэтому может случиться, что при температурах выше определённой критической температуры $T_{c}$ минимум энергии находится при одной конфигурации системы, а ниже — при другой (или наоборот). Система переходит из состояния, которое уже не является стабильным при данной температуре, в новое стабильное состояние. Макроскопически наблюдается фазовый переход.

Поля отклонения от вакуумного состояния отождествляют с термодинамическими флуктуациями. При спонтанном нарушении симметрии в статистической физике, кроме массивных скаляров, всегда возникают безмассовая моды флуктуаций, которые называют бозонами Голдстоуна (часто Намбу — Голдстоуна). Наличие безмассовых голдстоуновских мод ведет к бесщелевому энергетическому спектру системы (теорема Гугенгольца — Пайнса). Голдстоуновская мода также отвечает за коррелированные во всей системе флуктуации (так называемый недиагональный дальний порядок, например в случае бозе-смеси — бозе-конденсат). Иногда необоснованно в физике конденсированного состояния массивные моды колебаний называют бозонами Хиггса.

Почти все фазовые переходы можно трактовать как спонтанное нарушение симметрии. Тем не менее существуют состояния вещества, которые нельзя представить как спонтанно нарушеные конфигурации поля. К таким состояниям относят спиновые жидкости, электронный газ в дробном квантовом эффекте Холла.

Сверхтекучесть

В качестве примера спонтанного нарушения симметрии в теории фазовых переходов рассматривается переход жидкого $^{4}He$ в сверхтекучее состояние. Как было сказано ранее, бозе-жидкость можно описать одним комплексным полем $\psi$. В теории сверхтекучей бозе-жидкости, предполагая, что атомы жидкости являются твердыми шариками, которые взаимодействуют только при непосредственных столкновениях ($\delta$ -взаимодействие), а дальнего действия взаимодействия отсутствуют, плотность энергии можно записать в виде

$e(x)={\frac {\hbar ^{2}}{2M}}|\nabla \psi |^{2}+{\frac {g}{2}}|\psi |^{4},$

где $\psi$  — комплексное поле, соответствующее волновой функции атомов жидкости,  $M$  — масса атомов жидкости, $g$  — параметр взаимодействия. Химический потенциал имеет вид $\mu =-\mu _{0}\left({\frac {T}{T_{c}}}-1\right)$. Данное выражение для плотности энергии соответствует лагранжиану в теории Гинзбурга — Ландау без внешнего магнитного поля. Впервые, квантовополевое рассмотрение сверхтекучести провел Питаевский. При температурах выше критической, энергия имеет минимум при $\psi =0$. В то же время при понижении температуры ниже критической, минимум реализуется при $|\psi |=a={\sqrt {\frac {-\mu _{0}({\frac {T}{T_{c}}}-1)}{V}}}$. Основное состояние становится бесконечнократно вырожденным по отношению к фазе $\phi =\arg {\psi }$. Удельная свободная энергия (то есть на единицу объёма) выше критической температуры равна нулю $f(T>T_{C})=0$, Однако ниже критической температуры (безотносительно к значению фазы) $f(T<T_{C})=-f_{0}\left({\frac {T}{T_{c}}}-1\right)^{2}$, где $f_{0}={\frac {\mu _{0}^{2}}{2V}}$. Теплоемкость единицы объёма $c=-T{\frac {\partial ^{2}f}{(\partial T)^{2}}}=\left\{{\begin{array}{c}0,\;T>T_{c};\\{\frac {\mu _{0}^{2}}{V}}{\frac {T}{T_{c}^{2}}},\;T>T_{c}.\end{array}}\right.$ Такое поведение теплоемкости соответствует фазовому переходу второго рода. Раскладывая поля $|\psi (x)|=a+\rho (x)$ и $\phi (x)=\phi _{0}+\gamma (x)$ в окрестности вакуума получим

$\epsilon =\int d^{3}x\left[{\frac {1}{2}}\left((\nabla \rho (x))^{2}+(-2m^{2})\rho (x)^{2}\right)+{\frac {1}{2}}a^{2}(\nabla \gamma (x))^{2}\right]$,

где безразмерные величины имеют вид $\epsilon ={\frac {E}{\hbar ^{2}/2M}}$, $m^{2}=-\mu {\frac {2M}{h^{2}}}>0$. Отклонение от вакуумных, находящихся в равновесии значений соответствуют полям возбуждений. Как видим существуют две моды колебаний — массивная мода $\rho$ и безмассовая голдстоуновская мода $\gamma$. Моды колебаний характеризуются корреляционной длиной $\xi _{\varphi }={\frac {1}{m_{\varphi }}}$, которая задает экспоненциальный закон затухания возбуждений с расстоянием $e^{-|x|/\xi }$ . Выше критической точки есть две моды с корреляционной длиной $\xi _{\psi }={\frac {1}{m}}={\sqrt {\frac {\hbar ^{2}}{2M\mu _{0}}}}{\frac {1}{\sqrt {{\frac {T}{T_{c}}}-1}}}$ . Ниже критической точки для голдстоуновских безмассовых мод корреляционная длина бесконечная (это означает на самом деле не экспоненциальную, а степенное поведение возбуждений), что соответствует коррелированности фазовых флуктуаций во всей системе (например бозе-конденсат). Для массивной моды в сверхтекучем состоянии имеем температурную зависимость корреляционной длины в окрестности критической точки фазового перехода

$\xi _{\rho }={\frac {1}{\sqrt {2|m^{2}|}}}={\frac {1}{\sqrt {2}}}{\sqrt {\frac {\hbar ^{2}}{2M\mu _{0}}}}{\frac {1}{\sqrt {1-{\frac {T}{T_{c}}}}}}$.

Объединение фундаментальных взаимодействий

Модель Глэшоу — Вайнберга — Салама

Основная статья: Электрослабое взаимодействие

Модель Глэшоу — Вайнберга — Салама описывает объединённое электрослабое взаимодействие с группой калибровочной симметрии $SU(2)_{L}\times U(1)_{Y}$ и четырьмя калибровочными векторными бозонами $B^{0},\;W^{0},\;W^{+},\;W^{-}$, где индекс вверху указывает электрический заряд бозона. При понижении энергии группа $SU(2)_{L}\times U(1)_{Y}$ сводится к группе $U(1)_{\gamma }$ — электродинамике с одним калибровочным бозоном — фотоном. Заметим, что ненарушенная группа $U(1)_{Y}$ является группой поля гиперзаряда, а не электромагнитного поля. Также в теории появляется скалярное поле, которое превращается по фундаментальному представлению группы $SU(2)$, поэтому оно имеет вид двухкомпонентного комплексного скаляра $\varphi =||\varphi _{1},\varphi _{2}||^{T}$. Кроме того, в модели есть материальные поля, которые мы для простоты считать не будем. Лагранжиан калибровочных полей (точнее бозонного сектора) имеет вид

${\mathcal {L}}=-{\frac {1}{4}}(F_{Y}^{\mu \nu })^{2}-{\frac {1}{4}}(F_{L}^{a,\mu \nu })^{2}+{\mathcal {D}}^{\mu }\varphi ^{\dagger }{\mathcal {D}}_{\mu }\varphi -\lambda \left(\varphi ^{\dagger }\varphi -a^{2}\right)^{2},$

где ковариантная производная от $\varphi$ записывается

${\mathcal {D}}^{\mu }\varphi =\partial ^{\mu }\varphi +{\frac {i}{2}}e_{Y}Z_{U(1)}^{\mu }\varphi +ie_{L}W_{SU(2)}^{a,\mu }{\frac {\sigma _{a}}{2}}\varphi ,$

где $e_{Y}$ и $e_{L}$ — константы взаимодействия соответствующих полей, $\sigma _{a}$ — совокупность единичной матрицы и матриц Паули $\sigma _{i}$. Вакуумное состояние выберем в виде $\varphi _{0}=||0,a||^{T}$. Очевидно, что вакуум является инвариантным относительно действия элементов малой группы $U(1)_{\gamma }$, генератором которой является матрица $t_{A}=\left({\begin{array}{cc}1&0\\0&0\end{array}}\right)$. Именно эта группа отвечает калибровочным преобразованием электродинамики. Удобно ввести тройку матриц $t_{i}=\sigma _{i}/2$, а также переписать параметры $e_{Y}$ и $e_{L}$ через новые параметры $e$ и ${\mathcal {\theta }}_{W}$

$e=e_{Y}\cos {\mathcal {\theta }}_{W}=e_{L}\sin {\mathcal {\theta }}_{W},$

параметр $e$ оказывается равным элементарному электрическому заряду, а параметр ${\mathcal {\theta }}_{W}$ называется углом Вайнберга. В таком случае ковариантная производная запишется

${\mathcal {D}}^{\mu }\varphi =\partial ^{\mu }\varphi +ie\left(A^{\mu }-{\rm {tg}}{\mathcal {\theta }}_{W}Z^{\mu }\right)t_{A}\varphi +i\left({\frac {e_{2}}{\cos {\mathcal {\theta }}_{W}}}Z^{\mu }t_{3}+e_{2}W_{+}^{\mu }t_{1}+e_{2}W_{-}^{\mu }t_{2}\right)\varphi ,$

где ${\begin{pmatrix}A_{\mu }\\Z_{\mu }\end{pmatrix}}={\begin{pmatrix}\cos \theta _{W}&\sin \theta _{W}\\-\sin \theta _{W}&\cos \theta _{W}\end{pmatrix}}{\begin{pmatrix}B_{\mu }\\W_{\mu }^{3}\end{pmatrix}}$, $W_{\mu }^{+}=W_{\mu }^{1}$, $W_{\mu }^{-}=W_{\mu }^{2}$.

В унитарной калибровке $\varphi =||0,a+\phi ||^{T}$, где $\phi$ является действительным скалярным полем, соответствует бозону Хиггса, обнаруженным экспериментально в 2012 году. В квадратичном приближении лагранжиан с нарушенной симметрией запишется в виде

${\mathcal {L}}=-{\frac {1}{4}}(\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu })^{2}-{\frac {1}{4}}(\partial _{\mu }Z_{\nu }-\partial _{\nu }Z_{\mu })^{2}+m_{Z}^{2}Z^{2}-\sum _{i=\pm }\left[{\frac {1}{4}}(\partial _{\mu }W_{\nu }^{i}-\partial _{\nu }W_{\mu }^{i})^{2}+m_{W}^{2}(W^{i})^{2}\right]+(\partial _{\mu }\phi )^{2}-m_{\phi }^{2}\phi ^{2},$

где $m_{W}={\frac {e_{2}a}{\sqrt {2}}}$, $m_{Z}={\frac {e_{2}a}{{\sqrt {2}}\cos {\mathcal {\theta }}_{W}}}$, $m_{\phi }=2{\sqrt {\lambda }}a$.

Следует добавить, что квантовые поправки приводят к изменению масс бозонов и зависимости констант взаимодействия от энергии.

SU(5)-модель Великого Объединения Джорджи — Глэшоу

Основная статья: Теории Великого объединения

Группировка фермионов из 5 + 10 мультиплетов в теории $SU(5)$. Бозоны взаимодействия размещены на пересечении соответствующих фермионных строк и столбцов. Нейтральные бозоны (фотон, Z-бозон) не показаны на рисунке.

При высоких энергиях (~10¹⁴ ГэВ) электрослабое и сильное ядерное взаимодействия объединяются в единое поле с некоторой калибровочной группой симметрии, которая спонтанно нарушается к группе $SU(3)_{C}\times SU(2)_{L}\times U(1)_{Y}$ Стандартной модели при более низких энергиях. В данном параграфе рассмотрим модель Джорджи - Глэшоу с наименьшей калибровочной группой $SU(5)$, которая позволяет Великое объединение.

В этой теории все фермионы объединяются в три поколения 15-компонентных мультиплетов, состоящих из 5-ти и 10-ти компонентных мультиплетов, что соответствуют наименьшим размерностям неприводимых представлений группы $SU(5)$. В 5-компонентный сектор 15-ти компонентного мультиплета входят правый цветной триплет кварков $d$ -типа (по одной компоненте для каждого цвета) и левый лептонный изоспиновый дублет (электрон и нейтрино) $5=||d_{R};e_{L}^{-},\nu _{L}||$. 10-компонентный сектор содержит левый и правый триплеты $u$ -кварков, левый триплет $d$ -кварков и правый электрон $10=||u;d_{L};e_{R}^{-}||$.

При точной симметрии группа $SU(5)$ имеет $5\times 5-1=24$ безмассовых калибровочных бозонов. Существуют три бозоны $W^{+},Z^{0},W^{-}$, отвечающих за переходы в лептонного квинтете и связанные группой $SU(2)_{L}\subset SU(5)$. Также есть бозон $B^{0}$, что соответствует группе $U(1)_{Y}$. Как и в Стандартной модели, фотон и $Z^{0}$ бозон являются ортогональными суперпозициями полей $W^{0}$ и $B^{0}$. Также есть 8 глюонов, осуществляющих переходы между тремя цветными кварками и являющимися генераторами группы $SU(3)_{C}$. Другими двенадцатью калибровочными бозонами являются четыре цветных триплетов $X_{\pm 4/3}$ и $Y_{\pm 4/3}$. Бозоны $X$ и $Y$ отвечают за взаимодействия $\nu _{e}-d_{R}$, $e_{R}^{-}-u_{L}$, $d_{L}-u_{R}$ и $e_{L}-d_{R}$, $e_{R}-d_{L}$, $u_{L}-u_{R}$ соответственно.

При уменьшении энергии симметрия $SU(5)$ нарушается до $SU(3)_{C}\times SU(2)_{L}\times U(1)_{Y}$. При этом калибровочные $X$ — и $Y$ -бозоны приобретают массы 10¹⁴ ГэВ.

Кроме того, в модели $SU(5)$ возможно ввести массивные правые нейтрино (как синглет $SU(5)$). Такое нейтрино может взаимодействовать с квинтетом с помощью бозонов Хиггса, которые возникают при спонтанном нарушении симметрии Великого объединения.

Модель Джорджи — Глэшоу предусматривает время жизни протона ~ 10²⁹ лет, однако современные эксперименты на Super-Kamiokande дают нижнюю оценку для жизни протона 10³² лет, полностью исключая возможность реализации симметрии $SU(5)$ в такой простой версии.

SO(10)-модель и модели с высшими калибровочными группами

Следующей минимальной калибровочной группой, которой можно описать Великое объединение, является группа $SO(10)$, в которой фермионы образуют 16-плет, где по сравнению с $SU(5)$ добавляется левое нейтрино. Можно показать, что всего есть $10\times 9/2=45$ калибровочных бозонов, которые могут приобретать массу при спонтанном нарушении симметрии $SO(10)$. Такая модель тоже исключается отсутствием распада протона.

Впрочем рассматриваются и высшие группы $SU(n)$ и $SO(n)$ (например $SU(8)$, $SO(16)$ и тому подобное), а также модели, где калибровочная группа является произведением двух и более простых групп $SU(4)\times SU(4)$, $SU(3)\times SU(3)\times SU(3)$ и тому подобное. Особое внимание уделяется цепочке исключительных групп

$E_{4}=SU(5)\subset E_{5}=SO(10)\subset E_{6}\subset E_{7}\subset E_{8},$

которые возникают в теориях многомерной гравитации и теории струн. Группы $E_{7},E_{8}$ являются достаточно большими для размещения различных поколений частиц.

Несмотря на большое количество полей в высоких группах, механизм спонтанного нарушения симметрии в соответствующих теориях такой же, как и описано выше.

Спонтанное нарушение суперсимметрии

Основная статья: Суперсимметрия

Спонтанное нарушение суперсимметрии (в отличие от мягкого и динамического) заключается в получении несуперсимметричной (явно) теории в окрестности вакуума с суперсимметрией. Нарушение суперсимметрии является необходимым процессом для избежания конфликта суперсимметричных моделей с экспериментом. Дело в том, что точная суперсимметрия предполагает, что суперпартнеры (количество которых совпадает с количеством обычных частиц) имеют такую же массу, как и их партнеры (обычные частицы), чего не наблюдается в эксперименте. Во время нарушения суперсимметрии, суперпартнеры приобретают значительную дополнительную массу, и, таким образом, становятся пока недостижимыми в экспериментах.

Как и для возбуждения калибровочной симметрии, можно показать, что квантовые поправки не нарушают суперсимметрии, если она не нарушена на классическом уровне. Однако существенным отличием нарушения суперсимметрии от калибровочной симметрии является утверждение следующей теоремы

Теорема. В любой теории с суперсимметрией или нарушены все суперсимметрии, или не нарушена ни одна из них .

Критерии нарушения суперсимметрии

Ненулевые вакуумные средние

Суперсимметрия нарушается тогда и только тогда, когда суперзаряды $Q_{a}$ не уничтожают вакуумное состояние $Q_{a}|0\rangle \neq 0$. Для вакуумного среднего вариации поля $\varphi$ можно написать $\langle \delta \varphi \rangle _{0}=\langle \left[\varphi ,Q_{\alpha }\right]\rangle _{0}\neq 0$. Другими словами суперсимметрия нарушена тогда и только тогда, когда вакуумное среднее некоторого поля равно 0. При этом требуется Лоренц-инвариантность вакуума.

Например, для модели Весса — Цумино

$S=\int d^{4}x\left(-{\frac {1}{2}}(\partial _{\mu }A)^{2}-{\frac {1}{2}}(\partial _{\mu }B)^{2}-{\frac {1}{2}}\chi ^{\dagger }\gamma ^{\mu }\partial _{\mu }\chi +{\frac {1}{2}}D^{2}+{\frac {1}{2}}F^{2}\right)$

с бозоннымы полями $A,B,D,F$ и майоранивским фермионом $\chi$ . поля $D,F$ являются дополнительными и зануляются на массовой поверхности, — их наличие является необходимым для равенства бозонных и фермионных степеней свободы на и вне массовой поверхности. Для этой модели с требования Лоренц-инвариантности вакуума следует $\langle \chi _{\alpha }\rangle =0$, $\langle \partial _{\mu }A\rangle =0$, $\langle \partial _{\mu }B\rangle =0$. Ненулевое среднее вариации поля имеет вид $\langle \delta _{\varepsilon }\chi _{\alpha }\rangle =((\langle F\rangle +i\gamma _{5}\langle D\rangle )\varepsilon )_{\alpha }$. Таким образом суперсимметрия нарушена тогда и только тогда, когда вакуумные средние дополнительных полей не равны 0.

Нулевое значение потенциала

Гамильтониан суперсимметричной теории с суперзарядами $Q_{a}$ записывается в виде

$H=\sum _{a}(Q_{a}Q_{a}^{\dagger }+Q_{a}^{\dagger }Q_{a})$

А это в свою очередь приводит к следующему утверждению: суперсимметричное вакуумное состояние должно иметь нулевую энергию, если вакуумная энергия положительная — суперсимметрия нарушена. Действительно, для вакуумного среднего гамильтониана

Потенциалы с нарушенной симметрией: a) ненарушена калибровочная симметрия и ненарушена суперсимметрия; b) ненарушена калибровочная симметрия и нарушена суперсимметрия; c) нарушена калибровочная симметрия и ненарушена суперсимметрия; d) нарушена калибровочная симметрия и нарушена суперсимметрия.

$\langle H\rangle =\sum _{a}(||Q_{a}|0\rangle ||^{2}+||Q_{a}^{\dagger }|0\rangle ||^{2})\geq 0.$

Здесь равенство достигается только только в случае ненарушенной суперсимметрии $Q_{a}|0\rangle =0$.

В этом заключается принципиальное отличие спонтанного нарушения суперсимметрии от калибровочной симметрии. Для последней важна инвариантность минимума потенциала, а для суперсимметрии — значение его минимума. Таким образом нарушения калибровочной симметрии является в определённом смысле независимым от нарушения суперсимметрии. Если минимум нарушенной относительно калибровочной симметрии вакуума имеет нулевую энергию, то суперсимметрия не является нарушенной.

Голдстино и хиггсино

При нарушении суперсимметрии кирального суперполя $\Phi (x,\theta ,{\overline {\theta }})=\varphi (y)+\theta \chi (y)+\theta \theta F(y),$ где $y=x-i\theta \sigma ^{\mu }{\overline {\theta }}$, $\theta ,\;{\overline {\theta }}$  — грасмановы координаты суперпространства, реализуется так называемое нарушение суперсимметрии $F$ -типа, когда вакуумное среднее динамического скалярного и дополнительного поля $\langle F\rangle _{0}\neq 0$. При нарушении суперсимметрии векторного суперполя $\langle D\rangle _{0}\neq 0$, а о соответствующем нарушении суперсимметрии говорят как о $D$ -типе.

В обоих типах нарушения суперсимметрии существует спинор, который под действием суперсимметричных преобразований получает неоднородной член

$\delta _{\varepsilon }\lambda _{\alpha }=-2\varepsilon _{\alpha }\langle D\rangle +o(\varepsilon ),\qquad \delta _{\varepsilon }\chi _{\alpha }=-2\varepsilon _{\alpha }\langle F\rangle +o(\varepsilon ).$

Такой спинор называют фермионом Голдстоуна или голдстино.

По аналогии с механизмом Хиггса, где векторный бозон «съедает» голдстоуновский бозон и становится массивным, в супергравитации гравитино съедает голдстино (векторный супермультиплет съедает кирально) и становится массивным. Такой механизм называется суперхиггсовским механизмом.

Модель О’Рейферти

Рассмотрим нарушения суперсимметрии на примере модели О’Рейферти с $n$ киральными супермультиплетами $\Phi _{i}$, которая задается лагранжианом

$\int d^{2}\theta d^{2}{\overline {\theta }}\sum _{i}{\overline {\Phi }}_{i}\Phi ^{i}+\int d^{2}\theta W(\Phi )+h.c,$

где черта над полем означает дираковским (или комплексным) сопряжением, $h.c$ обозначает эрмитово-сопряженное слагаемое, а суперпотенциал

$W(\Phi )=a_{i}\Phi ^{i}+{\frac {1}{2}}m_{ij}\Phi ^{i}\Phi ^{j}+{\frac {1}{3}}\lambda _{ijk}\Phi ^{i}\Phi ^{j}\Phi ^{k}$ .

Теперь, варьируя действие, получаем уравнение для дополнительного поля ${\overline {F}}_{i}=-{\frac {\partial W}{\partial \varphi ^{i}}}=-(a_{i}+m_{ij}\varphi ^{j}+\lambda _{ijk}\varphi ^{j}\varphi ^{k})$. Подставляя полученное решение, получим потенциальную энергию

$V=\sum _{i}{\overline {F}}_{i}F^{i}=\sum _{i}\left|-{\frac {\partial W}{\partial \varphi ^{i}}}\right|^{2}=\sum _{i}|a_{i}+m_{ij}\varphi ^{j}+\lambda _{ijk}\varphi ^{j}\varphi ^{k}|^{2}.$

Cуперсиметрия в данной модели нарушена если невозможно найти такой набор $\langle \varphi _{i}\rangle$, чтобы $\langle F^{i}\rangle =0$ для всех компонент.

Неинвариантные вакуумы

При рассмотрении нарушения симметрии квантового поля мы предполагали, что вакуумная конфигурация поля инвариантна относительно преобразований неоднородной группы Лоренца (повороты, бусты и трансляции). Это очень сильное неаргументированное ограничения на вакуумные конфигурации, которое ведет к тому, что вакуум поля одинаков во всех точках пространства. Однако оказывается, что действительно возможны поля с нетривиальныеми координатно-зависимыеми конфигурацииями вакуума. Более того, такие конфигурации могут быть важны при исчислении образующего функционала, поскольку их влияние не является малой величиной (например инстантонный вклад в квантовой хромодинамике. Такими нетривиальными вакуумами являются также магнитные монополи, космические струны и доменные стенки, которые в принципе могут присутствовать во Вселенной и трактоваться как топологические дефекты пространства-времени с ненарушенной калибровочной электрослабой симметрией или симметрией Великого объединения. Такие неинвариантные вакуумные состояния реализуют экстремум функционала действия и являются устойчивыми при возбуждении.

Такие конфигурации хорошо известны в физике конденсированного состояния. Например, доменные стенки между областями Вселенной с различными нарушениями симметрии являются аналогом доменных стенок в ферромагнетиках (откуда и происходит их название), космические струны схожи с вихревыми линиями в сверхпроводнике.

Некоторые типы с неинвариантным вакуумом, которые рассматриваются теоретиками, приведены ниже

Механическая модель Унру

Простая механическая модель предложена Унру. Рассмотрим совокупность карандашей, которые поставлены торцами на стол, а острые концы, которых соединены между собой резинками. Такая система находится в состоянии неустойчивого равновесия   — любое возмущение приведет к падению карандашей и переходу из нестабильного состояния в стабильное вакуумное состояние. Однако направление падения случайно. Картина равновесного состояния имеет много различных вариантов. Конечно, возможно падение карандашей в одном направлении. Однако, может случиться и так, что вокруг некоторого карандаша все остальные карандаши упали в противоположных направлениях. Тогда на центральный карандаш со всех сторон изотропно действуют одинаковые силы натяжения резинок от карандашей, которые уже упали. Поскольку сила натяжения действует равномерно,-по прежнему нестабильное вакуумное состояние в выбранной точке становится стабильным и карандаш не падает. Возникает точка, которая является отличной от остальных точек, где симметрия не является нарушенной.

Конфигурации вакуума с локально ненарушенной калибровочной симметрией

Аналогично как и для механической модели, при нарушении калибровочной симметрии возможны устойчивые состояния с точечно ненарушенной симметрией. Такие решения называются монополями Полякова -т’Хофта.

При нарушении симметрии определённых групп $G$ (например $SU(2)$) к группе электромагнитной калибровочной симметрии $U(1)$ поле монополя Полякова -т’Хофта похоже на магнитное поле, поэтому его отождествляют с магнитными монополями. В этом случае можно показать, что монополь обладает магнитным зарядом кратным $g={\frac {\pm 1}{e}}$, где $e$  — элементарный электрический заряд. Возможны также монопольные конфигурации с большим магнитным зарядом, однако они распадаются до монополей с элементарным магнитным зарядом $g$. Конфигурация скалярных и калибровочных полей для монополя Полякова — т’Хофта может быть выбрана в калибровке $A_{a0}=0$ в виде $\varphi _{i}={\textbf {e}}_{i}\langle \varphi \rangle F(r),$$A_{ai}={\frac {\varepsilon _{ail}{\textbf {e}}_{l}}{er}}G(r)$, где ${\textbf {e}}_{i}={\frac {x_{i}}{r}}$, $\varepsilon _{ijk}$  — символ Леви-Чивита, индекс $a$ векторного поля групповым, второй индекс   — координатным, $F(r),\,G(r)$  — некоторые функции, аналитический вид для которых установить не удается.

Поле монополя Полякова — т’Хофта в калибровке $\varphi _{i}=\varphi \delta _{i3}$ для скалярных полей, где $\delta _{ij}$  — дельта-символ Кронекера, имеет вид

$B_{i}={\frac {1}{2}}\varepsilon _{ijk}(\partial _{j}A_{k}^{3}-\partial _{k}A_{j}^{3})=-{\frac {{\textbf {e}}_{i}}{er^{2}}}.$

Количество монополей, которые должны образоваться в результате нарушения симметрии Великого Объединения составляет один монополь на 10³ нуклонов, противоречит наблюдаемым данным. Отсутствие монополей объясняется инфляцией. Считается, что они были образованы перед фазовым переходом поля с симметрией Великого объединения в симметрию Стандартной модели, а сопровождающая этот переход инфляция привела к разжижению газа монополей. Более того, отсутствие магнитных монополей считается одним из аргументов в поддержку инфляционной теории эволюции Вселенной.

Существуют также точечные вакуумные полевые конфигурации дионы, которые обладают как электрическим так и магнитным зарядами.

Возможны также полевые конфигурации с локально ненарушенной калибровочной симметрией больших размерностей   — это одномерные космические струны и доменные стенки.

Инстантоны

Для нелинейных полевых теорий (например квантовой хромодинамики) возможны нетривиальные полевые конфигурации в (1 + 3)-пространстве, которые называют инстантонами. Они являются обобщением солитона на (1 + 3) -мерное пространство. Такие конфигурации реализуют экстремум действия. Они непертурбативны (их невозможно получить в одном порядке теории возмущений).

Тем не менее вклад инстантонов и флуктуаций в окрестности инстантонного состояния в образующий функционал значителен. Инстантоны решают $U(1)$ — проблему нарушения киральной симметрии. В теории электрослабых взаимодействий именно инстантонные конфигурации слабого $SU(2)_{L}$ -поля объясняют нарушение барионного и лептонного чисел. Инстантонные состояния играют важную роль и при распаде фальшивого вакуума (см. ниже).

Скирмионы

Эффективные теории поля с лагранжианом типа линейной сигма-модели хорошо описывают низкоэнергетическое мезонное поведение. Однако для согласованности расчета параметров взаимодействия мезонов при высоких энергиях необходимо лагранжиан дополнять слагаемыми с высшими степенями по полевым производным

${\mathcal {L}}={\mathcal {L}}_{\sigma }(\varphi )+f_{abcd}{\varphi }\partial _{\mu }\varphi ^{a}\partial ^{\mu }\varphi ^{b}\partial _{\nu }\varphi ^{c}\partial ^{\nu }\varphi ^{d}+....$

Наличие высших степеней производных может позволять стойку нетривиальную вакуумную конфигурацию поля, которую называют скирмионами.

Скирмионы также могут возникать и в статистической физике и при динамическом нарушении симметрии.

Диагонализации мгновенного гамильтониана

Для неинвариантных вакуумов четко непонятно, что считать частью и вообще можно говорить о частицах в случае произвольной вакуумной конфигурации. В квантовой теории поля оператор поля ${\widehat {\Phi }}$ представляется как функция операторов рождения и уничтожения $b_{\textbf {k}}^{+},\,b_{\textbf {k}}$, которые удовлетворяют определённым (анти) коммутационным соотношениям, вид которых зависит от лагранжиана и типа (ферми или бозе) поля. Если соответствующий гамильтониан теории диагональный по отношению к этим операторов, то понятие частицы имеет простую интерпретацию. Вакуумное состояние определяется из уравнения $b_{\textbf {k}}|0\rangle =0$ и соответствует состоянию с наименьшим собственным значением гамильтониана, состояния без частиц. Частицей с импульсом ${\textbf {k}}$ считается состояние $|1_{\textbf {k}}\rangle =b_{\textbf {k}}^{+}|0\rangle$.

Однако в случае зависимости гамильтониана (а следовательно вакуумного и возбужденных состояний) от времени оказывается, что состояние, которое интерпретируется частицей в данный момент времени, в последующие моменты времени уже частицей не будет. Тем не менее, можно развить простой формализм в случае нестационарного вакуума — метод диагонализации мгновенного гамильтониана. Согласно этому методу предполагается, что в некоторый момент времени, например $t_{0}=-\infty$, диагонализован гамильтониан и найдены операторы рождения и уничтожения $b_{A}^{+}(t_{0}),\,b_{A}(t_{0})$ здесь индекс $A$ обозначает все квантовые числа поля. Поиск такого вакуума можно осуществить, рассматривая при $t=-\infty$ невзаимодействующие поля и адиабатически включая взаимодействие (параметры взаимодействия) с помощью множителя $\lim _{\lambda \rightarrow +0}e^{\lambda t}$.

Операторы рождения и уничтожения во все последующие моменты времени получаем с помощью преобразований Боголюбова

$b_{A}(t)=u_{A}^{B}(t)b_{B}(t_{0})+v_{A}^{B}(t)b_{B}^{+}(t_{0})$

и преобразований, полученных из данного сопряжением (эрмитовым или комплексным). Функции $u(t),\,v(t)$ определяются из условия выполнения соответствующих коммутационных соотношений и диагонализации гамильтониана в данный момент времени $t$ . В данном формализме через неэквивалентность вакуума в разные моменты времени будет наблюдаться рождения и уничтожения частиц в ходе эволюции (аналог эффекта Унру). Количество частиц, которые родятся в момент времени $t$ равна

$N_{0}(t)=\sum _{A}\langle t_{0}|a_{A}^{+}(t)a_{A}(t)|t_{0}\rangle .$

Такая корпускулярная интерпретация неинвариантных вакуумов не является единственно возможной.

Гравитация как хиггс-голдстоунивское поле

Впервые на возможность трактовки гравитона как голдстоуна^{[уточнить]} указали Гайзенберг и Иваненко. Позже такая идея развивалась с разных точек зрения. В данном разделе представлено краткое введение в проблему.

Калибровочная гравитация

Согласно современным воззрениям, поля фундаментальных взаимодействий возникают из необходимости инвариантности функции Лагранжа поля материи относительно локальных калибровочных преобразований. Как было показано ранее, для включения взаимодействия между полем материи и калибровочным полем обычную производную от поля заменяют на ковариантную производную. Кроме того, калибровочное поле под действием калибровочных преобразований изменяется определённым образом. Калибровочные преобразования образуют компактную группу Ли.

С геометрической точки зрения калибровочные поля представляют собой связности в расслоенном пространстве в случае внутренних калибровочных симметрий — в пространстве с локально тривиальным расслоением. Расслоенное пространство обобщает понятие касательного расслоения, заменяя касательное пространство в каждой точке многообразия на произвольное векторное пространство (например комплексное пространство в случае заряженного поля Клейна — Гордона или пространство лептонной пары ($e,\,\nu _{e}$). Таким образом геометрия теории калибровочных полей очень схожа с теорией относительности.

С другой стороны, гравитационное поле следует рассматривать как калибровочное поле с определённой группой симметрии. Однако оказывается, что для гравитационного поля существуют две калибровочные симметрии. Первая задается общими ковариантными преобразованиями тензорных величин

${T'}_{\nu _{1}...\nu _{n}}^{\mu _{1}...\mu _{m}}={\frac {\partial x'^{\mu _{1}}}{\partial x^{\alpha _{1}}}}\cdot ...\cdot {\frac {\partial x'^{\mu _{m}}}{\partial x^{\alpha _{m}}}}{\frac {\partial x^{\beta _{1}}}{\partial x'^{\nu _{1}}}}\cdot ...\cdot {\frac {\partial x^{\beta _{n}}}{\partial x'^{\nu _{n}}}}T_{\beta _{1}...\beta _{n}}^{\alpha _{1}...\alpha _{m}},$

которые составляют математическое отражение общего принципа относительности Эйнштейна. Эти преобразования образуют группу $GL(4,R)$.

Однако сам принцип относительности не фиксирует никак (1 + 3) -мерную псевдоевклидовую структуру пространства-времени. Кроме того, обще-ковариантные преобразования не учитывают другую симметрию в общей теории относительности, а именно симметрию относительно поворотов, бустов и трансляций в локальных системах отсчета (касающихся пространственно-временного многообразия пространствах). Для учёта этих фактов в теорию вводится метрический тензор $g^{\mu \nu }$. Удобно метрический тензор представлять в тетрадном форме $g^{\mu \nu }=\eta ^{ab}e_{a}^{\mu }e_{b}^{\nu }$, где латинские индексы отражают локальные лоренцевские индексы, тетрады $e_{a}^{\mu }$ задают переход между обще-ковариантными и локальными лоренцевскими индексами, $\eta ^{ab}$$\eta ^{ab}={\rm {diag}}{(1,-1,-1,-1)}$  — тензор Минковского.

Поле калибровочной обще-ковариантной симметрии можно легко отождествить со связностью гравитационного поля (символами Кристоффеля) $\Gamma _{\mu \beta }^{\alpha }$. Действительно, выражения для ковариантной производной и калибровочных преобразований связности напоминают аналогичные выражения для поля Янга — Миллса

$\nabla _{\mu }A_{\beta }=\partial _{\mu }A_{\beta }-\Gamma _{\mu \beta }^{\alpha }A_{\alpha },$

${\Gamma '}_{\mu \beta }^{\alpha }={\frac {\partial x'^{\alpha }}{\partial x^{\gamma }}}\left(\Gamma _{\nu \sigma }^{\gamma }{\frac {\partial x^{\nu }}{\partial x'^{\mu }}}\right){\frac {\partial x^{\sigma }}{\partial x'^{\beta }}}+{\frac {\partial x'^{\alpha }}{\partial x^{\gamma }}}\partial '_{\mu }{\frac {\partial x^{\gamma }}{\partial x'^{\beta }}}.$

В то же время аналогичного выражения для метрического тензора (тетрадного поля) нет и его калибровочный статус остается неясным.

Метрика как хиггс-голдстоуновское поле

Такая идея в большой степени развивалась Иваненко и Сарданашвили. В данном параграфе изложим основную её суть.

При отсутствии гравитационного поля многообразие пространства-времени, а также действие материальных полей являются инвариантными относительно преобразований неоднородной группы Лоренца. Однако при включении гравитации, лоренцевская инвариантность системы нарушается. Имеет место нарушение симметрии, где хиггс-голдстоуновское поле ассоциируется с метрикой $g^{\mu \nu }$.

Тем не менее, как и в случае нарушения внутренних калибровочных симметрий, в метрике можно выделить Лоренц-инвариантную хиггсовскою составляющую   — тензор Минковского $\eta ^{\mu \nu }$. Отклонение от метрики Минковского $h_{\mu \nu }=g_{\mu \nu }-\eta _{\mu \nu }$ (или равноценно тетрады $e_{a}^{\mu }$) играют роль голдстоуновских составляющих. Однако в отличие от картины нарушения симметрии поля Янга — Миллса, голдстоуновские гравитационные поля могут зануляться в каждой точке пространства-времени каким-либо выбором калибровки (как было сказано унитарная калибровка зануляет голдстоуновские моды только для компактных калибровочных групп Ли). Геометрическая причина этого заключается в том, что локальные преобразования в касательных пространствах действуют на производные $\partial _{\mu }$ как на векторы только в плоском пространстве, для которого касательное пространство совпадает с ним самим. В криволинейном пространстве векторами относительно локальных преобразований являются величины $e_{a}^{\mu }\partial _{\mu }$. Таким образом попытка описать всё криволинейное пространство-время исключительно хиггсовской метрикой Минковского приводит лишь к переходу в тетрадный формализм.

Гравитация как эффект поляризации вакуума

Намеком на трактовку гравитационного поля в похожей манере с бозоном Хиггса является возможность получения лагранжиана гравитационного поля с учёта поляризации вакуума как было получено из эффективного лагранжиана для поля Хиггса выше. Рассмотрим систему полей $\varphi$ в криволинейном пространстве, если это скалярные невзаимодействующие поля, то соответствующее действие имеет вид

$S_{m}=\int d^{4}x{\sqrt {-g}}\left({\frac {1}{2}}\partial ^{\mu }\varphi \partial _{\mu }\varphi -{\frac {1}{2}}m^{2}\varphi ^{2}+\xi R\varphi ^{2}\right),$

где ${\sqrt {-g}}$  — определитель метрического тензора, $R$  — скалярная кривизна, $\xi$  — некоторая константа, которую из требования конформной инвариантности полагают равной $\xi =1/6$. Если внести определённое затравочное слагаемое и добавить интегрирование по полю метрики $g$, а затем проинтегрировать по скалярным полям, то можно получить эффективное действие $S_{eff}$ из которой выделить независимый от $\varphi$ лагранжиан вида

${\mathcal {L}}_{gr}={\sqrt {-g}}\left[-A+BR+CR_{\alpha \beta \mu \nu }R^{\alpha \beta \mu \nu }+DR_{\mu \nu }R^{\mu \nu }+E\partial ^{2}R+FR+GC_{\alpha \beta \mu \nu }C^{\alpha \beta \mu \nu }\right],$

где $A,\,B,\,C,\,D,\,E,\,F,\,G$  — некоторые константы, значения которых зависит от типа $\varphi$, $R_{\alpha \beta \mu \nu }$  — тензор кривизны Римана, $R_{\mu \nu }$  — тензор Риччи, $C_{\alpha \beta \mu \nu }$  — тензор Вейля. В случае скалярных полей $C={\frac {a}{180}}$, $D=-{\frac {a}{180}}$, $E={\frac {a}{5}}\left(\xi -{\frac {1}{6}}\right)$, $F={\frac {a}{2}}\left(\xi -{\frac {1}{6}}\right)^{2}$, $G=0$, константа $a$ выражается через спин поля, константы $A,\,B$ неограничены при снятии регуляризации константы, однако можно перенормировать и выразить через космологическую постоянную и гравитационную постоянную.

Интересно также, что при некотором наборе констант $A,\,B,\,C,\,D,\,E,\,F,\,G$ свободное гравитационное поле ($R_{\mu \nu }=0$) можно проквантовать, а соответствующая теория является перенормируемой.

Нарушение фальшивого вакуума

Часто потенциальная энергия (эффективный потенциал в квантовом случае) имеет не один минимум, а несколько. Различным вакуумам отвечают разные энергии. Вакуум с наименьшей энергией называют истинным, а все остальные   — ложными (фальшивыми). Если после нарушения симметрии и образования дополнительных вакуумов, состояние системы, которое было настоящим вакуумом, стало ложным, система не перейдет сразу в истинный вакуум (например двухъямный потенциал с небольшой ямкой в точке $\varphi =0$, в которой находится система). Если яма неглубокая, то достаточно интенсивные внешние флуктуации могут перевести систему в соседней вакуум с меньшей энергией. Если же потенциальная яма достаточно глубокая, то переход системы из метастабильного ложного вакуума в истинный происходит благодаря квантовому туннелированию.

Динамика распада выглядит следующим пузырьковым образом. В определённой точке пространства образуется истинный вакуум приводит к образованию такого же истинного вакуума во всех соседних точках   — пузырь начинает расти со скоростью света, пока не встретит фронт расширения другого пузыря. Плотность энергии сосредоточена в основном на границе пузырьков, а внутри пузырь пустой.

Математически при исчислении амплитуды перехода выбирается такой контур интегрирования, чтобы можно было учесть имеющуюся инстантонную конфигурацию $\varphi _{inst}$, которая дает для амплитуды перехода преимущественное экспоненциальный множитель $\exp {(-S[\varphi _{inst}])}$, где $S[\varphi _{inst}]>0$  — значение действия для инстантона.

Инфляция как распад ложного вакуума

Схематическое изображение фальшивого SU(5) вакуума и истинного SU(3) х SU(2) x U(1) вакуума перед началом инфляции.

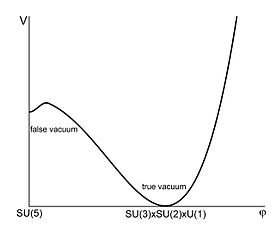
Десятки факторов указывают на наличие в ранний этап эволюции Вселенной фазы экспоненциального расширения — инфляции. С другой стороны, из космологической модели Фридмана следует, что ускорение $a$, которое получает тело под действием гравитации материи равно

$a=-{\frac {4}{3}}\pi G(\varepsilon +3P)R,$

где $G$  — гравитационная постоянная, $\varepsilon ,\,P$  — плотность энергии и давление материи во Вселенной, $R$  — радиус сферы, внутри которой содержится материя (Вселенной). Имея уравнения состояния материи, которое связывает давление и плотность, можем вычислить ускорение. Для всех полей материи давление и энергия положительные величины, поэтому $a<0$ и Вселенная сжимается.

Для физического вакуума, в котором происходят непрерывные процессы рождения и аннигиляции виртуальных пар частица-античастица давление является отрицательным и соответствует по модулю плотности энергии $P_{vac}=-\varepsilon _{vac}$. В таком случае, при отсутствии полей материи

$a={\frac {8\pi G\varepsilon _{vac}}{3}}R={\frac {\Lambda }{3}}R.$

Тогда, можно показать, что $R(t)=R_{0}\exp {({\sqrt {\Lambda /3}}t)}$, то есть Вселенная расширяется экспоненциально (расширение де-Ситтера).

Однако при охлаждении горячей Вселенной в пред-инфляционный период Вселенная была наполнена квантами полей Великого объединения (например поля $SU(5)$) с плотностью $\varepsilon _{vac}/c^{2}\approx 10^{74}$ г/см^3, то есть вовсе не была пустой. Но Вселенная достаточно остыла для того, чтобы этот вакуум уже был ложным (см. Рис) и в нём начали образовываться пузырьки истинного вакуума размером ~ 10⁻²⁰ см, радиус которых увеличивался со скоростью света. Поскольку внутри пузырь пустой, то её размеры сопровождались показательному де-Ситтеровским расширением. На конец инфляции размеры пузырьки составляли 10³² — 10⁴⁰ см (размеры видимой сейчас Вселенной 10²⁸ см, то есть мы полностью живем в одной такой пузырьке).

Нобелевские премии за исследования спонтанного нарушения симметрии

Основная статья: Список лауреатов Нобелевской премии по физике

В данном разделе приведён список лауреатов Нобелевской премии, исследования которых мало связь или прямо касается (2008, 2013) спонтанного нарушения симметрии.

• 1979 — Шелдон Ли Глэшоу, Вайнберг и Абдус Салам — «за вклад в объединенную теорию слабых и электромагнитных взаимодействий между элементарными частицами, в том числе предсказания слабых нейтральных токов».
• 1982 — Кеннет Вильсон — «за теорию критических явлений в связи с фазовыми переходами».
• 1999 — Герард тьХоофт и Мартинус Велтман — «за прояснение квантовой структуры электрослабых взаимодействий».
• 2008 — Йоитиро Намбу — «за открытие механизма спонтанного нарушения симметрии на субатомном уровне» и — Макото Кобаяси и Тосихидэ Масукава — «за установление происхождения симметрии, предполагает существование в природе по меньшей мере трех поколений кварков».
• 2013 — Франсуа Энглер и Питер Хиггс — «за теоретическое открытие механизма, который помогает нам понимать происхождение массы субатомных частиц и существование которого было доказано обнаружением предусмотренной элементарной частицы в экспериментах ATLAS и CMS на Большом адронном коллайдере в CERN».

См. также

• Теория устойчивости
• Спонтанное нарушение электрослабой симметрии

Ссылки

• В. П. Шелест. СПОНТАННОЕ НАРУШЕНИЕ СИММЕТРИИ  (рус.). Физическая энциклопедия. Дата обращения: 30 сентября 2019.