Деление (математика)
| Деление | |
|---|---|
 | |
| Обозначение | обелюс |
| Противоположно | умножение |
Деле́ние (операция деления) — действие, обратное умножению. Деление обозначается двоеточием , обелюсом , косой чертой или записывается в виде дроби.
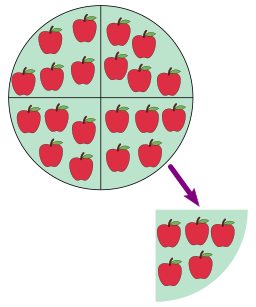
Для натуральных чисел деление обозначает нахождение, какое число (частное) надо взять столько-то (делитель) раз, чтобы получилось данное (делимое).
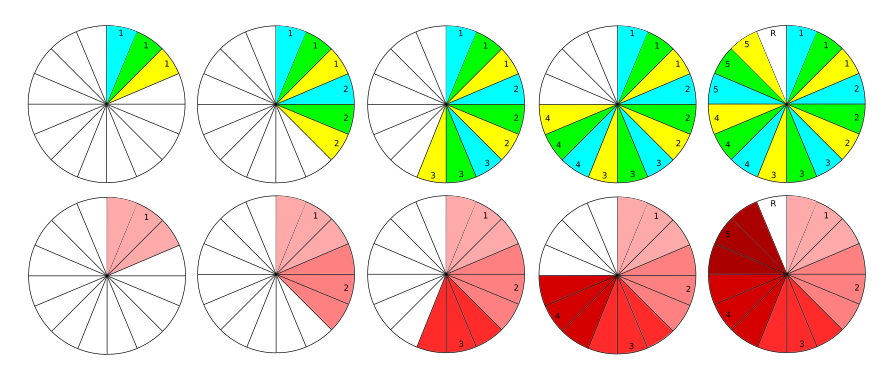
Другими словами, это нахождение максимально возможного количества повторений вычитания делителя из делимого; либо нахождение такой наибольшей величины, которая может быть отнята от делимого столько раз, сколько указано в делителе.
Рассмотрим, например деление на :
Сколько раз содержится в ?
Повторяя операцию вычитания из , мы находим, что содержится в четыре раза, и ещё «остаётся» число .
В этом случае число называется делимым, число — делителем, число — (неполным) частным и число — остатком (от деления).
Полным частным, отношением или соотношением чисел и называется такое число , что . В случае, когда и , их полное частное может быть записано в виде дроби или десятичной дроби .
Полное и неполное частные чисел и совпадают тогда и только тогда, когда делится нацело (делится) на . Соответствующее свойство данной пары чисел называется делимостью.
Формы записи и терминология[править | править код]
Деление записывается с использованием одного из «знаков деления» — «» между аргументами, такая форма записи называется инфиксной нотацией. В данном контексте знак деления является бинарным оператором. Знак деления не имеет специального названия, как например знак сложения, который называется «плюс».
- Самый старый из используемых символов видимо — косая черта (/). Впервые его использовал английский математик Уильям Отред в своём труде «Clavis Mathematicae» 1631 г.
- Немецкий математик Лейбниц предпочитал знак в виде двоеточия (:) Этот символ он использовал в своём труде Acta eruditorum 1684 г. До Лейбница этот знак был использован англичанином Джонсоном в 1633 году в своей книге, но как знак дроби, а не деления в узком смысле.
- Йоханн Ран ввёл знак обелюс (÷) в качестве знака деления, она появилась в его книге «Teutsche Algebra» 1659 г. Знак Рана часто называют «английским знаком деления».
В русскоязычных учебниках математики в основном используется знак в виде двоеточия (:). Косая черта (/) используется в компьютерной нотации. Результат записывается с использованием знака равенства «», например:
- ;
- («шесть разделить на три равно два»);
- («шестьдесят пять разделить на пять равно тринадцать»).
Свойства[править | править код]
Операция деления на числовых множествах имеет следующие основные свойства:
- Деление не перестановочно (не коммутативно) — от перемены мест аргументов частное изменяется:
- Деление не ассоциативно — при последовательном выполнении деления трёх или более чисел последовательность выполнения операций имеет значение, результат изменится:
- Деление дистрибутивно справа, это — свойство согласованности двух бинарных операций, определённых на одном и том же множестве, также известно, как распределительный закон[1] :
- Относительно деления в множестве существует единственный нейтральный элемент справа (число ), деление на единицу (или нейтральный элемент) даёт число, равное исходному:
- Нейтральный элемент справа:
- Относительно деления в множестве существует единственный обратный элемент, получаемый делением единицы на число, что даёт число, обратное исходному:
- Относительно деления в множестве существует единственный нулевой элемент слева — число , делённое на любое число, даёт нуль:
- Нулевой элемент слева:
- По правилам обычной арифметики деление на ноль (нулевой элемент) не определено;
- Деление на противоположный элемент даёт минус единицу:
Результат деления не всегда является определённым для множеств натуральных чисел и целых чисел , чтобы получить натуральное или целое число в результате деления, делимое должно быть кратно делителю. Невозможно в рамках этих чисел получить дробный результат. В этом случае говорится о делении с остатком. То есть деление на этих множествах есть частичная бинарная операция.
Операция деления, определённая на множествах (в полях) рациональных , вещественных и комплексных чисел , даёт число (частное), принадлежащее этому же множеству, следовательно, множества замкнуты относительно операции деления (в точке 0 имеется разрыв второго рода — следовательно кольца рациональных, вещественных и комплексных чисел разомкнуты относительно операции деления).
В математических выражениях операция деления имеет более высокий приоритет по отношению к операциям сложения и вычитания, то есть она выполняется перед ними.
Выполнение деления[править | править код]

Деление является гипероператором вычитания и сводится к последовательному вычитанию. :
где: — последовательность операций вычитания, выполненная раз.
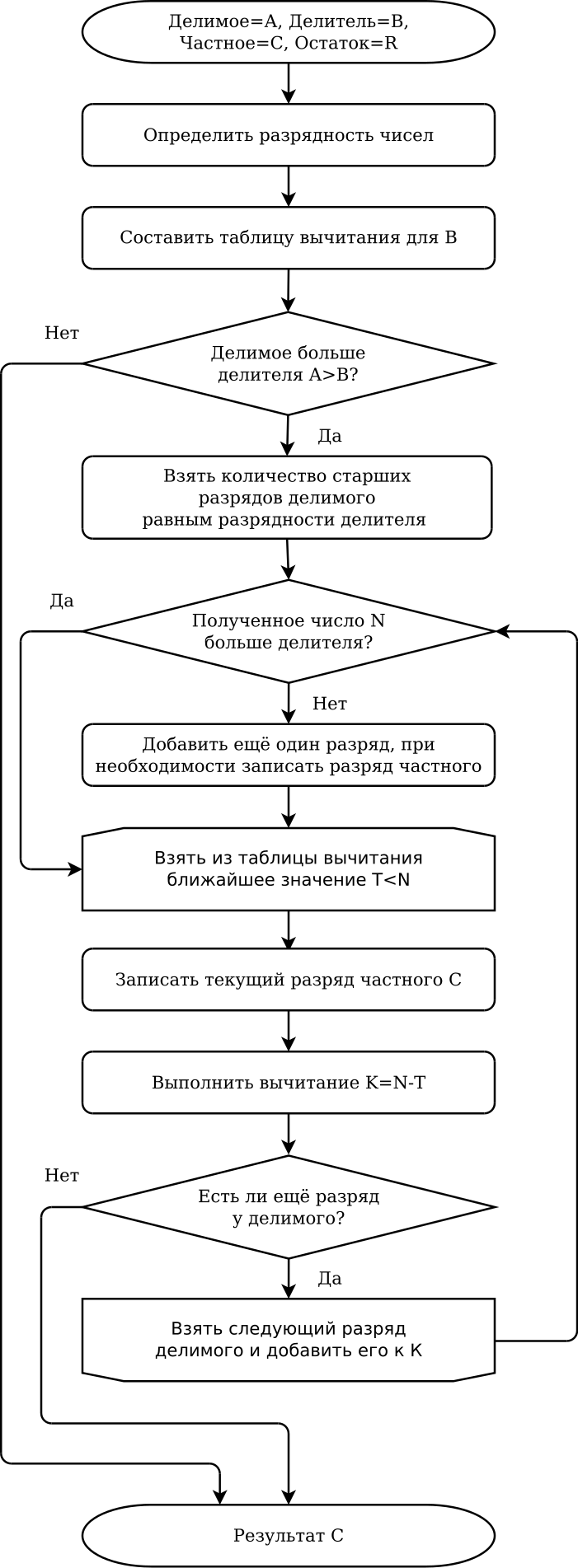
При практическом решении задачи деления двух чисел необходимо свести её к последовательности более простых операций: вычитание, сравнение, перенос и др. Для этого разработаны различные методы деления, например для чисел, дробей, векторов и др. В русскоязычных учебниках математики в настоящее время используется алгоритм деления столбиком. При этом следует рассматривать деление как процедуру (в отличие от операции).
Схема, иллюстрирующую места для записи делимого, делителя, частного, остатка и промежуточных вычислений при делении столбиком:

Из приведенной схемы видно, что искомое частное (или неполное частное при делении с остатком) будет записано ниже делителя под горизонтальной чертой. А промежуточные вычисления будут вестись ниже делимого и нужно заранее позаботиться о наличии места на странице. При этом следует руководствоваться правилом: чем больше разница в количестве знаков в записях делимого и делителя, тем больше потребуется места.
Как видим, процедура достаточно сложная, состоит из относительно большого числа шагов и при делении больших чисел может занять продолжительное время. Данная процедура применима к делению натуральных и целых (с учётом знака) чисел. Для других чисел используются более сложные алгоритмы.
Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и в десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами[2]. При этом нужно пользоваться таблицей вычитания соответствующей данному основанию системы счисления.
Пример деления натуральных чисел в двоичной, десятичной и шестнадцатеричной системах счисления:
110010│101 │ 0 — 0 50800│25 │ 0 — 0 CD530│A8 │ 0 — 0
101 │1010 │ -101 — 1 50 │2032 │ -25 — 1 A8 │138E │ -A8 — 1
10 08 │ -50 — 2 255 │ -150 — 2
0 0 │ -75 — 3 1F8 │ -1F8 — 3
101 80 │ -100 — 4 5D3 │ -2A0 — 4
101 75 │ ... — ... 540 │ -348 — 5
00 50 930 │ -3F0 — 6
0 50 930 │ -498 — 7
0. 0. 0. │ -540 — 8
│ -5E8 — 9
│ -690 — A
│ -738 — B
│ -7E0 — C
│ -888 — D
│ -930 — E
Деление чисел[править | править код]
Натуральные числа[править | править код]
Воспользуемся определением натуральных чисел как классов эквивалентности конечных множеств. Обозначим классы эквивалентности конечных множеств порождённых биекциями, с помощью скобок: . Тогда математическая операция «деление» определяется следующими образами:
- — деление на равные части (отыскание числа элементов в каждом подмножестве разбиения), частным чисел и называется число элементов каждого подмножества разбиения;
- — деление по содержанию (отыскание числа подмножеств разбиения), частным чисел и называется число (количество) подмножеств разбиения;
где: это — разбиение конечного множества на равночисленные попарно не пересекающиеся подмножества, такие что:
для любых коэффициентов , таких что
— остаток (множество оставшихся элементов), ,
— нульарная операция "выделение элемента".
В случае, если одно натуральное число не делится на другое без остатка, говорится о делении с остатком. На остаток накладываются следующее ограничение (чтобы он был корректно, то есть однозначно, определён): , ,
где: — делимое, — делитель, — частное, — остаток.
Данная операция на классах введена корректно, то есть не зависит от выбора элементов классов, и совпадает с индуктивным определением.
Арифметическая операция «деление» частична для множества натуральных чисел , (для полукольца натуральных чисел).
Деление целых чисел[править | править код]
Деление произвольных целых чисел несущественно отличается от деления натуральных чисел — достаточно поделить их модули и учесть правило знаков.
Однако деление целых чисел с остатком определяется неоднозначно. В одном случае, (так же как и без остатка) рассматривают сначала модули и в результате остаток приобретает тот же знак, что делитель или делимое (например, с остатком (-1)); в другом случае понятие остатка напрямую обобщается и ограничения заимствуются из натуральных чисел:
- .
Для устранения неоднозначности принято соглашение: остаток от деления всегда неотрицателен.
Деление рациональных чисел[править | править код]
Замыкание множества целых чисел по операции деления приводит к расширению его до множества рациональных чисел. Это приводит к тому, что результатом деления одного целого числа на другое всегда является рациональное число. Более того, полученные числа (рациональные) уже полностью поддерживают операцию деления (замкнуты относительно неё).
Правило деления обыкновенных дробей:
Деление вещественных чисел[править | править код]
Множество вещественных чисел — непрерывное упорядоченное поле, обозначается . Множество вещественных чисел не является счётным, его мощность называется мощностью континуума. Арифметические операции над вещественными числами представимых бесконечными десятичными дробями определяются как непрерывное продолжение[3] соответствующих операций над рациональными числами.
Если даны два вещественных числа, представимые бесконечными десятичными дробями:
определённые соответственно фундаментальными последовательностями рациональных чисел (удовлетворяющие условию Коши), обозначенные как: и , то их частным называют число , определённое частным последовательностей и :
- ,
вещественное число , удовлетворяет следующему условию:
Таким образом частное двух вещественных чисел и является такое вещественное число которое содержится между всеми частными вида с одной стороны и всеми частными вида с другой стороны[4]. Дедекиндово сечение позволяет однозначно определить результат деления.
На практике для того, чтобы разделить два числа и , необходимо заменить их с требуемой точностью приближёнными рациональными числами и . За приближенное значение частного чисел берут частное указанных рациональных чисел . При этом не важно, с какой стороны (по недостатку или по избытку) взятые рациональные числа приближают и . Деление производится по алгоритму деления столбиком.
Абсолютная погрешность частного приближённых чисел: , абсолютная погрешность числа принимается равной половине последней единицы разряда этого числа.
Относительная погрешность частного равна сумме относительных погрешностей аргументов: . Полученный результат округляют до первой верной значащей цифры, значащая цифра приближенного числа является верной, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.
Пример деления , с точностью до 3-го знака после запятой:
- Округляем данные числа до 4-го знака после запятой (для повышения точности вычислений);
- Получаем: ;
- Делим столбиком: ;
- Округляем до 3-го знака после запятой: .
График[править | править код]
На множестве пар вещественных чисел область значений функции деления графически имеет вид гиперболического параболоида — поверхности второго порядка[5].

Так как , то и для этих множеств область значений функции деления будет принадлежать этой поверхности.
Деление комплексных чисел[править | править код]

Множество комплексных чисел с арифметическими операциями является полем и обычно обозначается символом .
Алгебраической форма[править | править код]
Частным двух комплексных чисел в алгебраической форме записи, называется комплексное число, равное:
где: — комплексные числа, , — мнимая единица; .
На практике частное комплексных чисел находят умножением делимого и делителя на число, комплексно-сопряженное делителю:
делитель становится действительным числом, а в числителе умножаются два комплексных числа, затем полученная дробь почленно делится. Результат определён для всех
Тригонометрическая форма[править | править код]
Для того, чтобы разделить два комплексных числа в тригонометрической форме записи, нужно разделить модуль делимого на модуль делителя, а из аргумента делимого вычесть аргумент делителя:

где: — модуль и аргумент комплексного числа; .
То есть модуль частного двух комплексных чисел равен частному модулей, а аргумент — разности аргументов делимого и делителя.
Показательная (экспоненциальная) форма[править | править код]
Деление комплексного числа в показательной форме, на комплексное число сводится к повороту вектора, соответствующего числу , на угол и изменению его длины на раз. Для частного комплексных чисел в показательной форме верно равенство:
где: — число e; .
Экспоненциальная запись[править | править код]
В экспоненциальной записи числа записываются в виде , где — мантисса, — характеристика числа, — основание системы счисления, . Для деления двух чисел, которые записаны в экспоненциальной форме необходимо разделить мантиссы и характеристики:
Например:
Деление физических величин[править | править код]
Единица измерения физической величины имеет определённое наименование (размерность): для длины (L) — метр (м), для времени (T) — секунда (с), для массы (M) — грамм (г) и так далее. Поэтому, результат измерения той или иной величины представляет собой не просто число, а число с наименованием[6]. Наименование представляет собой самостоятельный объект, который равноправно участвует в операции деления. При производстве операции деления над физическими величинами, делятся как сами числовые составляющие, так и их наименования.
Помимо размерных физических величин существуют безразмерные (количественные) величины, которые формально являются элементами числовой оси, то есть числами, не имеющие привязки к определённым физическим явлениям (измеряются «штуками», «разами» и тому подобное). При делении чисел представляющих собой физические величины на безразмерную величину, делимое число изменяется по величине и сохраняет единицу измерения. Например если взять 15 гвоздей и разложить в 3 коробки, то в результате деления получим 5 гвоздей в каждой коробке:
Деление разнородных физических величин надо рассматривать как нахождение новой физической величины, принципиально отличающейся от величин, которые мы делим. Если физически возможно создание такого частного, например, при нахождении работы, скорости или других величин, то эта величина образует множество, отличное от начальных. В этом случае композиции этих величин присваивается новое обозначение (новый термин), например: плотность, ускорение, мощность и прочее[7].
Например, если разделить длину на время соответствующие одному физическому процессу, то получится именованное число (физическая величина) соответствующее этому же физическому процессу, которая называется «скорость» и измеряется в «метрах в секунду»:
При описании математическими средствами физических процессов немаловажную роль играет понятие однородности, которое означает например, что «1 кг муки» и «1 кг меди» принадлежат разным множествам {мука} и {медь} соответственно и не могут быть непосредственно разделены. Также понятие однородности предполагает, что делимые величины принадлежат одному физическому процессу. Недопустимо делить, например скорость лошади на время собаки.
Деление в алгебре[править | править код]
В отличие от простейших арифметических случаев, на произвольных множествах и структурах деление может быть не только не определено, но и обладать множественностью результата.
Обычно в алгебре деление вводится через понятие единичного и обратного элементов. Если единичный элемент вводится однозначным образом (обычно аксиоматически или по определению), то обратный элемент часто может быть как левым (), так и правым (). Эти два обратных элемента могут по отдельности существовать или не существовать, равняться или не равняться друг другу.
К примеру, отношение матриц определяется через обратную матрицу, при этом даже для квадратных матриц может быть:
- .
Отношение тензоров в общем случае не определено.
Деление многочленов[править | править код]
В общих чертах оно повторяет идеи деления натуральных чисел, ибо натуральное число есть не что иное, как значения многочлена, у которого коэффициенты — цифры, а вместо переменной стоит основание системы счисления:
- .
Поэтому аналогично определяются: частное, делитель, делимое и остаток (с той лишь разницей, что ограничение накладывается на степень остатка). Поэтому к делению многочленов также применимо деление столбиком.
Отличие же заключается в том, что при делении многочленов основной упор делается на степени делимого и делителя, а не на коэффициенты. Поэтому обычно считается, что частное и делитель (а следовательно и остаток) определены с точностью до постоянного множителя.
Деление на ноль[править | править код]
По определению числовых множеств деление на число 0 не определено. Частное от деления какого-либо отличного от нуля числа на ноль не существует, так как в этом случае никакое число не может удовлетворять определению частного[8]. Для определения данной ситуации полагают, что результат этой операции считается «бесконечно большим» или «равным бесконечности» (положительной или отрицательной, в зависимости от знака операндов).
С геометрической точки зрения выполняется аффинное расширение числовой прямой. То есть привычная последовательность вещественных чисел «сжимается» так, чтобы можно было оперировать границами этой последовательности. В качестве границ (условных) введены две абстрактные бесконечно большие величины .
С точки зрения общей топологии выполняется двухточечная компактификация числовой прямой путем добавления двух идеализированных точек (бесконечностей с противоположным знаком). Пишут:
Если произвести проективное расширение множества вещественных чисел введением идеализированной точки ,которая соединяет оба конца вещественной прямой, тогда с точки зрения общей топологии будет выполнена одноточечная компактификация числовой прямой путем добавления бесконечности без знака. Дополним полученное множество чисел новым элементом , в результате получится , на данной основе строится алгебраическая структура называемая «Колесом» (Wheel)[9]. Термин был взят из-за схожести с топологической картинкой проективного расширения числовой прямой и точки 0/0. Внесенные изменения превращают эту алгебраическую систему в моноид как по операции сложения (с нулем в качестве нейтрального элемента), так и по операции умножения (с единицей в качестве нейтрального элемента). Это тип алгебры, где деление всегда определено. В частности, деление на ноль имеет смысл.
Существуют и другие алгебраические системы с делением на ноль. Например, «общие луга» (common meadows)[10]. Они чуть проще, так как не расширяют пространство, вводя новые элементы. Цель достигается как в колесах, трансформацией операций сложения и умножения, а также отказом от бинарного деления.
См. также[править | править код]
- Признаки делимости
- Наибольший общий делитель
- Наименьшее общее кратное
- Деление многочленов столбиком
- Деление столбиком
- Остаток от деления
- Деление с остатком
Примечания[править | править код]
- ↑ Так эти свойства называются в учебниках для младших классов
- ↑ Системы счисления, 2006, p. 3.
- ↑ Поскольку на множестве вещественных чисел уже введено отношение линейного порядка, то мы можем определить топологию числовой прямой: в качестве открытых множеств возьмём всевозможные объединения интервалов вида
- ↑ Ильин, 1985, с. 46.
- ↑ Уравнение заменой переменных легко свести к уравнению гиперболического параболоида .
- ↑ Волинская Н. И. Интегрированный урок по физике и математике, Измерение физических величин и их единицы, СШ 7 г. Бреста. brestschool7.iatp.by. Дата обращения: 18 апреля 2016. Архивировано 7 августа 2016 года.
- ↑ Макаров Владимир Петрович. О «размерности» физических величин. lithology.ru, Литология.РФ. Дата обращения: 18 апреля 2016. Архивировано 6 мая 2016 года.
- ↑ М. Я. Выгодский Справочник по элементарной математике.
- ↑ Jesper Carlstrom. Wheels — On Division by Zero. — Stockholm: Department of Mathematics Stockholm University, 2001. — 48 с.
- ↑ Jan A. Bergstra and Alban Ponse. Division by Zero in Common Meadows. — The Netherlands: Section Theory of Computer Science Informatics Institute, Faculty of Science University of Amsterdam, 2014. — 16 с. Архивировано 26 марта 2018 года.
Литература[править | править код]
- Ильин В.А. и др. Математический анализ. Начальный курс. (неопр.). — МГУ, 1985. — Т. 1. — 662 с.
- Системы счисления. — Вологда: ГОУ СПО «Вологодский машиностроительный техникум», 2006. — С. 3. — 16 с.












































![{\displaystyle [C],[A],[B],[R]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ffa55b211a6ce8d9ca5e65a08959906e47a3930)
![{\displaystyle \quad [C]=[A]:[B]=[\rightarrow (A/B)]\quad \&\quad [R]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da53f8f946ffe1f91e6d1e7ff4753ba458b2f4e6)
![{\displaystyle \quad [C]=[A]:[B]=[A/(\rightarrow B)]\quad \&\quad [R]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f41f0cc34c33325170aca03f967e68ef1d6c0ba)

















![{\displaystyle \alpha =[a_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c222a30a9a92c2e3eef762e7c2c43dceb2bb4d8c)
![{\displaystyle \beta =[b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a26985ffa366493195dac10ceda47058558cd721)
![{\displaystyle \gamma =[c_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34668f3552cf8e843401e133627da1ff0651fa03)


![{\displaystyle \gamma =\alpha :\beta {\overset {\text{def}}{=}}[a_{n}]:[b_{n}]=[a_{n}/b_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c7c327b2023d43d9237f3c51232bae01b5ffb71)





























































